[人工智能]【计算机视觉与深度学习】全连接神经网络（二）

计算机视觉与深度学习系列博客传送门
【计算机视觉与深度学习】线性分类器（一）
【计算机视觉与深度学习】线性分类器（二）
【计算机视觉与深度学习】全连接神经网络（一）

激活函数再探讨

首先我们来看Sigmoid函数$$\sigma (x)=\frac{1}{1+e^{?x}}$$对其求导$${\sigma }^{\prime }(x)=\sigma (x)(1?\sigma (x))$$

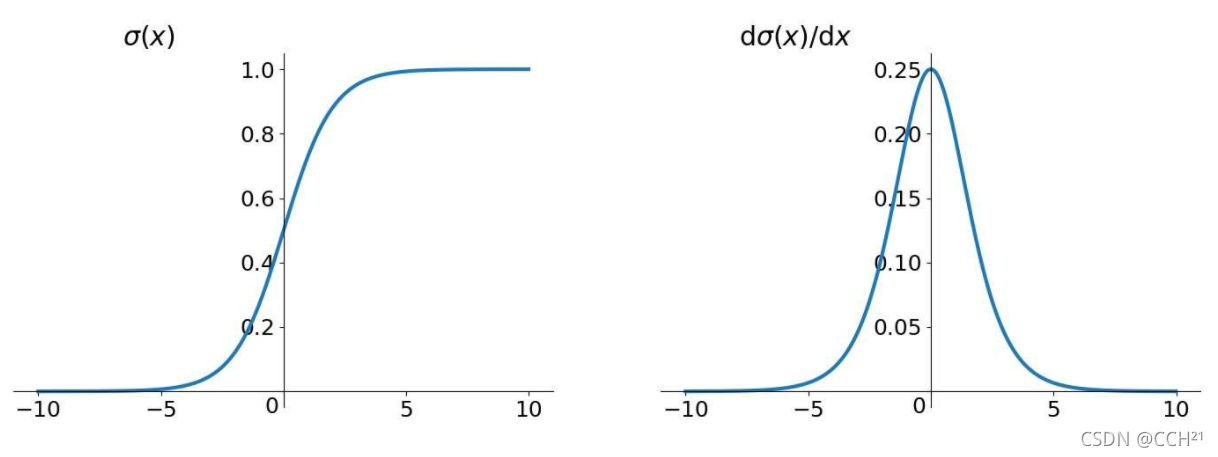
当输入值大于10或小于-10的时候，Sigmoid函数的局部梯度都接近0，这是非常不利于网络的梯度流传递的。这就是梯度消失问题，本质上，梯度消失是链式法则的乘法特性导致的。
与之相对应的是梯度爆炸。梯度爆炸也是链式法则的乘法特性导致的，函数“断崖处”的梯度乘上学习率后会是一个非常大的值，从而在更新参数时“飞”出了合理区域，最终会导致算法不收敛。

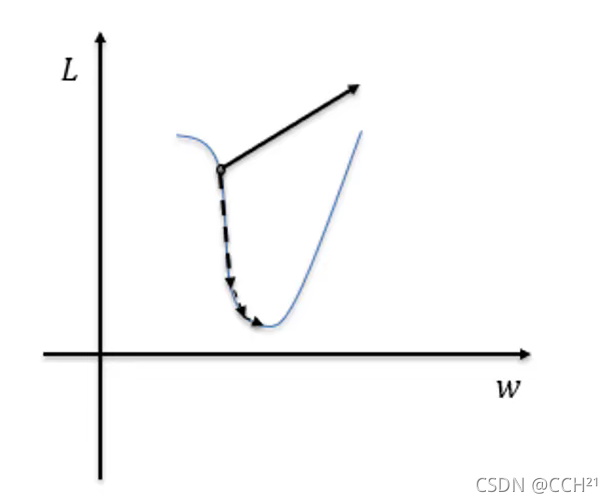
解决梯度爆炸的一个方案是使用梯度裁剪，把沿梯度方向前进的步长限制在某个值内就可以避免在更新参数时“飞”出合理区域。
我们再看双曲正切函数$$\tanh (x)=\frac{\sin hx}{\cos hx}=\frac{e^x?e^{?x}}{e^x+e^{?x}}$$对其求导$${\tanh }^{\prime }(x)=1?{\tanh }^2(x)$$

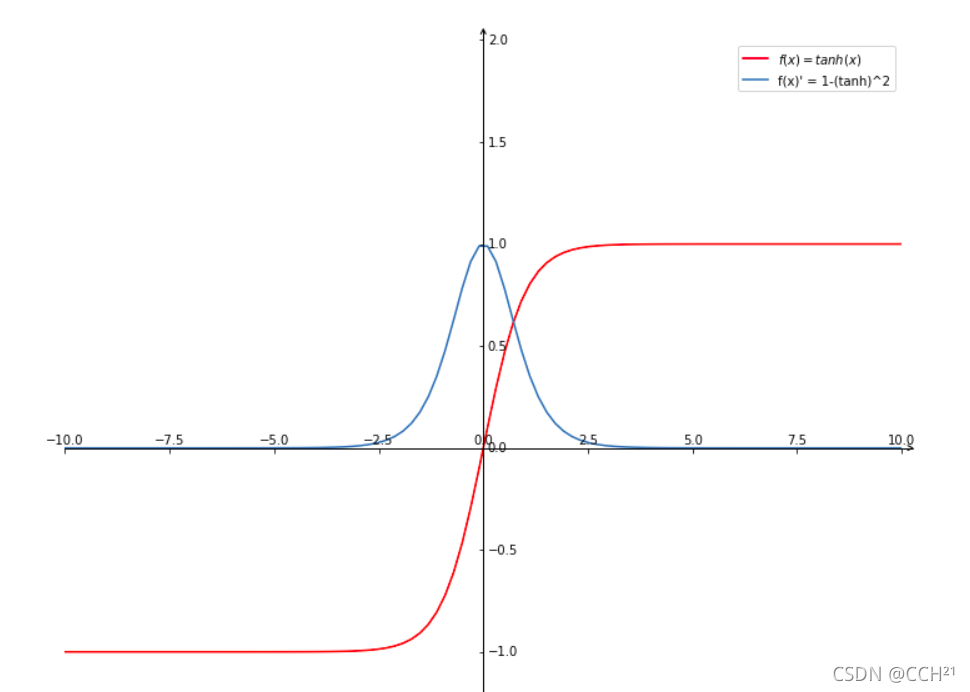
与Sigmoid函数类似，tanh函数的局部梯度特性不利于网络梯度流的反向传递。
接下来是ReLU函数$$ReLU(x)=\max (0,x)$$

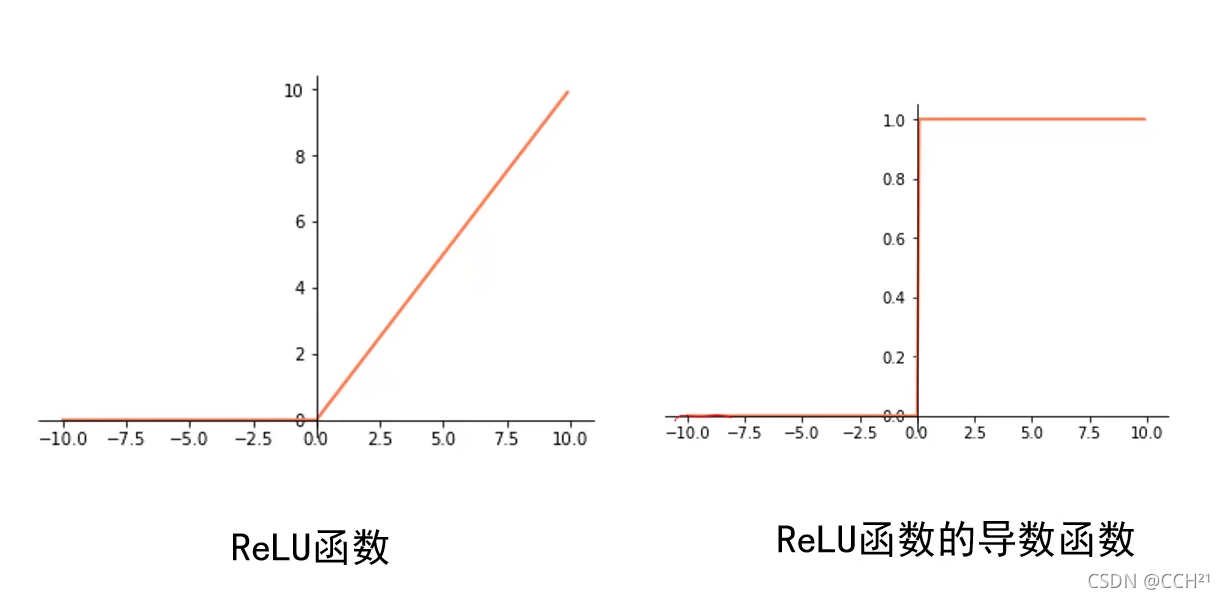
当输入大于0时，局部梯度永远不会为0，这比较有利于梯度流的传递。但ReLU函数仍有一些不完美，当输入小于等于0时（当输入为0时函数没有导数，一般规定0处的导数值为0），其导数值为0，因此提出了LeakyReLU函数$$LeakyReLU(x)=\max (\alpha x,x)$$

LeakyReLU函数基本没有“死区”，即梯度永远不会为0。之所以说“基本”，是因为函数在0处没有导数，前向计算中输入为0的概率非常小，几乎没有可能，所以函数在0处没有导数对于计算而言没有影响。
对于激活函数的选择，我们应当尽可能地选择ReLU函数或LeakyReLU函数，相比于Sigmoid函数和tanh函数，ReLU函数和LeakyReLU函数会让梯度流的传递更加顺畅，训练过程收敛得更快，也能更有效地防止梯度消失。

梯度下降算法的改进

梯度下降算法存在的问题

在全连接神经网络中，损失函数有一个特性，就是在一个方向上变化迅速，而在另一个方向上变化缓慢。当我们想要优化参数使得损失值更小的时候，若使用梯度下降法，损失值就会在“山壁”间震荡，而往“山谷”底端行进的速度较慢。若我们发现模型收敛速度过慢，只是简单地增大学习率（即步长）是不能加快收敛速度的。

动量法

改进梯度下降算法存在的问题，一个最简单的想法就是减少“山壁”间的震荡，加快前往“谷底”的速度，因此我们可以利用累加历史梯度信息来更新梯度，这就是动量法。
在小批量梯度下降算法上进行改进。在迭代前设置动量系数$\mu$，初始化速度$v=0$。此前的迭代过程中，更新权值是令$$\theta :=\theta ?\alpha g$$其中$\alpha$为学习率，$g$为计算出的梯度。使用动量法，每次迭代过程中，令速度更新为$$v:=\mu v+g$$再利用更新的速度更新权值$$\theta :=\theta ?\alpha v$$
对于动量系数$\mu$，其取值范围为$[0,1)$，当$\mu =0$时，动量法等价于梯度下降算法。一般我们设置$\mu =0.9$。
使用动量法的好处在于，历史梯度信息累加过程中，震荡方向相互抵消，而前往“谷底”的方向得到加强，进而加快了模型的收敛速度。
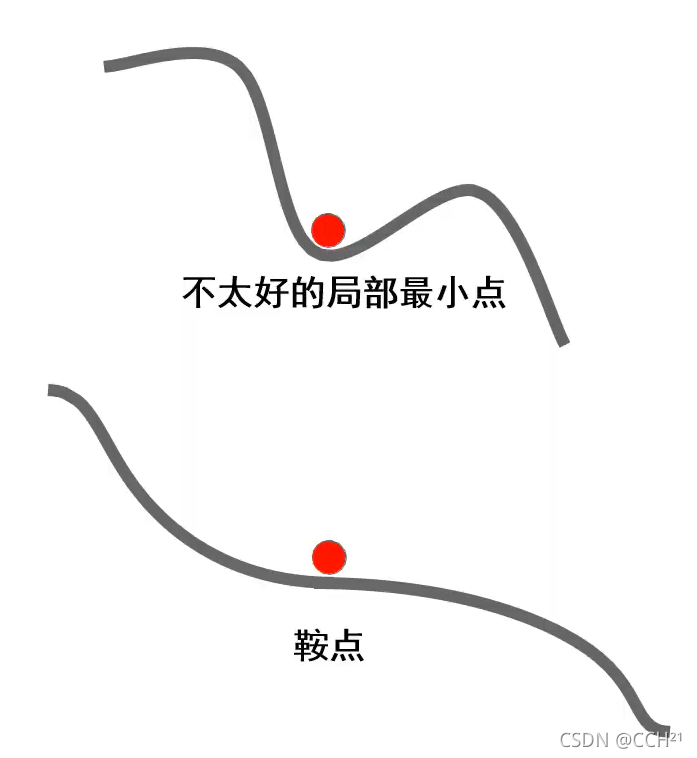
动量法还能解决一些常见现象带来的问题，例如损失函数常具有不太好的局部最小点或鞍点（高维空间非常常见），在这些点的位置上，梯度为0，若使用梯度下降算法更新参数会认为模型已经收敛，参数不会再更新。如果使用动量法，由于动量的存在，算法可以冲出局部最小点和鞍点，进而找到更优解。

自适应梯度法，AdaGrad算法与RMSProp算法

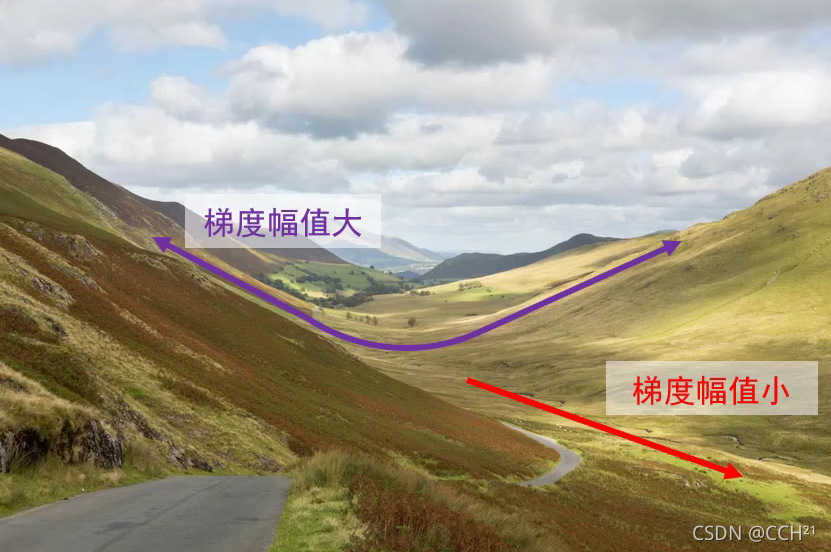
自适应梯度法与动量法的思路不同。梯度幅度平方较大的方向是震荡方向，梯度幅度平方较小的方向是平坦方向。自适应梯度法通过减小震荡方向步长、增大平坦方向步长的方法来减小震荡，加速通往“谷底”。
AdaGrad算法是一种自适应梯度算法，下面在小批量梯度下降算法上进行改进实现AdaGrad算法。
在迭代前设置小常数$\delta$（用于被小数除时的数值稳定，一般设置为$10^{?5}$），初始化累积变量$r=0$。在迭代过程中，计算出梯度$g$，累计平方梯度$$r:=r+g^2$$再利用累积平方梯度更新权值$$w:=w?\frac{\alpha }{\sqrt{r}+\delta }g$$其中$\alpha$为学习率。由于震荡方向的累积平方梯度较大，将其开根号后作为分母，计算得出的值就会是一个比较小的值。同理，平坦方向计算得出的值是一个比较大的值。这样就加快了模型收敛速度。
但是，AdaGrad算法也存在不足，随着累积时间的变长，累积变量$r$将会是一个非常大的值，此时更新参数的步长就会变得非常小，从而失去了调节作用。为了解决这一问题，RMSProp算法被提出。
RMSProp算法也是一种自适应梯度算法。在迭代前设置衰减速率$\rho$，小常数$\delta$（一般设置为$10^{?5}$），初始化累积变量$r=0$。与AdaGrad算法不同，RMSProp算法在迭代过程中累积平方梯度$$r:=\rho r+(1?\rho )g^2$$再利用累积平方梯度更新权值$$w:=w?\frac{\alpha }{\sqrt{r}+\delta }g$$其中$\alpha$为学习率。衰减速率$\rho$的取值范围为$[0,1)$，它削弱了历史梯度信息，一般设置$\rho =0.999$。

Adam算法

Adam算法是动量法和自适应梯度法的思想结合而成的产物。在迭代前设置衰减速率$\rho$（一般设置为$0.999$），动量系数$\mu$（一般设置为$0.9$），小常数$\delta$（一般设置为$10^{?5}$），初始化累积变量$r=0,v=0$。在迭代过程中，计算梯度$g$，累积梯度$$v:=\mu v+(1?\mu )g$$累积平方梯度$$r:=\rho r+(1?\rho )g^2$$修正偏差$$v=\frac{v}{1?{\mu }^t}$$ $$r=\frac{r}{1?{\rho }^t}$$更新权值$$\theta :=\theta ?\frac{\alpha }{\sqrt{r}+\delta }v$$修正偏差步骤可以极大缓解算法初期的冷启动问题。算法初期，计算出的梯度$g$比较小，如果不进行修正会减慢算法的收敛速度。

权值初始化

全零初始化

使用全零初始化，网络中不同的神经元有相同的输出，进行同样的参数更新，因此，这些神经元学习的参数都一样，本质上等价于一个神经元。

随机权值初始化

使用包含10个隐藏层（每个隐藏层包含500个神经元）和1个输出层的网络进行实验，使用双曲正切激活函数，权值分别采样自$\mathcal{N}(0,0.01)$和$\mathcal{N}(0,1)$的高斯分布，实验结果如下图所示。


实验表明，使用随机权值初始化并不能保证网络能够正常地被训练。

Xavier初始化

我们希望网络各层的激活值和局部梯度的方差在传播过程中尽量保持一致，以保证网络中正向和反向的数据流动。
一个神经元，其输入为$z_1,z_2,...,z_N$，这$N$个输入是独立同分布的；其权值为$w_1,w_2,...,w_N$，它们也是独立同分布的；$\mathbf{w}$和$\mathbf{z}$是独立的，其激活函数为$f$，则输出$\mathbf{y}$的表达式为$$\mathbf{y}=f({\mathbf{w}}_1{\mathbf{z}}_1+{\mathbf{w}}_2{\mathbf{z}}_2+...+{\mathbf{w}}_N{\mathbf{z}}_N)$$这就是Xavier初始化。
Xavier初始化的目标是使网络各层的激活值和局部梯度的方差在传播过程中尽量保持一致，即寻找$\mathbf{w}$的分布使得输出$y$与输入$\mathbf{z}$的方差一致。假设$f$为双曲正切函数，$w_1,w_2,...,w_N$独立同分布，$z_1,z_2,...,z_N$独立同分布，$\mathbf{w}$和$\mathbf{z}$独立且均值都为$0$，则有
$$\begin{array}{rl}Var(\mathbf{y})& =Var(\sum _{i=1}^N{w}_i{z}_i)\\ & =\sum _{i=1}^{N}Var(w_i{z}_i)\\ & =\sum _{i=1}^N[E(w_i){]}^{2}Var(z_i)+[E(z_i){]}^{2}Var(w_i)+Var(w_i)Var(z_i)\\ & =\sum _{i=1}^{N}Var(w_i)Var(z_i)\\ & =nVar(w_i)Var(z_i)\end{array}$$
$Var(\mathbf{w})=\frac{1}{N}$时，$\mathbf{y}$的方差与$\mathbf{z}$的方差一致。
使用包含10个隐藏层（每个隐藏层包含500个神经元）和1个输出层的网络进行实验，使用双曲正切激活函数，权值采样自$\mathcal{N}(0,1/N)$的高斯分布，其中$N$为输入，得到下面的实验结果。

改变激活函数为ReLU函数，得到下面的实验结果。

根据实验结果可知，Xavier初始化方法不太适合ReLU激活函数。

HE初始化 (MSRA)

HE初始化与Xavier初始化的不同在于权值采样自$\mathcal{N}(0,2/N)$的高斯分布，其中$N$为输入。使用包含10个隐藏层（每个隐藏层包含500个神经元）和1个输出层的网络进行实验，使用ReLU激活函数进行实验，结果如下。

总结

好的初始化方法可以防止前向传播过程中的信息消失，也可以解决反向传播过程中的梯度消失。当激活函数选择Sigmoid函数或tanh函数时，建议使用Xavier初始化方法；当激活函数选择ReLU函数或LeakyReLU函数时，建议使用HE初始化方法。