目录
一、基本介绍
1.1原理
主成分分析是最常用的线性降维方法,通过某种线性投影,将高维的数据映射到低维的空间,并期望在所投影的维度上数据的信息量最大(方差最大),以较少的数据维度去反映原数据的特性。
在机器学习的实际问题中,一般都会有几十个指标,高维数据离散度较大,不利于训练出较好的参数,而低维数据则可以更好的训练参数,因此可以通过降维的形式,计算出k列映射数据替代原数据。
1.2主成分分析的几何解释


通过旋转变换坐标轴使得n个样品点在F1轴方向上的离散程度最大,即F1的方差最大。变量F1代表了原始数据的绝大部分信息,在研究某经济问题时,即使不考虑变量F2也无损大局。经过上述旋转变换原始数据的大部分信息集中到F1轴上,对数据中包含的信息起到了浓缩作用。?
1.3主要步骤
1.?求样本均值
2.求样本协方差矩阵S
3.计算协方差矩阵的特征值和特征向量
4.将特征值排序
5.保留前N个最大的特征值对应的特征向量
6.将原始特征转换到上面得到的N个特征向量构建的新空间中
7.写出主成分的表达式
注:第五步和第六步,实现了特征压缩。?
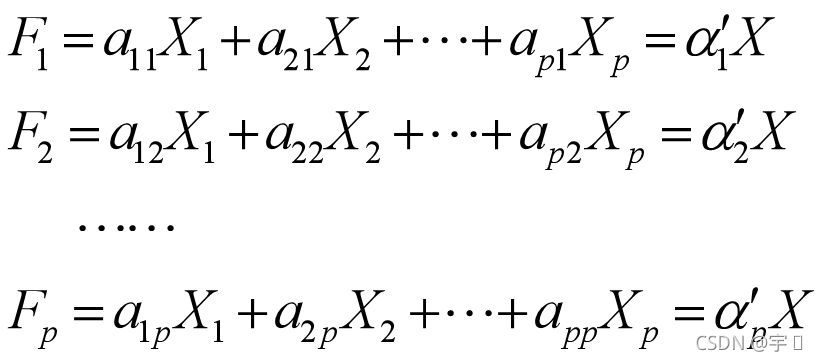
每个主成分的系数平方和为1。即
![]()
?主成分之间相互独立,即无重叠的信息。即
![]()
?主成分的方差依次递减,重要性依次递减,即
![]()
1.4主成分个数的选取原则
首先需要计算各主成分的方差,再求出各自对应的方差贡献率(即对应主成分方差除以总方差),?根据累积贡献率的大小取前面m 个(m<p)主成分,p代表所有的主成分。
选取原则:?????
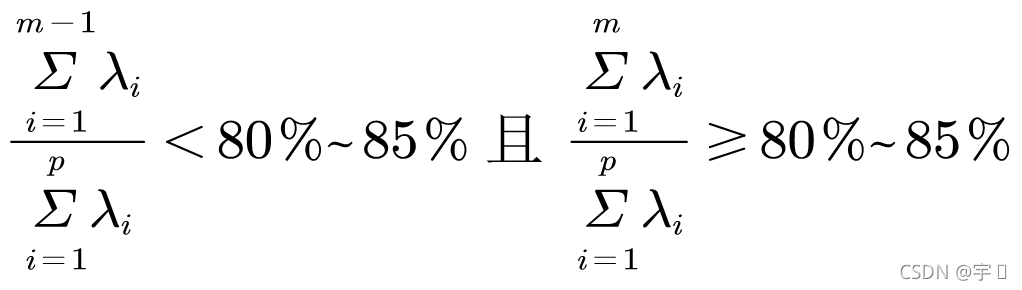
?二、主成分分析代码
2.1MATLAB代码
clear;clc
PHO = [1 0.79 0.36 0.76 0.25 0.51
0.79 1 0.31 0.55 0.17 0.35
0.36 0.31 1 0.35 0.64 0.58
0.76 0.55 0.35 1 0.16 0.38
0.25 0.17 0.64 0.16 1 0.63
0.51 0.35 0.58 0.38 0.63 1];
[COEFF,latent,explained] = pcacov(PHO)
%分别代表协方差矩阵、特征值、贡献率
% 为了更加直观,以元胞数组形式显示结果
result1(1,:) = {'特征值', '差值', '贡献率', '累积贡献率'};
result1(2:7,1) = num2cell(latent);
result1(2:6,2) = num2cell(-diff(latent));
result1(2:7,3:4) = num2cell([explained, cumsum(explained)])
% 以元胞数组形式显示主成分表达式
s = {'标准化变量';'x1:身高';'x2:坐高';'x3:胸围';'x4:手臂长';'x5:肋围';'x6:腰围'};
result2(:,1) = s ;
result2(1, 2:4) = {'Prin1', 'Prin2', 'Prin3'};
result2(2:7, 2:4) = num2cell(COEFF(:,1:3))
?2.2Python代码
from sklearn.decomposition import PCA
import pandas as pd
import os
path=".csv"#存放文件路径
df=pd.read_csv(path)#读取文件
pca=PCA()#创建对象
df=(df.iloc[:,2:]-df.iloc[:,2:].mean())/df.iloc[:,2:].std()#对数据进行中心化处理
#print(df)
pca.fit(df)
print(pca.components_)#返回模型的各个特征向量
print(pca.explained_variance_ratio_)#返回各个成分各自的方差百分比
pca=PCA(2)#设置转化主成分个数两个
pca.fit(df)
low_d=pca.transform(df)
print(low_d)#返回降维后的数据
?三、实用案例
下表列出了2007年我国31个省、市、自治州和直辖市的农村居民家庭平均每人全年消费性支出的8个主要变量数据。是根据这8个主要变量的观测数据,进行主成分分析。?
| 单位:元 | |||||||
| 地区 | 食??品 | 衣??着 | 居??住 | 家庭设备 及服务 | 交通和通讯 | 文教娱乐 用品及服务 | 医疗保健 |
| ?北??京 | 2132.51 | 513.44 | 1023.21 | 340.15 | 778.52 | 870.12 | 629.56 |
| ?天??津 | 1367.75 | 286.33 | 674.81 | 126.74 | 400.11 | 312.07 | 306.19 |
| ?河??北 | 1025.72 | 185.68 | 627.98 | 140.45 | 318.19 | 243.30 | 188.06 |
| ?山??西 | 1033.68 | 260.88 | 392.78 | 120.86 | 268.75 | 370.97 | 170.85 |
| ?内蒙古 | 1280.05 | 228.40 | 473.98 | 117.64 | 375.58 | 423.75 | 281.46 |
| ?辽??宁 | 1334.18 | 281.19 | 513.11 | 142.07 | 361.77 | 362.78 | 265.01 |
| ?吉??林 | 1240.93 | 227.96 | 399.11 | 120.95 | 337.46 | 339.77 | 311.37 |
| ?黑龙江 | 1077.34 | 254.01 | 691.02 | 104.99 | 335.28 | 312.32 | 272.49 |
| ?上??海 | 3259.48 | 475.51 | 2097.21 | 451.40 | 883.71 | 857.47 | 571.06 |
| ?江??苏 | 1968.88 | 251.29 | 752.73 | 228.51 | 543.97 | 642.52 | 263.85 |
| ?浙??江 | 2430.60 | 405.32 | 1498.50 | 338.80 | 782.98 | 750.69 | 452.44 |
| ?安??徽 | 1192.57 | 166.31 | 479.46 | 144.23 | 258.29 | 283.17 | 177.04 |
| ?福??建 | 1870.32 | 235.61 | 660.55 | 184.21 | 465.40 | 356.26 | 174.12 |
| ?江??西 | 1492.02 | 147.71 | 474.49 | 121.54 | 277.15 | 252.78 | 167.71 |
| ?山??东 | 1369.20 | 224.18 | 682.13 | 195.99 | 422.36 | 424.89 | 230.84 |
| ?河??南 | 1017.43 | 189.71 | 615.62 | 136.37 | 269.46 | 212.36 | 173.19 |
| ?湖??北 | 1479.04 | 168.64 | 434.91 | 166.25 | 281.12 | 284.13 | 178.77 |
| ?湖??南 | 1675.16 | 161.79 | 508.33 | 152.60 | 278.78 | 293.89 | 219.95 |
| ?广??东 | 2087.58 | 162.33 | 763.01 | 163.85 | 443.24 | 254.94 | 199.31 |
| ?广??西 | 1378.78 | 86.90 | 554.14 | 112.24 | 245.97 | 172.45 | 149.01 |
| ?海??南 | 1430.31 | 86.26 | 305.90 | 93.26 | 248.08 | 223.98 | 95.55 |
| ?重??庆 | 1376.00 | 136.34 | 263.73 | 138.34 | 208.69 | 195.97 | 168.57 |
| ?四??川 | 1435.52 | 156.65 | 366.45 | 142.64 | 241.49 | 177.19 | 174.75 |
| ?贵??州 | 998.39 | 99.44 | 329.64 | 70.93 | 154.52 | 147.31 | 79.31 |
| ?云??南 | 1226.69 | 112.52 | 586.07 | 107.15 | 216.67 | 181.73 | 167.92 |
| ?西??藏 | 1079.83 | 245.00 | 418.83 | 133.26 | 156.57 | 65.39 | 50.00 |
| ?陕??西 | 941.81 | 161.08 | 512.40 | 106.80 | 254.74 | 304.54 | 222.51 |
| ?甘??肃 | 944.14 | 112.20 | 295.23 | 91.40 | 186.17 | 208.90 | 149.82 |
| ?青??海 | 1069.04 | 191.80 | 359.74 | 122.17 | 292.10 | 135.13 | 229.28 |
| ?宁??夏 | 1019.35 | 184.26 | 450.55 | 109.27 | 265.76 | 192.00 | 239.40 |
| ?新??疆 | 939.03 | 218.18 | 445.02 | 91.45 | 234.70 | 166.27 | 210.69 |
clear;clc
[X,textdata] = xlsread('examp12_4_1.xls');
XZ = zscore(X);
% 调用princomp函数根据标准化后原始样本观测数据作主成分分析
[COEFF,SCORE,latent,tsquare] = pca(XZ)
% 为了直观,定义元胞数组result1,用来存放特征值、贡献率和累积贡献率等数据
explained = 100*latent/sum(latent);
[m, n] = size(X);
result1 = cell(n+1, 4);
result1(1,:) = {'特征值', '差值', '贡献率', '累积贡献率'};
result1(2:end,1) = num2cell(latent);
result1(2:end-1,2) = num2cell(-diff(latent));
result1(2:end,3:4) = num2cell([explained, cumsum(explained)])
% 为了直观,定义元胞数组result2,用来存放前2个主成分表达式的系数数据
varname = textdata(3,2:end)';
result2 = cell(n+1, 3);
result2(1,:) = {'标准化变量', '主成分Prin1', '主成分Prin2'};
result2(2:end, 1) = varname;
result2(2:end, 2:end) = num2cell(COEFF(:,1:2))
% 为了直观,定义元胞数组result3,用来存放每一个地区总的消费性支出,以及前2个主成分的得分数据
cityname = textdata(4:end,1);
sumXZ = sum(XZ,2);
[s1, id] = sortrows(SCORE,1);
result3 = cell(m+1, 4);
result3(1,:) = {'地区', '总支出', '第一主成分得分y1', '第二主成分得分y2'};
result3(2:end, 1) = cityname(id);
result3(2:end, 2:end) = num2cell([sumXZ(id), s1(:,1:2)])
% 为了直观,定义元胞数组result4,用来存放前2个主成分的得分数据,以及(食品+其他)-(衣着+医疗)
cloth = sum(XZ(:,[1,8]),2) - sum(XZ(:,[2,7]),2);
[s2, id] = sortrows(SCORE,2);
result4 = cell(m+1, 4);
result4(1,:) = {'地区','第一主成分得分y1','第二主成分得分y2' ,'(食+其他)-(衣+医)'};
result4(2:end, 1) = cityname(id);
result4(2:end, 2:end) = num2cell([s2(:,1:2), cloth(id)])
%***************************前两个主成分得分散点图***************************
for i = 1:length(X)
plot(SCORE(i,1),SCORE(i,2),'ko');
text(SCORE(i,1)+0.02,SCORE(i,2)+0.05,cityname{i},'FontSize',10,'fontname','宋体');
hold on
end
xlabel('第一主成分得分');
ylabel('第二主成分得分');
set(gca,'FontName','宋体');
result5 = sortrows([cityname, num2cell(tsquare)],2);
[{'地区', '霍特林T^2统计量'}; result5]