开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 人工智能 -> 机器学习线性回归 -> 正文阅读

[人工智能]机器学习线性回归

2.1 线性回归简介

学习目标

了解线性回归的应用场景
知道线性回归的定义

1 线性回归应用场景

房价预测
销售额预测
贷款额度预测

线性关系举例：

2 什么是线性回归

2.1 定义与公式

线性回归(Linear regression)是利用回归方程(函数)对一个或多个自变量(特征值)和因变量(目标值)之间关系进行建模的一种分析方式。

特点：只有一个自变量的情况称为单变量回归，多于一个自变量情况的叫做多元回归。

通用公式 $h(w)=w{_1}x{_1}+w{_2}x{_2}+w{_3}x{_3}+...+b=w^Tx+b$ ,

其中 $w$ , $x$ 可以理解为矩阵： $\begin{pmatrix} b \\ w{_1} \\ w{_2} \\ \vdots \end{pmatrix}$ , $\begin{pmatrix} 1 \\ x{_1} \\ x{_2}\\\vdots \end{pmatrix}$
线性回归用矩阵表示举例
$\begin{cases}1 \times x{_1} + x{_2} = 2 \\ 0 \times x{_1} + x{_2} = 2 \\ 2 \times x{_1} + x{_2} = 3 \end{cases}$

? 写成矩阵形式：
$KaTeX parse error: No such environment: split at position 8: \begin{?s?p?l?i?t?}? &\begin{bmat…$
? 从列的角度看：
$KaTeX parse error: No such environment: split at position 8: \begin{?s?p?l?i?t?}? &\begin{bmatri…$

那么怎么理解呢？我们来看几个例子

期末成绩：0.7×考试成绩+0.3×平时成绩
房子价格 = 0.02×中心区域的距离 + 0.04×城市一氧化氮浓度 + (-0.12×自住房平均房价) + 0.254×城镇犯罪率

上面两个例子，我们看到特征值与目标值之间建立了一个关系，这个关系可以理解为线性模型。

2.2 线性回归的特征与目标的关系分析

线性回归当中主要有两种模型，**一种是线性关系，另一种是非线性关系。**在这里我们只能画一个平面更好去理解，所以都用单个特征或两个特征举例子。

线性关系
- 单变量线性关系：
- 多变量线性关系
  
  注释：单特征与目标值的关系呈直线关系，或者两个特征与目标值呈现平面的关系

更高维度的我们不用自己去想，记住这种关系即可

非线性关系

注释：为什么会这样的关系呢？原因是什么？

如果是非线性关系，那么回归方程可以理解为：

$w_1x_1+w_2x_2^2+w_3x_3^2$

小结

线性回归的定义【了解】
- 利用回归方程(函数)对一个或多个自变量(特征值)和因变量(目标值)之间关系进行建模的一种分析方式
线性回归的分类【知道】
- 线性关系
- 非线性关系

2.2 线性回归api初步使用

学习目标

知道线性回归api的简单使用

1 线性回归API

sklearn.linear_model.LinearRegression()
- LinearRegression.coef_：回归系数
- LinearRegression.intercept_: 截距

2 举例

2.1 步骤分析

1.获取数据集
2.数据基本处理（该案例中省略）
3.特征工程（该案例中省略）
4.机器学习
5.模型评估（该案例中省略）

2.2 代码过程

导入模块

from sklearn.linear_model import LinearRegression

构造数据集

x = [[80, 86],
[82, 80],
[85, 78],
[90, 90],
[86, 82],
[82, 90],
[78, 80],
[92, 94]]
y = [84.2, 80.6, 80.1, 90, 83.2, 87.6, 79.4, 93.4]

机器学习-- 模型训练

# 实例化API
estimator = LinearRegression()

# 使用fit方法进行训练,得到模型
estimator.fit(x,y)

# 打印回归系数(每个特征列前的系数)
estimator.coef_

# 打印截距
estimator.intercept_

# 利用训练的模型进行预测
estimator.predict([[100, 80]])

小结

sklearn.linear_model.LinearRegression()
- LinearRegression.coef_：回归系数
- LinearRegression.intercept_: 截距

2.3 数学:求导

学习目标

知道常见的求导方法
知道导数的四则运算

1 导数的概念回顾

导数（Derivative），也叫导函数值。又名微商，是微积分中的重要基础概念。
- 当函数y=f（x）的自变量x在一点x0上产生一个增量Δx时，函数输出值的增量Δy与自变量增量Δx的比值在Δx趋于0时的极限a如果存在，a即为在x0处的导数，记作f’（x0）或df（x0）/dx。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-9LNIMY0r-1631190399726)(./images/导数.jpeg)]
导数是函数的局部性质。一个函数在某一点的导数描述了这个函数在这一点附近的变化率。
- 如果函数的自变量和取值都是实数的话，函数在某一点的导数就是该函数所代表的曲线在这一点上的切线斜率
- 导数的本质是通过极限的概念对函数进行局部的线性逼近。例如在运动学中，物体的位移对于时间的导数就是物体的瞬时速度
不是所有的函数都有导数，一个函数也不一定在所有的点上都有导数。
- 若某函数在某一点导数存在，则称其在这一点可导，否则称为不可导
- 可导的函数一定连续；不连续的函数一定不可导
对于可导的函数f(x)，x?f’(x)也是一个函数，称作f(x)的导函数（简称导数）。寻找已知的函数在某点的导数或其导函数的过程称为求导
- 实质上，求导就是一个求极限的过程，导数的四则运算法则也来源于极限的四则运算法则
- 已知导函数也可以倒过来求原来的函数

2 常见函数的导数

公式	例子
$(C)^\prime=0$	$\left(5\right)^\prime=0$ $\left(10\right)^\prime=0$
$\left(x^\alpha\right)^\prime=\alpha x^{\alpha-1}$	$\left(x^3\right)^\prime=3 x^{2}$ $\left(x^5\right)^\prime=5 x^{4}$
$\left(a^x\right)^\prime=a^{x}\ln{a}$	$\left(2^x\right)^\prime=2^x\ln{2}$ $\left(7^x\right)^\prime=7^x\ln{7}$
$\left(e^x\right)^\prime=e^{x}$	$\left(e^x\right)^\prime=e^{x}$
$\left(\log{_a}x\right)^\prime=\frac{1}{x\ln{a}}$	$\left(\log{_{10}}x\right)^\prime=\frac{1}{x\ln{10}}$ $\left(\log{_{6}}x\right)^\prime=\frac{1}{x\ln{6}}$
$\left(\ln{x}\right)^\prime=\frac{1}{x}$	$\left(\ln{x}\right)^\prime=\frac{1}{x}$
$\left(\sin{x}\right)^\prime=\cos{x}$	$\left(\sin{x}\right)^\prime=\cos{x}$
$\left(\cos{x}\right)^\prime=-\sin{x}$	$\left(\cos{x}\right)^\prime=-\sin{x}$

3 导数的四则运算

公式	例子
$\left[u(x)\pm v(x)\right]^\prime=u^\prime(x) \pm v^\prime(x)$	$(e^x+4\ln{x})^\prime=(e^x)^\prime+(4\ln{x})^\prime=e^x+\frac{4}{x}$
$\left[u(x)\cdot v(x)\right]^\prime=u^\prime(x) \cdot v(x) + u(x) \cdot v^\prime(x)$	$(\sin{x}\cdot\ln{x})^\prime=\cos{x}\cdot\ln{x}+\sin{x}\cdot\frac{1}{x}$
$\left[\frac{u(x)}{v(x)}\right]^\prime=\frac{u^\prime(x) \cdot v(x) - u(x) \cdot v^\prime(x)}{v^2(x)}$	$\left(\frac{e^x}{\cos{x}}\right)^\prime=\frac{e^x\cdot\cos{x}-e^x\cdot(-\sin{x})}{cos^2(x)}$
$\{g[h(x)]\}^\prime=g^\prime(h)*h^\prime(x)$	$(\sin{2x})^\prime=\cos{2x}\cdot(2x)^\prime=2\cos(2x)$

4 练习

$y = x^3-2x^2+sinx$ ,求 $f^\prime(x)$
$(e^x+4lnx)^\prime$
$(sinx*lnx)^\prime$
$(\frac{e^x}{cosx})^\prime$
$y=\sin2x$ , 求 $\frac{dy}{dx}$
$(e^{2x})^\prime$

答案：

$y^\prime=(x^3-2x^2+\sin{x})^\prime=(x^3)^\prime-(2x^2)^\prime+(\sin{x})^\prime = 3x^2-4x+\cos{x}$
$(e^x+4lnx)^\prime=(e^x)^\prime+(4\ln{x})^\prime=e^x+\frac{4}{x}$
$(sinx*lnx)^\prime=(\sin{x})^\prime\cdot\ln{x}+\sin{x}\cdot(\ln{x})^\prime=\cos{x}\cdot\ln{x}+\sin{x}\cdot\frac{1}{x}$
$\left(\frac{e^x}{\cos{x}}\right)^\prime=\frac{(e^x)^\prime\cdot\cos{x}-e^x\cdot(\cos{x})\prime}{\cos^2{x}}=\frac{e^x\cdot\cos{x}-e^x\cdot(-\sin{x})}{\cos^2(x)}$
$(\sin{2x})^\prime=\cos{2x}\cdot(2x)^\prime=2\cos(2x)$
$(e^{2x})^\prime=e^{2x}\cdot(2x)^\prime=2e^{2x}$

小结

常见函数的求导方式和导数的四则运算

2.4 线性回归的损失和优化

学习目标

知道线性回归中损失函数
知道使用正规方程对损失函数优化的过程
知道使用梯度下降法对损失函数优化的过程

如何确定回归方程

算法训练出来的回归方程，是否会满足所有的样本？
- 允许误差存在
- 目标，回归方程的结果与实际值的误差最小

既然存在误差，如何衡量误差？

1 损失函数

总损失定义为：
$\begin{aligned}J(w)&=(h(x_{1})-y_{1})^2+(h(x_{2})-y_{2})^2+...+(h(x_{m})-y_{m})^2 \\ &=\sum_{i=1}^m(h(x_{i})-y_{i})^2\end{aligned}$

$y_{i}$ 为第 $i$ 个训练样本的真实值
$h(x_{i})$ 为第 $i$ 个训练样本特征值组合预测函数,也称为目标函数
- 目标函数(objective function)是指所关心的目标(某一变量)与相关的因素(某些变量)的函数关系。简单的说，就是你求解后所得出的那个函数。
又称最小二乘法

如何去减少这个损失，使我们预测的更加准确些？既然存在了这个损失，我们一直说机器学习有自动学习的功能，在线性回归这里更是能够体现。这里可以通过一些优化方法去优化（其实是数学当中的求导功能）回归的总损失！！！

2 优化算法

如何去求模型当中的W，使得损失最小？（目的是找到最小损失对应的W值）

线性回归经常使用的两种优化算法
- 正规方程
- 梯度下降法

2.1 正规方程

2.1.1 什么是正规方程

$w=(X^TX)^{-1}X^Ty$

理解：X为特征值矩阵，y为目标值矩阵。直接求到最好的结果

缺点：当特征过多过复杂时，求解速度太慢并且得不到结果

2.1.2 正规方程求解举例

以下表示数据为例：

即：

运用正规方程方法求解参数：

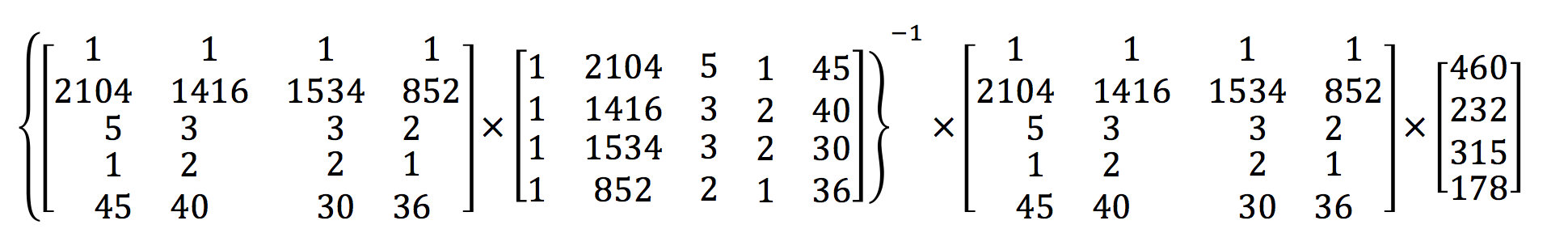
2.2 梯度下降(Gradient Descent)

2.2.1 什么是梯度下降

梯度下降法的基本思想可以类比为一个下山的过程。

假设这样一个场景：

一个人被困在山上，需要从山上下来(i.e. 找到山的最低点，也就是山谷)。但此时山上的浓雾很大，导致可视度很低。

因此，下山的路径就无法确定，他必须利用自己周围的信息去找到下山的路径。这个时候，他就可以利用梯度下降算法来帮助自己下山。

具体来说就是，以他当前的所处的位置为基准，寻找这个位置最陡峭的地方，然后朝着山的高度下降的地方走，（同理，如果我们的目标是上山，也就是爬到山顶，那么此时应该是朝着最陡峭的方向往上走）。然后每走一段距离，都反复采用同一个方法，最后就能成功的抵达山谷。

梯度下降的基本过程就和下山的场景很类似。

首先，我们有一个可微分的函数。这个函数就代表着一座山。

我们的目标就是找到这个函数的最小值，也就是山底。

根据之前的场景假设，最快的下山的方式就是找到当前位置最陡峭的方向，然后沿着此方向向下走，对应到函数中，就是找到给定点的梯度 ，然后朝着梯度相反的方向，就能让函数值下降的最快！因为梯度的方向就是函数值变化最快的方向。
所以，我们重复利用这个方法，反复求取梯度，最后就能到达局部的最小值，这就类似于我们下山的过程。而求取梯度就确定了最陡峭的方向，也就是场景中测量方向的手段。

2.2.2 梯度的概念

梯度是微积分中一个很重要的概念

在单变量的函数中，梯度其实就是函数的微分，代表着函数在某个给定点的切线的斜率；
在多变量函数中，梯度是一个向量，向量有方向，梯度的方向就指出了函数在给定点的上升最快的方向；
- 在微积分里面，对多元函数的参数求?偏导数，把求得的各个参数的偏导数以向量的形式写出来，就是梯度。

这也就说明了为什么我们需要千方百计的求取梯度！我们需要到达山底，就需要在每一步观测到此时最陡峭的地方，梯度就恰巧告诉了我们这个方向。梯度的方向是函数在给定点上升最快的方向，那么梯度的反方向就是函数在给定点下降最快的方向，这正是我们所需要的。所以我们只要沿着梯度的反方向一直走，就能走到局部的最低点！

2.2.3 梯度下降举例

1. 单变量函数的梯度下降

我们假设有一个单变量的函数 : $J(\theta) = \theta^2$

函数的微分： $J^\prime(\theta) = 2\theta$

初始化，起点为(已知的起始位置)： $\theta^0 = 1$

学习率(步长)： $\alpha = 0.4$

我们开始进行梯度下降的迭代计算过程:
$KaTeX parse error: No such environment: eqnarray at position 15: \large \begin{?e?q?n?a?r?r?a?y?}? \theta^0 &=& 1…$

如图，经过四次的运算，也就是走了四步，基本就抵达了函数的最低点，也就是山底

2.多变量函数的梯度下降

我们假设有一个目标函数： $J(\theta) = \theta_{1}^{2} + \theta_{2}^{2}$

现在要通过梯度下降法计算这个函数的最小值。我们通过观察就能发现最小值其实就是 (0，0)点。但是接下
来，我们会从梯度下降算法开始一步步计算到这个最小值!
我们假设初始的起点为： $\theta^{0} = (1, 3)$

初始的学习率(步长)： $\alpha = 0.1$

函数的梯度为： $\Delta J(\theta) =< 2\theta_{1} ,2\theta_{2}>$

进行多次迭代：
$$
\begin{eqnarray}
\Theta^0 &=& (1, 3) \
\Theta^1 &=& \Theta^0-\alpha\Delta J(\Theta)\
&=&(1,3)-0.1(2,6)\
&=&(0.8, 2.4)\
\Theta^2 &=& (0.8, 2.4)-0.1(1.6, 4.8)\
&=&(0.64, 1.92)\
\Theta^3 &=& (0.512, 1.536)\
\Theta^4 &=& (0.4096, 1.2288)\
\vdots\
\Theta^{10} &=& (0.10737418240000003, 0.32212254720000005)\
\vdots\
\Theta^{50} &=& (1.1417981541647683e^{-5}, 3.425394462494306e^{-5})\
\vdots\
\Theta^{100} &=& (1.6296287810675902e^{-10}, 4.888886343202771e^{-10})\

\end{eqnarray}
$$

我们发现，已经基本靠近函数的最小值点

2.2.4 梯度下降（Gradient Descent）公式

$\Large \theta_{i+1} = \theta_{i} - \alpha\frac{\partial}{\partial\theta_{i}}J(\theta)$

1) $\alpha$ 是什么含义？

$\alpha$ 在梯度下降算法中被称作为学习率或者步长，意味着我们可以通过α来控制每一步走的距离，控制参数不要走太快，错过了使损失函数取最小值的点。同时也要保证不要走的太慢，导致太阳下山了，还没有走到山下。所以α的选择在梯度下降法中往往是很重要的！α不能太大也不能太小，太小的话，可能导致迟迟走不到最低点，太大的话，会导致错过最低点！

2) 为什么梯度要乘以一个负号？

梯度前加一个负号，就意味着朝着梯度相反的方向前进！我们在前文提到，梯度的方向实际就是函数在此点上升最快的方向！而我们需要朝着下降最快的方向走，自然就是负的梯度的方向，所以此处需要加上负号

我们通过两个图更好理解梯度下降的过程

所以有了梯度下降这样一个优化算法，回归就有了"自动学习"的能力

优化动态图演示

3 梯度下降和正规方程的对比

3.1 两种方法对比

梯度下降	正规方程
需要选择学习率	不需要
需要迭代求解	一次运算得出
特征数量较大(超过10000个)可以使用	需要计算方程，时间复杂度高O(n3)

经过前面的介绍，我们发现最小二乘法适用简洁高效，比梯度下降这样的迭代法似乎方便很多。但是这里我们就聊聊最小二乘法的局限性。

首先，最小二乘法需要计算 $X^TX$ 的逆矩阵，有可能它的逆矩阵不存在，这样就没有办法直接用最小二乘法了。
- 此时就需要使用梯度下降法。当然，我们可以通过对样本数据进行整理，去掉冗余特征。让 $X^TX$ 的行列式不为0，然后继续使用最小二乘法。
第二，当样本特征n非常的大的时候，计算 $X^TX$ 的逆矩阵是一个非常耗时的工作（nxn的矩阵求逆），甚至不可行。
- 此时以梯度下降为代表的迭代法仍然可以使用。
- 那这个n到底多大就不适合最小二乘法呢？如果你没有很多的分布式大数据计算资源，建议超过10000个特征就用迭代法吧。或者通过主成分分析降低特征的维度后再用最小二乘法。
第三，如果拟合函数不是线性的，这时无法使用最小二乘法，需要通过一些技巧转化为线性才能使用，此时梯度下降仍然可以用。
第四，以下特殊情况：
- 当样本量m很少，小于特征数n的时候，这时拟合方程是欠定的，常用的优化方法都无法去拟合数据。
- 当样本量m等于特征数n的时候，用方程组求解就可以了。
- 当m大于n时，拟合方程是超定的，也就是我们常用与最小二乘法的场景了。

3.2 算法选择依据：

小规模数据：
- 正规方程：LinearRegression
- 岭回归: Ridge
大规模数据：
- 梯度下降法：SGDRegressor

小结

损失函数【知道】
- 最小二乘法
线性回归优化方法【知道】
- 正规方程
- 梯度下降法
正规方程 – 一蹴而就【知道】
- 只是适合样本和特征比较少的情况
梯度下降法 – 循序渐进【知道】
- 梯度的概念
  - 单变量 – 切线
  - 多变量 – 向量
- 梯度下降法中关注的两个参数
  - α – 就是步长
    - 步长太小 – 下山太慢
    - 步长太大 – 容易跳过极小值点
  - 为什么梯度要加一个负号
    - 梯度方向是上升最快方向,负号就是下降最快方向
梯度下降法和正规方程选择依据【知道】
- 小规模数据：
  - 正规方程：LinearRegression
  - 岭回归: Ridge
- 大规模数据：
  - 梯度下降法：SGDRegressor

2.5 梯度下降方法介绍

学习目标

了解全梯度下降算法的原理
了解随机梯度下降算法的原理
了解随机平均梯度下降算法的原理
了解小批量梯度下降算法的原理

1 梯度下降法大家族

首先，我们来看一下，常见的梯度下降算法有：

全梯度下降算法(Full gradient descent),
随机梯度下降算法(Stochastic gradient descent),
小批量梯度下降算法(Mini-batch gradient descent),
随机平均梯度下降算法(Stochastic average gradient descent)

它们都是为了正确地调节权重向量，通过为每个权重计算一个梯度，从而更新权值，使目标函数尽可能最小化。其差别在于样本的使用方式不同。

1.1 全梯度下降算法(FG)

批量梯度下降法，是梯度下降法最常用的形式，具体做法也就是在更新参数时使用所有的样本来进行更新。

计算训练集所有样本误差，对其求和再取平均值作为目标函数。

权重向量沿其梯度相反的方向移动，从而使当前目标函数减少得最多。

其是在整个训练数据集上计算损失函数关于参数 $\theta$ 的梯度：
$\large \theta_{i+1} = \theta_i - \alpha\sum_{j=0}^{m}(h_{\theta}(x_0^{(j)},x_1^{(j)},\cdots,x_n^{(j)})-y_j)x_i^{(j)}$

由于我们有m个样本，这里求梯度的时候就用了所有m个样本的梯度数据。

注意：

因为在执行每次更新时，我们需要在整个数据集上计算所有的梯度，所以批梯度下降法的速度会很慢，同时，全梯度下降法无法处理超出内存容量限制的数据集。
全梯度下降法同样也不能在线更新模型，即在运行的过程中，不能增加新的样本。

1.2 随机梯度下降算法(SG)

由于FG每迭代更新一次权重都需要计算所有样本误差，而实际问题中经常有上亿的训练样本，故效率偏低，且容易陷入局部最优解，因此提出了随机梯度下降算法。

其每轮计算的目标函数不再是全体样本误差，而仅是单个样本误差，即每次只代入计算一个样本目标函数的梯度来更新权重，再取下一个样本重复此过程，直到损失函数值停止下降或损失函数值小于某个可以容忍的阈值。

此过程简单，高效，通常可以较好地避免更新迭代收敛到局部最优解。其迭代形式为
$\large \theta_{i+1}=\theta_i-\alpha(h_{\theta}(x_0^{(j)},x_1^{(j)},\cdots,x_n^{(j)})-y_j)x_i^{(j)}$
但是由于，SG每次只使用一个样本迭代，若遇上噪声则容易陷入局部最优解。

1.3 小批量梯度下降算法(mini-batch)

小批量梯度下降算法是FG和SG的折中方案,在一定程度上兼顾了以上两种方法的优点。

每次从训练样本集上随机抽取一个小样本集，在抽出来的小样本集上采用FG迭代更新权重。

被抽出的小样本集所含样本点的个数称为batch_size，通常设置为2的幂次方，更有利于GPU加速处理。

特别的，若batch_size=1，则变成了SG；若batch_size=n，则变成了FG.其迭代形式为
$\large \theta_{i+1}=\theta_i-\alpha\sum_{j=t}^{t+x-1}(h_{\theta}(x_0^{(j)},x_1^{(j)},\cdots,x_n^{(j)})-y_j)x_i^{(j)}$

上式中，也就是我们从m个样本中，选择x个样本进行迭代(1<x<m),

1.4 随机平均梯度下降算法(SAG)

在SG方法中，虽然避开了运算成本大的问题，但对于大数据训练而言，SG效果常不尽如人意，因为每一轮梯度更新都完全与上一轮的数据和梯度无关。

随机平均梯度算法克服了这个问题，在内存中为每一个样本都维护一个旧的梯度，随机选择第i个样本来更新此样本的梯度，其他样本的梯度保持不变，然后求得所有梯度的平均值，进而更新了参数。

如此，每一轮更新仅需计算一个样本的梯度，计算成本等同于SG，但收敛速度快得多。

其迭代形式为：
$\large \theta_{i+1}=\theta _i-\frac{\alpha }{n}(h_\theta (x^{(j)}_0,x^{(j)}_1,...x^{(j)}_n)-y_j)x_i^{(j)}$

我们知道sgd是当前权重减去步长乘以梯度，得到新的权重。sag中的a，就是平均的意思，具体说，就是在第k步迭代的时候，我考虑的这一步和前面n-1个梯度的平均值，当前权重减去步长乘以最近n个梯度的平均值。
n是自己设置的，当n=1的时候，就是普通的sgd。
这个想法非常的简单，在随机中又增加了确定性，类似于mini-batch sgd的作用，但不同的是，sag又没有去计算更多的样本，只是利用了之前计算出来的梯度，所以每次迭代的计算成本远小于mini-batch sgd，和sgd相当。效果而言，sag相对于sgd，收敛速度快了很多。这一点下面的论文中有具体的描述和证明。
SAG论文链接：https://arxiv.org/pdf/1309.2388.pdf

小结

全梯度下降算法(FG)【了解】
- 在进行计算的时候,计算所有样本的误差平均值,作为我的目标函数
随机梯度下降算法(SG)【了解】
- 每次只选择一个样本进行考核
小批量梯度下降算法(mini-batch)【了解】
- 选择一部分样本进行考核
随机平均梯度下降算法(SAG)【了解】
- 会给每个样本都维持一个平均值,后期计算的时候,参考这个平均值

2.6 线性回归案例

学习目标

了解正规方程的api及常用参数
了解梯度下降法api及常用参数
知道如何对线性回归模型进行评估

1 线性回归API

sklearn.linear_model.LinearRegression(fit_intercept=True)
- 通过正规方程优化
- 参数
  - fit_intercept：是否计算偏置
- 属性
  - LinearRegression.coef_：回归系数
  - LinearRegression.intercept_：偏置
sklearn.linear_model.SGDRegressor(loss=“squared_loss”, fit_intercept=True, learning_rate =‘invscaling’, eta0=0.01)
- SGDRegressor类实现了随机梯度下降学习，它支持不同的loss函数和正则化惩罚项来拟合线性回归模型。
- 参数：
  - loss:损失类型
    - loss=”squared_loss”: 普通最小二乘法
  - fit_intercept：是否计算偏置
  - learning_rate : string, optional
    - 学习率填充
    - ’constant’: eta = eta0
    - ’optimal’: eta = 1.0 / (alpha * (t + t0)) [default]
    - ‘invscaling’: eta = eta0 / pow(t, power_t)
      - power_t=0.25:存在父类当中
    - 对于一个常数值的学习率来说，可以使用learning_rate=’constant’ ，并使用eta0来指定学习率。
- 属性：
  - SGDRegressor.coef_：回归系数
  - SGDRegressor.intercept_：偏置

sklearn提供给我们两种实现的API，可以根据选择使用

2 案例：波士顿房价预测

2.1 案例背景介绍

数据介绍

给定的这些特征，是专家们得出的影响房价的结果属性。我们此阶段不需要自己去探究特征是否有用，只需要使用这些特征。到后面量化很多特征需要我们自己去寻找

2.2 案例分析

回归当中的数据大小不一致，是否会导致结果影响较大。所以需要做标准化处理。

数据分割与标准化处理
回归预测
线性回归的算法效果评估

2.3 回归性能评估

均方误差(Mean Squared Error, MSE)评价机制：
$\Large MSE = \frac{1}{m}\sum_{i=1}^{m}(y^i-\hat{y})^2$
注： $y^i$ 为预测值， $\hat{y}$ 为真实值

sklearn.metrics.mean_squared_error(y_true, y_pred)
- 均方误差回归损失
- y_true:真实值
- y_pred:预测值
- return:浮点数结果

2.4 代码实现

导包

from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_squared_error
from sklearn.linear_model import SGDRegressor
from sklearn.linear_model import LinearRegression

正规方程

# 1.获取数据
data = load_boston()

# 2.数据集划分
x_train, x_test, y_train, y_test = train_test_split(data.data, data.target, random_state=22)

# 3.特征工程-标准化
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)

# 4.机器学习-线性回归(正规方程)
estimator = LinearRegression()
estimator.fit(x_train, y_train)

# 5.模型评估
# 5.1 获取系数等值
y_predict = estimator.predict(x_test)
print("预测值为:\n", y_predict)
print("模型中的系数为:\n", estimator.coef_)
print("模型中的偏置为:\n", estimator.intercept_)

# 5.2 评价
# 均方误差
error = mean_squared_error(y_test, y_predict)
print("误差为:\n", error)

梯度下降法

# 1.获取数据
data = load_boston()

# 2.数据集划分
x_train, x_test, y_train, y_test = train_test_split(data.data, data.target, random_state=22)

# 3.特征工程-标准化
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.fit_transform(x_test)

# 4.机器学习-线性回归(特征方程)
estimator = SGDRegressor(max_iter=1000)
estimator.fit(x_train, y_train)

# 5.模型评估
# 5.1 获取系数等值
y_predict = estimator.predict(x_test)
print("预测值为:\n", y_predict)
print("模型中的系数为:\n", estimator.coef_)
print("模型中的偏置为:\n", estimator.intercept_)

# 5.2 评价
# 均方误差
error = mean_squared_error(y_test, y_predict)
print("误差为:\n", error)

我们也可以尝试去修改学习率

estimator = SGDRegressor(max_iter=1000,learning_rate="constant",eta0=0.1)

此时我们可以通过调参数，找到学习率效果更好的值。

小结

正规方程
- sklearn.linear_model.LinearRegression()
梯度下降法
- sklearn.linear_model.SGDRegressor(）
线性回归性能评估【知道】
- 均方误差：sklearn.metrics.mean_squared_error

2.7 欠拟合和过拟合

学习目标

掌握过拟合、欠拟合的概念
掌握过拟合、欠拟合产生的原因
知道什么是正则化，以及正则化的分类

1 定义

过拟合：一个假设在训练数据上能够获得比其他假设更好的拟合，但是在测试数据集上却不能很好地拟合数据(体现在准确率下降)，此时认为这个假设出现了过拟合的现象。(模型过于复杂)
欠拟合：一个假设在训练数据上不能获得更好的拟合，并且在测试数据集上也不能很好地拟合数据，此时认为这个假设出现了欠拟合的现象。(模型过于简单)
过拟合和欠拟合的区别：
- 欠拟合在训练集和测试集上的误差都较大
- 过拟合在训练集上误差较小，而测试集上误差较大

通过代码认识过拟合和欠拟合

绘制数据

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(666)
# np.random.uniform() 在[-3,3)范围内随机生成100个数
x = np.random.uniform(-3,3,size = 100)

# 转换成二维数组,变成一列
X = x.reshape(-1,1)
# np.random.normal() 生成100个符合正态分布的数,均值为0,标准差为1
y = 0.5* x**2 + x+2 + np.random.normal(0,1,size = 100)

from sklearn.linear_model import LinearRegression
estimator = LinearRegression()
estimator.fit(X,y)
y_predict = estimator.predict(X)

plt.scatter(x,y)
plt.plot(x,y_predict,color = 'r')
plt.show()

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-GXAeZjdK-1631190399729)(./pics/1.png)]

#计算均方误差
from sklearn.metrics import mean_squared_error
mean_squared_error(y,y_predict)

#3.0750025765636577

添加二次项，绘制图像

# 添加二次项
X2 = np.hstack([X,X**2])
estimator2 = LinearRegression()
estimator2.fit(X2,y)
y_predict2 = estimator2.predict(X2)

plt.scatter(x,y)
plt.plot(np.sort(x),y_predict2[np.argsort(x)],color = 'r')
plt.show()

#计算均方误差和准确率

from sklearn.metrics import mean_squared_error
mean_squared_error(y,y_predict2)

#1.0987392142417858

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-2rFw5c3P-1631190399731)(./pics/2.png)]

再次加入高次项，绘制图像，观察均方误差结果

X5 = np.hstack([X2,X**3,X**4,X**5,X**6,X**7,X**8,X**9,X**10])

estimator3 = LinearRegression()
estimator3.fit(X5,y)
y_predict5 = estimator3.predict(X5)

plt.scatter(x,y)
plt.plot(np.sort(x),y_predict5[np.argsort(x)],color = 'r')
plt.show()

error = mean_squared_error(y, y_predict5)
error

#1.0508466763764157

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-BVmS9ckb-1631190399732)(./pics/3.png)]

通过上述观察发现，随着加入的高次项越来越多，拟合程度越来越高，均方误差也随着加入越来越小。说明已经不再欠拟合了。

问题：如何判断出现过拟合呢？

将数据集进行划分：对比X、X2、X5的测试集的均方误差

X的测试集均方误差

X_train,X_test,y_train,y_test = train_test_split(X,y,random_state = 5)
estimator = LinearRegression()
estimator.fit(X_train,y_train)
y_predict = estimator.predict(X_test)

mean_squared_error(y_test,y_predict)
#3.153139806483088

X2的测试集均方误差

X_train,X_test,y_train,y_test = train_test_split(X2,y,random_state = 5)
estimator = LinearRegression()
estimator.fit(X_train,y_train)
y_predict = estimator.predict(X_test)
mean_squared_error(y_test,y_predict)
#1.111873885731967

X5的测试集的均方误差

X_train,X_test,y_train,y_test = train_test_split(X5,y,random_state = 5)
estimator = LinearRegression()
estimator.fit(X_train,y_train)
y_predict = estimator.predict(X_test)
mean_squared_error(y_test,y_predict)
#1.4145580542309835

2 原因以及解决办法

欠拟合原因以及解决办法
- 原因：学习到数据的特征过少
- 解决办法：
  - **1）添加其他特征项，**有时候我们模型出现欠拟合的时候是因为特征项不够导致的，可以添加其他特征项来很好地解决。
  - 2）添加多项式特征，这个在机器学习算法里面用的很普遍，例如将线性模型通过添加二次项或者三次项使模型泛化能力更强。
过拟合原因以及解决办法
- 原因：原始特征过多，存在一些嘈杂特征，模型过于复杂是因为模型尝试去兼顾各个测试数据点
- 解决办法：
  - 1）重新清洗数据，导致过拟合的一个原因也有可能是数据不纯导致的，如果出现了过拟合就需要我们重新清洗数据。
  - 2）增大数据的训练量，还有一个原因就是我们用于训练的数据量太小导致的，训练数据占总数据的比例过小。
  - 3）正则化
  - 4）减少特征维度

3 正则化

3.1 什么是正则化

在解决回归过拟合中，我们选择正则化。但是对于其他机器学习算法如分类算法来说也会出现这样的问题，除了一些算法本身作用之外（决策树、神经网络），我们更多的也是去自己做特征选择，包括之前说的删除、合并一些特征

如何解决？

在学习的时候，数据提供的特征有些影响模型复杂度或者这个特征的数据点异常较多，所以算法在学习的时候尽量减少这个特征的影响（甚至删除某个特征的影响），这就是正则化

注：调整时候，算法并不知道某个特征影响，而是去调整参数得出优化的结果

3.2 正则化类别

L2正则化
- 作用：可以使得其中W的变小，其中很小的w值会趋近于0，削弱某些特征的影响
- 优点：越小的参数说明模型越简单，越简单的模型则越不容易产生过拟合现象
- Ridge回归: from sklearn.linear_model import Ridge
L1正则化
- 作用：可以使得其中一些特征W的值直接为0，删除这些特征的影响
- LASSO回归: from sklearn.linear_model import Lasso
正则化案例

X10 = np.hstack([X2,X**3,X**4,X**5,X**6,X**7,X**8,X**9,X**10]) 
estimator3 = LinearRegression() 
estimator3.fit(X10,y) 
y_predict3 = estimator3.predict(X10) 

plt.scatter(x,y) 
plt.plot(np.sort(x),y_predict3[np.argsort(x)],color = 'r') 
plt.show()

# 打印回归系数
estimator3.coef_

## 展示结果
array([ 1.32292089e+00,  2.03952017e+00, -2.88731664e-01, -1.24760429e+00,
        8.06147066e-02,  3.72878513e-01, -7.75395040e-03, -4.64121137e-02,
        1.84873446e-04,  2.03845917e-03])

from sklearn.linear_model import Lasso  # L1正则
from sklearn.linear_model import Ridge  # 岭回归 L2正则

X10 = np.hstack([X2,X**3,X**4,X**5,X**6,X**7,X**8,X**9,X**10]) 
estimator_l1 = Lasso(alpha=0.005,normalize=True) # 调整alpha 正则化强度 查看正则化效果 normalize=True 数据标准化
estimator_l1.fit(X10,y) 
y_predict_l1 = estimator_l1.predict(X10) 

plt.scatter(x,y) 
plt.plot(np.sort(x),y_predict_l1[np.argsort(x)],color = 'r') 
plt.show()

estimator_l1.coef_  # Lasso 回归  L1正则 会将高次方项系数变为0

array([ 0.97284077,  0.4850203 ,  0.        ,  0.        , -0.        ,
        0.        , -0.        ,  0.        , -0.        ,  0.        ])

X10 = np.hstack([X2,X**3,X**4,X**5,X**6,X**7,X**8,X**9,X**10]) 
estimator_l2 = Ridge(alpha=0.005,normalize=True) # 调整alpha 正则化强度 查看正则化效果
estimator_l2.fit(X10,y) 
y_predict_l2 = estimator_l2.predict(X10) 

plt.scatter(x,y) 
plt.plot(np.sort(x),y_predict_l2[np.argsort(x)],color = 'r') 
plt.show()

estimator_l2.coef_   # l2 正则不会将系数变为0 但是对高次方项系数影响较大

array([ 9.91283840e-01,  5.24820573e-01,  1.57614237e-02,  2.34128982e-03,
        7.26947948e-04, -2.99893698e-04, -8.28333499e-05, -4.51949529e-05,
       -4.21312015e-05, -8.22992826e-07])

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-IEkiST1C-1631190399735)(./pics/26img.png)]

4 岭回归案例

4.1 岭回归的API

sklearn.linear_model.Ridge(alpha=1.0, fit_intercept=True,solver=“auto”, normalize=False)
- 具有l2正则化的线性回归
- alpha:正则化力度，也叫 λ
  - λ取值：0~1 1~10
- solver:会根据数据自动选择优化方法
  - sag:如果数据集、特征都比较大，选择该随机梯度下降优化
- normalize:数据是否进行标准化
  - normalize=False:可以在fit之前调用preprocessing.StandardScaler标准化数据
- Ridge.coef_:回归权重
- Ridge.intercept_:回归偏置

Ridge方法相当于SGDRegressor(penalty=‘l2’, loss=“squared_loss”),只不过SGDRegressor实现了一个普通的随机梯度下降学习，推荐使用Ridge(实现了SAG)

sklearn.linear_model.RidgeCV(_BaseRidgeCV, RegressorMixin)
- 具有l2正则化的线性回归，可以进行交叉验证
- coef_:回归系数

class _BaseRidgeCV(LinearModel):
    def __init__(self, alphas=(0.1, 1.0, 10.0),
                 fit_intercept=True, normalize=False,scoring=None,
                 cv=None, gcv_mode=None,
                 store_cv_values=False):

4.2 正则化程度的变化，对结果的影响

?-￡?????–????o|

正则化力度越大，权重系数会越小
正则化力度越小，权重系数会越大

4.3 岭回归实现波士顿房价预测

# 1.获取数据
data = load_boston()

# 2.数据集划分
x_train, x_test, y_train, y_test = train_test_split(data.data, data.target, random_state=22)

# 3.特征工程-标准化
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)

# 4.机器学习-线性回归(岭回归)
estimator = Ridge(alpha=1)
# estimator = RidgeCV(alphas=(0.1, 1, 10))
estimator.fit(x_train, y_train)

# 5.模型评估
# 5.1 获取系数等值
y_predict = estimator.predict(x_test)
print("预测值为:\n", y_predict)
print("模型中的系数为:\n", estimator.coef_)
print("模型中的偏置为:\n", estimator.intercept_)

# 5.2 评价
# 均方误差
error = mean_squared_error(y_test, y_predict)
print("误差为:\n", error)

小结

欠拟合【掌握】
- 在训练集上表现不好，在测试集上表现不好
- 解决方法：
  - 继续学习
    - 1.添加其他特征项
    - 2.添加多项式特征
过拟合【掌握】
- 在训练集上表现好，在测试集上表现不好
- 解决方法：
  - 1.重新清洗数据集
  - 2.增大数据的训练量
  - 3.正则化
  - 4.减少特征维度
正则化【掌握】
- 通过限制高次项的系数进行防止过拟合
- L1正则化
  - 理解：直接把高次项前面的系数变为0
  - Lasso回归
  - from sklearn.linear_model import Lasso
- L2正则化
  - 理解：把高次项前面的系数变成特别小的值
  - 岭回归

2.8 模型的保存和加载

学习目标

知道sklearn中模型的保存和加载

1 sklearn模型的保存和加载API

from sklearn.externals import joblib
- 保存：joblib.dump(estimator, ‘test.pkl’)
- 加载：estimator = joblib.load(‘test.pkl’)
- 注意：0.21版本以下可以使用sklearn.externals.joblib，新版本需要安装joblibpip install joblib，import joblib

2 线性回归的模型保存加载案例

# 1.获取数据
data = load_boston()

# 2.数据集划分
x_train, x_test, y_train, y_test = train_test_split(data.data, data.target, random_state=22)

# 3.特征工程-标准化
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)

# 4.机器学习-线性回归(岭回归)
# 4.1 模型训练
estimator = Ridge(alpha=1)
estimator.fit(x_train, y_train)

# 4.2 模型保存
joblib.dump(estimator, "./data/test.pkl")

# 4.3 模型加载
estimator = joblib.load("./data/test.pkl")

# 5.模型评估
# 5.1 获取系数等值
y_predict = estimator.predict(x_test)
print("预测值为:\n", y_predict)
print("模型中的系数为:\n", estimator.coef_)
print("模型中的偏置为:\n", estimator.intercept_)

# 5.2 评价
# 均方误差
error = mean_squared_error(y_test, y_predict)
print("误差为:\n", error)

3 小结

sklearn.externals import joblib【知道】
- 保存：joblib.dump(estimator, ‘test.pkl’)
- 加载：estimator = joblib.load(‘test.pkl’)
- 注意：
  - 1.保存文件，后缀名是**.pkl
  - 2.加载模型是需要通过一个变量进行承接

2.9 线性回归应用-回归分析

学习目标

知道线性回归的常见落地场景

1、什么是回归分析

回归是研究自变量x对因变量y影响的一种数据分析方法
- 最简单的回归模型是一元线性回归，可以表示为Y=β0+β1x+ε，其中Y为因变量，x为自变量，β1为影响系数，β0为截距，ε为随机误差。
- 回归分析是广泛应用的统计分析方法，可用于分析自变量和因变量的影响关系（通过自变量求因变量），也可以分析自变量对因变量的影响方向（正向影响还是负向影响）。
- 回归分析的主要应用场景是进行预测和控制，例如计划制定、KPI制定、目标制定等；也可以基于预测的数据与实际数据进行比对和分析，确定事件发展程度并给未来行动提供方向性指导。
- 常用的回归算法包括线性回归、多项式回归等
- 回归分析的优点是数据模式和结果便于理解，如线性回归用y=ax+b的形式表达，在解释和理解自变量与因变量关系式相对容易；在基于函数公式的业务应用中，可以直接使用代入法求解，因此应用起来比较容易。
- 回归分析的缺点是只能分析少量变量之间的相互关系，无法处理海量变量间的相互作用关系，尤其是变量共同因素对因变量的影响程度。

2、回归分析落地场景

在各种媒体上投放的广告对最终销售所产生的效果研究
- 公司可以投入的营销渠道
  - 传统大众媒体：电视广播户外广告
  - 直销媒体：电子邮件，短信，电话
  - 数字媒体：app 微信社交应用
- 通过回归分析可以回答
  - 不同营销渠道是如何促进销售的
  - 如何调整营销组合使每一份支出获取最大收益
  - 同时在不同渠道进行广告营销，哪个效果更明显
- 销售量 = 营销变量 + 误差因素
  - 营销变量：可控的渠道投入
    - 线上产品：微信微博头条
    - 传统产品：电商微信户外电视
  - 误差因素：不可控的所有因素
    - 经济大环境，季节，假期，对手
- 营销变量和销售量之间是线性关系
  - 营销投入越大，销售量也会对应的逐步提高
- 回归分析模型：销售额 =93765+0.3* 百度+0.15 * 社交媒体+0.05 *电话直销+0.02 * 短信
  - 线性回归模型，假设解释变量和因变量之间是线性关系，但实际情况，销售收入不会随着广告的投入而一直上升
  - 使用回归模型的结果，最主要的还是观察各个因素的大小做横向对比
回归分析的结果，着重于不同X对于Y影响的对比，直接预测Y的场景较少

3、回归分析实战

销售额预测分析

快消企业，分析目的
- 对商超门店的销售额进行预测
- 量化自身所能控制的各种促销因素所能产生的效果
- 对营销资源做出合理规划
传统快消企业，数据特点
- 聚合类的数据
- 渠道众多，无法精准了解用户
本例中，通过回归分析实现对各类因素投入产出比做出评估
- 分析数据
  - 电视广告，线上，线下，门店内，微信渠道等促销投入和销售额之间的关系
- 数据说明（以月为观测窗口）
  - Revenue 门店销售额
  - Reach 微信广告次数
  - Local_tv 本地电视广告投入
  - Online 线上广告投入
  - Instore 门店内海报等投入
  - Person 门店促销人员
  - Event 促销事件
    - cobranding 品牌联合促销
    - holiday 节假日
    - special 门店特别促销
    - non-event 无促销活动
- 分析流程：数据概况分析->单变量分析->相关性分析与可视化->回归模型
  - 数据概况分析
    - 数据行/列数量
    - 缺失值分布
  - 单变量分析
    - 数字型变量的描述指标（平均值，最大最小值，标准差）
    - 类别型变量（多少个分类，各自占比）
  - 相关性分析与可视化
    - 按类别交叉对比
    - 变量之间的相关性分析
    - 散点图/热力图
  - 回归分析
    - 模型建立
    - 模型评估与优化
代码

import pandas as pd
#数据读取#
#index_col=0 ，数据的第一列是索引，指定索引列
store=pd.read_csv('data/store_rev.csv',index_col=0)

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Env28gXu-1631190399737)(pics/p&g_regression1.png)]

#数据的基本信息
#发现local_tv有50多个空值
#发现event是object,即类别型变量
store.info()

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-1bWVRy7F-1631190399737)(pics/p&g_regression2.png)]

#统计各个列哪些是空值
#发现local_tv有56个空值
store.isnull().sum()

'''
revenue      0
reach        0
local_tv    56
online       0
instore      0
person       0
event        0
dtype: int64
'''

#了解数据的分布
#判断数据是否符合业务场景
store.describe()

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-dtR7jUmJ-1631190399738)(pics/p&g_regression3.png)]

#了解event的具体值
store.event.unique()
#array(['non_event', 'special', 'cobranding', 'holiday'], dtype=object)
#这些类别对应的revenue(销售额)是怎样的
store.groupby(['event'])['revenue'].describe()

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-cU5M1wHr-1631190399739)(pics/p&g_regression4.png)]

#这几个类别对应的local_tv（本地电视广告投入）是怎样的
store.groupby(['event'])['local_tv'].describe()

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Mu28SvwC-1631190399739)(pics/p&g_regression5.png)]

相关性分析

#所有变量，任意两个变量相关分析
#local_tv,person,instore是比较好的指标，与revenue相关度高
store.corr()

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-yjIWvUKY-1631190399740)(pics/p&g_regression7.png)]

#其他变量与revenue的相关分析
#sort_values 将revenue排序，ascending默认升序，False为降序排列
#看到前3个相关变量为local_tv,person,instore
store.corr()[['revenue']].sort_values('revenue',ascending=False)
'''
	               revenue
revenue	           1.000000
local_tv	       0.602114
person	           0.559208
instore	           0.311739
online	            0.171227
event_special	    0.033752
event_cobranding	-0.005623
event_holiday	    -0.016559
event_non_event	    -0.019155
reach	            -0.155314
'''

可视化分析

#可视化分析
import seaborn as sns
import matplotlib.pyplot as plt
#线性关系可视化
#斜率与相关系数有关
sns.regplot(x='local_tv',y='revenue',data=store)

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-UKqwBqOB-1631190399741)(pics/p&g_regression8.png)]

#线性关系可视化
sns.regplot(x='person',y='revenue',data=store)

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-xJrACbSX-1631190399742)(pics/p&g_regression9.png)]

sns.regplot(x='instore',y='revenue',data=store)

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-fcdcKFnX-1631190399743)(pics/p&g_regression10.png)]

线性回归分析

#删除缺失值，数据有缺失，不处理会报错，需要处理缺失值
store.dropna(inplace=True)

#或者填充缺失值
#缺失值处理,填充0
store=store.fillna(0)
#缺失值处理,均值填充
store=store.fillna(store.local_tv.mean())
store.info()
'''
<class 'pandas.core.frame.DataFrame'>
Int64Index: 985 entries, 845 to 26
Data columns (total 10 columns):
revenue             985 non-null float64
reach               985 non-null int64
local_tv            985 non-null float64
online              985 non-null int64
instore             985 non-null int64
person              985 non-null int64
event_cobranding    985 non-null uint8
event_holiday       985 non-null uint8
event_non_event     985 non-null uint8
event_special       985 non-null uint8
dtypes: float64(2), int64(4), uint8(4)
memory usage: 57.7 KB
'''

#设定自变量和因变量
y=store['revenue']
#第一次三个 
x=store[['local_tv','person','instore']]
#第二次四个 
#x=store[['local_tv','person','instore','online']]

#数据标准化处理
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler()
x1 = scaler.fit_transform(x)


from sklearn.linear_model import LinearRegression
# 实例化api
model=LinearRegression()
# 训练模型
model.fit(x1,y)
# LinearRegression(copy_X=True, fit_intercept=True, n_jobs=None, normalize=False)

# 自变量系数
model.coef_
# array([41478.6429907 , 48907.03909284, 26453.89791677])

# 模型的截距
model.intercept_
# -17641.46438435701
# 最后得到x和y的关系为:y=41478*local_tv + 48907*person + 26453*instore - 17641

# 模型的评估,x为'local_tv','person','instore'
y_predict=model.predict(x)#计算y预测值
from sklearn.metrics import mean_squared_error
mean_squared_error(y,y_predict)
# 1.9567577917634842e+18

4 结果解读

注意应用回归模型时研究自变量是否产生变化
- 在应用回归模型做预测时，必须研究对因变量产生影响的自变量是否产生变化，主要考察两个方面：
  - 是否产生了新的对因变量影响更大的自变量
    - 在建立回归模型时，需要综合考虑自变量的选择问题。如果遗漏了重要的变量，那么模型很可能无法正确反映实际情况，而且参数估计是有偏的，此时的回归模型极其不稳定且方差较大。
    - 同样在应用回归模型时，仍然需要重新评估该问题是否发生。例如，在做用户订单金额预测时是基于正常销售状态下的变量实现的；但当发生大型促销活动且促销活动因素没有被纳入回归模型中时，原来的回归模型则无法有效预测。
  - 原有自变量是否仍然控制在训练模型时的范围之内。
    如果有自变量的变化超过训练模型的范围，那么原来的经验公式可能无法在新的值域范围下适用，这种情况下通常需要重新做研究和建模。
    - 假设我们建立了一个回归模型，可以广告投放费用预测广告点击率，在训练回归模型时的广告费用在[0，1000]区间内，但在广告费用超过1000（例如2000）时，则无法保证最终预测效果的有效性。
回归算法按照自变量的个数分为一元回归和多元回归，按照影响是否是线性分为线性回归和非线性回归。在面对不同回归方法的选择时，注意参考以下因素：
- 入门的开始——简单线性回归。如果是学习为主，那么不需要选择多么强大的模型，基于最小二乘法的普通线性回归最合适；同时，它适合数据集本身结构简单、分布规律有明显线性关系的场景。
- 如果自变量数量少或经过降维后得到了可以使用的二维变量（包括预测变量），那么可以直接通过散点图发现自变量和因变量的相互关系，然后选择最佳回归方法。
- 如果经过基本判断发现自变量间有较强的共线性关系，可以考虑岭回归。
- 如果在高维度变量下，使用正则化回归方法效果更好，例如Lasso、Ridge
- 如果注重模型的可解释性，那么容易理解的线性回归、多项式回归比较适合。