[人工智能]Paper Reading《Fastformer Additive Attention Can Be All You Need 》

Paper Reading《Fastformer: Additive Attention Can Be All You Need 》

Paper url；笔者写作时作者Github尚未开源。Unofficial版本复现：TF版本，Pytorch版本，Keras版本；以及推荐一位Youtube上的大神Yannic Kilcher对本文进行的讲解。

1. Intuition

传统Transformer机制囿于512个token文本长度限制，涌现出了以下几种当前主流的Transformer变种，但同时也也存在着相应的缺点：

1. 使用稀疏注意力机制降低计算复杂度。e.g. Longformer, BigBird.

   缺点：自注意力机制需要更多的tokens参与运算，大幅度提升了时间和计算开销，速度慢。

2. 利用hashing编码技术加速自注意力机制的计算。e.g. Reformer

   缺点：计算复杂度常数很大，在处理长度有限的常见序列时效率很低。

3. 近似地计算自注意力。e.g. Linformer

   缺点：以上下文标记的方式接近自注意力，不是文本建模的最佳方法。当序列长度很长时计算效率低。

2. Fast-former Architecture

2.1 回顾下Self-Attention

$\text{Attention}(Q,K,V)=\text{softmax}(\frac{Q{K}^T}{\sqrt{d_k}})V$

先对$Q,K$做点乘（i.e. dot-product）得到二者的相似度矩阵，矩阵的每一行都是一个query和所有key的相似性；然后用$\sqrt{d_k}$进行scaling，之后用softmax函数后再和$V$相乘。

如何理解Self-Attention的Q，K ，V向量

目标是让模型能够各个单词词向量在上下文向量中代表着是哪种含义。

• Key vector $K$:

  describes what the content of this token is so far, which allows the token to advertise what is has to offer。更像句子本身的内容（addressable representation）

• Query Vector $Q$：

  means what does this token wanna know about the other tokens in the sequence. 更像我想从别的token那得到什么信息。

  所以 $K$ and $Q$ 通常是不一样的

  通过计算$Q{W}^Q$以及$K{W}^K$的内积的softmax值表征了：针对于输入句中的每一个token所代表的信息想最终聚合到最后输出句子的token的。对每一个token都会算我们想要他这个token有多少信息“作用到”输出句子上。

• Value Vector $V$:

  通过前文softmax得到的分布，我们输入到下一个layer的乘积。类似于斜率

2.2 Architecture

根据input text的embedding matrix，记为$E\in {\mathbb{R}}^{N\times d}$，每个token代表的列向量记$[e_1,e_2,?,e_N]$。

1. 通过线性变换层得到矩阵$Q,K,V$的映射，$Q,K,V\in {\mathbb{R}}^{N\times d}$（此处为原文typo写为了$R^{d\times d}$），$Q=[q_1,q_2,?,q_N]$，$K=[k_1,k_2,?,k_N]$，$V=[v_1,v_2,?,v_N]$.

2. 利用加性注意力价值概括融合（summarize）$Q$矩阵的信息得到浓缩上下文信息的global query vector。

   那$Q$矩阵转到$q$向量的权重如何得到？利用softmax的思想计算：
   $${\alpha }_i=\frac{\exp \left({\mathbf{w}}_q^T{\mathbf{q}}_i/\sqrt{d}\right)}{{\sum }_{j=1}^N\exp \left({\mathbf{w}}_q^T{\mathbf{q}}_j/\sqrt{d}\right)}$$
   其中$w_q\in {\mathbb{R}}^d$是一个要学习的向量参数。$\alpha \in {\mathbb{R}}^{N\times 1}$

   则global query vector即为$\mathbf{q}={\sum }_{i=1}^N{\alpha }_i{\mathbf{q}}_i$。$\mathbf{q}\in {\mathbb{R}}^{N\times 1}$

3. 我们知道在经典Transformer中我们是利用点积来对$Q,K$之间交互计算相似度进行建模，但$Q?K^T$会带来二次的复杂度，那我们加性注意力机制如何降低运算复杂度的呢？

   • 拼接：简单地连接两个向量不能考虑它们之间的相互作用。
   • 相加：只能得到两个向量之间的线性相互作用，但也不能学习准确的上下文表示
   • **element-wise product：**对两个变量之间的非线性相互作用进行建模，这可能有助于对长序列的复杂上下文进行建模。(Xiang Wang, et al. 2017.)

   所以在此通过global query vector和$K$矩阵计算element-wise product得到global context-aware key matrix，即$p_i=q?k_i$，其实相对于传统transformer的步骤就是把$q_i?k_i$变成了$q?k_i$，可以叫他全局注意力矩阵，因为$q$向量是综合了所有token的信息。

   ※其实将上式展开可以看到：$p_i=k_i{\sum }_j{\alpha }_j{q}_j={\sum }_j{\alpha }_j{q}_j{k}_j$，虽然我们有二次成绩，但是我们并不会有二次的运算复杂度，Why？

   因为我们并没有原始的Transformer那样直接计算 softmax { ( [ Q W Q ? ( K W K ) T ] / d } \text{softmax}\{([QW^Q\cdot (KW^K)^T]/\sqrt{d}\} softmax{([QWQ?(KWK)T]/d ?}，该部分需要把每个序列中的每个位置的token两两组合，即需要将两个$n\times d$的矩阵相乘，计算复杂度为$O(n^2)$。

   而Fast-former将$Q\in {\mathbb{R}}^{N\times d}$压缩为$q\in {\mathbb{R}}^{N\times 1}$之后，就成为了在序列上的线性运算从而摆脱了softmax的非线性运算的影响，这也就是他为什么叫additive attention，也是本paper的trick所在。

   在此再对$p$也进行加性注意力机制，其每个$p_i$的权重为：
   $${\beta }_i=\frac{\exp \left({\mathbf{w}}_k^T{\mathbf{p}}_i/\sqrt{d}\right)}{{\sum }_{j=1}^N\exp \left({\mathbf{w}}_k^T{\mathbf{p}}_j/\sqrt{d}\right)}$$
   其中$w_k\in {\mathbb{R}}^d$是一个要学习的向量参数。

   则global key vector即为$\mathbf{k}={\sum }_{i=1}^N{\beta }_i{\mathbf{p}}_i$。

4. 同于以上步骤，通过global query vector $q$计算global context-aware key matrix得到global key vector$k$的过程，我们再用global key vector$k$来得到global key-value matrix，记为$u$

   也即$u_i=k?v_i$。因为后面不再需要value vector再去启发别的向量，所以将$u_i$经过一层线性变换层得到输出$\mathbf{R}=\left[{\mathbf{r}}_1,{\mathbf{r}}_2,\dots ,{\mathbf{r}}_N\right]\in {\mathbb{R}}^{N\times d}$

   至此，每个key和value向量都可以与global query/key向量交互以学习上下文表示。

5. 最后，将经过线性变换后的输出$R\in {\mathbb{R}}^{N\times d}$加上global query vector $q\in {\mathbb{R}}^{N\times 1}$，要注意二者维度不一样，即在$R$的每一行都加上向量$q$即为Fast-former的final outpout。（这一步第一次看感觉大家也觉得有点trick，作者未做出原因解释。）

6. 以上1-5为one head，多个Fast-former层叠加成Multi-head机制。通过借鉴Linformer(Wang et al. 2020)的参数共享技术，共享了value和query的线性变换层参数以降低参数量和过拟合的风险。（作者并未做出原因解释，可能是Linformer中做出了相应的解释？）

2.3 Complexity Analysis

对于global query and key vectors计算复杂度都是$O(N?d)$，总的计算复杂度为$O(N?d{)}^2$，对比于原始经典Transformer则为$O(N^2?d)$

3. Experiments

实验中使用Glove Embedding初始化token向量矩阵，本文选取了文本分类、新闻推荐及文本摘要的数据集进行验证。（后面更新的version的paper故意加上了新闻推荐的内容。）

3.1 实验效果

实验结果如下所示：

综合来看竞争力不是很稳定。

在新闻推荐任务上的结果（MIND数据集）：

前面几种为常用的新闻推荐baselines。虽然最好的结果是集成的结果，但Fastformer还是比其他几个模型显著地高。

在文本摘要任务上的结果：

整体而言效果不错。

3.2 时间效率比较

可以看到Fast-former在时间效率上还是提升了很大一部分的。

3.3 不同组合特征的影响

针对2.2中第三点提到的问题，不同特征采用相加、拼接、点乘的组合方式的不同结果表现：

点乘的方式还是显著的好很多。

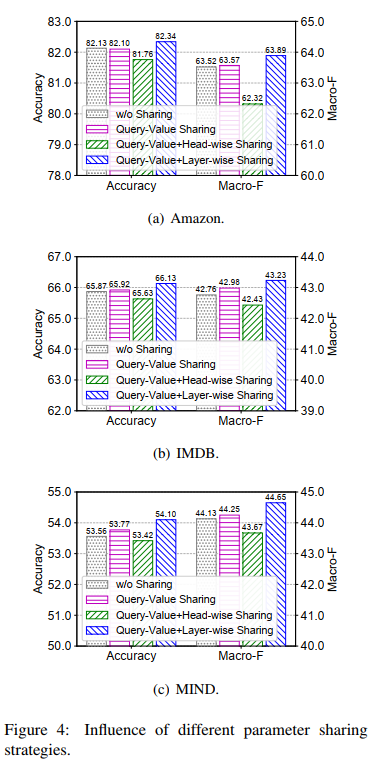
3.4 不同参数共享方式的影响

综合来看还是采用Q-结合Layer-wise的效果最好，但其实好的并不显著，零点几个点。

4. 一些问题

1. Fast-former的final output为何还要加上global query vector？理论上$R=(r_1,?,r_N)$已经融合了$QKV$三者的信息了，为何没有消融实验。只用global query vector，只用$R=(r_1,?,r_N)$效果又分别如何？

2. 这是否还是Transformer？

   Quote from Yannic Kilcher:

   Kind of like.

   为什么不是？其实本文所命名的Q，K，V并不是原始Transformer中所提到的概念，你其实可以继续明明Q，K，V，X，Y等等好几竖列一列一列地应用加性注意力机制，并不限于这三个QKV矩阵。

   为什么是？他真正体现为self-attention得地方还是用了softmax的地方即计算global query vector$q$的权重里面的$w_q$，他能够根据上下文动态地计算一个句子中不同的token的权重。结合原文的式子来看

   [1]${\alpha }_i=\frac{\exp \left({\mathbf{w}}_q^T{\mathbf{q}}_i/\sqrt{d}\right)}{{\sum }_{j=1}^N\exp \left({\mathbf{w}}_q^T{\mathbf{q}}_j/\sqrt{d}\right)}$

   和

   [2] $\mathbf{q}={\sum }_{i=1}^N{\alpha }_i{\mathbf{q}}_i$

   [1]中的$w_q$是self-attention中的query，${\mathbf{q}}_{\mathbf{i}}$是self-attention中的key，[2]中的${\mathbf{q}}_{\mathbf{i}}$也是self-attention中的value。

   而Fast-former后面的Key 和 Value都是根据global query vector 静态学习到的，没有自己的学习参数矩阵，每一个单独的头算出来一个query，他是什么后面就定死了，只能通过多头来实现全方位的语义挖掘。