[人工智能]机器学习基础（二）逻辑回归

机器学习—— 逻辑回归（Logistic regression）

本文主要是对 《机器学习》中的逻辑回归做一个简单的公式推导以及编码实现。该内容只涉及公式的推导，并不具体阐述公式含义。具体视频可以参考 吴恩达老师讲解的机器学习的逻辑回归。

1. 符号和定义

• 样本矩阵 $X=[x_1,x_2,?,x_n{]}^T\in R^{n\times d}$ , $x_i$ 表示第 i 个样本。
• 标签矩阵 Y = [ y 1 , y 2 , ? ? , y n ] T ∈ { 0 , 1 } n Y = [y_1,y_2,\cdots,y_n]^T \in \{0,1\}^ n Y=[y1?,y2?,?,yn?]T∈{0,1}n
• 权重向量 $\theta \in R^d$

2. 公式以及推导过程

2.1 假设函数

$$H_{\theta }(x_i)=\frac{1}{1+e^{?x_i\theta }}\text{\hspace{1em}(1)}$$

2.2 目标函数（代价函数）

原目标函数:

$$J(\theta )=\frac{1}{m}\sum _{i=1}^m?y_i\log (\frac{1}{1+e^{?x_i\theta }})?(1?y_i)\log (1?\frac{1}{1+e^{?x_i\theta }})$$

目标函数化简：化简只是为了方便后续的求导

$$\begin{array}{lcc}J(\theta )& =& \frac{1}{m}{\sum }_{i=1}^m?y_i\log (\frac{1}{1+e^{?x_i\theta }})?(1?y_i)\log (1?\frac{1}{1+e^{?x_i\theta }})\\ & =& \frac{1}{m}{\sum }_{i=1}^m{y}_i\log (1+e^{?x_i\theta })?(1?y_i)(?x_i\theta ?\log (1+e^{?x_i\theta }))\\ & =& \frac{1}{m}{\sum }_{i=1}^m{x}_i\theta +\log (1+e^{?x_i\theta })?y_i{x}_i\theta \end{array}\text{\hspace{1em}(2)}$$

2.3 梯度下降公式

$$\begin{gathered} {\theta }_j={\theta }_j?\alpha \frac{?J(\theta )}{{\theta }_j} \\ ?{\theta }_j={\theta }_j?\alpha \sum _{i=1}^m(H_{\theta }(x_i)?y_i)x_{ij}\text{\hspace{1em}(3)} \end{gathered}$$

推导过程：
$$\begin{array}{lcc}\frac{?J(\theta )}{?{\theta }_j}& =& \frac{1}{m}{\sum }_{i=1}^m\frac{?\left(x_i\theta +\log (1+e^{?x_i\theta })?y_i{x}_i\theta \right)}{?{\theta }_j}\\ & =& \frac{1}{m}{\sum }_{i=1}^m\frac{?x_i\theta }{?{\theta }_j}+\frac{?\log (1+e^{?x_i\theta })}{?{\theta }_j}?\frac{?y_i{x}_i\theta }{?{\theta }_j}\\ & =& \frac{1}{m}{\sum }_{i=1}^m{x}_{ij}?\frac{e^{?x_i\theta }}{1+e^{?x_i\theta }}{x}_{ij}?y_i{x}_{ij}\\ & =& \frac{1}{m}{\sum }_{i=1}^m(\frac{1}{1+e^{?x_i\theta }}?y_i)x_{ij}\end{array}\text{\hspace{1em}(4)}$$
$Note:$

• 求偏导数时，可以把矩阵形式写成多项相加的形式。
• 在求偏导的时候会发现有一个 $\frac{1}{m}$ 的系数，因此正确的迭代更新公式应该是${\theta }_j={\theta }_j?\frac{\alpha }{m}{\sum }_{i=1}^m(H_{\theta }(x_i)?y_i)x_{ij}$. 但是由于 $\alpha$ 是自定义初始化的，所以$\frac{1}{m}$ 并不影响优化结果。而且为了方便书写，通常省略该项。

等式 （4） 同样可以写成矩阵形式。矩阵形式如下：
$$\frac{?J(\theta )}{?{\theta }_j}=\frac{1}{m}(x^j{)}^T(\frac{1}{1+e^{?X\theta }}?Y).\text{\hspace{1em}(5)}$$
其中 $x^j$ 表示 矩阵 $X$ 的第 j 列 元素。同时 $\frac{1}{1+e^{?X\theta }}$ 表示的是点除，也就是说 每一个元素都被 1除。

3. matlab 编程实现

3.1 逻辑回归的梯度下降代码

以下代码是通过使用 梯度下降方式求解代价函数的最优解。

function [theta,value] = logisticGd(X,Y,alpha,maxIter)
% Input:
%   X: 数据矩阵 n x (d+1) 第一列为全 1 元素
%   Y: 标签矩阵 n x 1
%   alpha: 学习率, 该学习率可以通过查看 value 的值来调整。如果收敛的
%           太慢，可以设置大一点的值，如果value 震荡，则缩小 alpha
%   maxIter: 最大迭代次数
% Output:
%   theta: 最优解
%   value: 代价函数的函数值。用于查看收敛情况
[n,d] = size(X);
% 初始化 theta
theta = ones(d,1);
value = zeros(maxIter,1); % 目标函数值
for i = 1:maxIter
    for j = 1:d
        theta(j) = theta(j) - alpha/n*X(:,j)'*(1./(1+exp(-X*theta))-Y);
    end
    value(i) = sum((1-Y).*(X*theta)+log(1+exp(-X*theta)));
end
end

3.2 测试代码

数据下载链接：https://gitee.com/ljl745972609/ml_datasets/tree/master/an-exam/ex2

clc;clear all;
data = load(".\ex2\data1.txt");
data = mapminmax(data',0,1);
data = data';
[n,d] = size(data);
% 数据可视化
pos = data(:,d) == 1;
subplot(1,2,1);
scatter(data(pos,1),data(pos,2),"+r");
hold on;
scatter(data(~pos,1),data(~pos,2),"^b")
hold on;
xlabel("score1");
ylabel("score2");

rate = round(n*0.7);
% 梯度下降
Y = data(1:rate,d);
X = data(1:rate,1:d-1);
% 扩充 X，使得 x0 = 1;
X = [ones(rate,1),X];
[theta,value] = logisticGd(X,Y,5,150);
subplot(1,2,2);
plot(value);
title("The convergence curve of gradient descent");
ylabel("the value of J(\theta)");
xlabel("the number of iter");
% 验证性能
trustY = data(rate+1:n,d);
newX = [ones(n-rate,1),data(rate+1:n,1:d-1)];
preds = logisticPredict(newX,theta) > 0.5;
gdAcc = sum(preds == trustY)/length(rate+1:n);
% 绘制 gd 分类边界
ax = 0:0.01:1;
ay = -(theta(1)+theta(2)*ax)/theta(3);
subplot(1,2,1);
plot(ax,ay,"-k","LineWidth",1.2);
hold on;

3.3 使用 matlab 自带的优化函数求解

使用 fminunc 函数优化代价函数。该函数的具体使用可以查看官方文档。

3.3.1 第一步：编写代价函数代码

function cost = costFun(theta)
data = load(".\ex2\data1.txt");
data = mapminmax(data',0,1);
data = data';
[n,d] = size(data);
rate = round(n*0.7);
X = data(1:rate,1:d-1);
Y = data(1:rate,d);
% 扩充 X，使得 x0 = 1;
X = [ones(rate,1),X];

first = -Y.*log(sigmod(X*theta));
second = (1-Y).*log(1-sigmod(X*theta));
cost = sum(first-second)/ size(X,1);
end

3.3.2 测试该函数

clc;clear all;
data = load(".\ex2\data1.txt");
data = mapminmax(data',0,1);
data = data';
[n,d] = size(data);
% 数据可视化
pos = data(:,d) == 1;
scatter(data(pos,1),data(pos,2),"+r");
hold on;
scatter(data(~pos,1),data(~pos,2),"^b")
hold on;
xlabel("score1");
ylabel("score2");
% 划分测试集合训练集
rate = round(n*0.7);
Y = data(1:rate,d);
X = data(1:rate,1:d-1);
% 扩充 X，使得 x0 = 1;
X = [ones(rate,1),X];
% 使用 fminunc 优化
% 第二个参数是 costFun 的参数
[autoTheta,fval] = fminunc(@costFun,[0,0,0]');
newPred = sigmod(newX*autoTheta) > 0.5;
acc = sum(newPred == trustY)/length(rate+1:n);
fprintf("fminunc acc: %.3f\n",gdAcc,acc);
ax = 0:0.01:1;
newAy = -(autoTheta(1)+autoTheta(2)*ax)/autoTheta(3);
plot(ax,newAy,"-c","LineWidth",1.5);
legend("pos","neg","gd","fminunc");

注意：

• 使用 fminunc 优化时，优化的函数必须只有一个参数，并且该参数只能是 数值类型的数组或者标量
• 该函数默认使用的优化算法是 牛顿迭代算法，可以通过第三个参数自己设置优化算法。
• 该函数的停止标准为函数的梯度小于等于 1e-6.

实验结果：

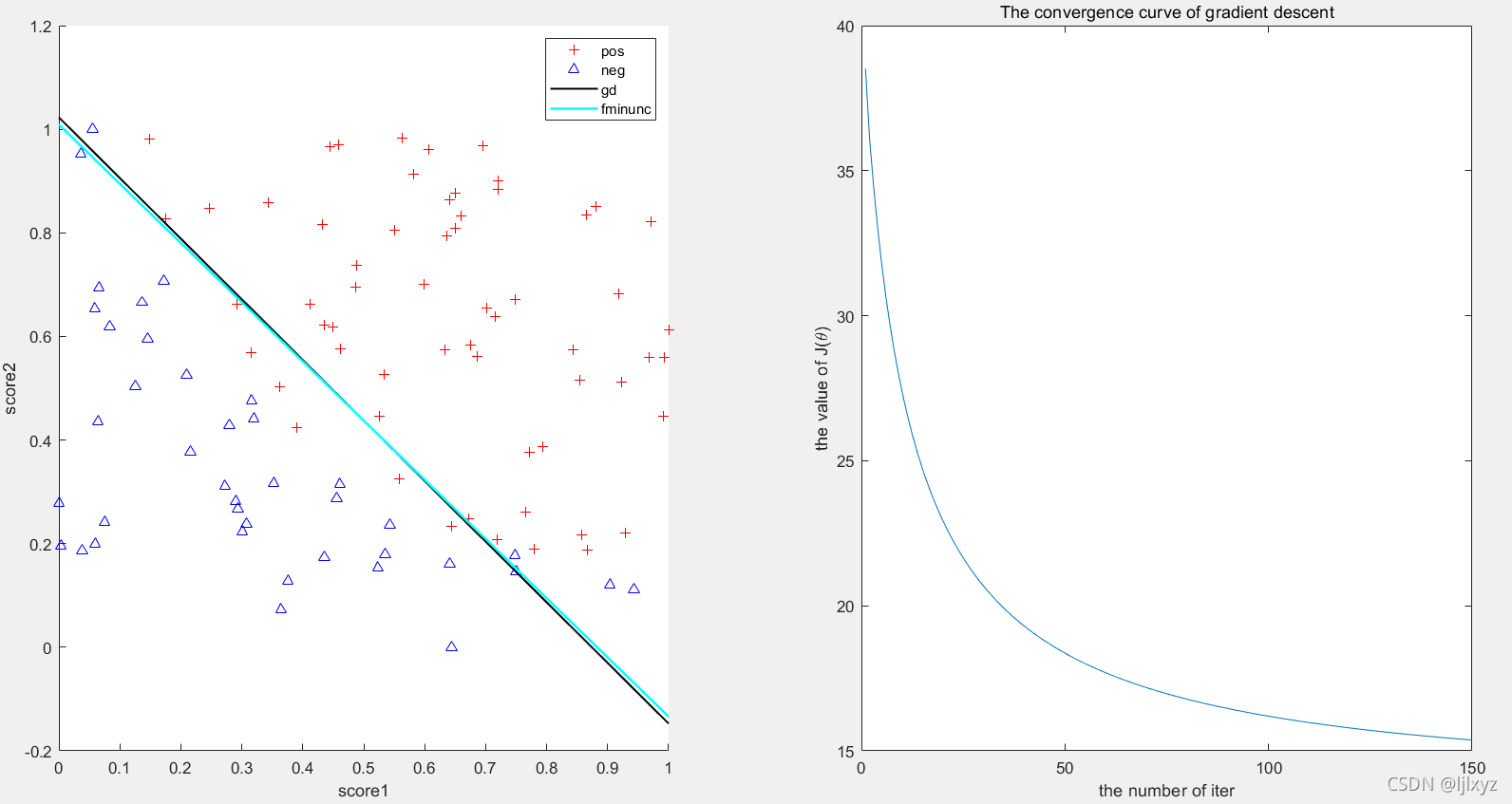
两种算法的分类精度都在 86.7% 左右