文章目录
一、离散卷积
第一种解释
1、什么是卷积过程
(1)铺垫
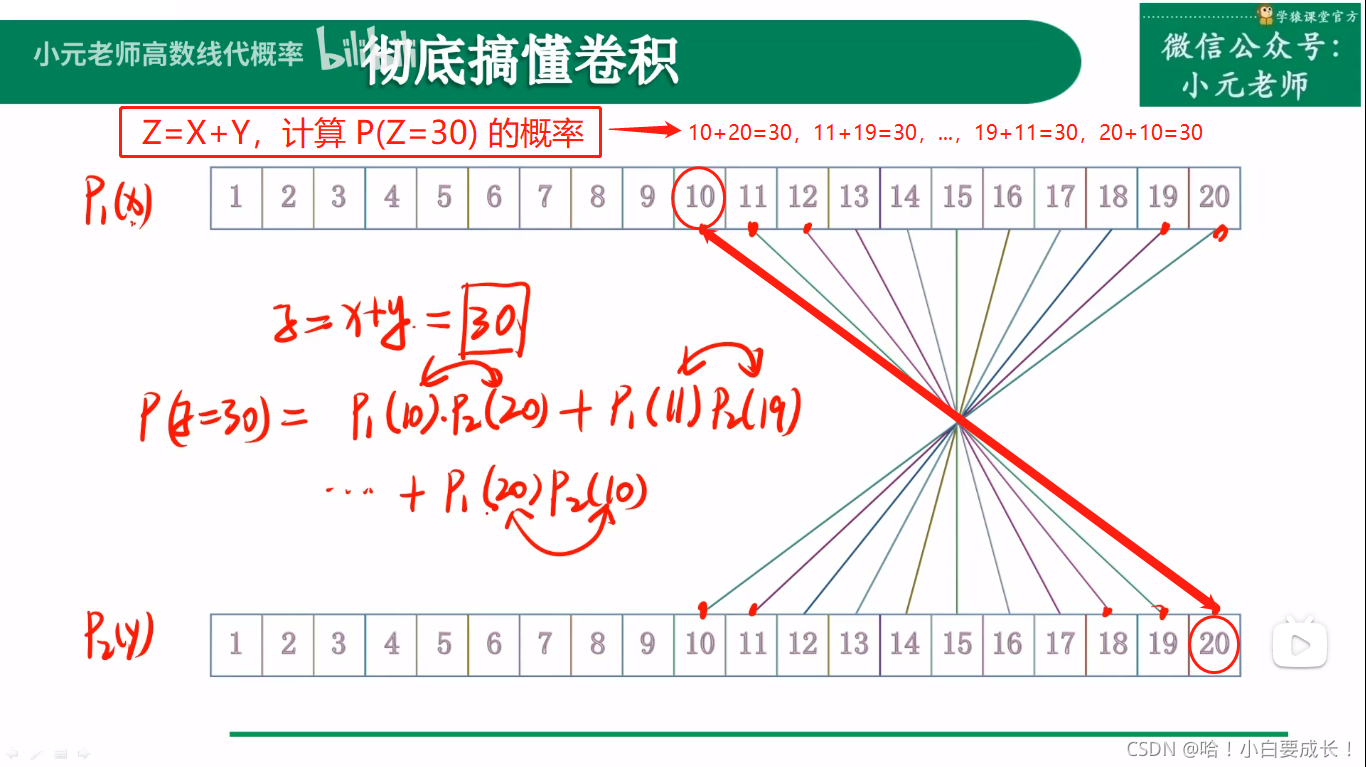

根据上图所示,如果要处理的数据非常大,那么这种交叉的连线很不合适,比较繁杂混乱。如果旋转一下,得到平行线就会很容易处理。下面就是这个旋转的过程。
(2)过程
第一步
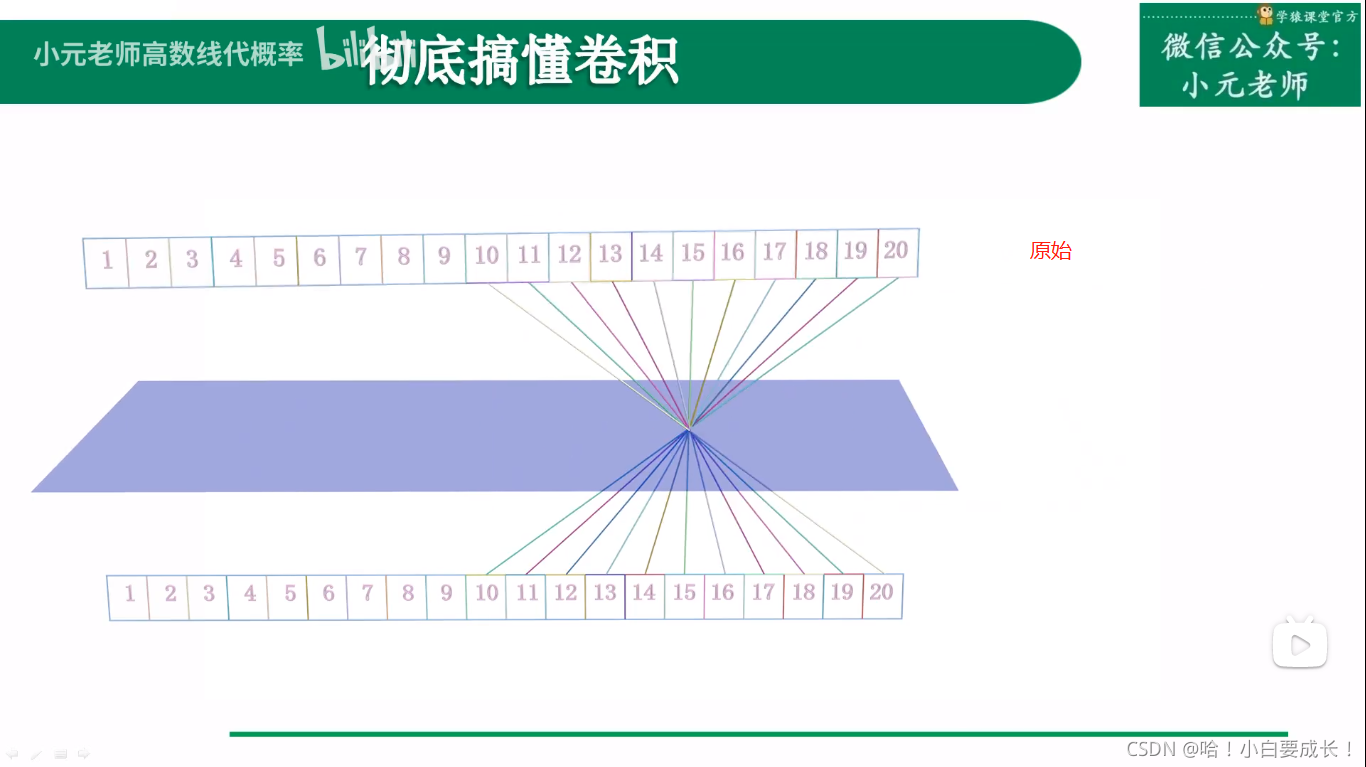
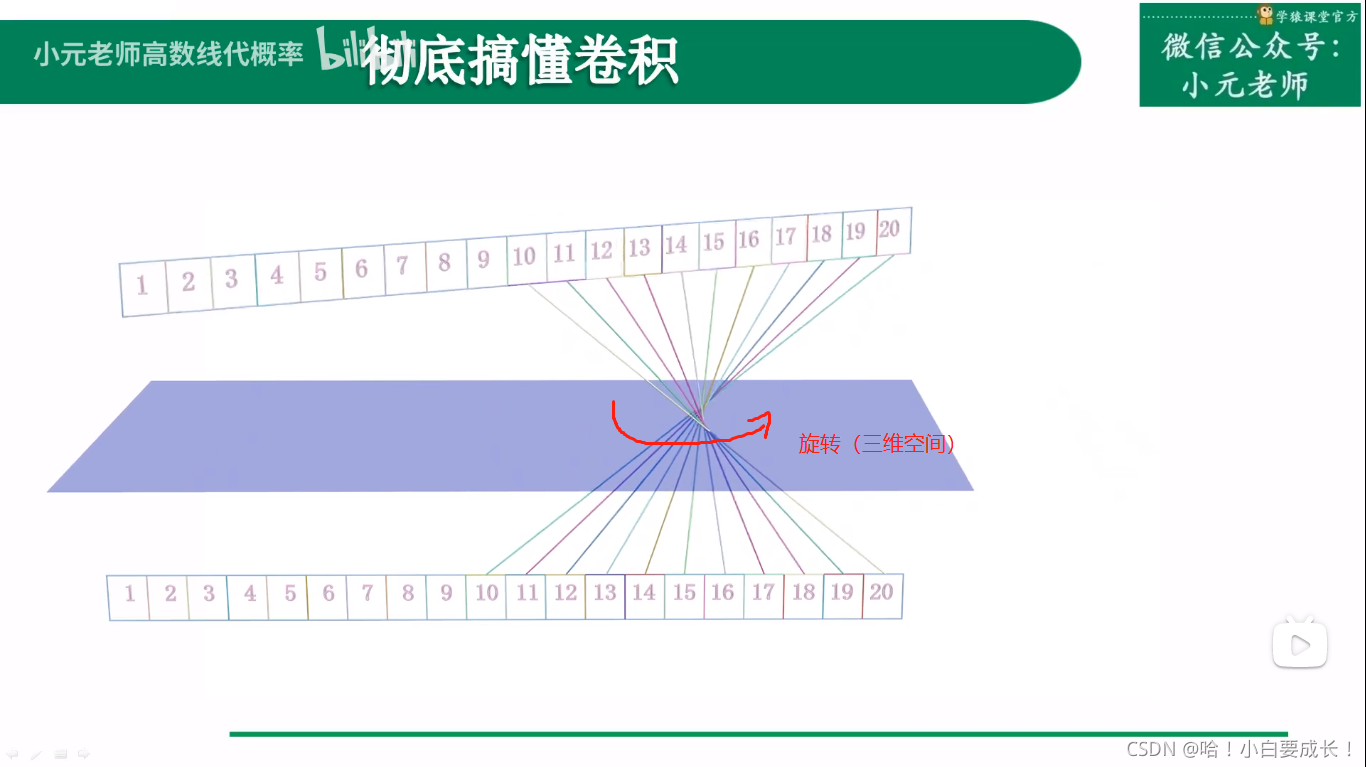
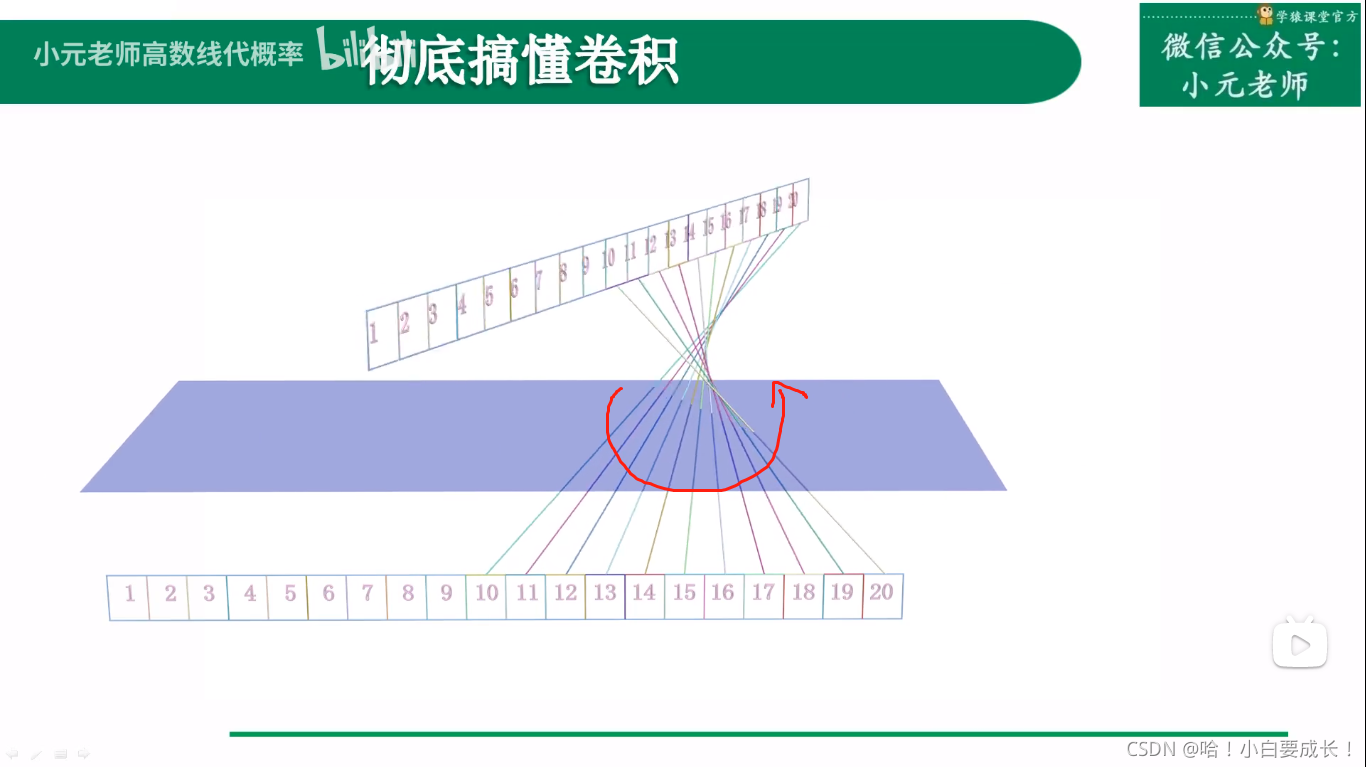
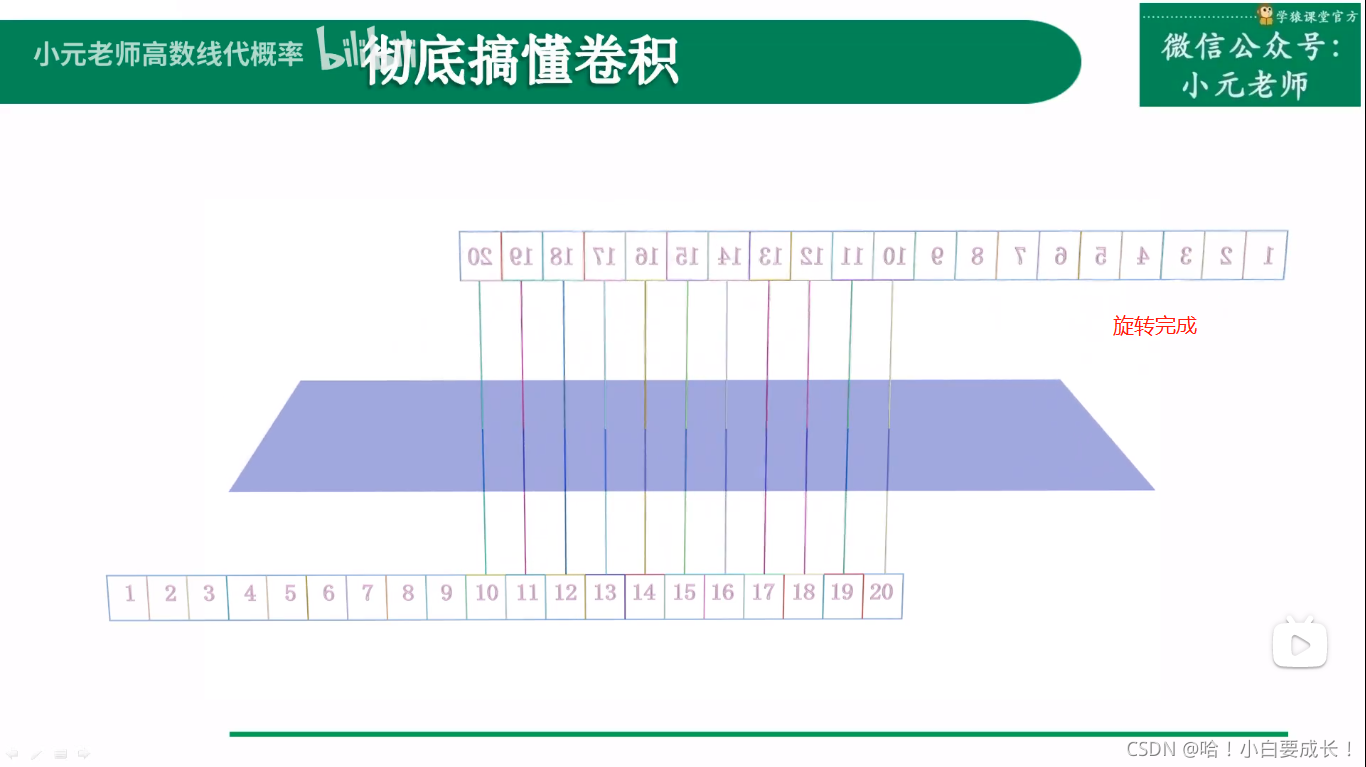
第二步:旋转数字。只旋转数字,不旋转数字的方框。
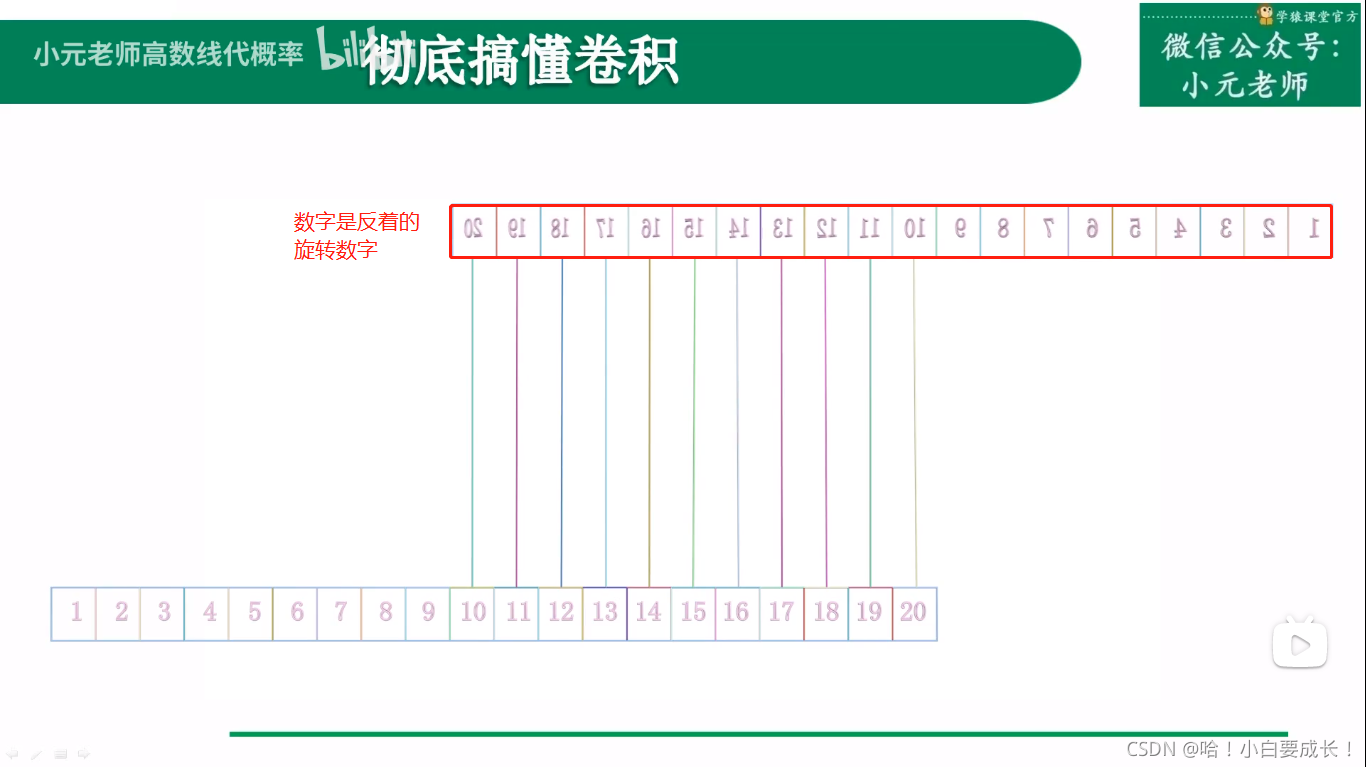
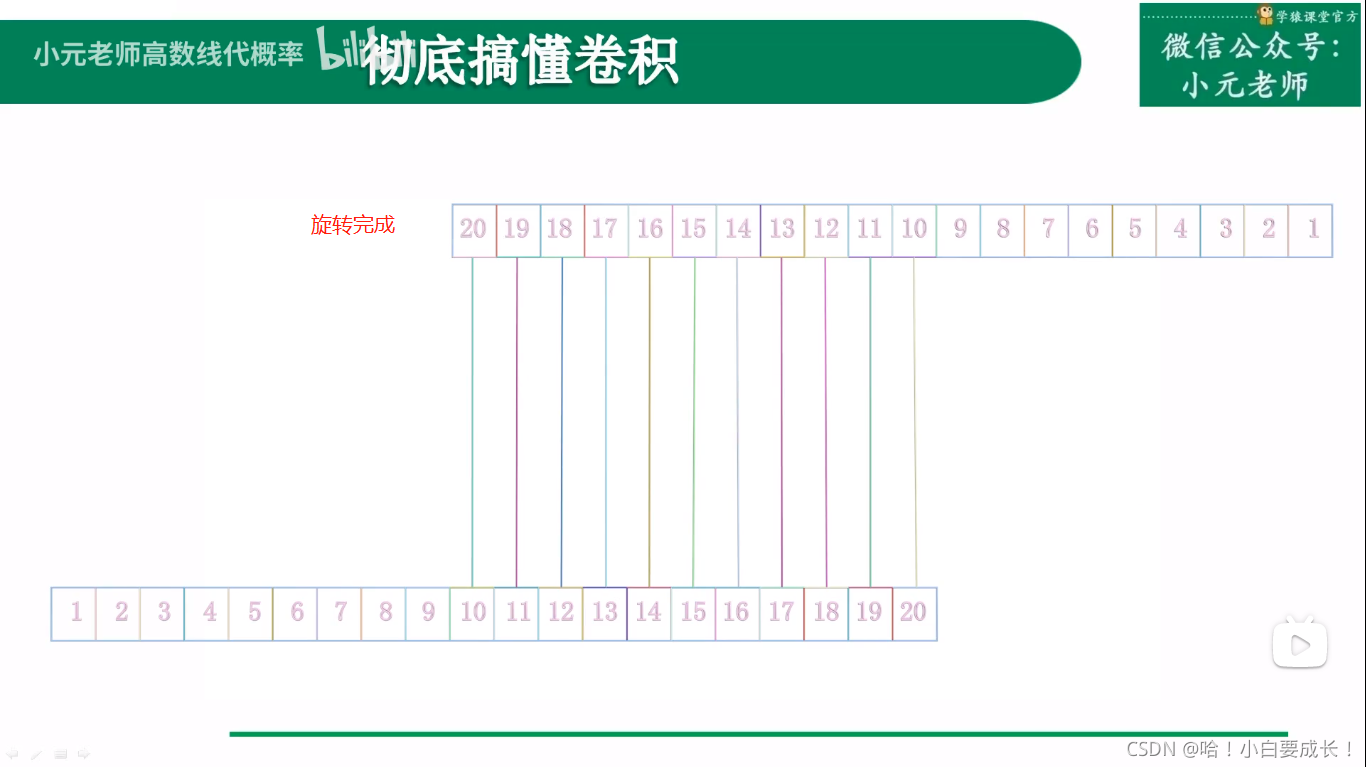
此时改变Z的取值,变得十分简单,只需要错位就行,很方便求卷积的过程

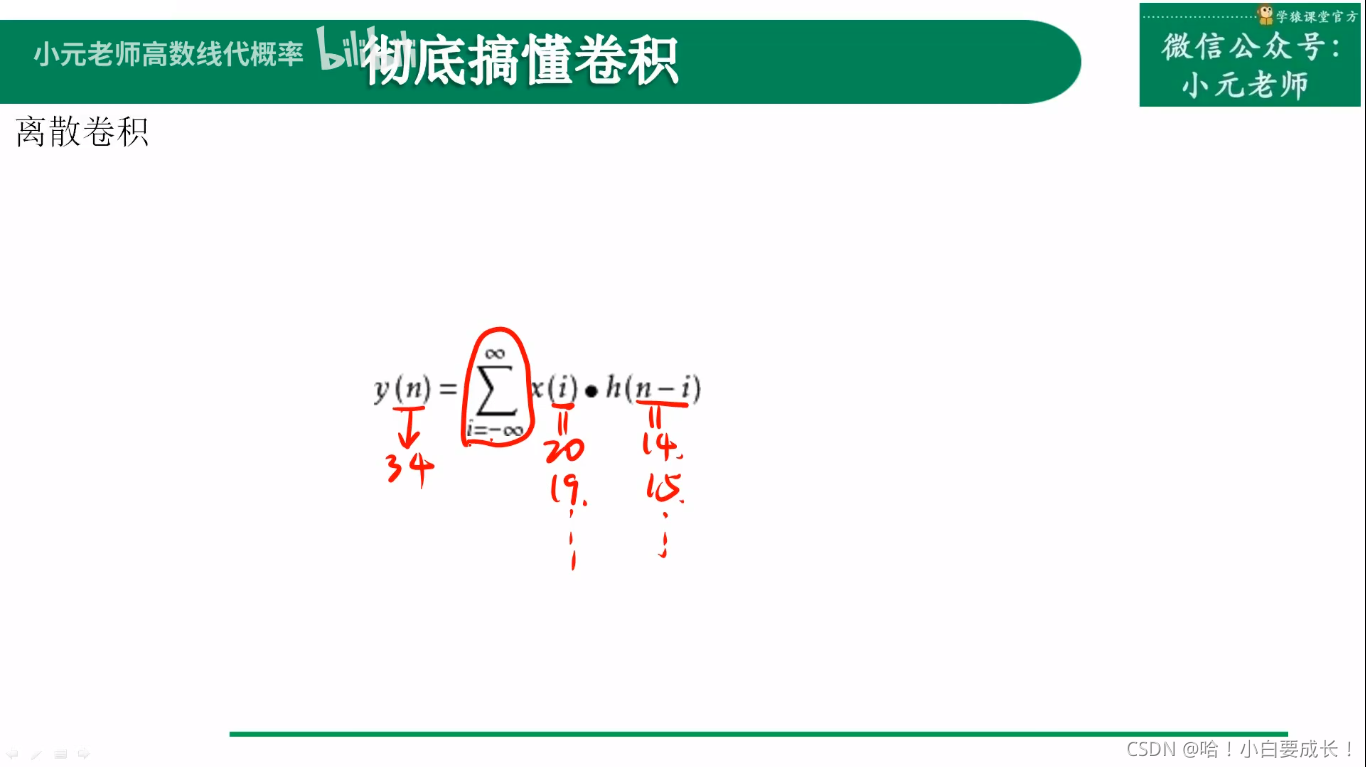
2、为什么叫“卷积”,哪里体现了“卷”

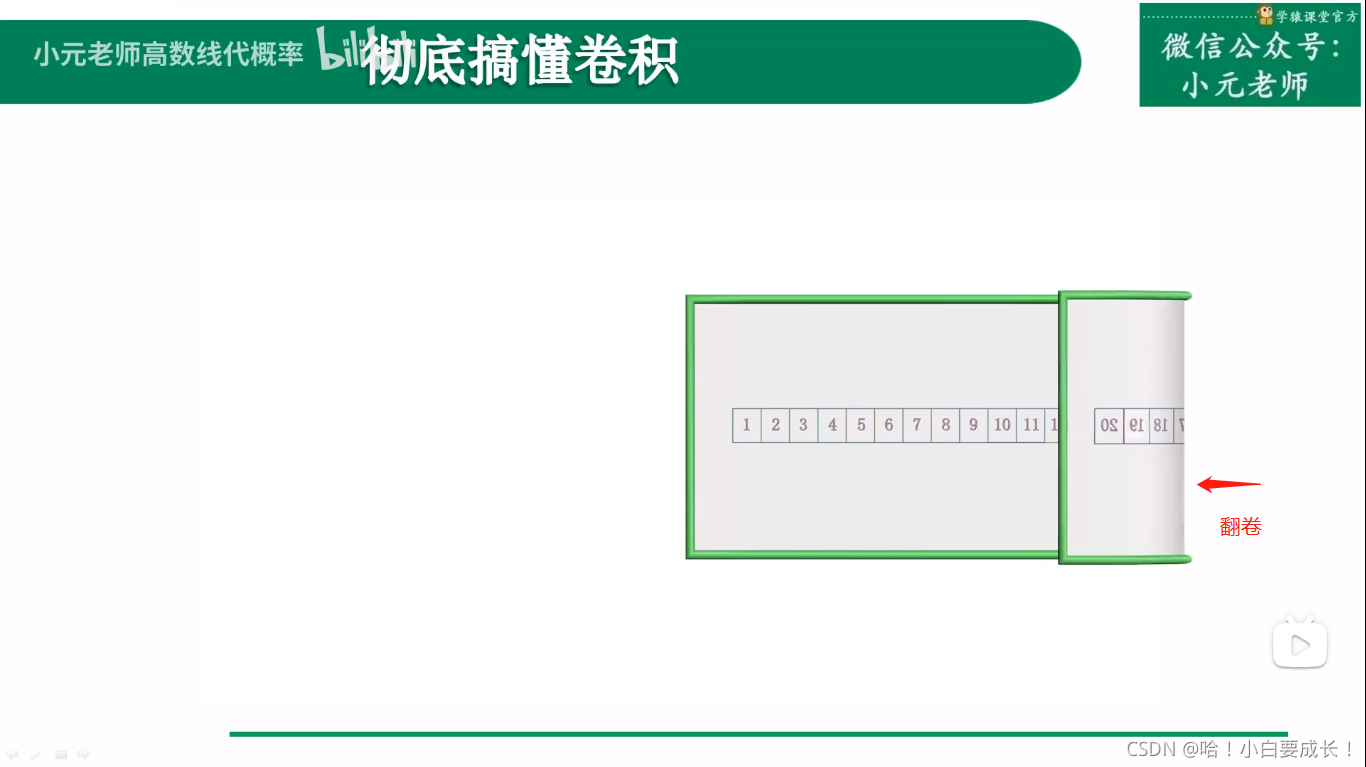

3、卷积过程总结
1.卷积
2.对齐
3.计算卷积结果(乘积求和)
4.平移
5.重复3、4,直到计算出所有点的离散卷积结果
第二种解释
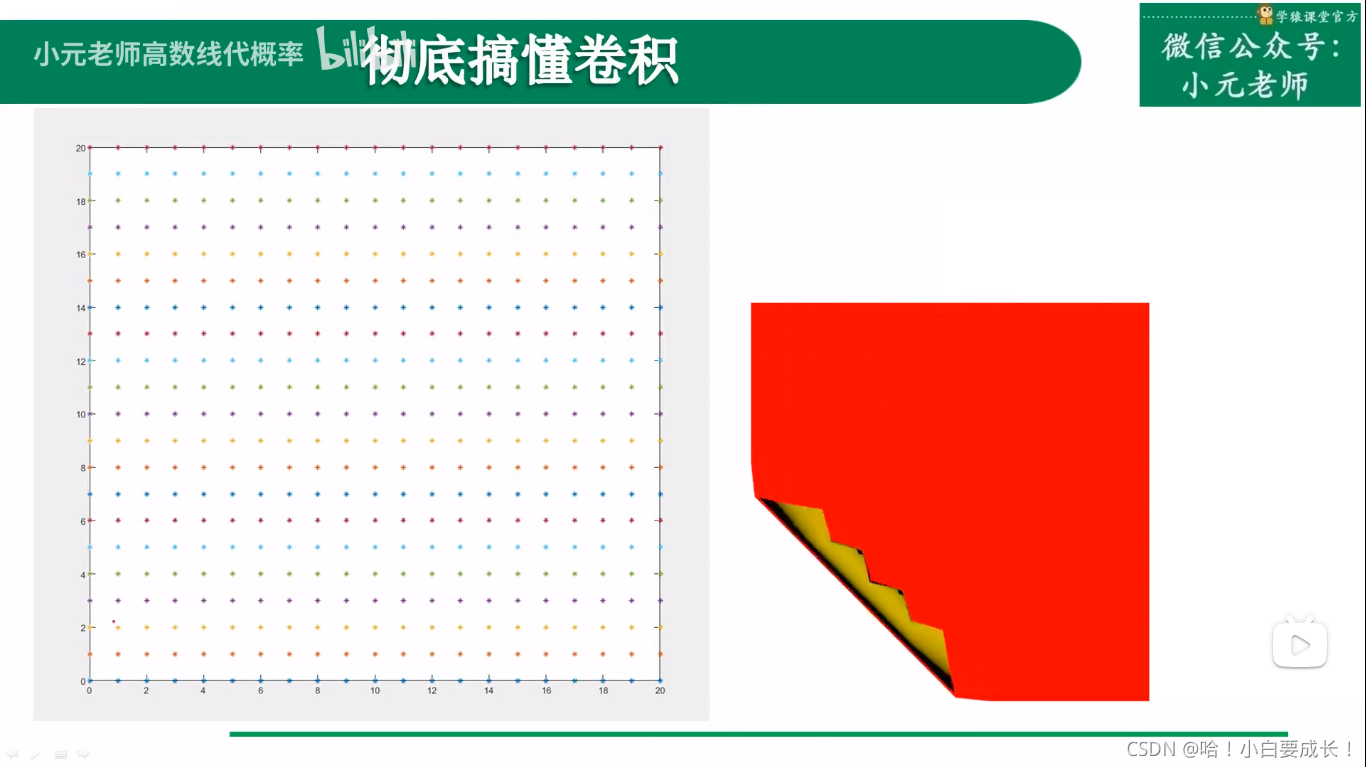
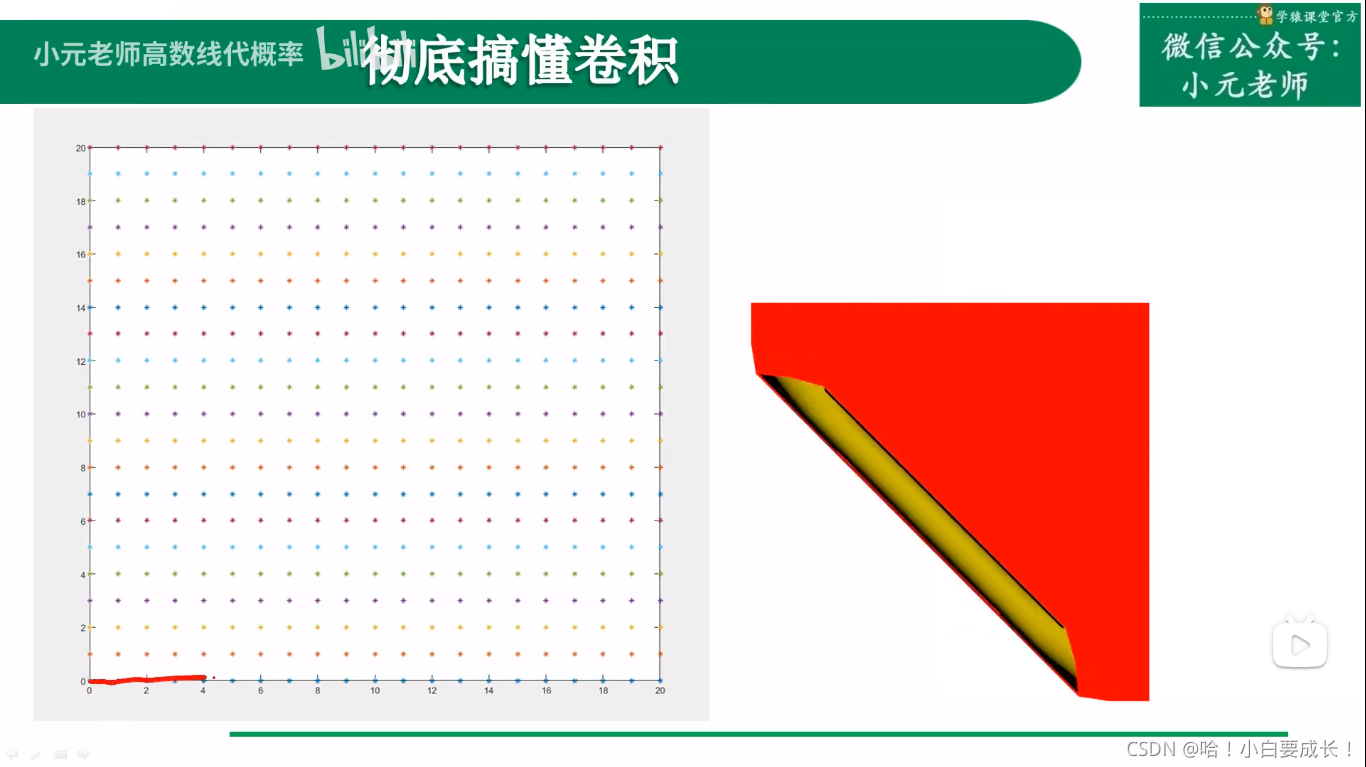

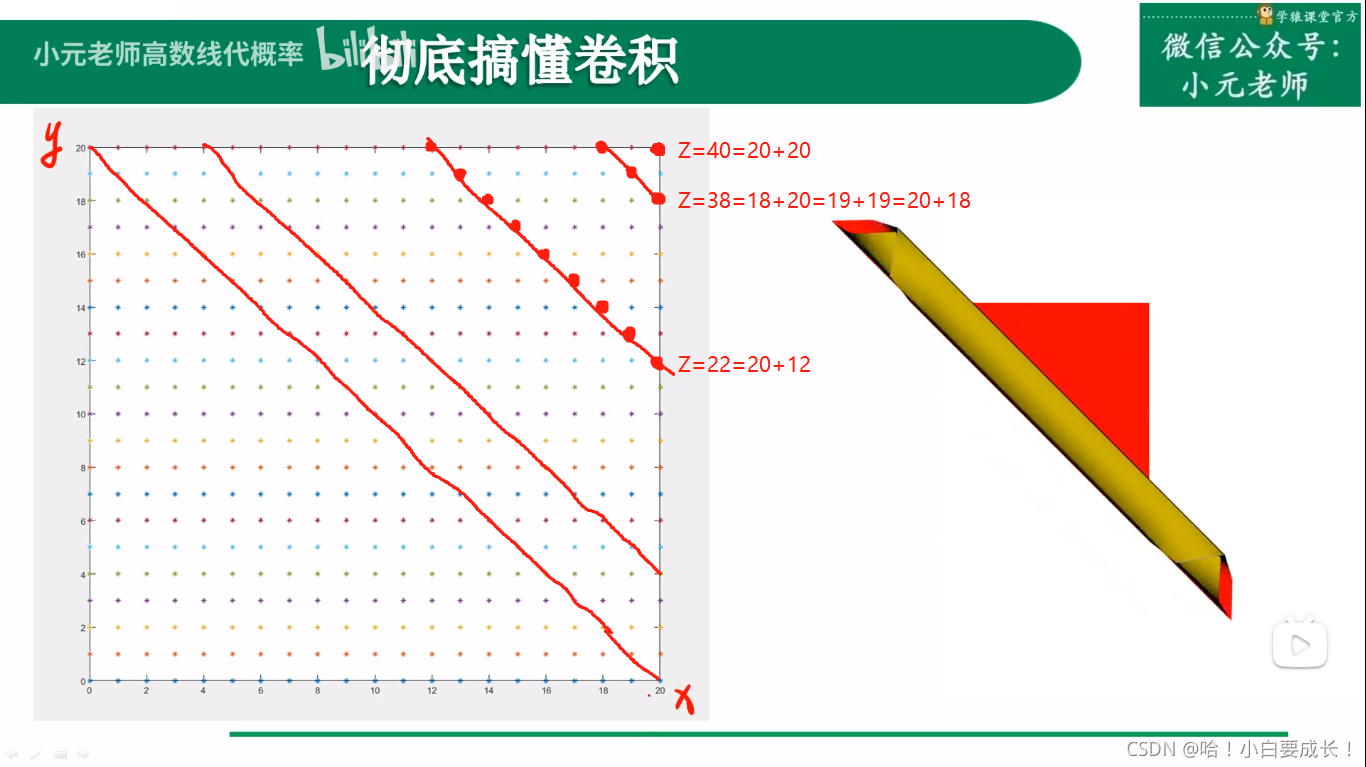
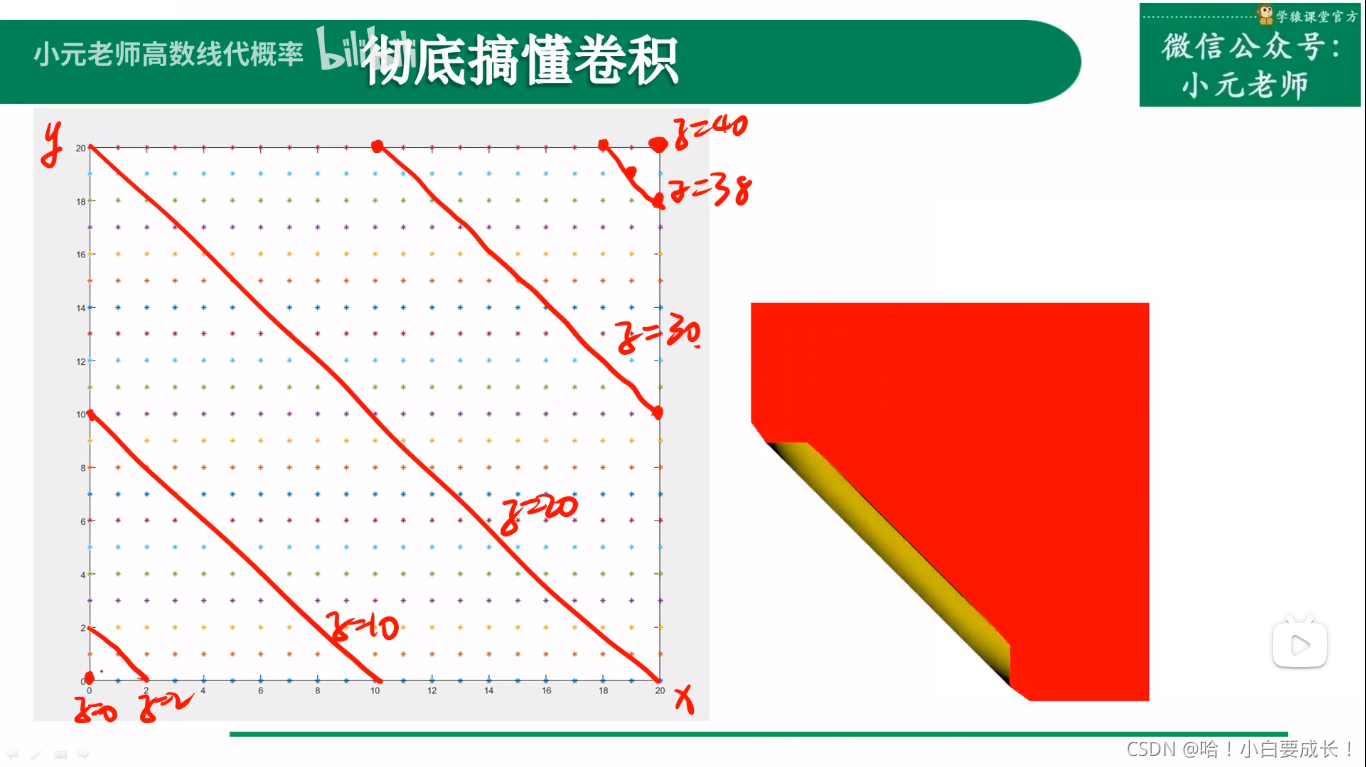
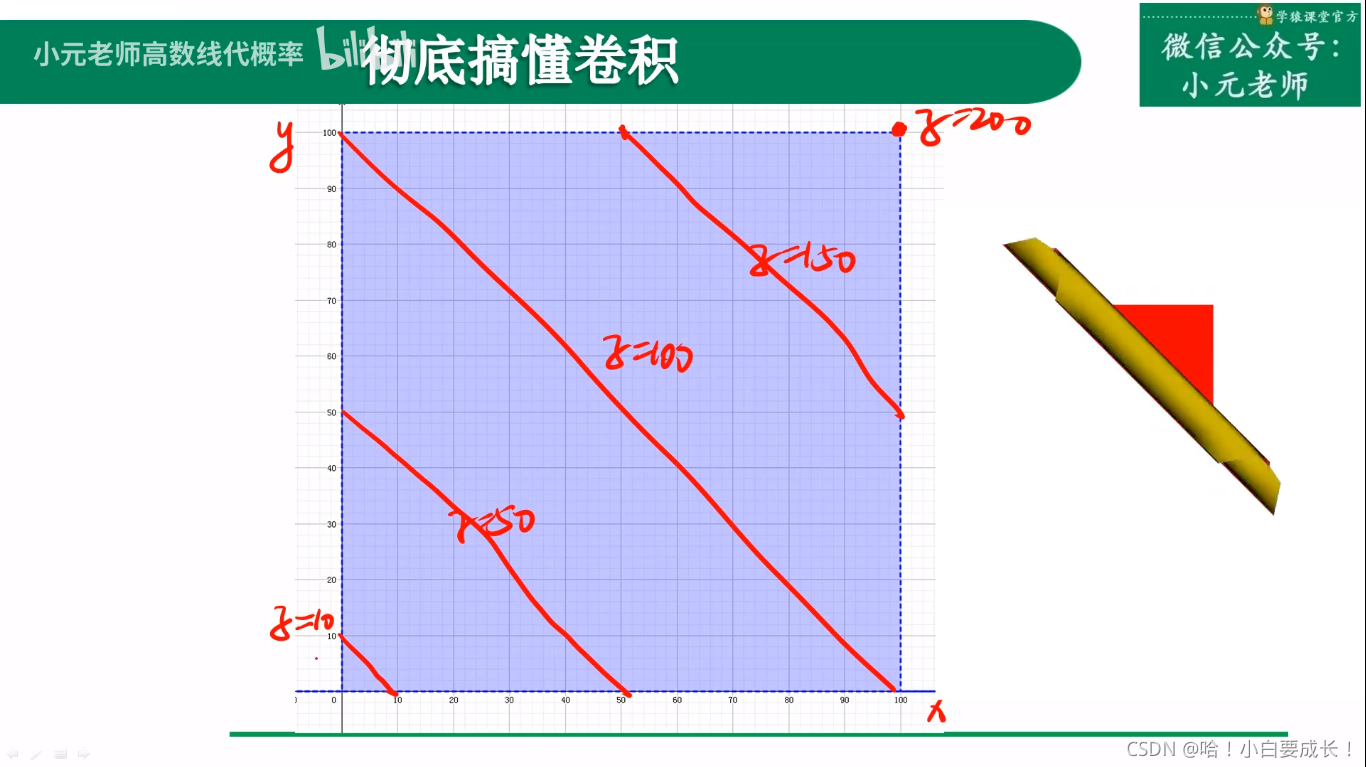
从二维平面上看,这些变化是一个个线条
适用情况
对某一个事物的衡量结果由两个变量共同决定
- x、y决定z
- z决定/衡量事物
二、连续卷积
原来的信号还没有处理完,新的信号又到来了
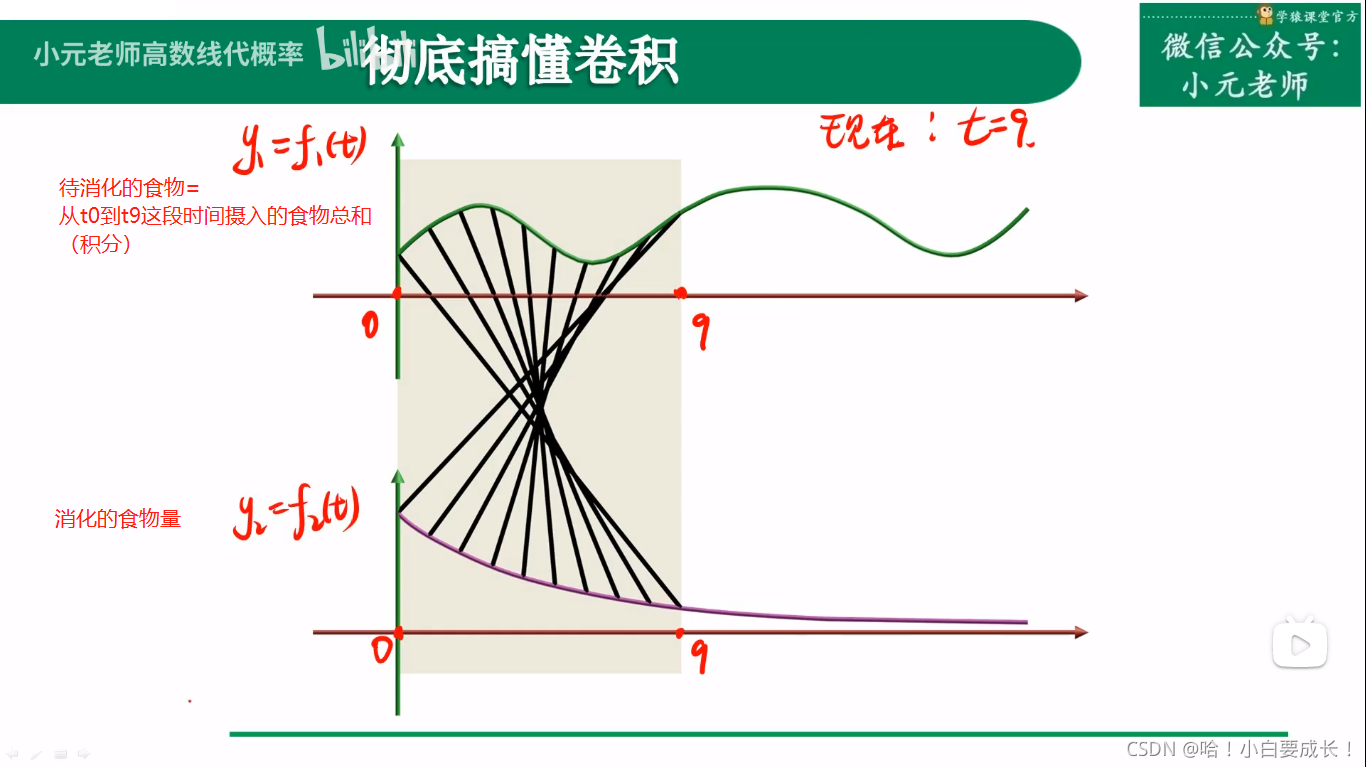
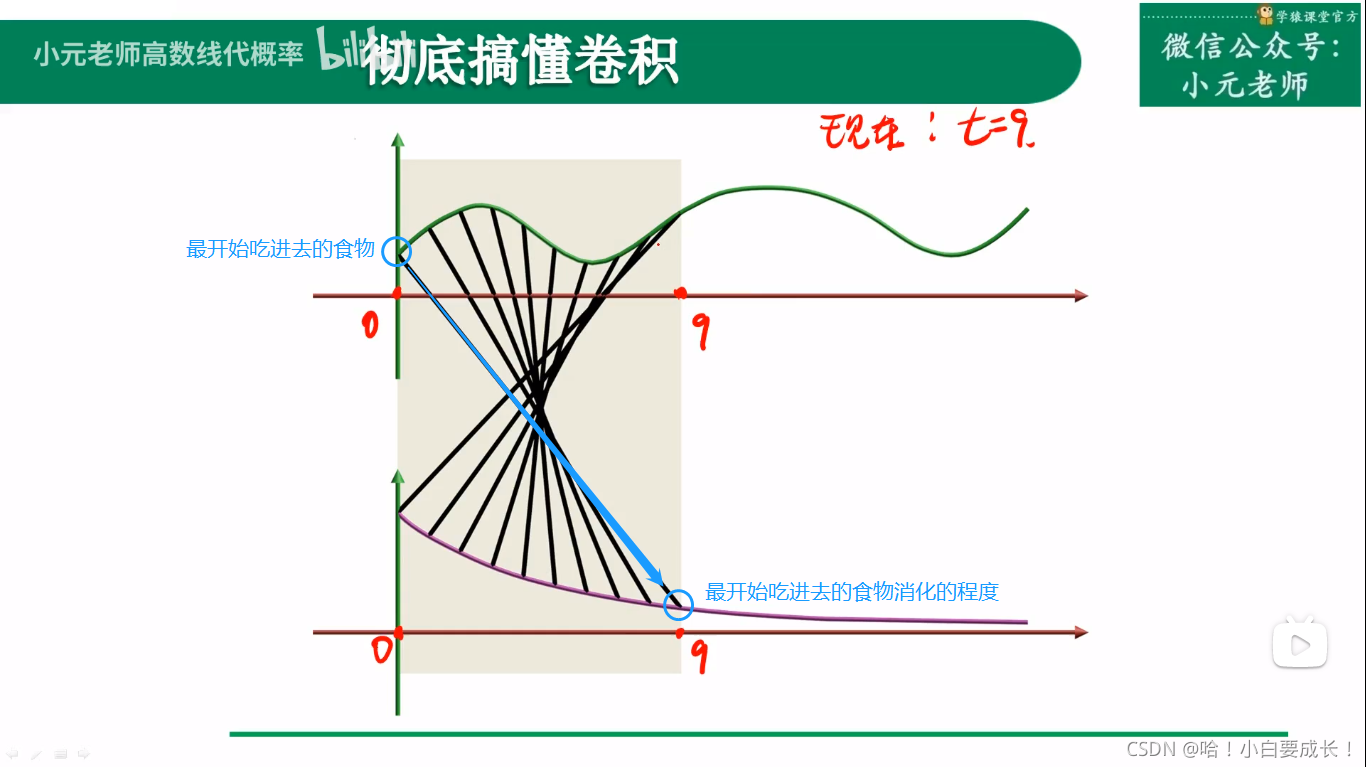
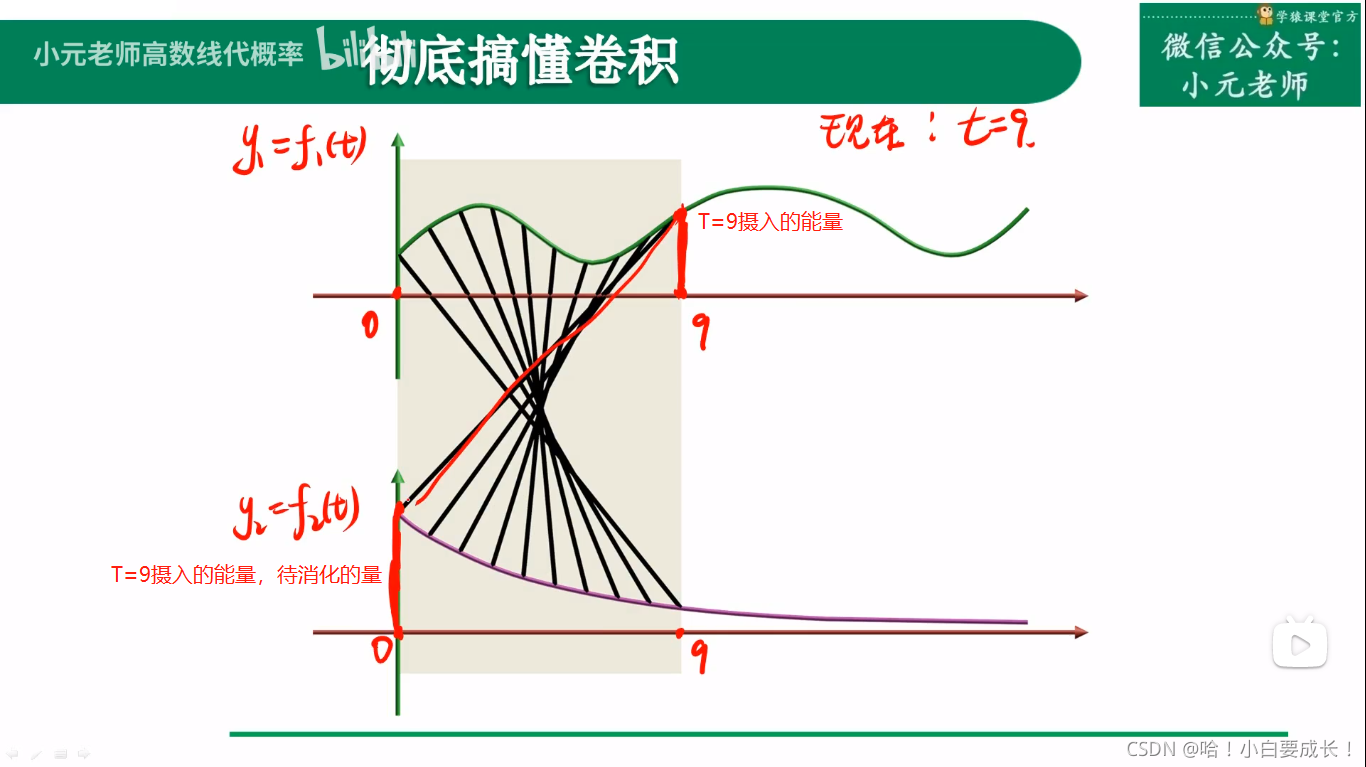

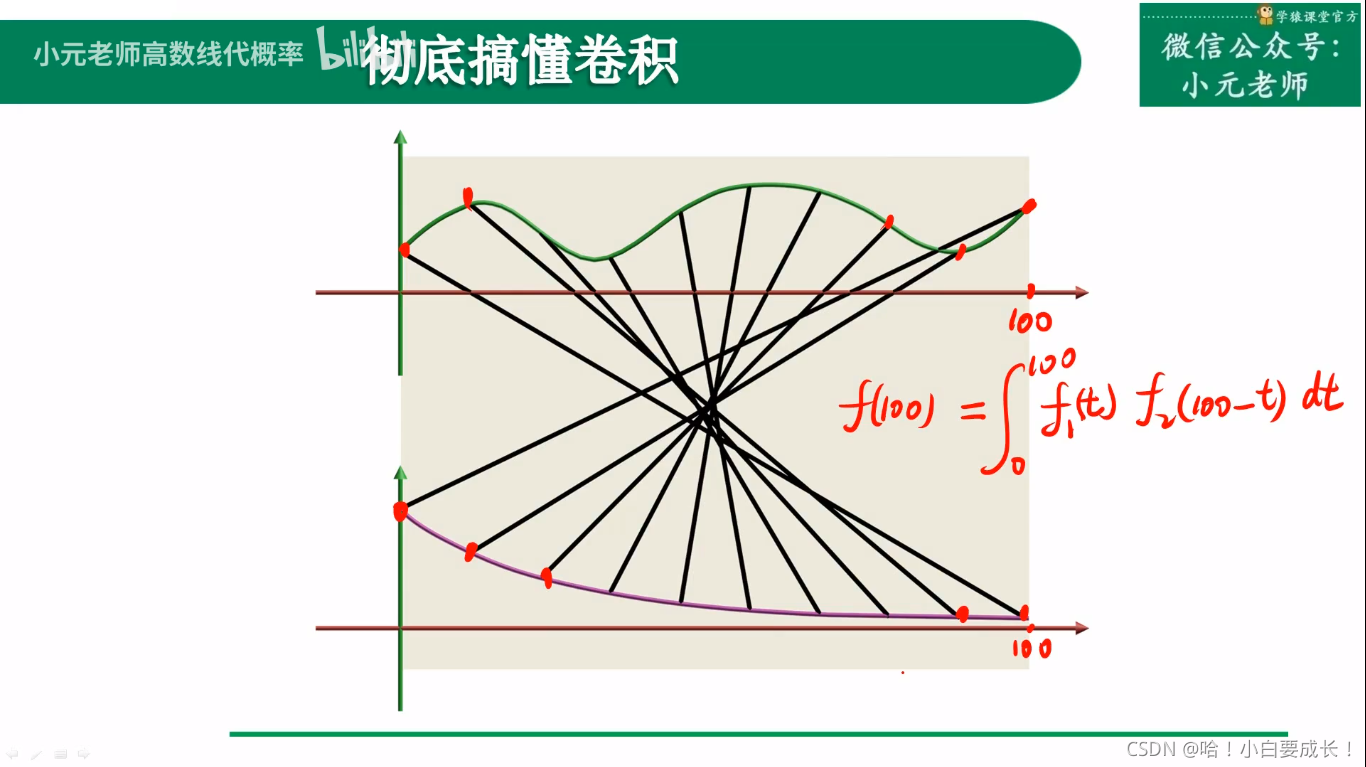
f(100) 代表能输出的总能量(食物消化后转化成的能量)??


卷积过程
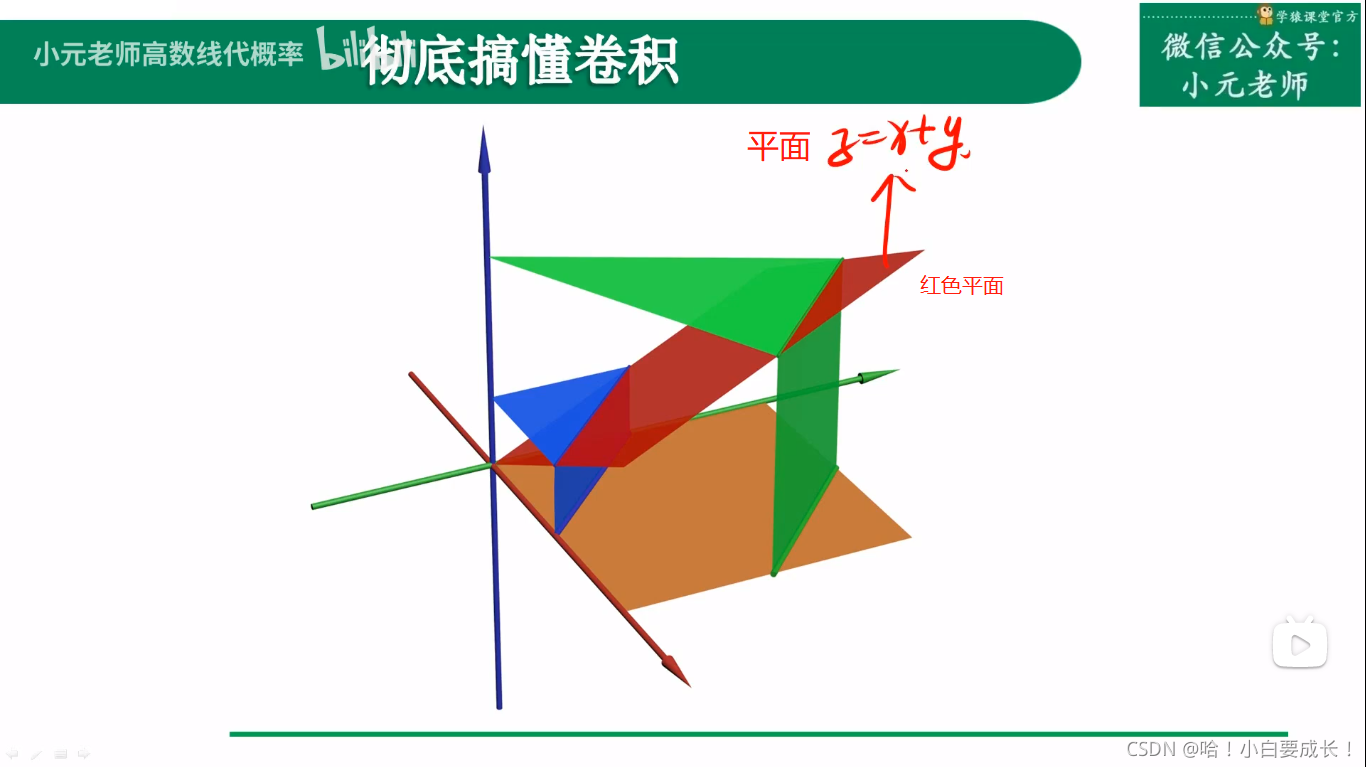
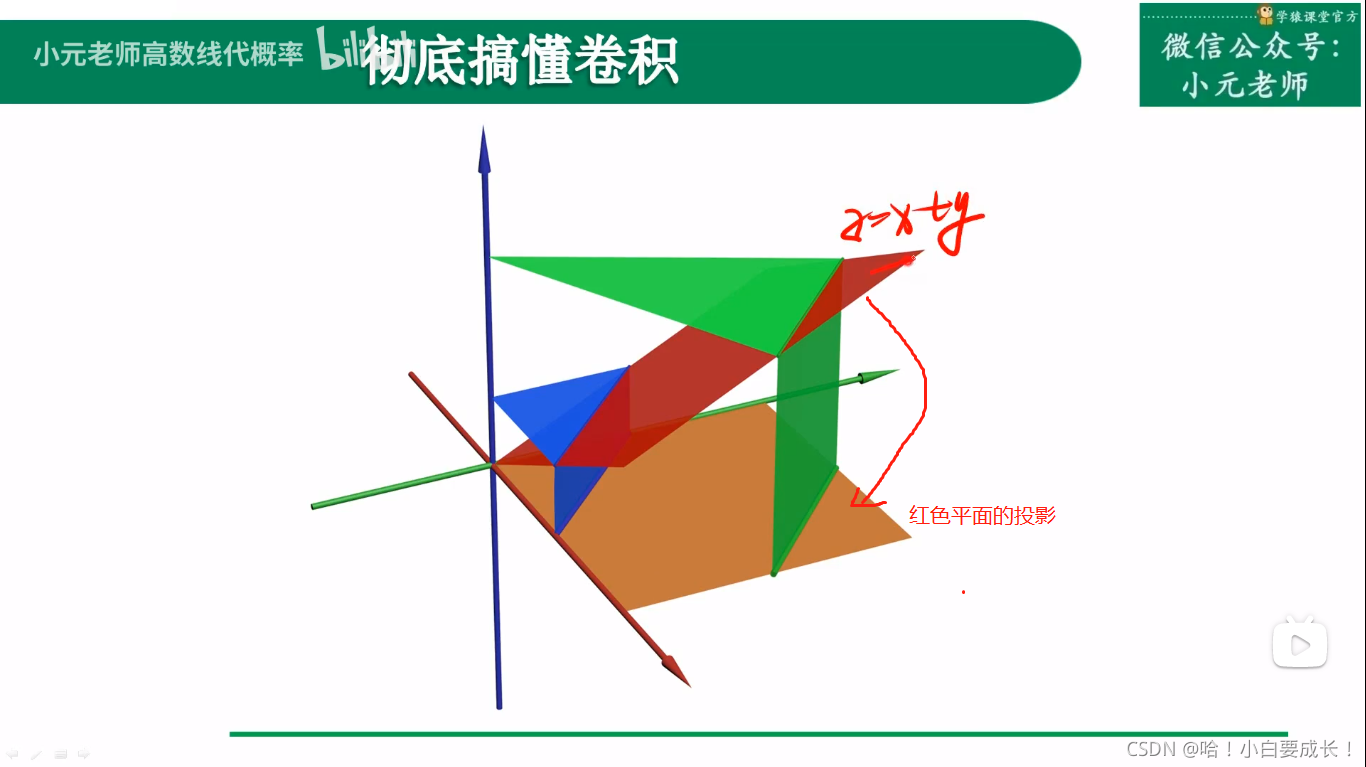
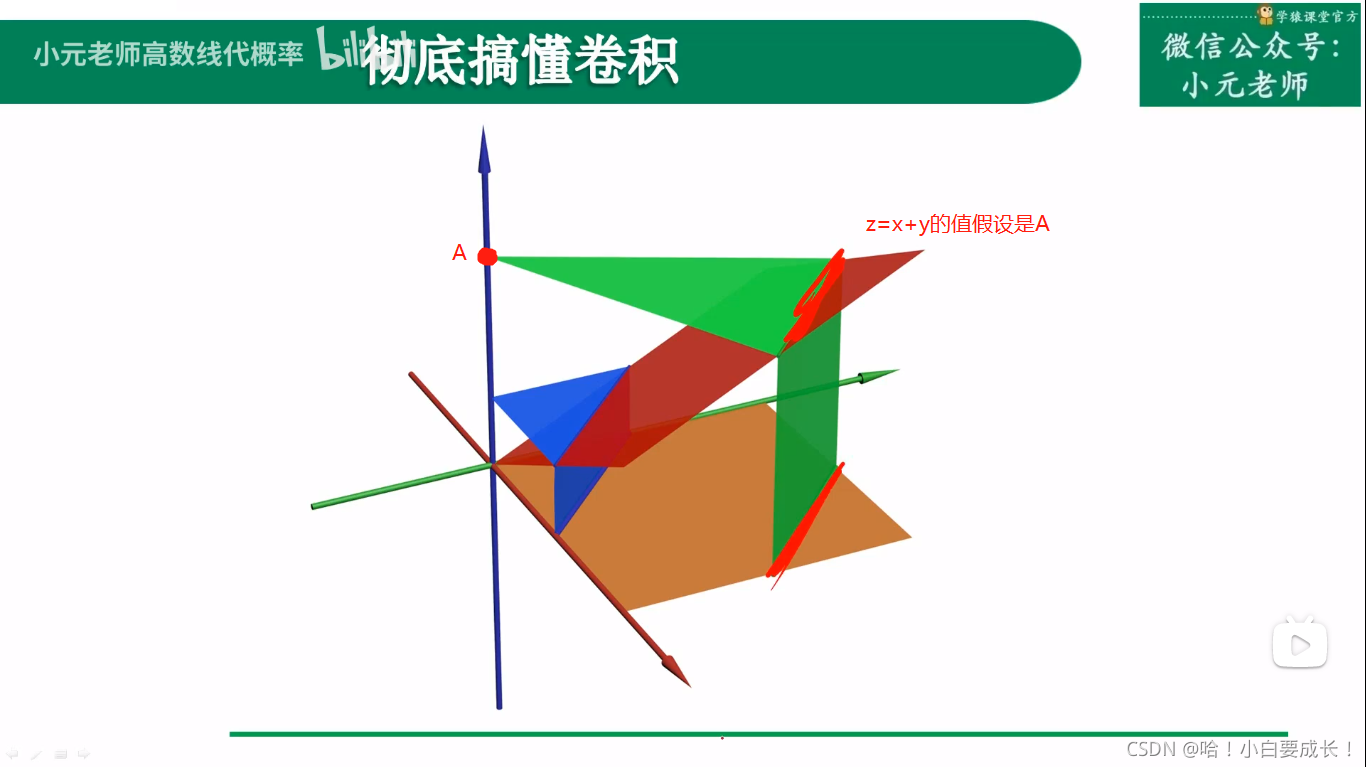
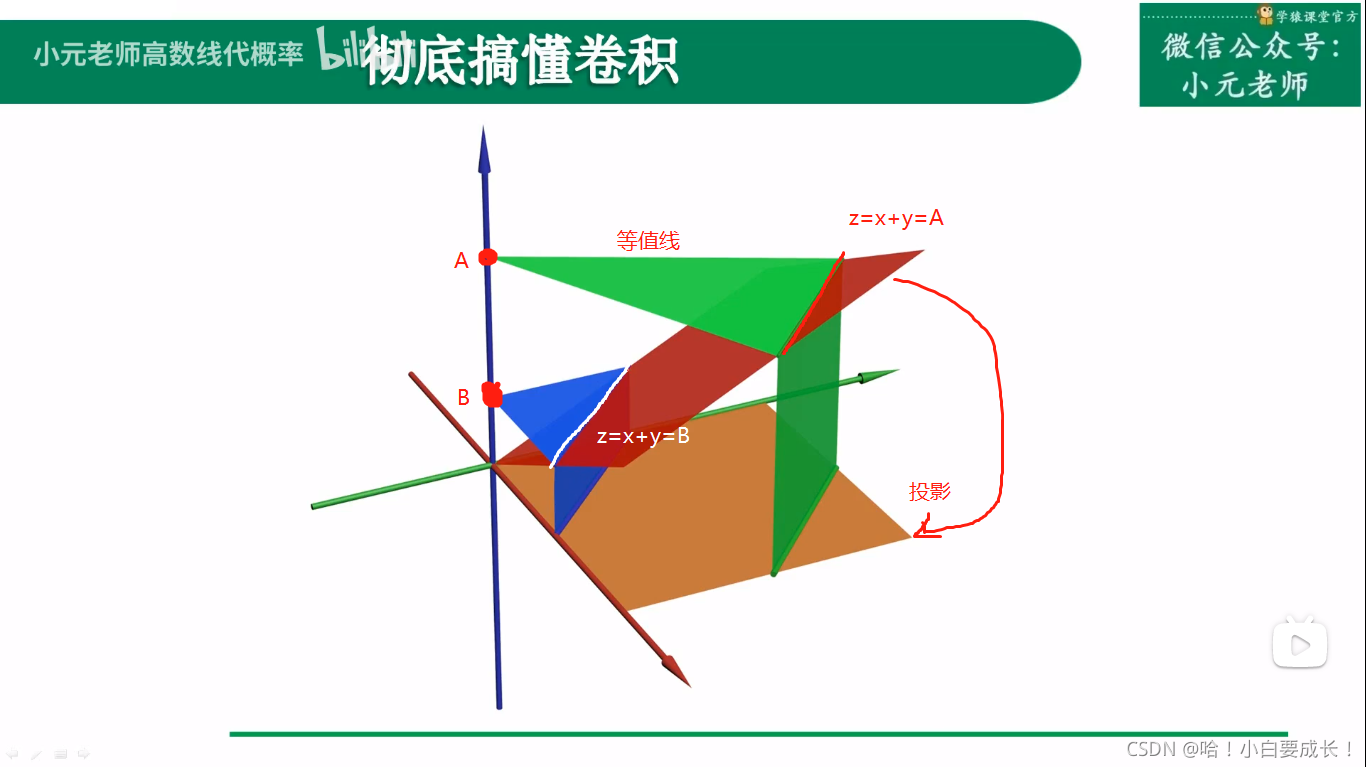
在三维空间里卷积
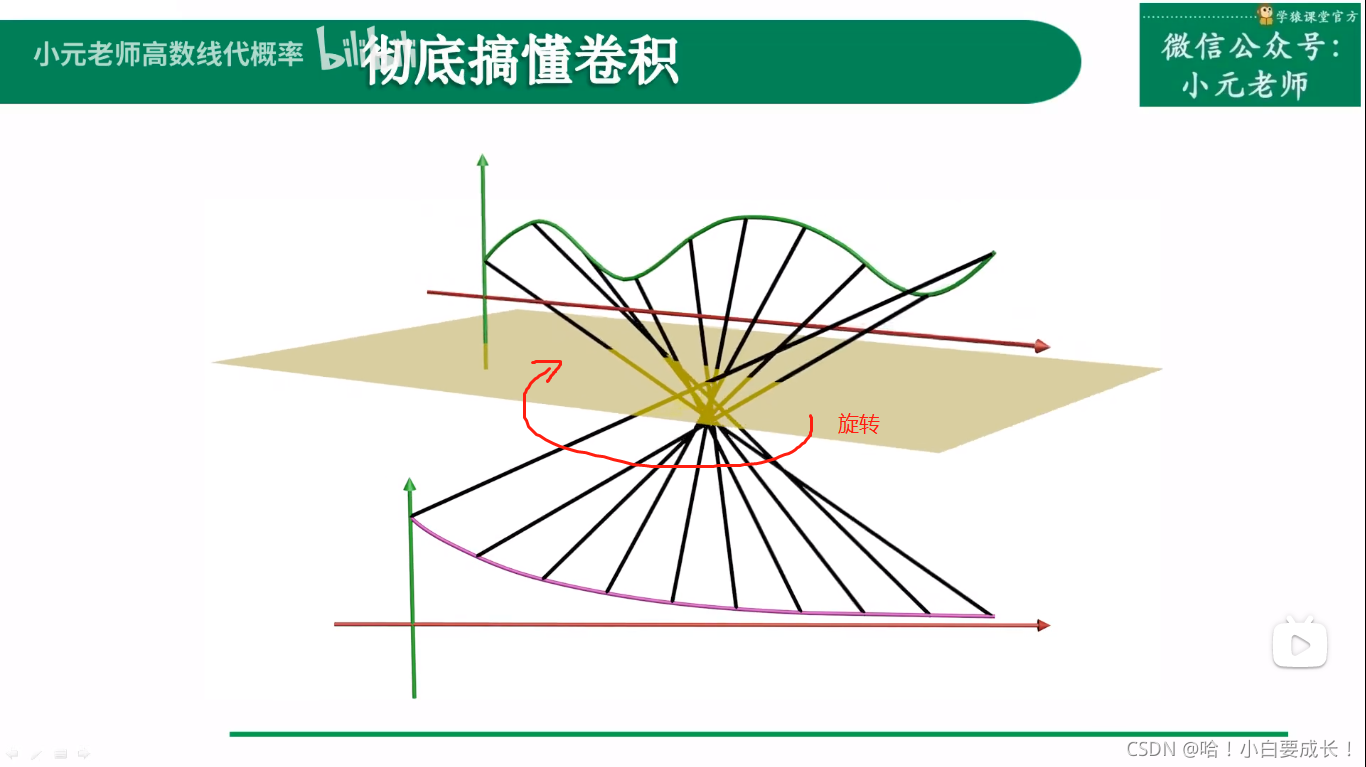
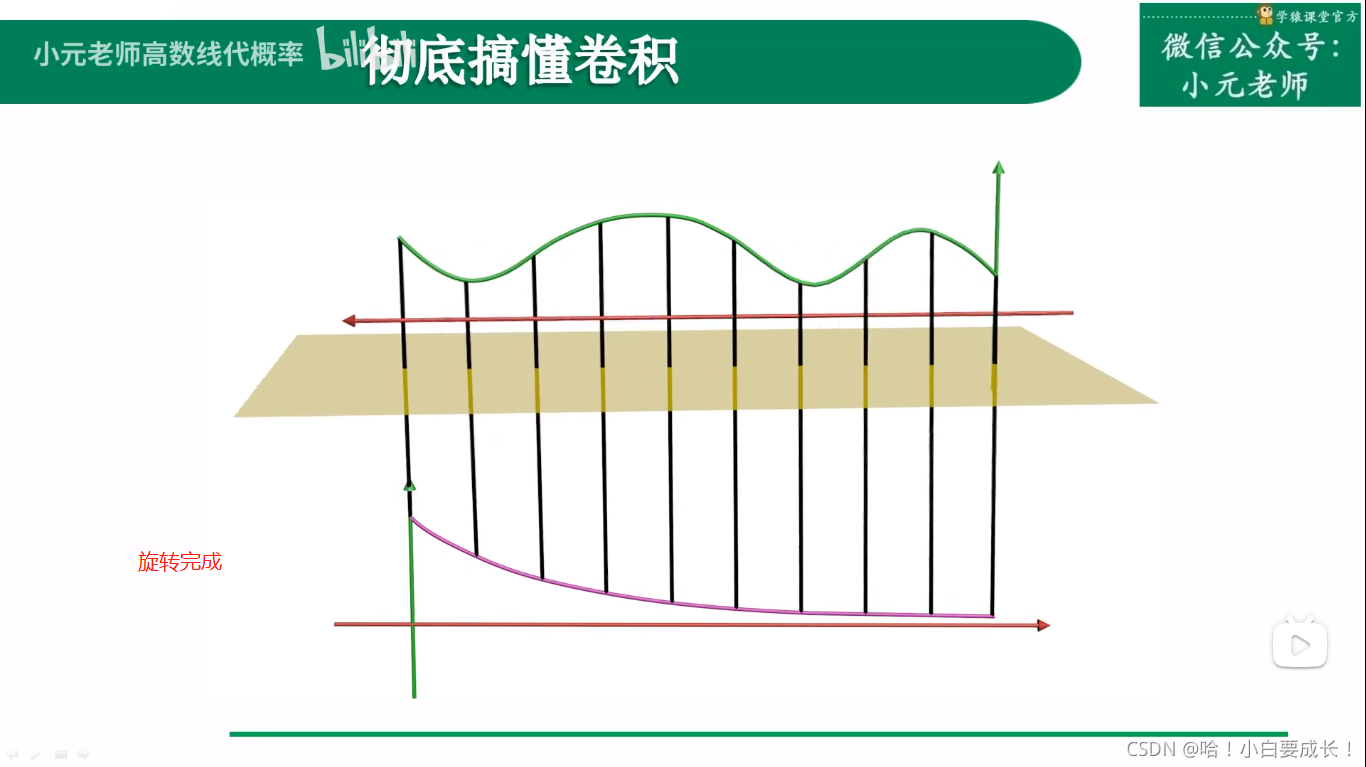
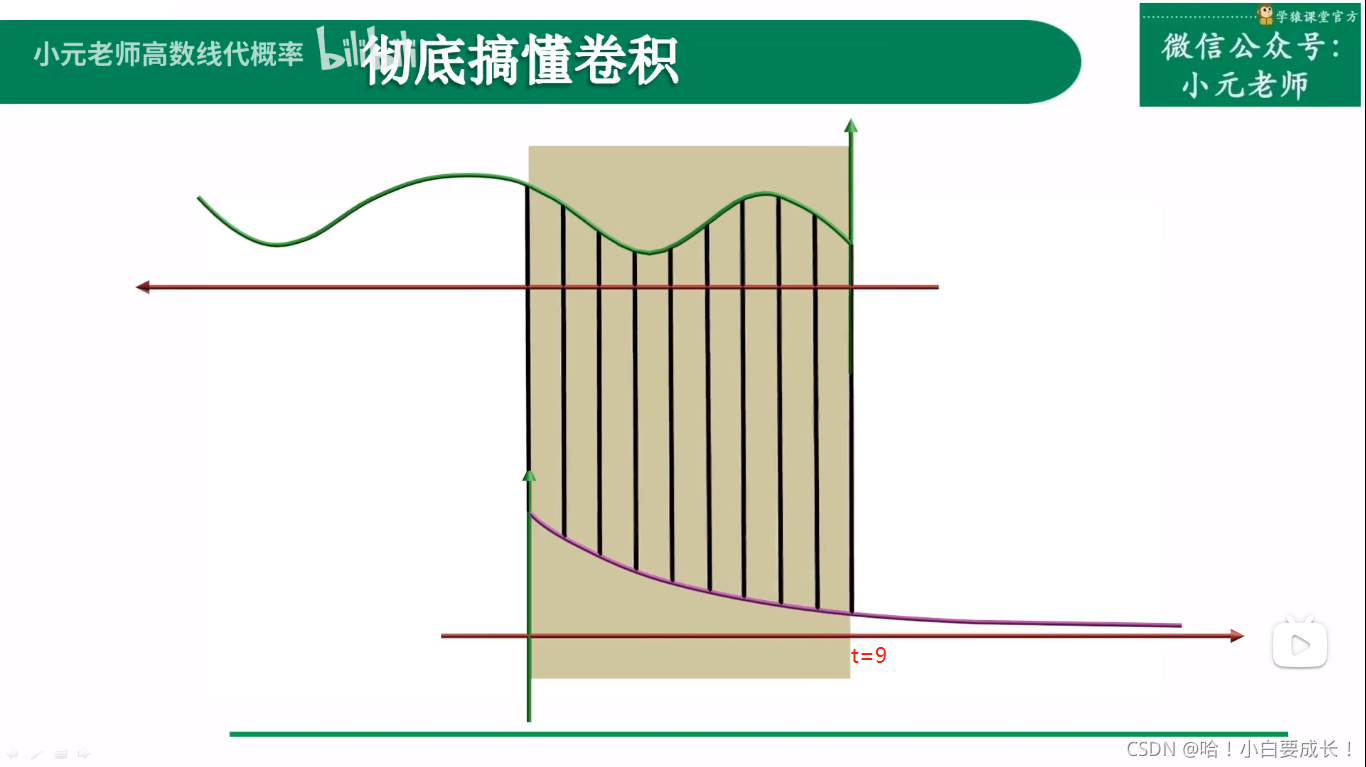
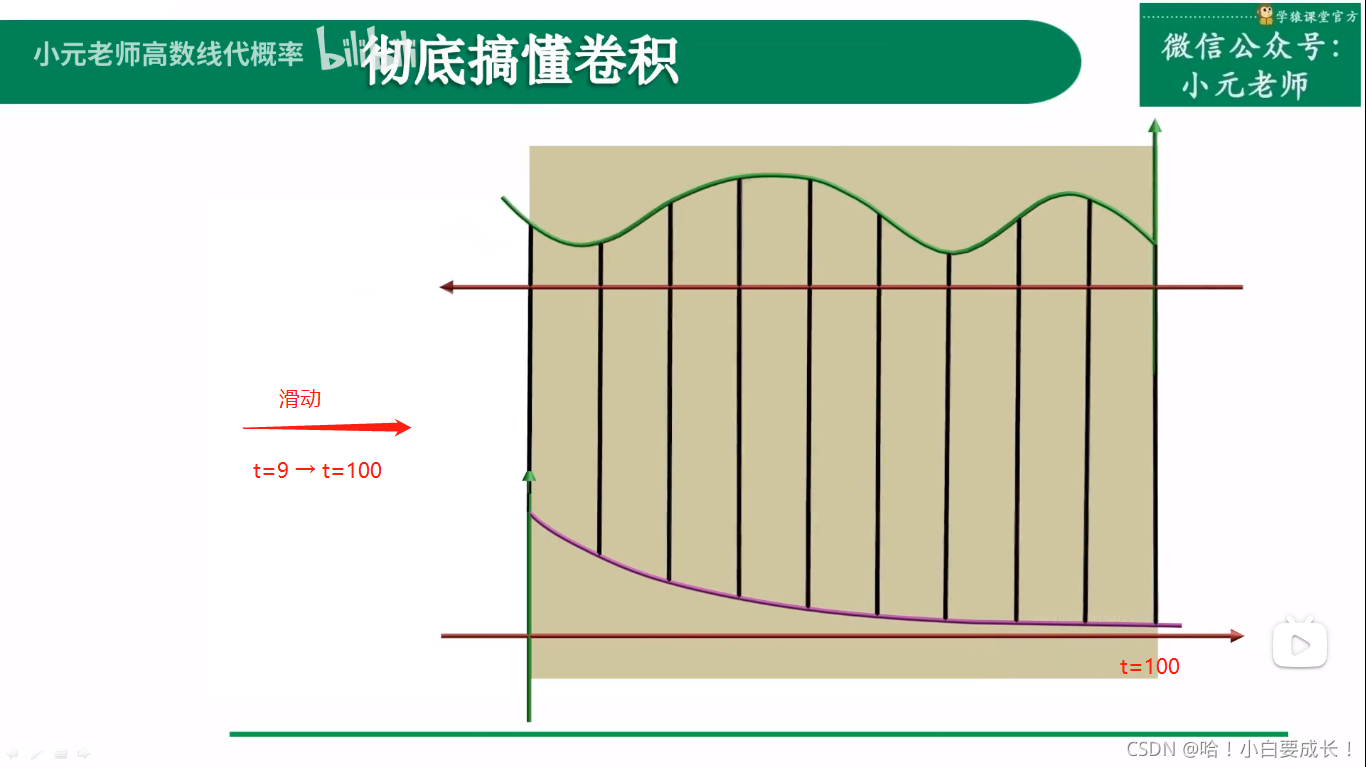
过程
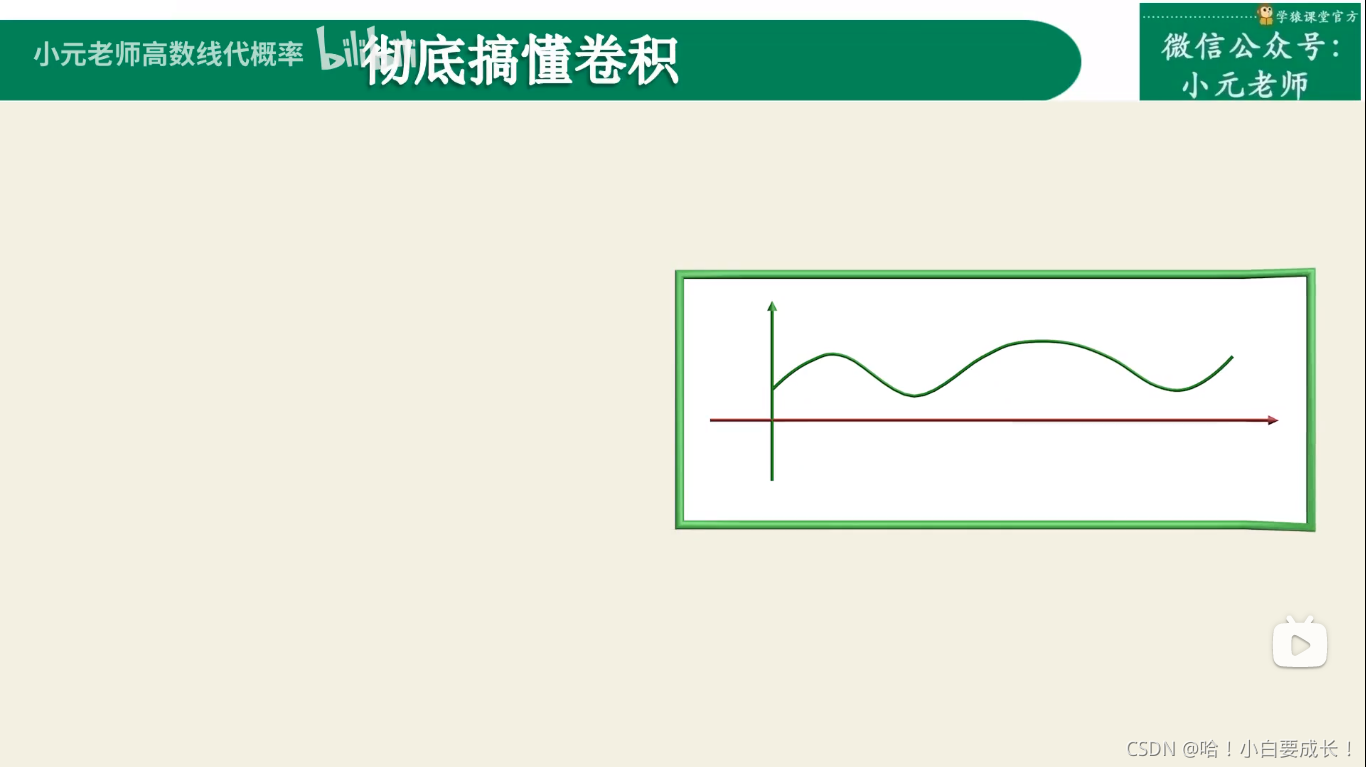
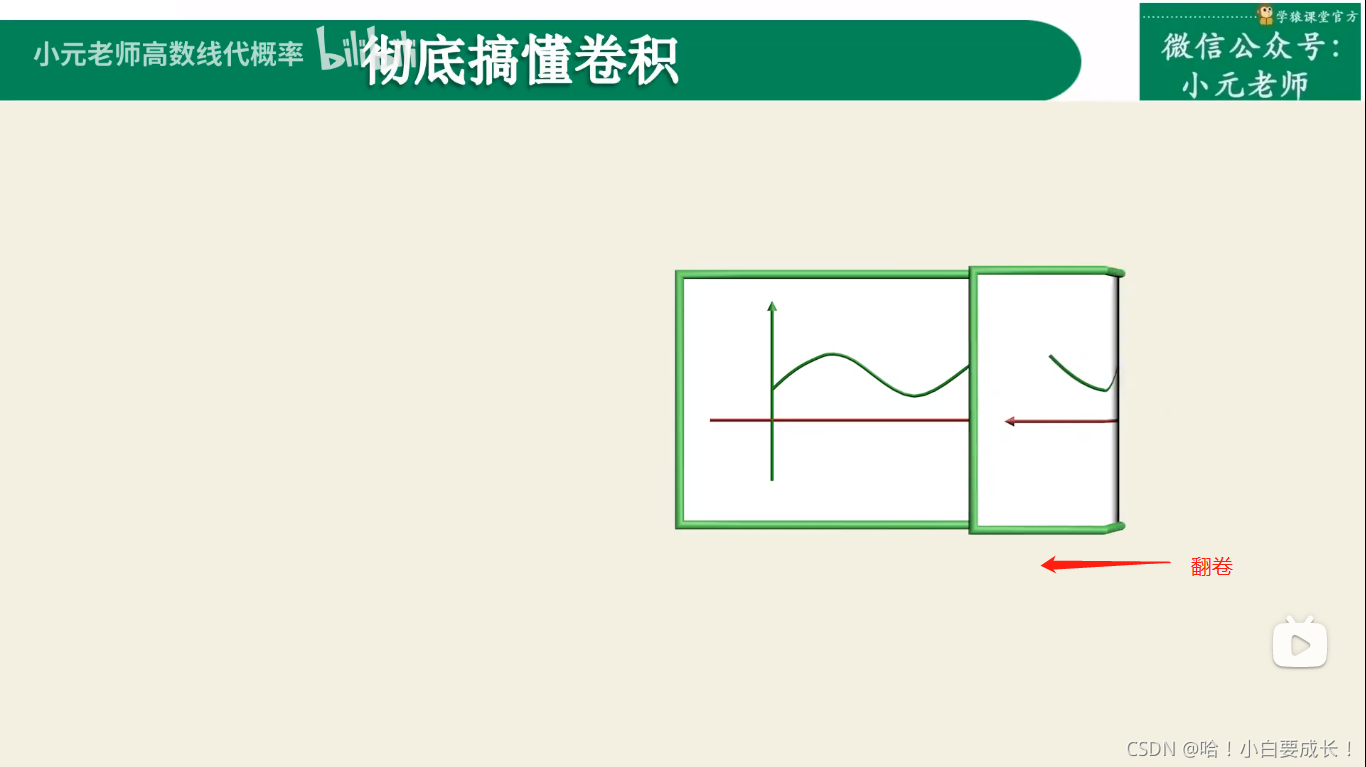
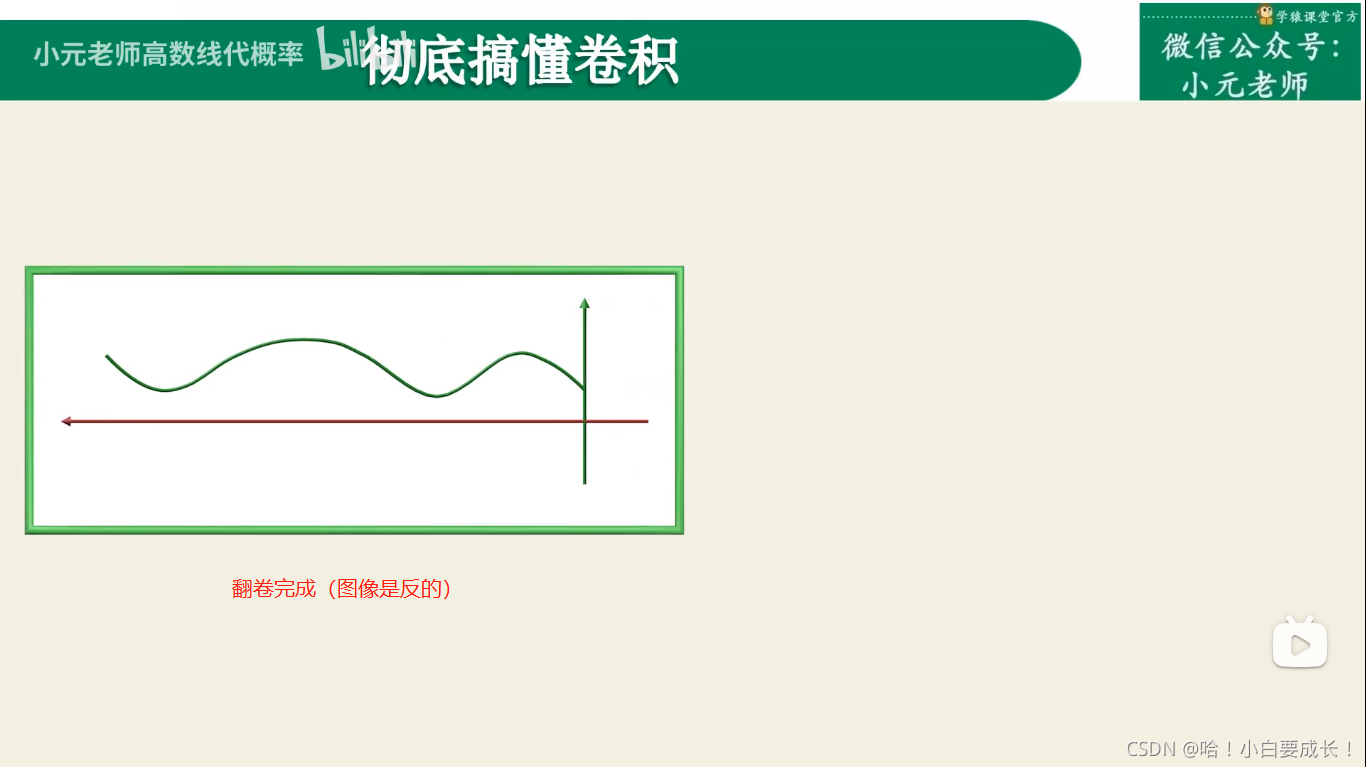

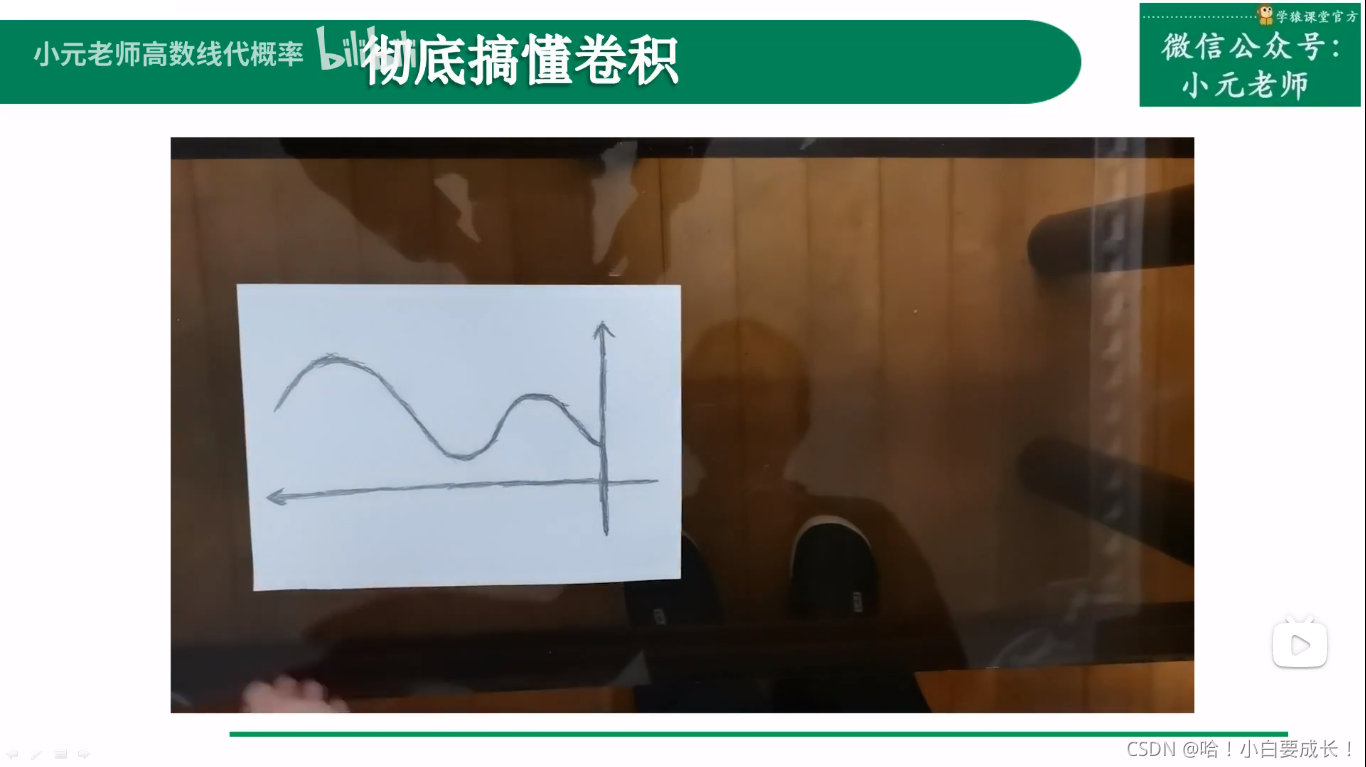
1.卷褶
2.平移
3.做乘积,积分
4.重复2、3,直到计算出所有点的乘积,得到最终积分
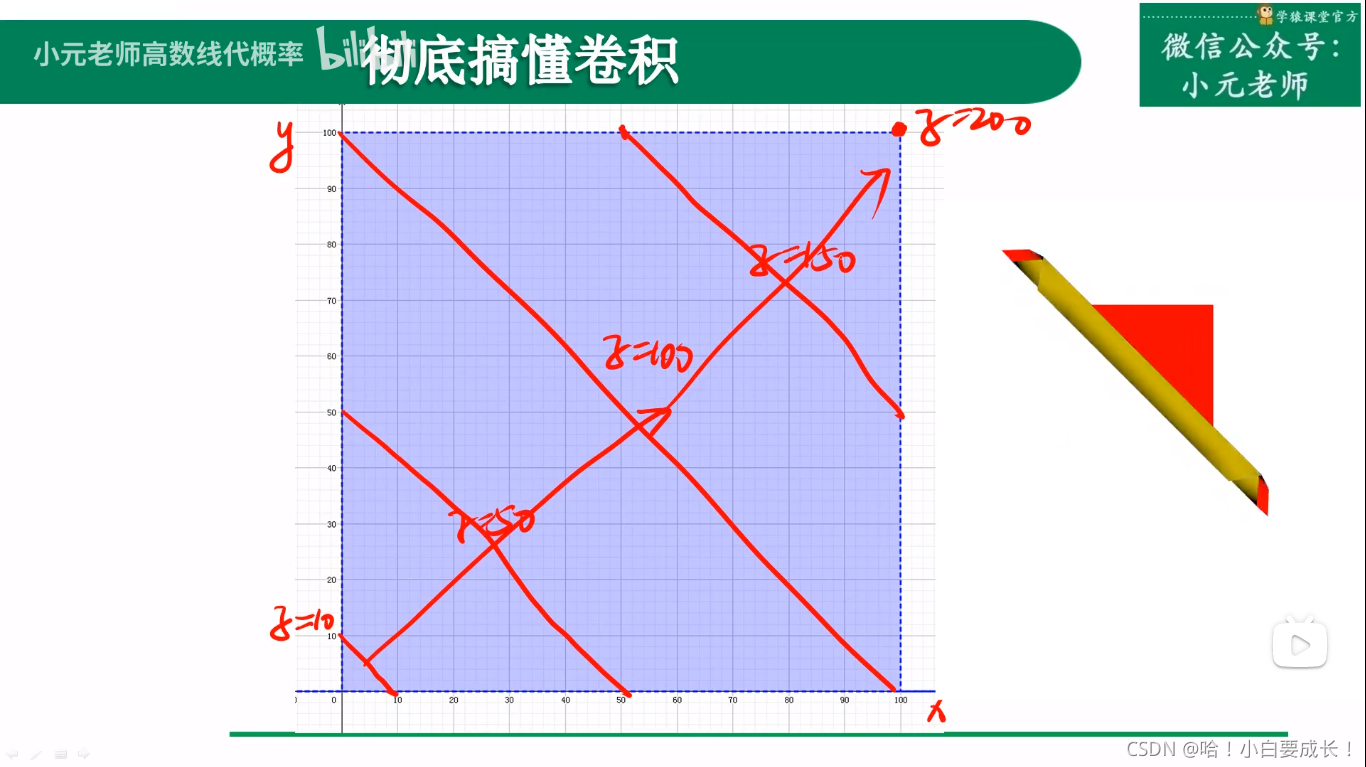
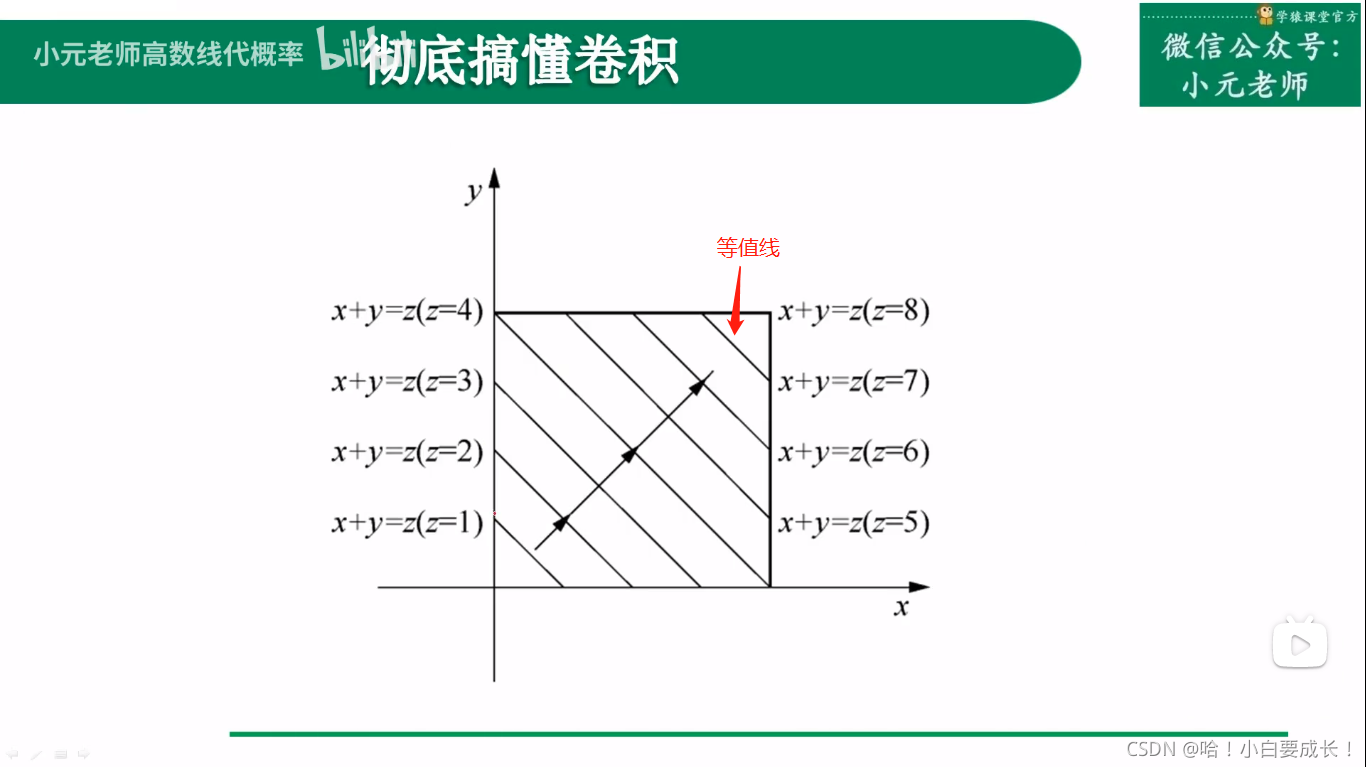
等值线
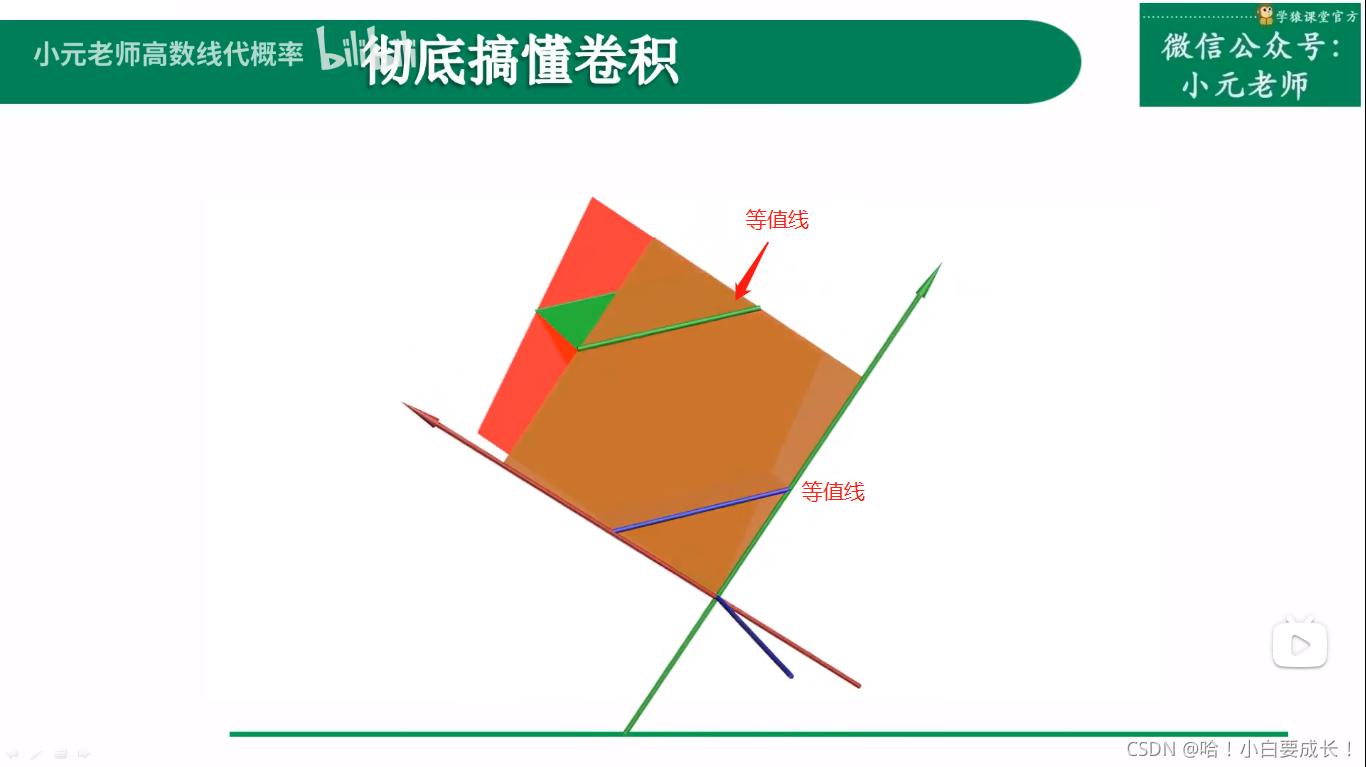
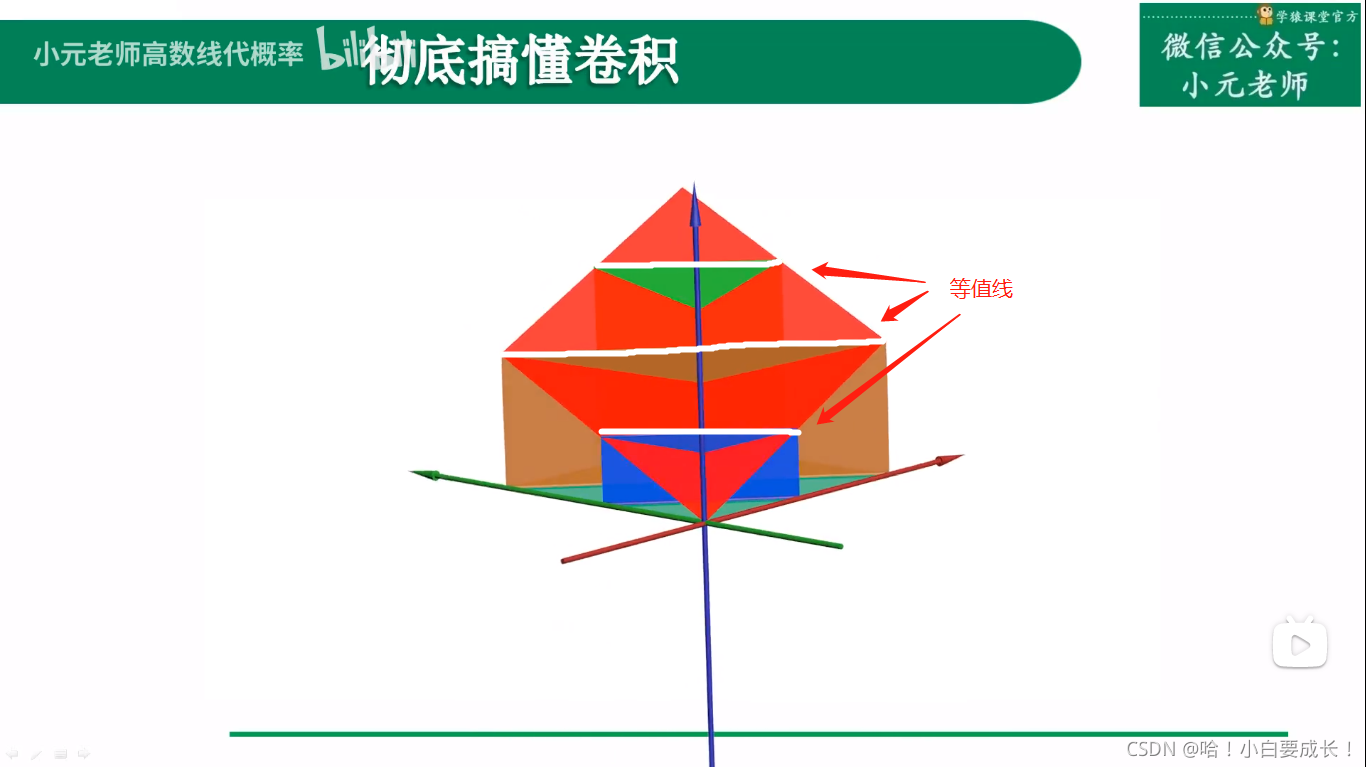
傅里叶

—————————分割线—————————
三、卷积在深度学习神经网络中的应用
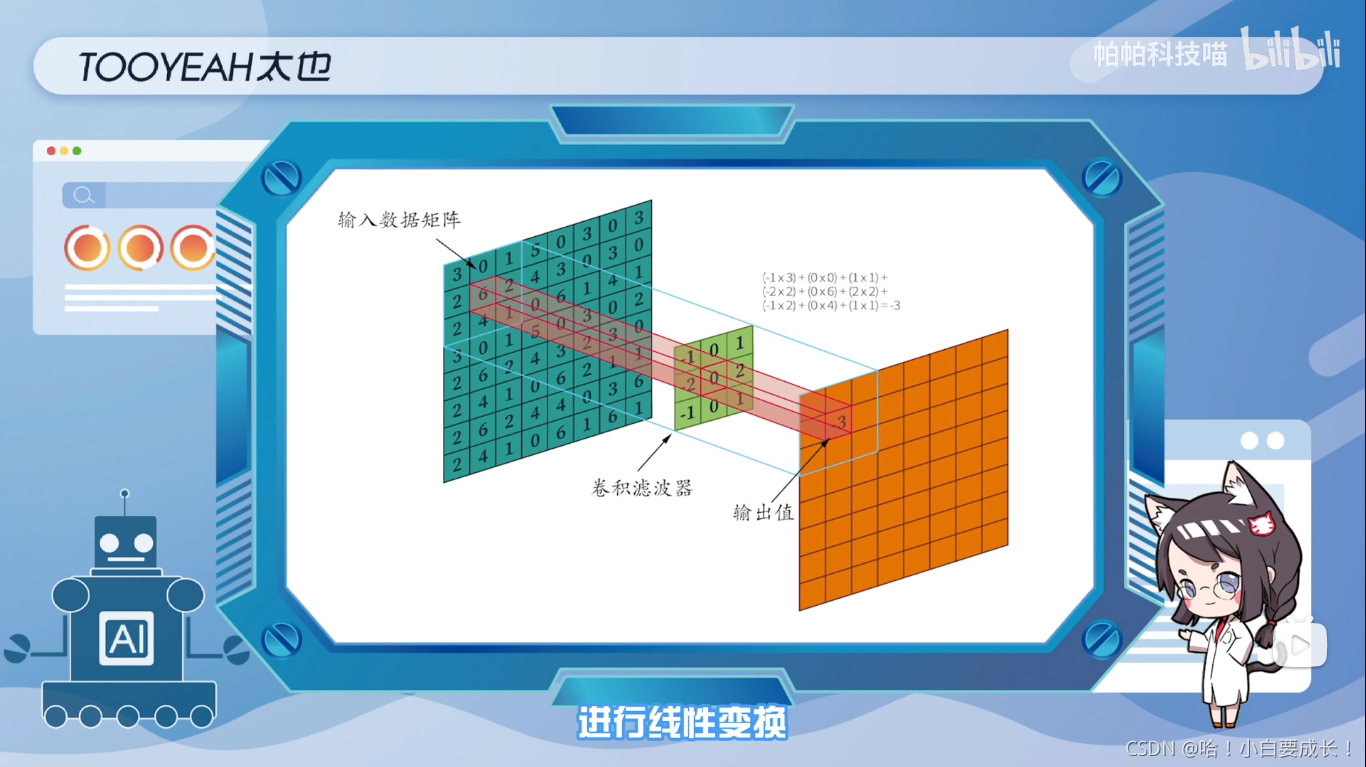
在深度学习神经网络方面,卷积可以看作是一个带有可学习参数的滤波器矩阵或向量,用于从数据中提取特征、从函数映射或变换的角度,卷积过程是在图像(特征矩阵)的每个位置进行线性变换映射成新值的过程。
将卷积核看成权重,记为w,图像对应位置的像素即为x,则该位置的卷积结果为y=w’x+b。
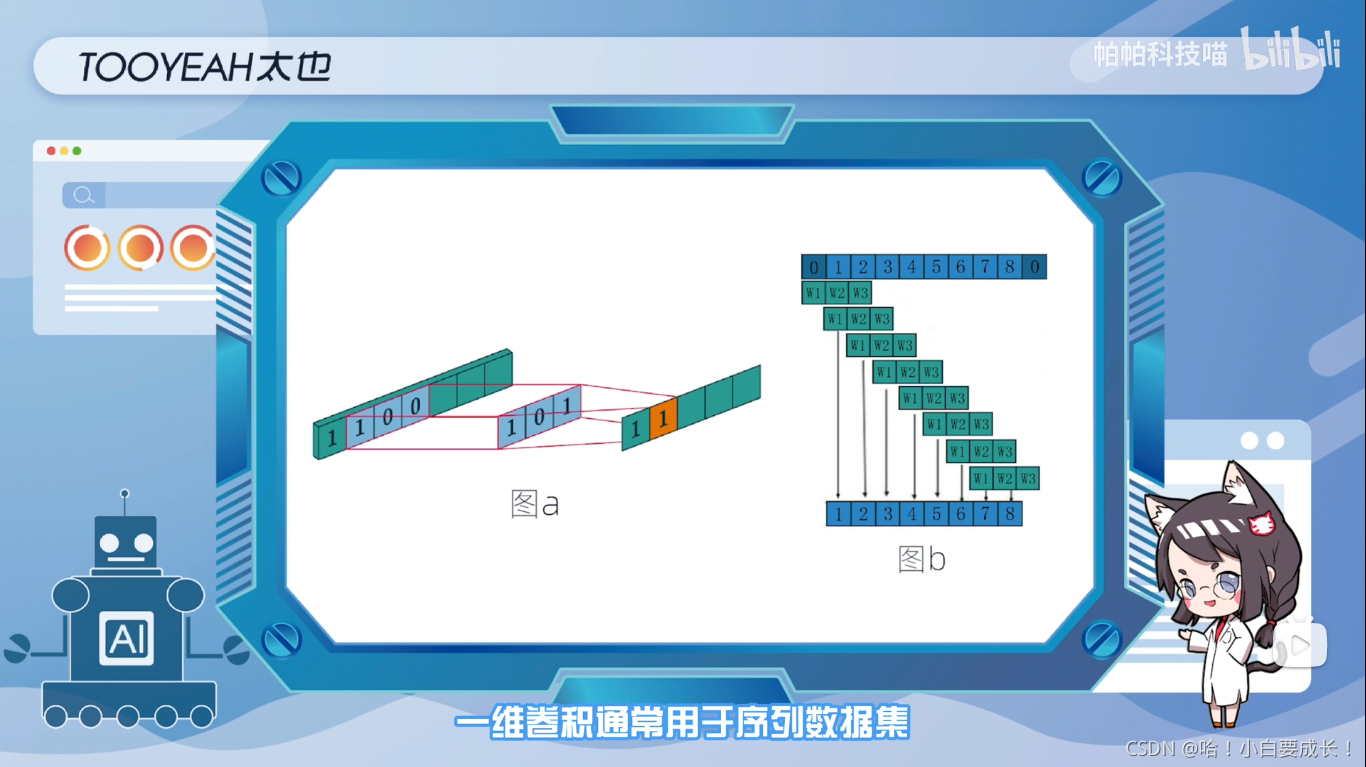
一维卷积
一维卷积通常用于序列数据集,可以从输入序列中提取局部1D(一维)子序列,并在卷积窗口中识别局部模式。
如图a所示,以一维的卷积滤波器沿着一个方向移动并计算,输入特征向量(1,0,0)与卷积权重(1,0,1)相乘,得到输出1.
而在神经网络中,卷积滤波器的权重是需要通过输入和标签进行运算得到的,如图中的(w1,w2,w3)。
二维卷积
在图像处理领域,卷积神经网络CNN架构中使用的大多是二维卷积滤波器。
二维卷积的主要思想,是通过卷积滤波器向(x,y)两个方向移动,从图像数据中计算出低维特征,其输出形状也是一个二维矩阵。
二维卷积可以分为单通道卷积和多通道卷积
单通道卷积
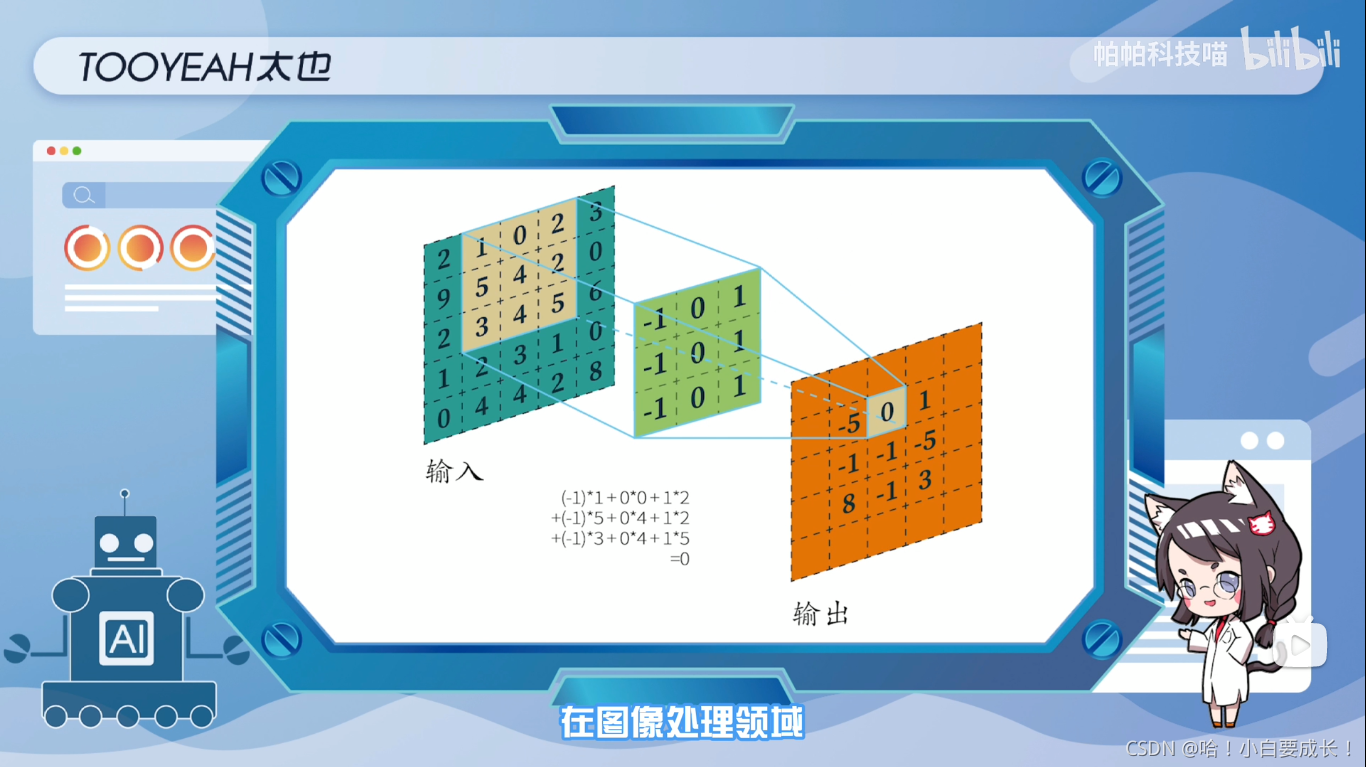
在深度学习中,卷积是元素先乘法后加法,对于具有单个通道的图像卷积如图所示,这里的滤波器是一个3x3的矩阵,元素为:[ [0,1,2], [2,2,0], [0,1,2] ]。
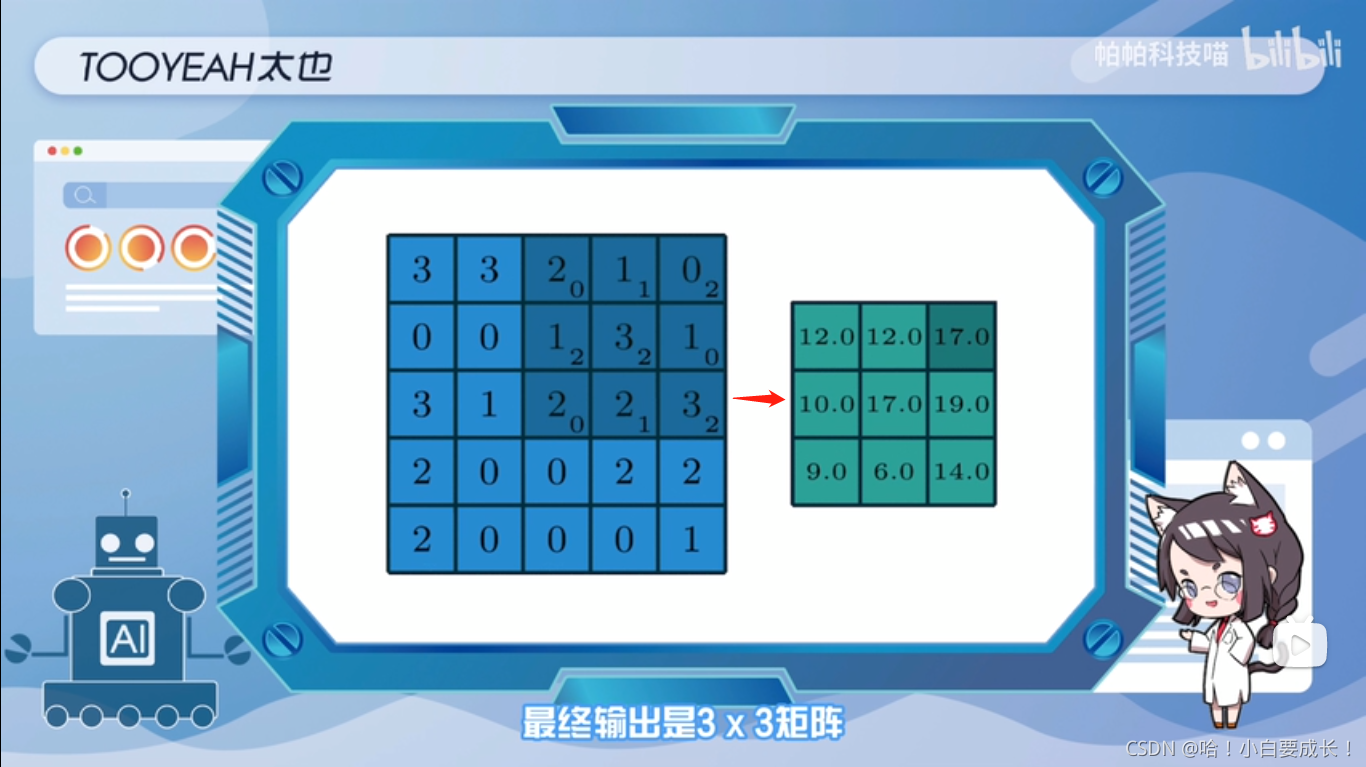
过滤器在输入端滑动,在每个位置,它都在进行元素乘法和加法每个滑动位置最终都有一个数字,最终输出是3x3矩阵。
多通道卷积
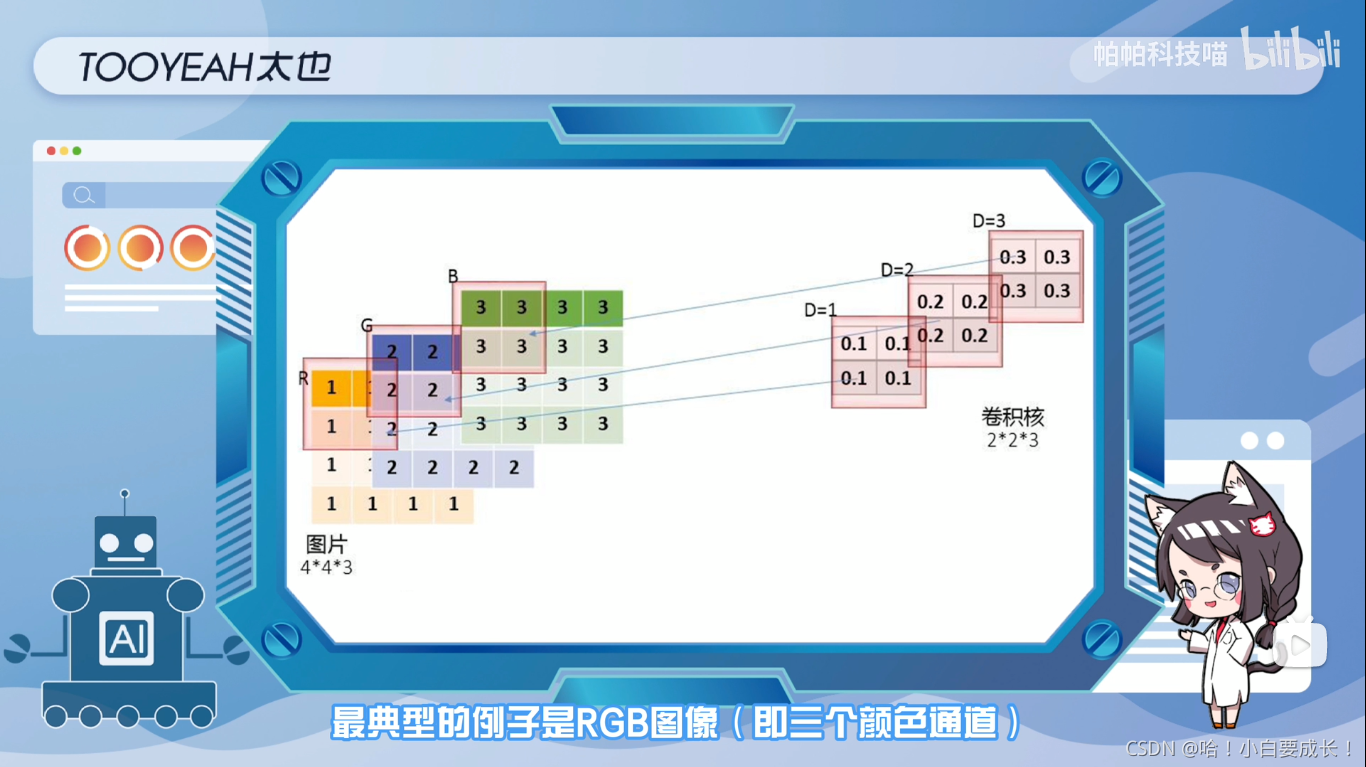
最典型的例子是RGB图像(即三个颜色通道),图中展示了多通道卷积的过程,输入层是一个5x5x3的矩阵,有三个通道滤波器是3x3x3矩阵。
首先,过滤器中的每个内核,分别应用于输入层中的三个通道,并相加。然后,执行三次卷积,产生三个尺寸为3x3的通道
产生步骤
第一步:将滤波器中的每个内核,分别应用于输入层中的三个通道
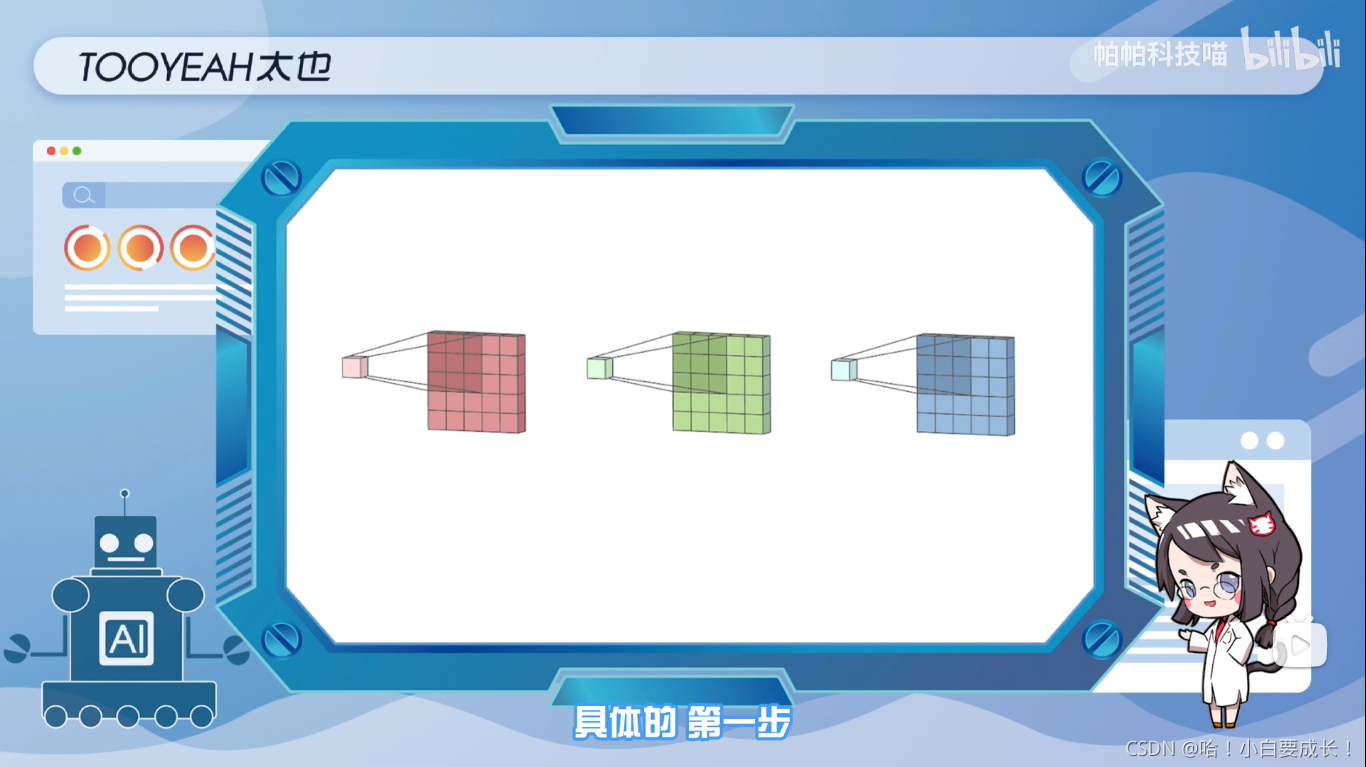
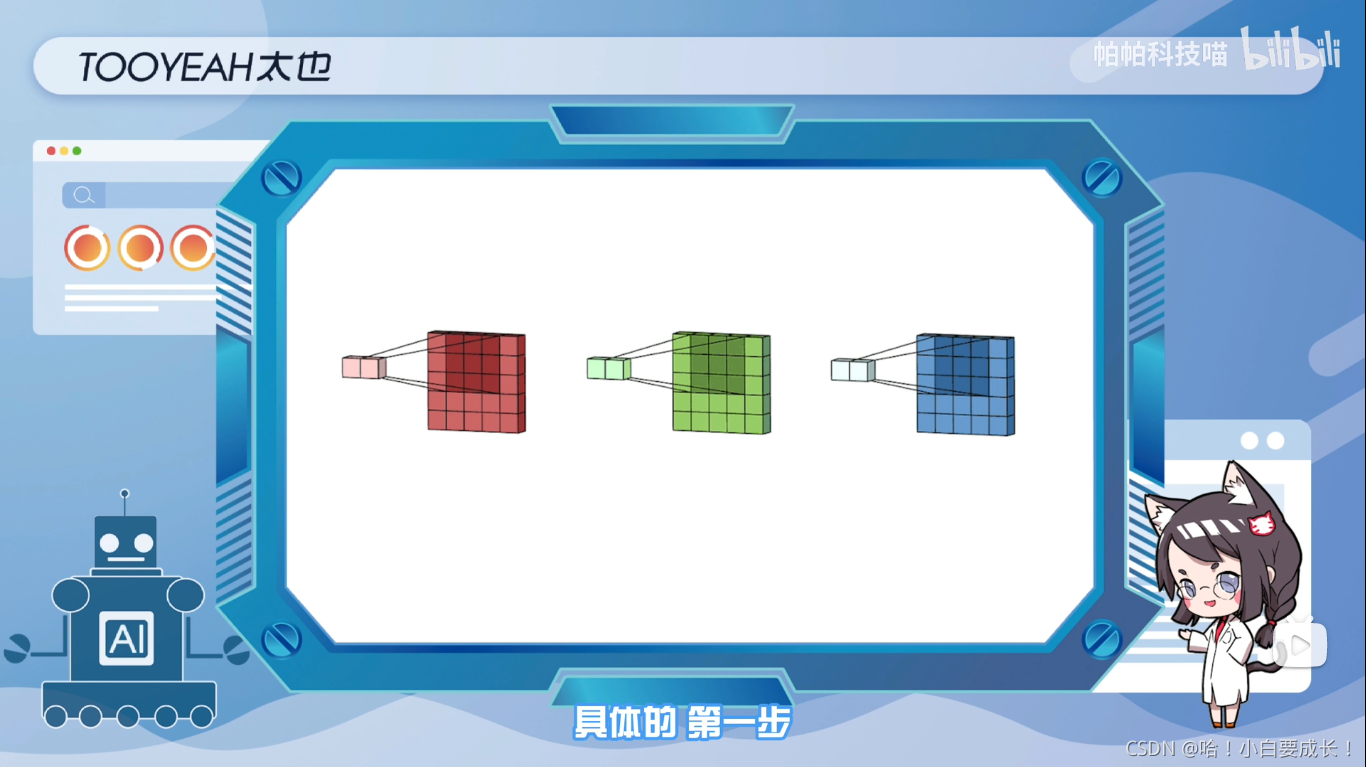
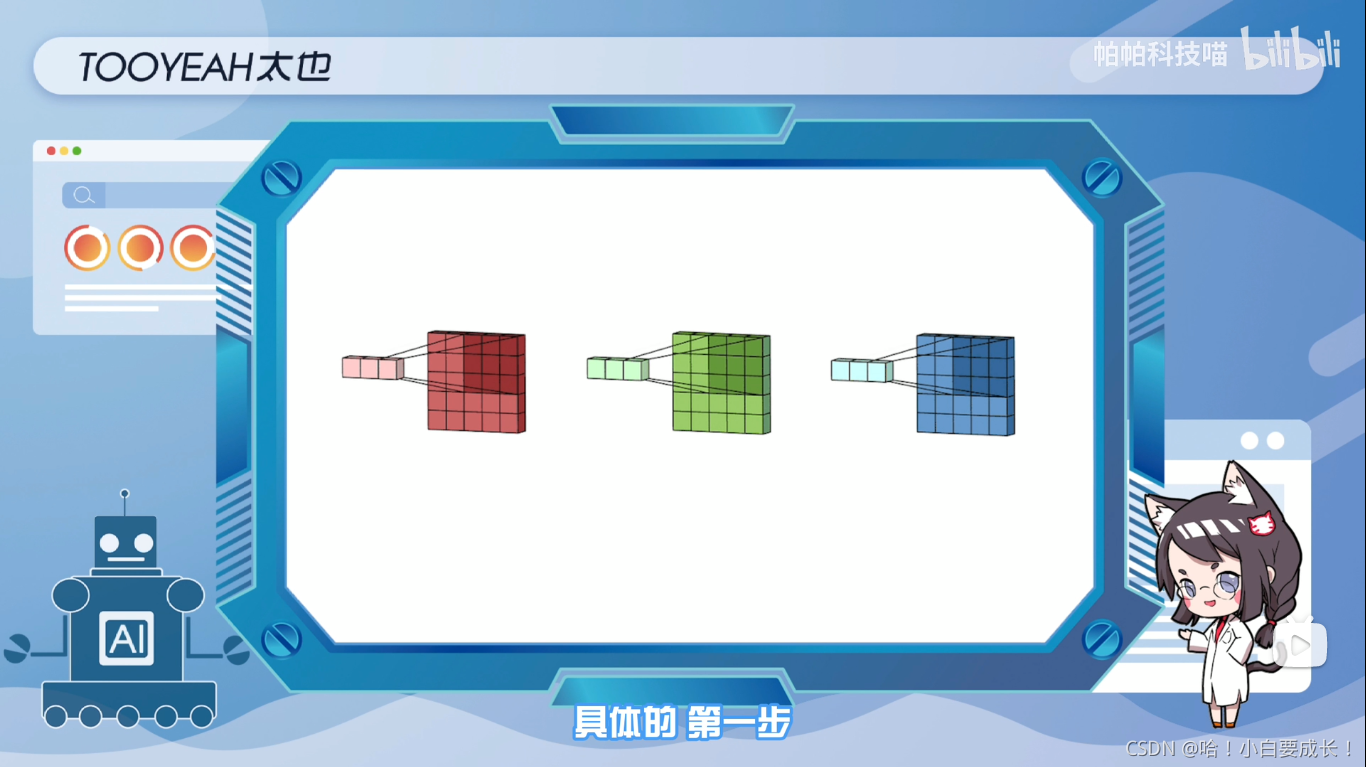
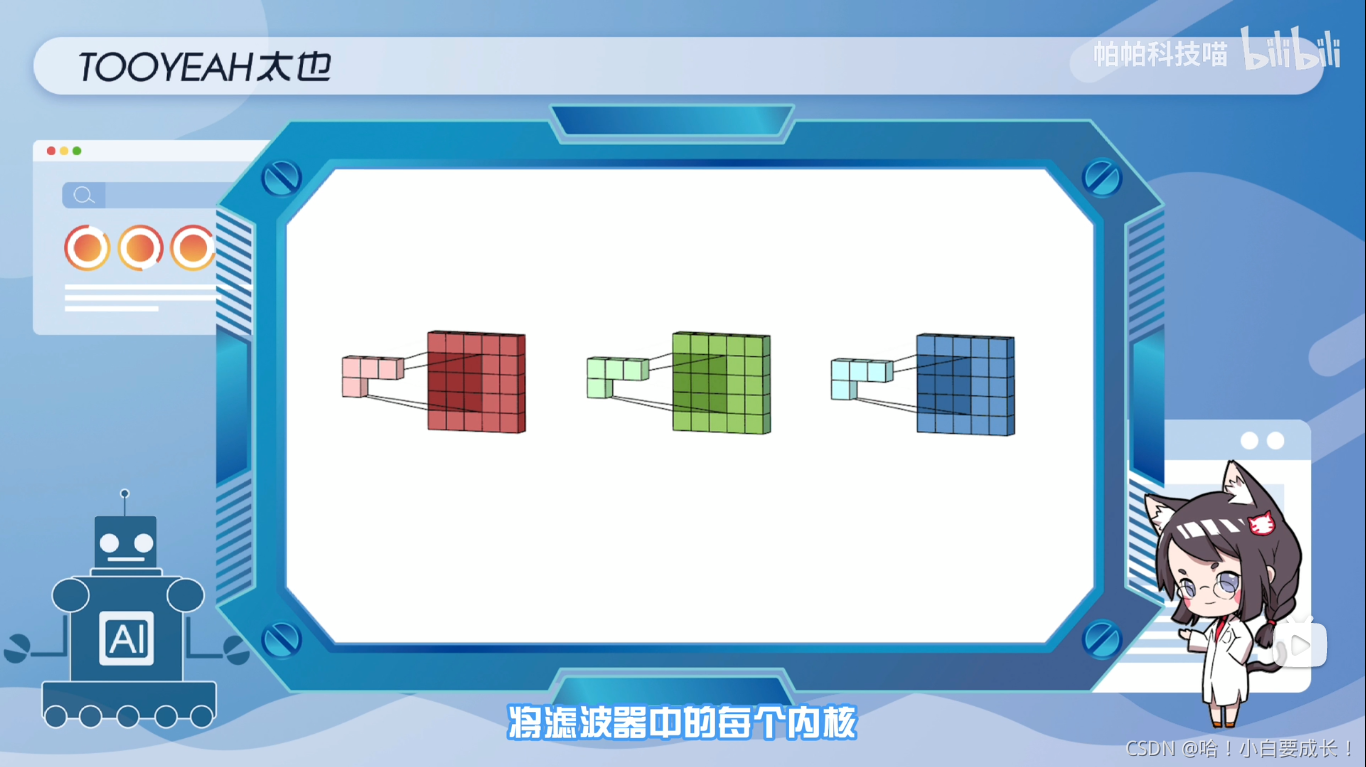
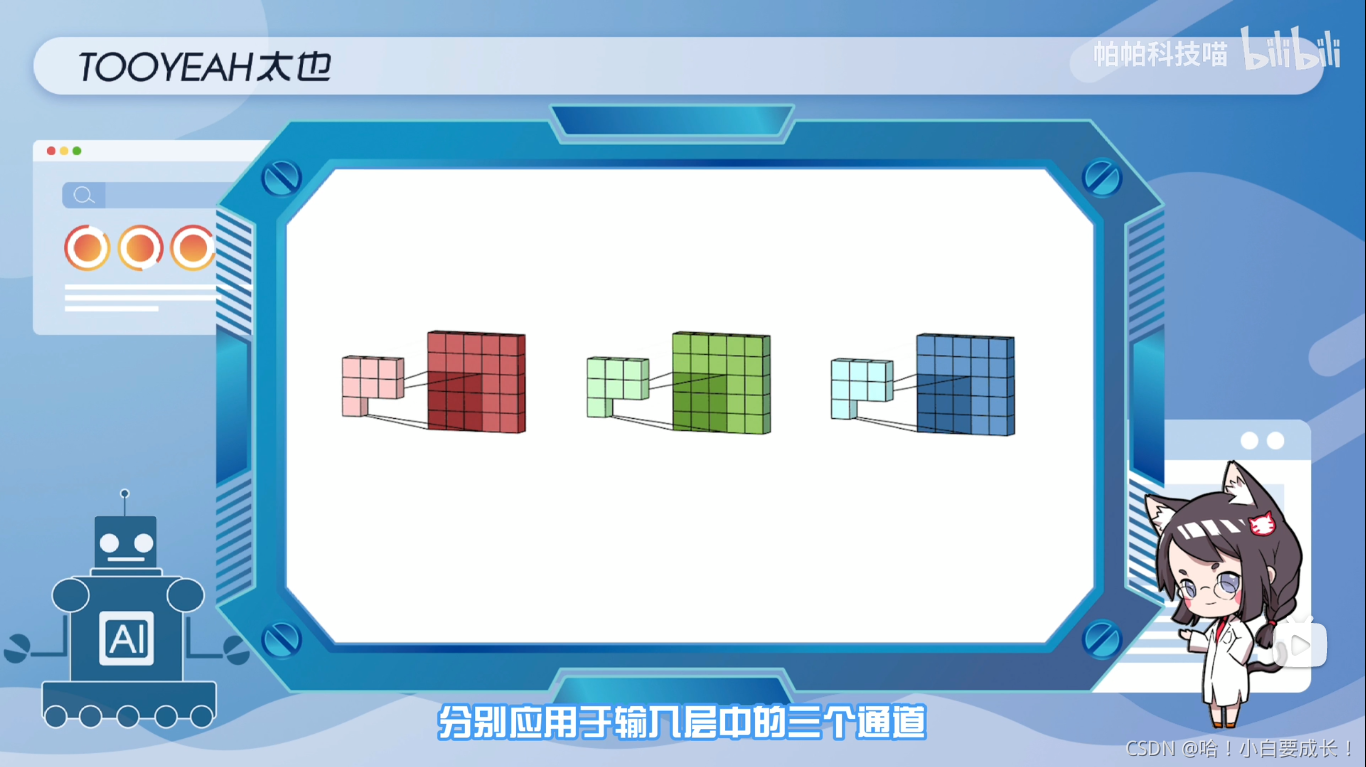
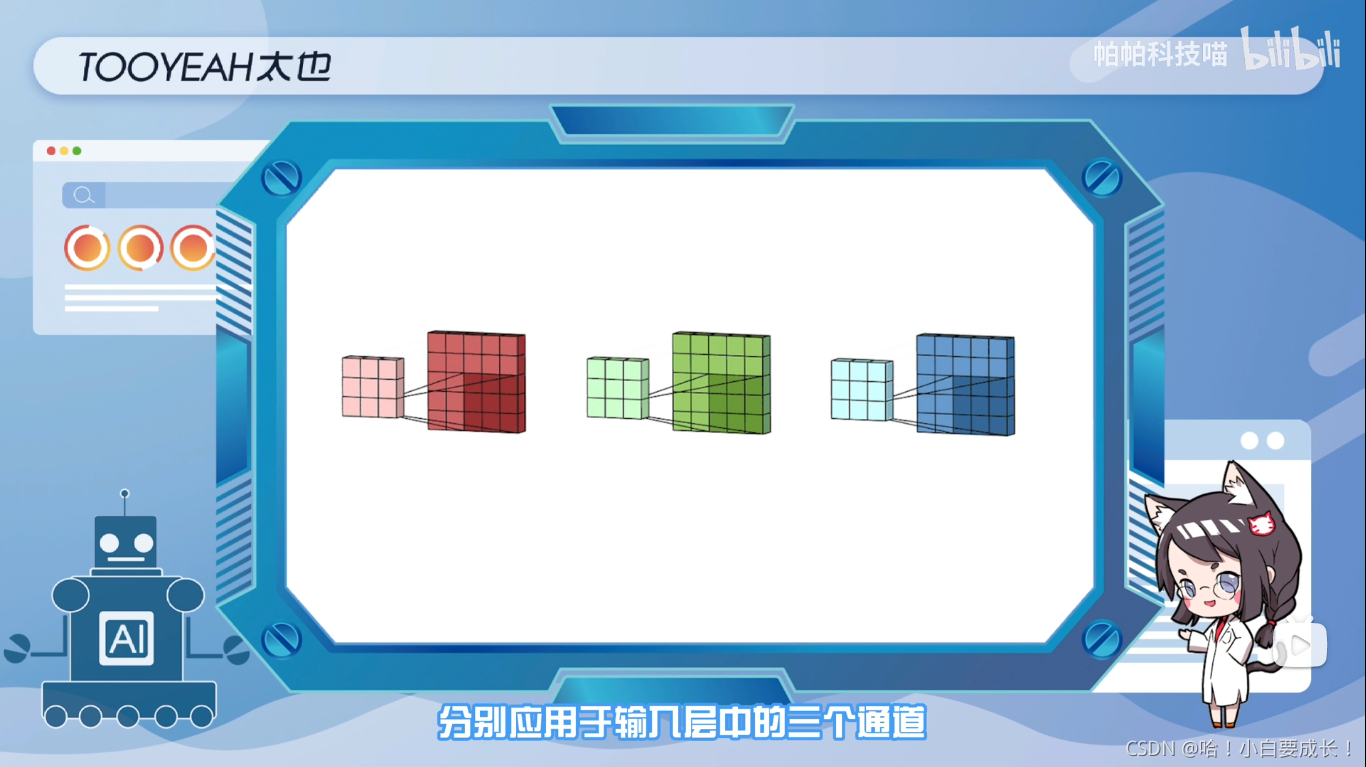
第二步:将滤波器中的每个内核,分别应用于输入层中的三个通道
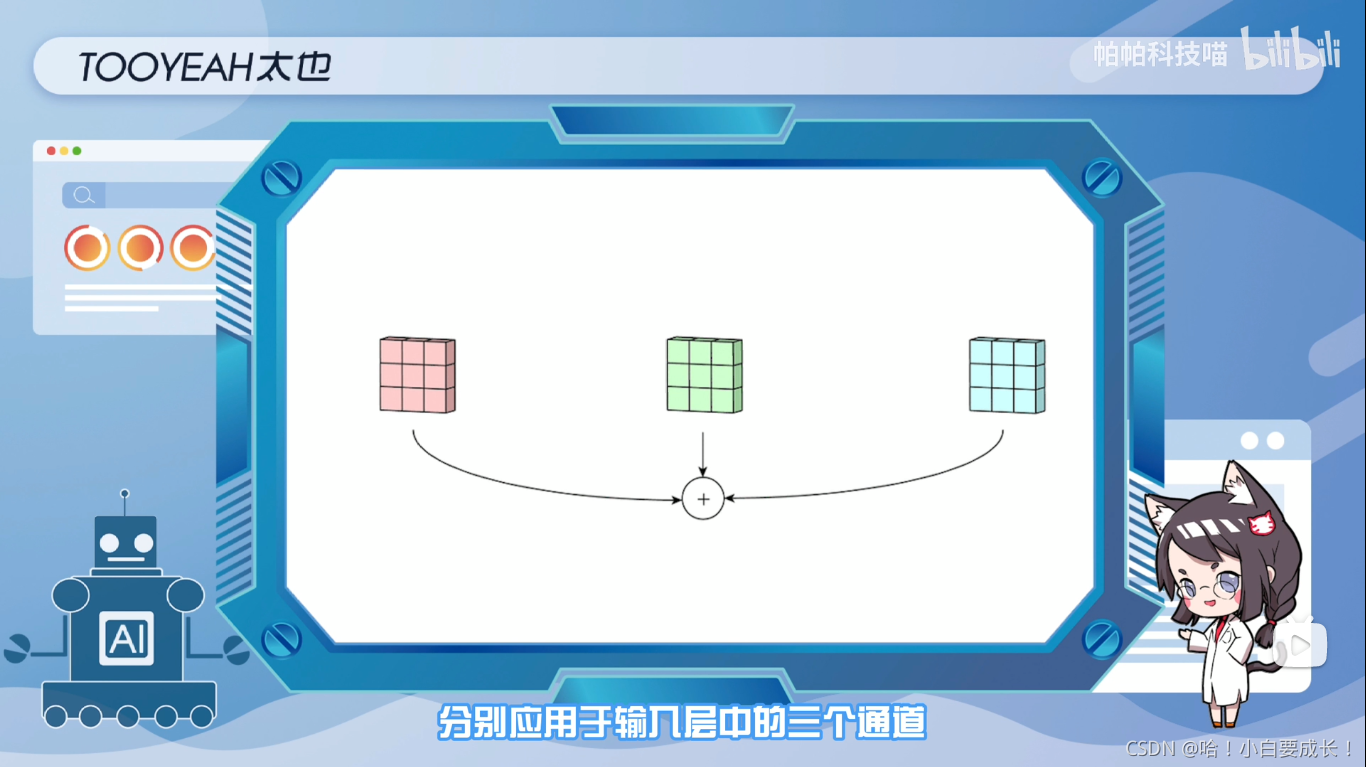
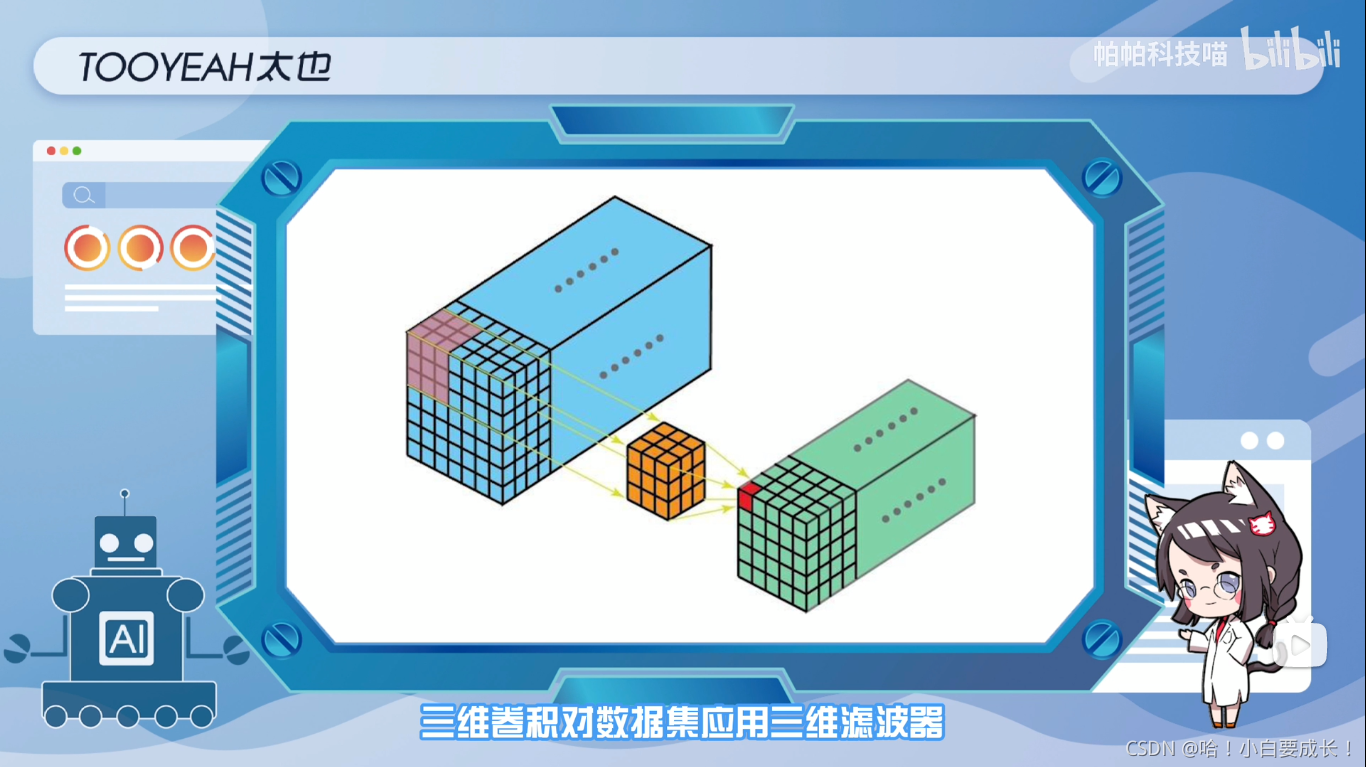
三维卷积
三维卷积对数据集应用三维滤波器,常用于视频、三维医学图像等事件检测中
其滤波器的深度小于输入层的深度(核大小<通道大小),因此,三维滤波器可以向3个方向(x,y,z)移动,计算特征表示,其输出形状也是一个三维的体积空间,如立方体或者长方体,
空间卷积
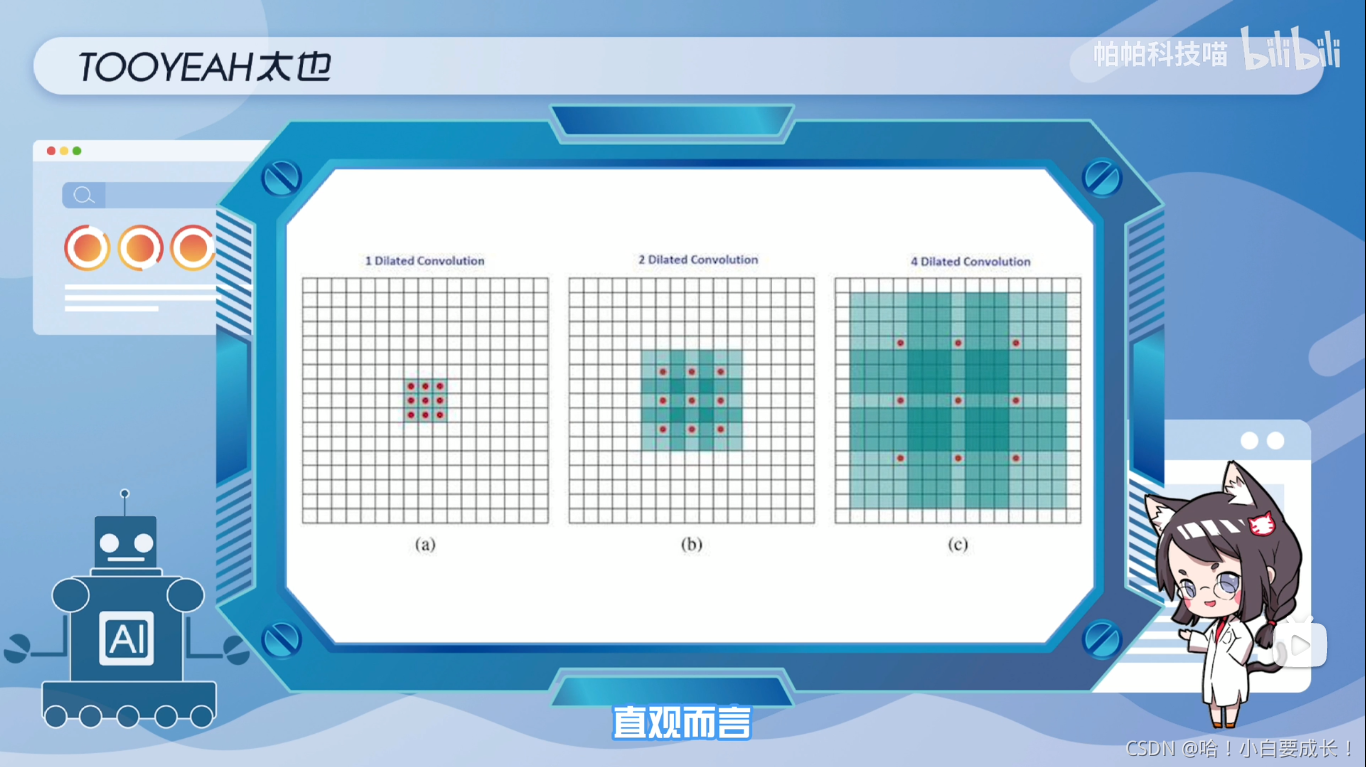
空间卷积广泛应用与语义分割和目标检测等任务中,它能在不需要引入额外参数的前提下,扩大感受野,捕获多尺度上下文信息。
直观而言,空洞卷积就是通过在核元素之间插入空格来使核“膨胀”,新增的参数L(扩张率)表示我们希望将核加宽的程度,通常是在核元素之间插入L-1个空格
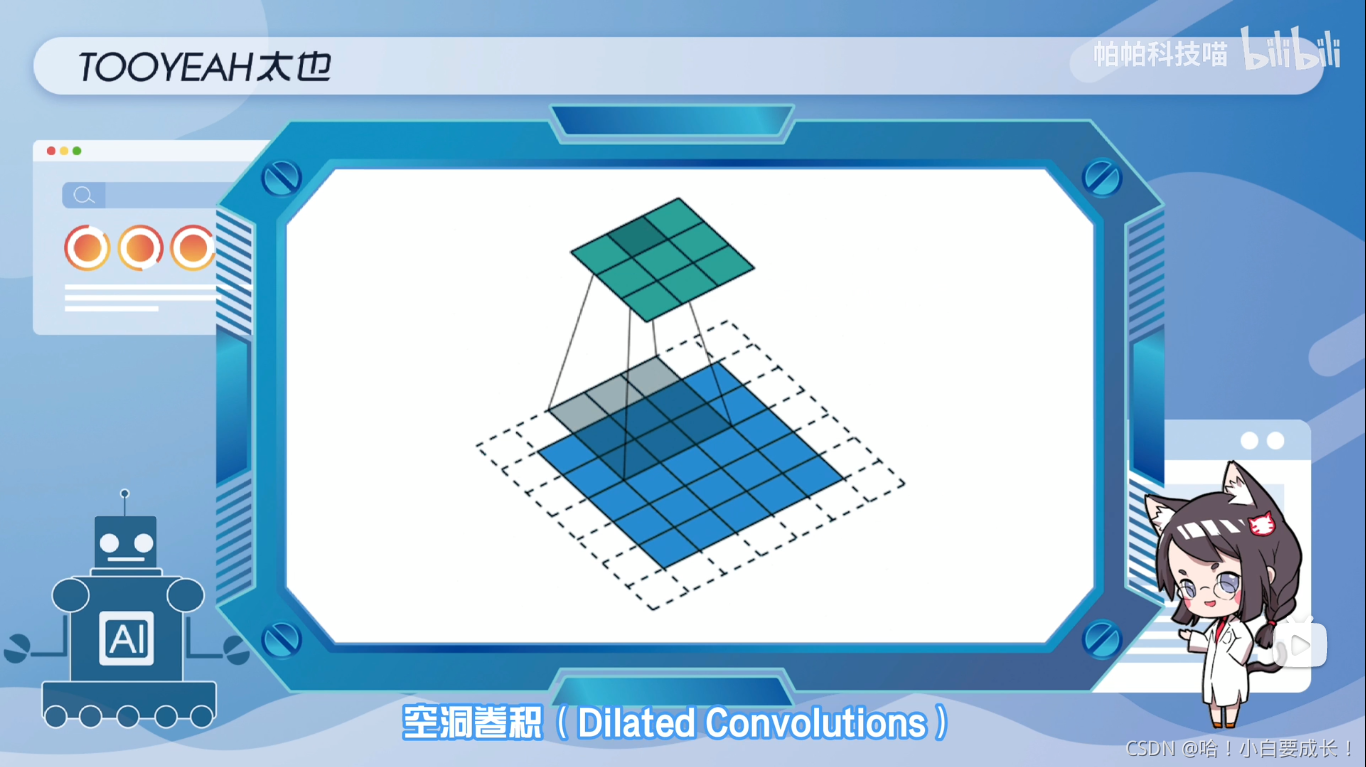
下面展示了L=1,2,4时的核大小
在语义分割任务中,如自动编码器的解码阶段,需要生成高分辨率图像,并将低维特征映射到高维空间,这时候我们希望进行与正常卷积相反方向的转换,即上采样
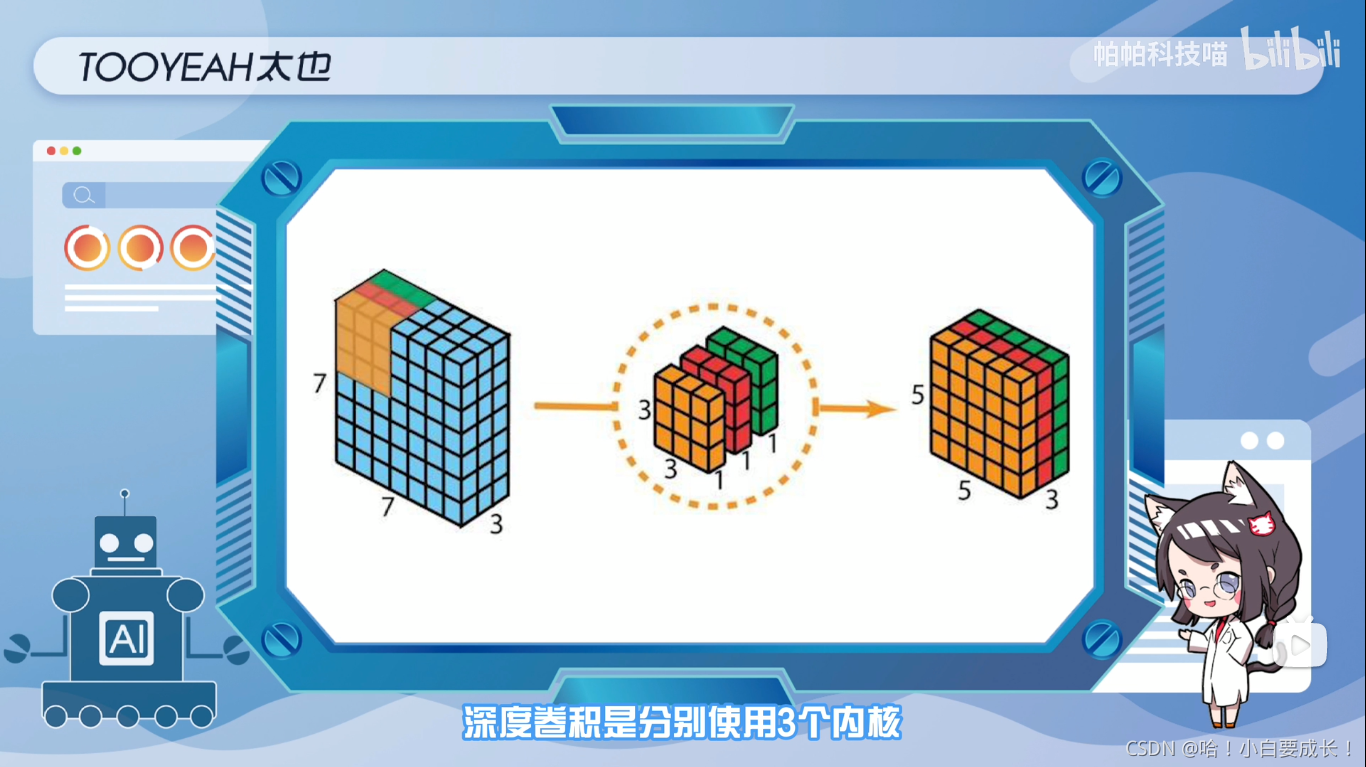
分别使用三个内核,每个内核大小是3x3x1,每个内核与输入层的一个通道进行卷积,每个这样的卷积,提供尺寸为5x5x1的图,然后将这些图堆叠在一起以创建5x5x3的特征矩阵,这样得到的输出矩阵的尺寸是5x5x3,缩小了空间尺寸,深度仍保持不变
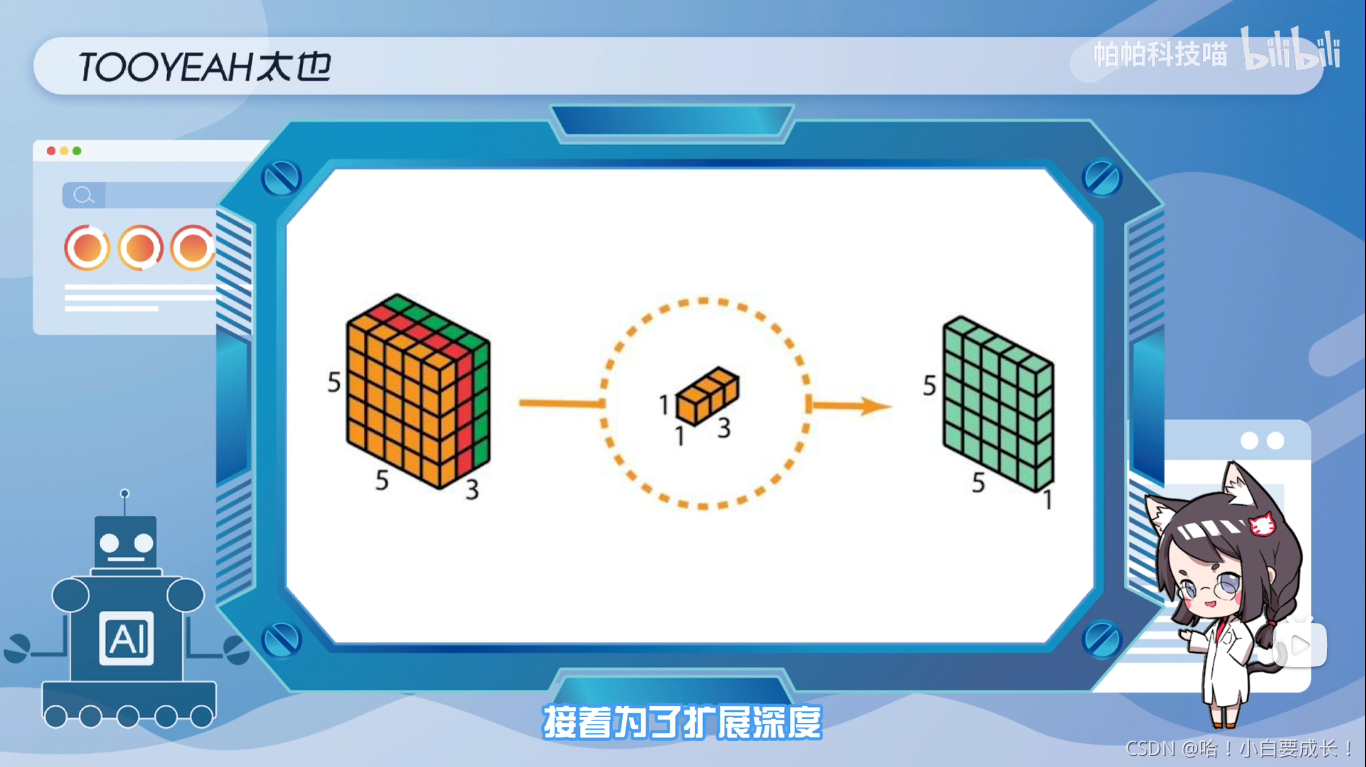
接着,为了扩展深度,应用1x1卷积,内核大小为1x1x3。将5x5x3输入图像与每个1x1x3内核进行对比,可提供大小为5x5x1的映射。在应用128个1x1卷积后,可得到一个尺寸为5x5x128的层
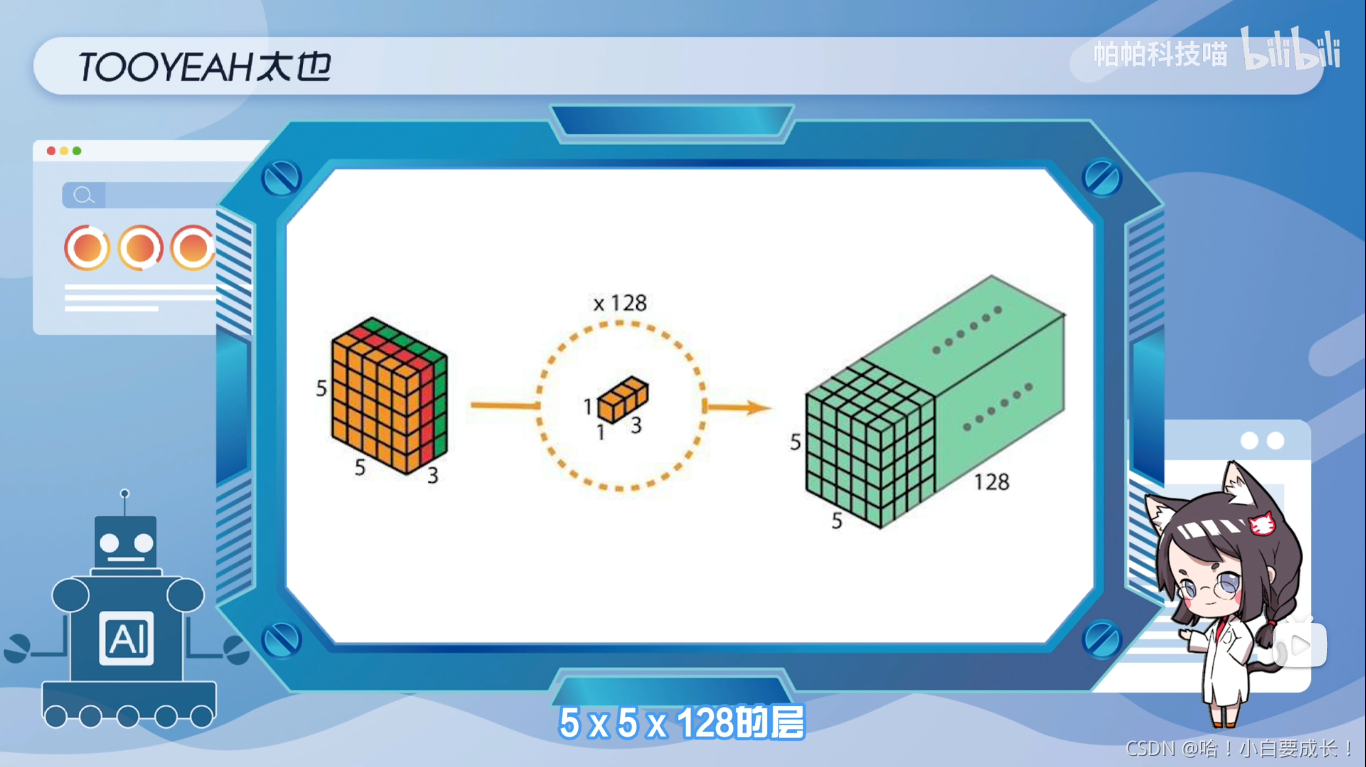
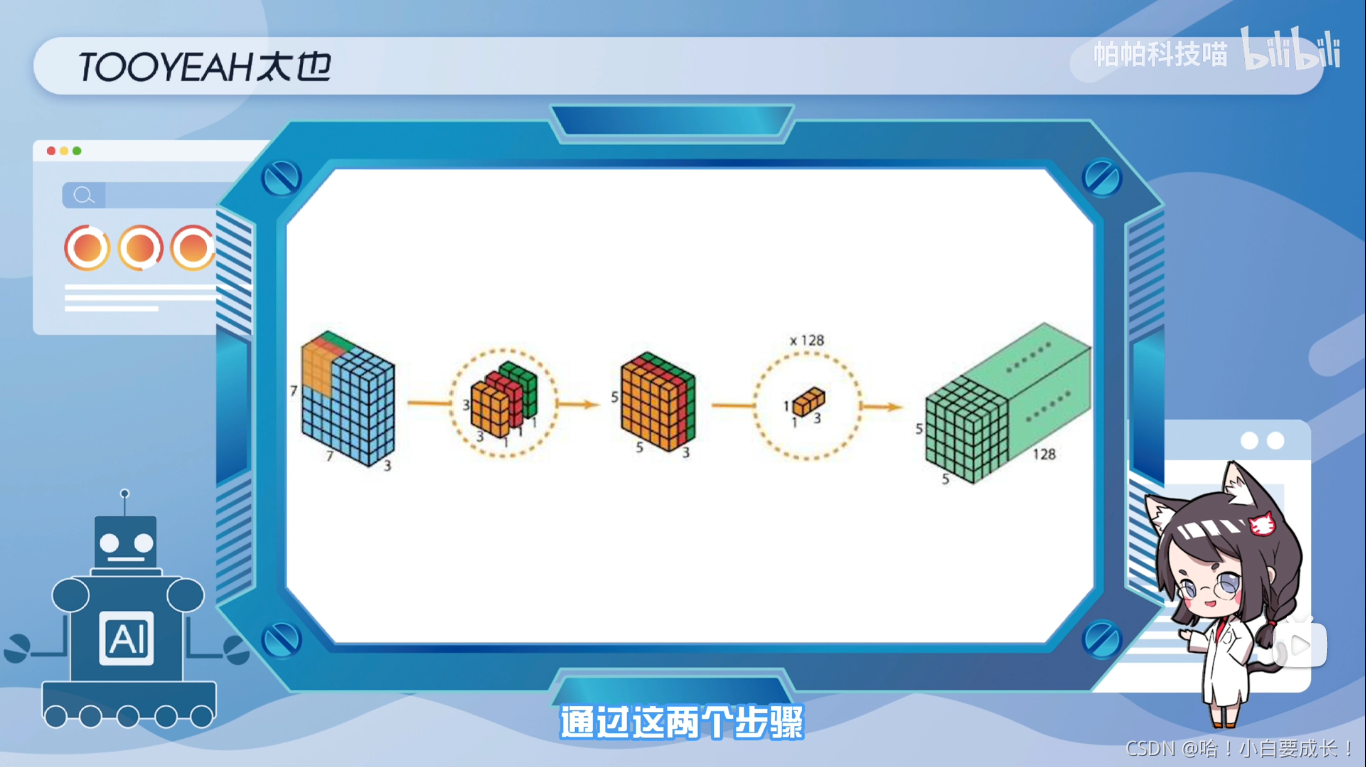
经过这两个步骤,深度可分离卷积便将输入层(7x7x3)转换为输出层(5x5x128)
线性时不变系统
英文:linear time invariant(LTI)
它包括连续时间系统与离散时间系统
线性时不变系统是根据系统输入和输出是否具有线性特性来定义的。满足叠加原理的系统具有线性特性。