Like What Y ou Like: Knowledge Distill via Neuron Selectivity Transfer------论文阅读笔记
写在前面
个人觉得这篇文章参考意义不大,过一遍就OK。
Abstract
在本文中,我们提出了一种新的知识转移方法,将其视为一个分布匹配问题。特别是,我们匹配了教师和学生网络中神经元选择性模式的分布。为了实现这一目标,我们通过最小化这些分布之间的最大平均差异(MMD)度量,设计了一个新的KT损失函数。结合原有的损失函数,我们的方法可以显著提高学生网络的性能。
1. Introduction
具体来说,我们利用神经元的选择性知识。这个模型背后的直觉相当简单:每个神经元基本上从原始输入中提取与手头任务相关的特定模式。因此,如果某个神经元在某些区域或样本中被激活,这意味着这些区域或样本共享一些可能与任务相关的共同属性。这种聚类知识对学生网络很有价值,因为它为教师模型的最终预测提供了解释。因此,我们建议在学生模型和教师模型之间调整神经元选择性模式的分布。。
KD 的知识是神经元的选择性知识的分布。
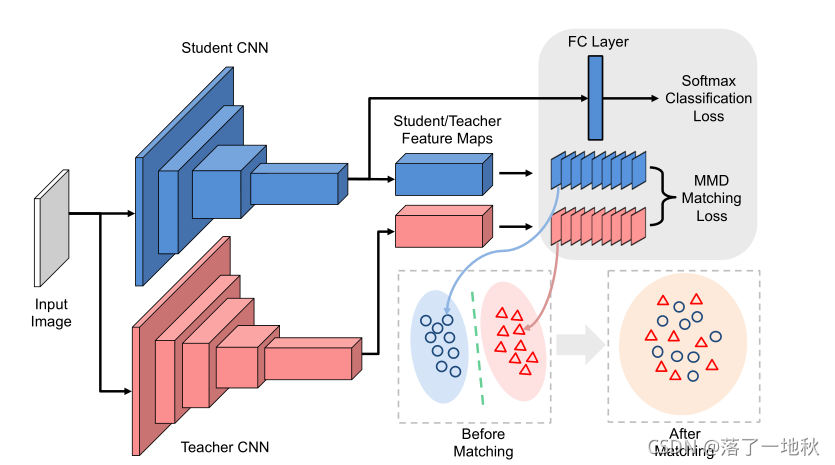
Figure 1. The architecture for our Neuron Selectivity Transfer: the student network is not only trained from ground-truth labels, but also
mimics the distribution of the activations from intermediate layers in the teacher network. Each dot or triangle in the figure denotes its
corresponding activation map of a filter.
图1. 我们的神经元选择性转移体系结构:学生网络不仅是根据地面真相标签进行训练,而且还模拟教师网络中间层的激活分布。图中的每个点或三角形表示其相应的过滤器激活图。
学生学习的是中间层的激活分布。这边文章的蒸馏也相对比较简单,一个是激活函数输出分布和传统输出蒸馏 ( 经过softmax 软化分布的输出)
2. Related Works
3. Background
3.1. Notations

假设要压缩的神经网络是卷积神经网络(CNN),教师网络称为T,学生网络称为S。
F : 表示 CNN 中某一层的输出特征映射 F∈ RC×HW ( C通道 和 空间尺寸 H×W )
fk·: 表示 F 的每一行(即每个通道的特征图)fk·∈ RHW
f·k: 表示F的每一列(即一个位置的所有激活)f·k∈ RC。
让 FT 和 FS 分别作为教师和学生网络特定层的特征图。
不丧失一般性的情况下,我们假设FT和FS具有相同的空间维度。如果尺寸不匹配,则可以对其进行插值。
3.2. Maximum Mean Discrepancy (最大平均偏差MMD)
MMD 是用来度量两个数据样本的 概率分布的距离
长见识了,概率分布的距离(差异)

两组样本 X 和 Y ,分布分别 p 和 q 那么,p 和 q 之间的平方MMD距离可以表示为上方公式。

φ(·)是一个显式映射函数。
进一步扩展它并应用内核技巧。
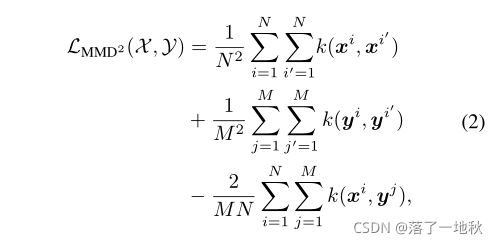
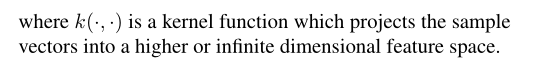
其中k(·,·)是一个核函数,它将样本向量投影到更高或无限维的特征空间。

再生核希尔伯特空间(RKHS)
可视化结果

4. Neuron Selectivity Transfer
4.1. Motivation
图2显示了与VGG16 Conv5 3中一个选定神经元的热图混合的两幅图像。
很容易看出这两个神经元具有很强的选择性:左图中的神经元对猴脸很敏感,而右图中的神经元对角色有强烈的激活作用。这种激活实际上意味着神经元的选择性,即什么样的输入可以激发神经元。换句话说,来自神经元的高激活区域可能具有一些与任务相关的相似性,即使这些相似性对于人类的解释可能不是直观的。为了捕捉这些相似性,在学生网络中也应该有神经元模拟这些激活模式。这些观察结果指导我们在教师网络中定义一种新的知识类型:神经元选择性或称为协同激活,然后将其转移到学生网络中。
What is wrong with directly matching the feature maps?
将每个空间位置的激活视为一个特征,将每个滤波器的平坦激活图 作为HW维 神经元选择性空间的样本 。这个样本分布反映了CNN如何解释输入图像:CNN关注的是什么?CNN更强调哪种类型的激活模式?对于分布匹配,直接匹配其中的样本不是一个好的选择,因为它忽略了空间中的样本密度。因此,我们采用了更先进的分布对齐方法,如下所述。
具体什么意思呢?
个人解释来说:1.HW 维度的平坦激活图 对于神经元空间位置选择 具有指导意义。2.未激活之前的特张图并不能清楚了解激活后 CNN 所关注的信息 和 激活方式 。
4.2. Formulation

fk·: 表示 F 的每一行(即每个通道的特征图)fk·∈ RHW ,代表特定神经元的选择性知识

H 就是传统对于输出的KD
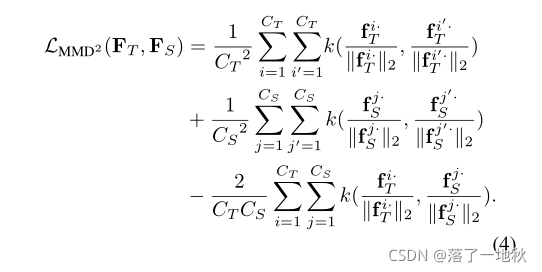

其中**k(·,·)**是一个核函数,它将样本向量投影到更高或无限维的特征空间。
MMD 最大平均偏差
k 的括号里是样本个例,只不过单位化了而已。
这里公式是因为二范式展开,没有什么难点。

这里核函数给了三个方法,线性,多项式,高斯。
4.3. Discussion
注意 : 归于本意 。 k 核函数是为了干嘛? 主要还是表示样本分布而演化而来的。
4.3.1 Linear Kernel

感觉这里作者故意混淆我们,公式换来换去的。
整理一下:
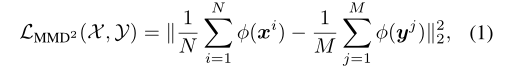
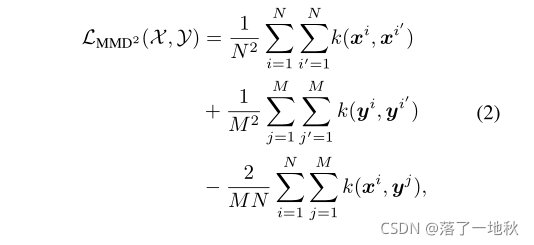
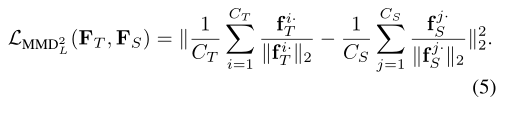
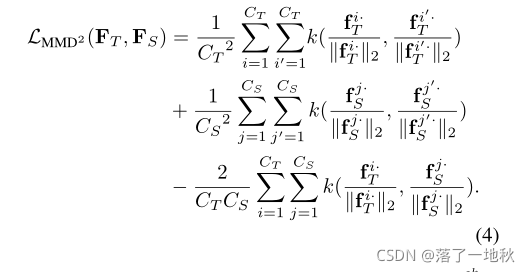
对于ReLU层之后的激活贴图,其已经是非负的,除归一化形式外,等式5等同于等式8。它们都代表了神经元有高反应的地方,即教师网络的“注意力”。因此,[38]在我们的框架中是一个特例。
归结于一点,Linear Kernel 的 核函数 k 激活函数后的,所想蒸馏的信息依旧还是注意力,因此该篇文章不具参考意义不大。
4.3.2 Polynomial Kernel
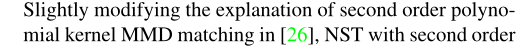

== 这里则表明多项式核函数 k ,当c = 0 是就转变成FSP 矩阵 ,相当于 FSP_KD 的想法。==
5. Experiments
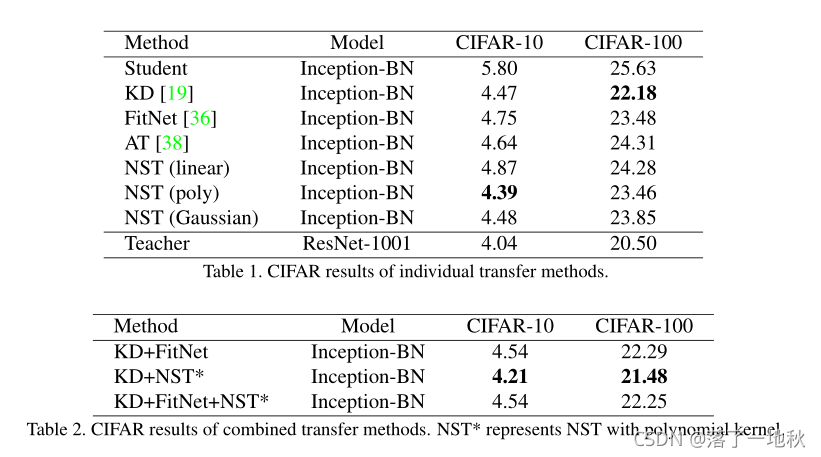
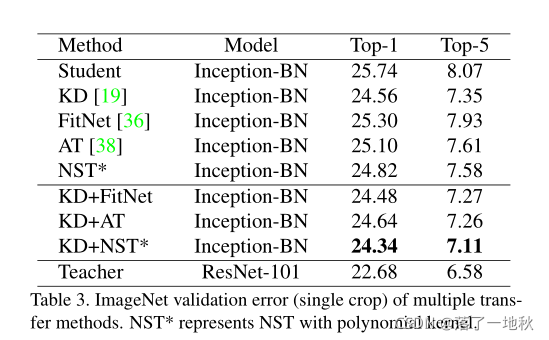

有什么错误欢迎指正!!!