回归分析Regression:
回归Regression:
回归一词最早由英国科学家弗朗西斯·高尔顿(Francis Galton)提出,他还是著名
的生物学家、进化论奠基人查尔斯·达尔文(Charles Darwin)的表弟。高尔顿深受
进化论思想的影响,并把该思想引入到人类研究,从遗传的角度解释个体差异形成
的原因。
? 高尔顿发现,虽然有一个趋势:父母高,儿女也高;父母矮,儿女也矮。但给定父
母的身高,儿女辈的平均身高却趋向于或者“回归”到全体人口的平均身高。换句
话说,即使父母双方都异常高或者异常矮,儿女的身高还是会趋向于人口总体的平
均身高。这也就是所谓的普遍回归规律。
? 高尔顿的这一结论被他的朋友,英国数学家、数理统计学的创立者卡尔·皮尔逊
(Karl Pearson)所证实。皮尔逊收集了一些家庭的1000多名成员的身高记录,发
现对于一个父亲高的群体,儿辈的平均身高低于他们父辈的身高;而对于一个父亲
矮的群体,儿辈的平均身高则高于其父辈的身高。这样就把高的和矮的儿辈一同
“回归”到所有男子的平均身高,用高尔顿的话说,这是“回归到中等。
一元线性回归
回归分析通过建立方程模拟两个或多个变量之间如何关联。
一元线性回归主要是方程,包含了自变量(dependent variable)与因变量(independent variable)
如果包含两个及以上的自变量,我们称为多元回归分析
(multiple regression)
?𝜃 𝑥 = 𝜃0 + 𝜃1𝑥
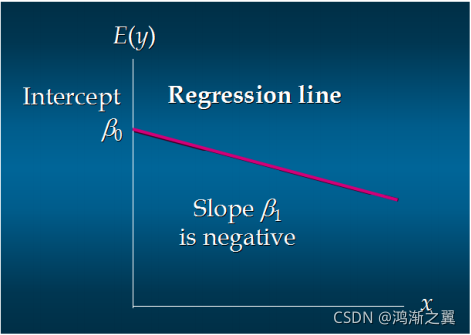
这个方程对应的图像是一条直线,称作回归线。其中,
𝜃1为回归线的斜率, 𝜃0为回归线的截距
一元线性回归-正相关

一元线性回归-负相关
一元线性回归-不相关

代价函数Cost Function:
最小二乘法
真实值y,预测值?𝜃 𝑥 ,则误差平方为 y ? ?𝜃 𝑥 2
找到合适的参数,使得误差平方和:
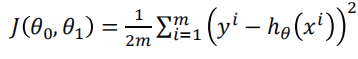
最小

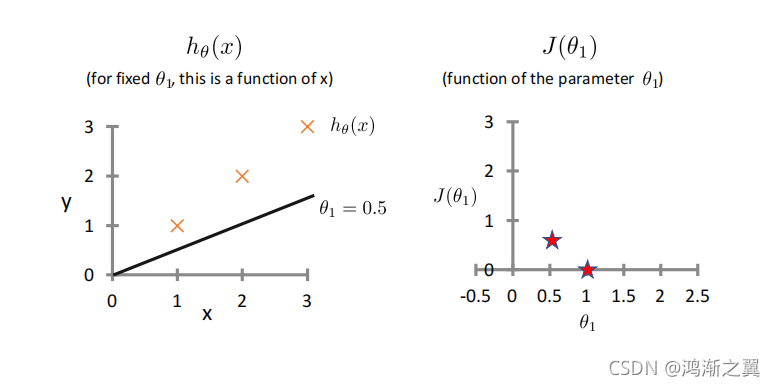
假设Hypothesis:
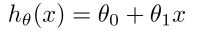
简化 Simplified:
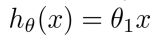
参数Parameters:

代价函数Cost Function:
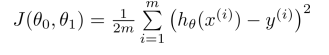
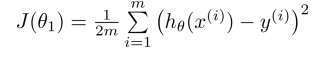
目标Goal:
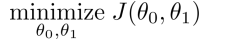
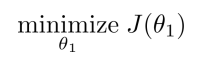







相关系数
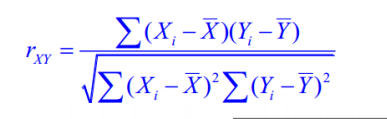
相关系数𝑅2
(coefficient of determination)是用来
描述两个变量之间的线性关系的,但决定系数的适
用范围更广,可以用于描述非线性或者有两个及两
个以上自变量的相关关系。它可以用来评价模型的
效果。
总平方和(SST):
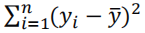
回归平方和(SSR):
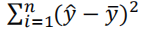
残差平方和(SSE):
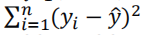
三者关系:
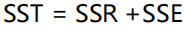
决定系数:
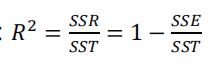
————————————————
本文参考 机器学习 覃秉丰