
本文是基于《机器学习实战》配套的tools_numpy 的notebook文件写的
具体可查看
https://homl.info/kaggle/
创建数组
首先导入numpy
import numpy as np
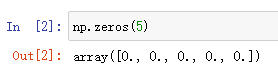
np.zeros
zeros函数用于创建包含任意个数0的数组
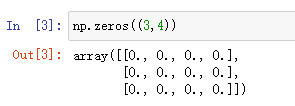
创建二维数组:
注意区别:
一维数组:np.zeros(数字) 输出:array( [数字,数字,…] )
二维数组:np.zeros( 元组 ) 元组=(数字,数字…) 输出:array( [ [ 数字,数字,…], ] )
二维数组和三维数组的对比:

一些术语
- 在numpy,每一个维度称为axis
- axis的数量称为rank
如,上面3x4的矩阵是一个rank为2的数组,因为它是二维的
第一个axis长度为3,第二个axis长度为4 - 数组的shape
- 数组的size就是所有axis长度的内积,也就是数组中元素的个数 (如:3 x 4 =12)

array.shape输出的是一个元组 (第一个axis的长度,第二个axis的长度,…)
array.ndim输出的是维度的个数 就是有多少个axis
array.size输出的是数组里面究竟有多少个元素
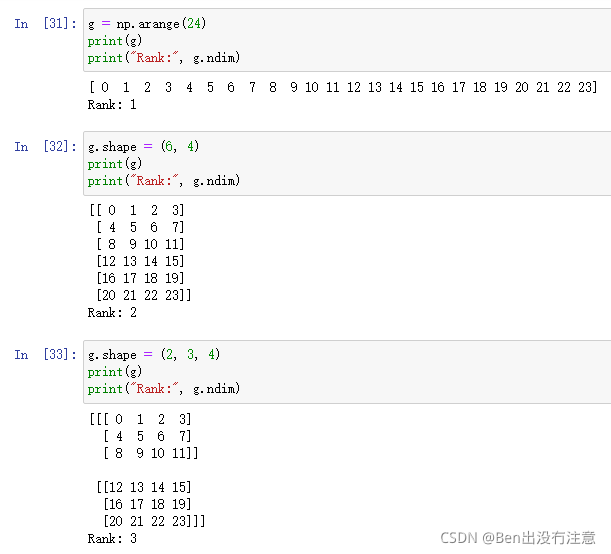
N维数组

数组类型
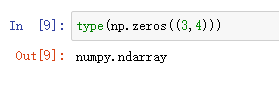
numpy的数组类型是ndarray
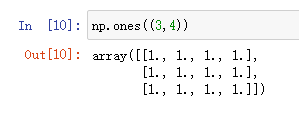
np.ones
用于创建元素全是1的ndarrays
np.full
给定一个值(given value),创建一个填满给定值的矩阵
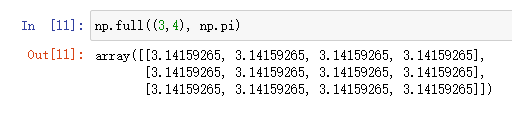
调用格式:np.full(给定数组大小,给定值)
np.empty
生成未初始化的数组,其中内容不可预测,根据当时内存中的值

np.array
通过常规的python array来初始化ndarray

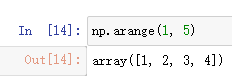
np.arange
类似于Python的内置range 函数,调用后会创建一个ndarray
不带步进参数的(默认步进长度为1)
整数:
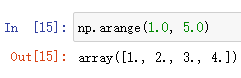
浮点数:
带步进参数的

形式:np.arange(头,尾,步进值)
然而,当面对浮点数的时候,在数组中元素的个数并不总是可以预测的,如:
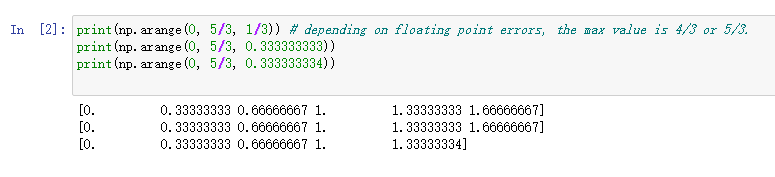
基于这个原因,我们一般更常用np.linspace函数来生成等间隔的数组。
np.linspace

区别:linspace函数返回一个包含具体个数的等间距的数组(包括尾值,这是与arange函数不同的地方)
形式:np.linspace(头,尾,数组中要分隔元素的个数)
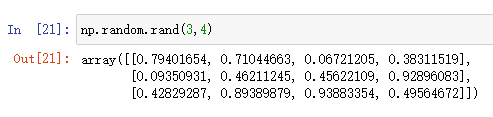
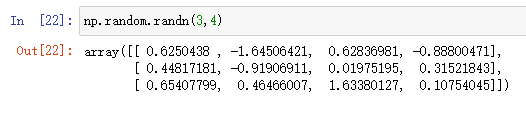
np.rand 和 np.randn
区别:
np.random.rand是在取值为0到1之间的均匀分布
np.random.randn是均值为0,方差为1的高斯分布
np.fromfunction
你也可以通过使用一个函数来初始化ndarray
例子:

NumPy首先创建三个数组(每个维度一个),每个数组都是形状(3,2,10)。每个数组的值等于沿特定轴的坐标。例如,z数组中的所有元素都等于它们的z坐标:

所以上面的表达式x + 10 * y + 100 * z中的项x,y和z实际上是数组(我们将在下面讨论数组的算术运算)。关键是函数my_function只被调用一次,而不是每个元素调用一次。这使得初始化非常高效。
数组数据
dtype
numpy的ndarray通常很高效是因为他们的所有元素必须具有相同的类型。可以用dtype属性来查看数据的类型

你设置可以显式地设置使用哪种数据类型,如dtype=np.conlex64

常见的数据类型包括:int8, int16, int32, int64, uint8|16|32|64, float16|32|64 and complex64|128
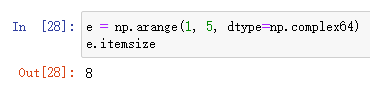
itemsize
itemsize属性返回的是各item所占据的字节数
data buffer
一个数组数据实际上是被压扁为一维度存在。你可以通过data 属性才查看,虽然很少用得上
几个ndarrays可以共享相同的数据缓冲区,意味着修改一个也会修改其它ndarrays
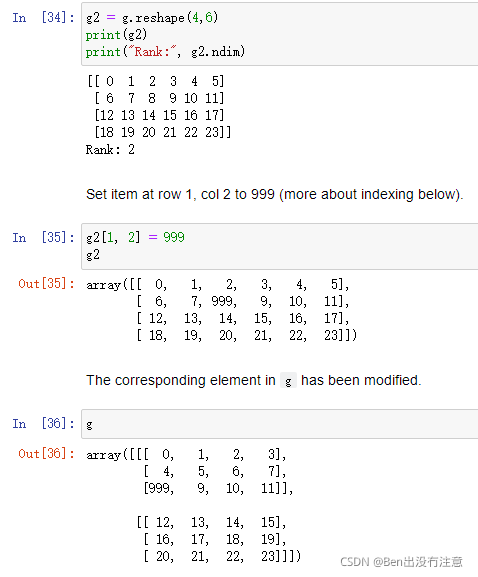
重塑一个数组
In place
reshape
注意:reshape函数返回一个新的ndarray对象但指向相同的数据。这意味着修改一个数组同时会修改另外一个
例子:
ravel
ravel函数主要是提供扁平化操作(就压缩到一维),类似地有flatten函数,但彼此之间又存在着差异
ravel函数返回一个新的一维ndarray,但依然指向相同的数据

算术操作
所有的常见算术操作(加、减、乘、除、求余、次方)都可以用在ndarray,他们基于单元素层面应用。

注意:可以看到是相应位置元素与元素之间的运算,乘法并不是矩阵乘法。
数组必须具有相同的形状,否则,numpy会自动应用广播
广播
First rule
If the arrays do not have the same rank, then a 1 will be prepended to the smaller ranking arrays until their ranks match.
如果数组之间不具有相同的形状,则一个1会被添加在较小的rank,直到它们的rank匹配

比如一维数组的shape是(5,),如果要加到这个三维数组(1,1,5),就自动扩充为(1,1,5)
Second rule
Arrays with a 1 along a particular dimension act as if they had the size of the array with the largest shape along that dimension. The value of the array element is repeated along that dimension.(说实话,不会翻译,大概就是沿着axis=1的那个方向进行扩展)
例子:

这是一个2 x 3矩阵
加上一个2 x 1的数组,即axis0=2 , axis1 =1 广播沿着axis1的方向进行

假如加上一个1 x3 的数组,即axis0=1 广播沿着axis0的方向进行

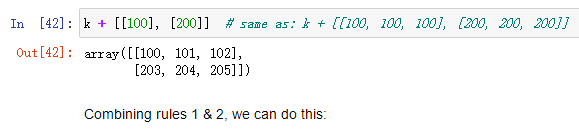
Third rule
After rules 1 & 2, the sizes of all arrays must match.
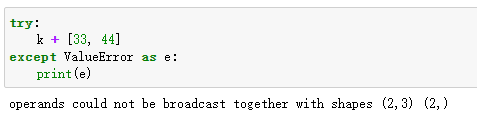
怎么去思考这个例子呢?
首先,根据Rule 1 ,[33,44]是一维数组,shape是(2,),扩展为(1,2)
根据Rule2,从axis0=1这个维度进行扩展为(2,2),此时无法与shape(2,3)匹配
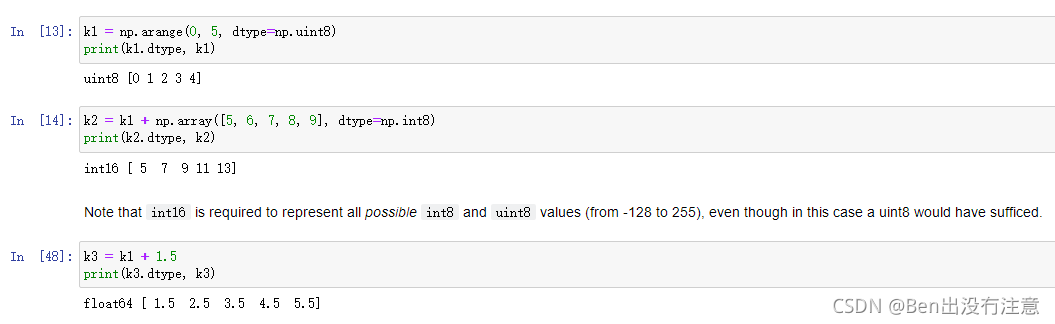
向上类型转换(Upcasting)
当试图组合具有不同数据类型的数组时,Numpy将向上转换为能够处理所有可能值的类型,如int 和float合并时,就自动将int类型的数据转换为float
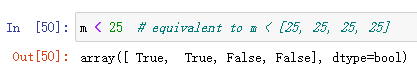
条件运算符(Conditional operators)
条件运算符基于元素操作。

还可以利用广播( broadcasting)
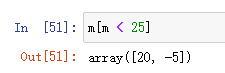
与boolean indexing相结合是最有用的
数学与统计函数Mathematical and statistical functions
ndarray 的方法
ndarray.mean()
作用:取所有元素的均值
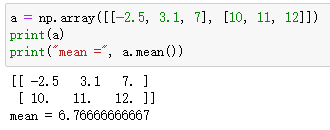
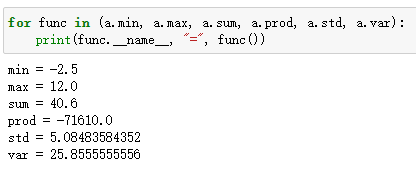
ndarray.min() ndarray.max() ndarray.sum() ndarray.prod() ndarray.std() ndarray.var()
作用:最小值 最大值 总和 元素的乘积 标准差 方差
甚至还可以指定axis相加的方向

甚至还可以在多个axis方向上同时求sum
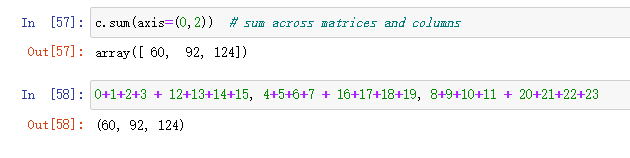
总结
指定哪个axis就往哪个axis上压缩,比如指定axis(0,2),先消灭axis0,就是把两个3x4矩阵叠在一起,再消灭axis2,从左到右,把列叠加。
通用功能(Universal functions)
NumPy还提供了称为通用函数(ufunc)的快速elementwise函数。它们是简单函数的矢量化包装。例如,square返回一个新的数组,它是原始数组的副本,只是其中的每个元素是被平方过的。
square()
作用:对数组中的每个元素单独平方

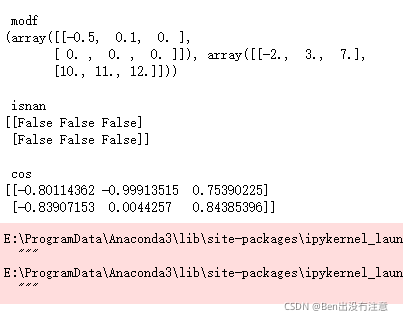
abs()、sqrt()、exp()、log()、sign()、ceil()、modf()、isnan()、cos()
作用:绝对值、开方、指数、对数、符号函数、向上取整、返回整数和小数部分、判断一个数是否NaN、余弦函数
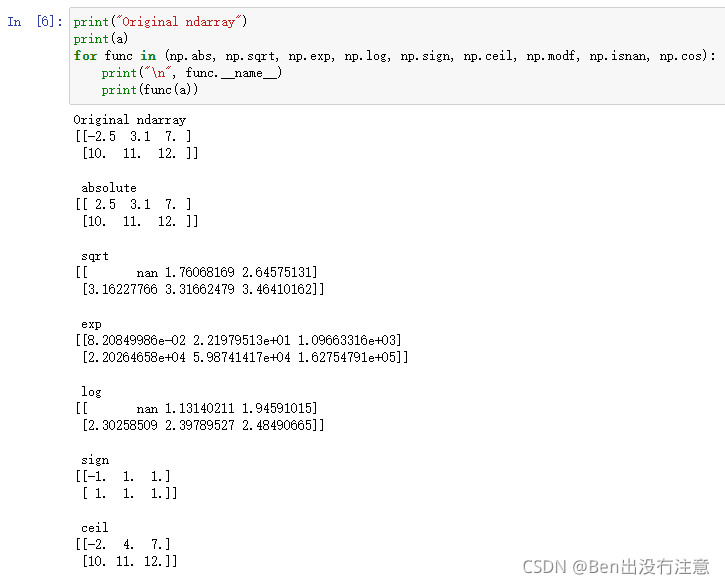
细节:关于sign函数 https://blog.csdn.net/weixin_42708378/article/details/95485491
关于ceil函数 https://blog.csdn.net/qq_40178291/article/details/100769910
modf函数就是把整数部分和小数部分分成两个array单独分开返回
isnan函数 https://www.jianshu.com/p/77abe8b7ea8e
Binary ufuncs()
就是输入需要两个数组,如果输入的两个数组的形状不一致,就会使用广播(Broadcasting)
np.add()
作用:把两个数组相加

np.greater(a,b)
作用:判断a数组中的元素对应b数组中的元素是否大于,并返回一个bool类型的数组

np.maximum(a,b)
作用:a和b数组中对应元素一一比较,选择最大值返回。
如:
a = np.array([1, -2, 3, 4])
b = np.array([2, 8, -1, 7])
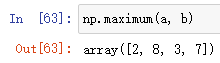
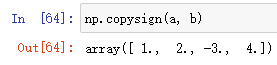
np.copysign(a,b)
作用:把b数组中的符号赋值给a数组,并返回浮点值数组
Array indexing(数组索引)
One-dimensional arrays (一维数组)
一维numpy array跟普通python 数组差不多

复杂一点:
a[start : stop : step]


这里-1就是倒序输出

Differences with regular python arrays
与常规的Python数组相反,由于前面讨论到广播机制,如果你为ndarray切片分配一个值,它会改变整个slice。

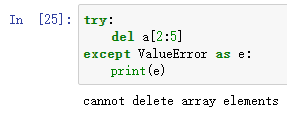
同时,你不能像这样子增长或者缩小ndarray:

你也不能像这样删除元素:
最后但同样重要的是,数组切片实际上是同一数据缓冲区上的视图,这意味着,如果您创建一个切片并对其进行修改,你实际上也修改了原始的ndarray。
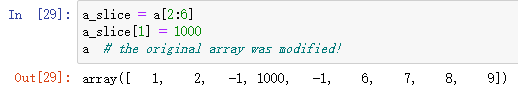
同样地,修改切片的同时也会修改原来的ndarray。

如果你想要一份数据的copy,你需要使用copy方法:
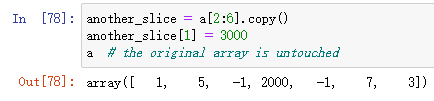
这样修改切片的时候原数据就不会被改动。

多维度数组
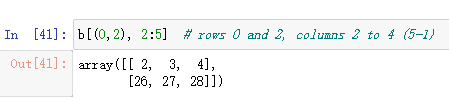
通过为每个轴提供一个索引或切片(用逗号分隔),可以以类似的方式访问多维数组。

注意以下两个表达式之间的细微区别。

第一个表达式将第1行作为形状(12,)的1D数组返回,而第二个表达式将该行作为形状(1,12)的2D数组返回。
Fancy indexing(花式索引)

如果提供多个索引数组,则会得到一个一维数组,其中包含指定坐标处元素的值。

Higher dimensions(更高维度)

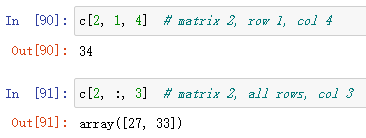
如果省略某些axis的坐标,则返回这些轴中的所有元素:

省略号 Ellipsis (…)
你也可以写一个省略号把所有未指定的axis包含在内。

布尔索引

np.ix_
作用:np.ix_函数,能把两个一维数组 转换为 一个用于选取方形区域的索引器

np.ix_函数,将[0,2]和数组[1,4,7,10]产生笛卡尔积,就是得到(0,1),(0,4),(0,7),(0,10),(2,1),(2,4),(2,7),(2,10)
详细例子:https://blog.csdn.net/weixin_40001181/article/details/79775792
如果使用与ndarray具有相同形状的布尔数组,则返回一个1D数组,其中包含在其坐标处为True的所有值。这通常与条件运算符一起使用:

迭代(Iterating)
在Ndarray上迭代与在常规python数组上迭代非常相似。请注意,对多维数组的迭代是相对于第一个axis完成的。
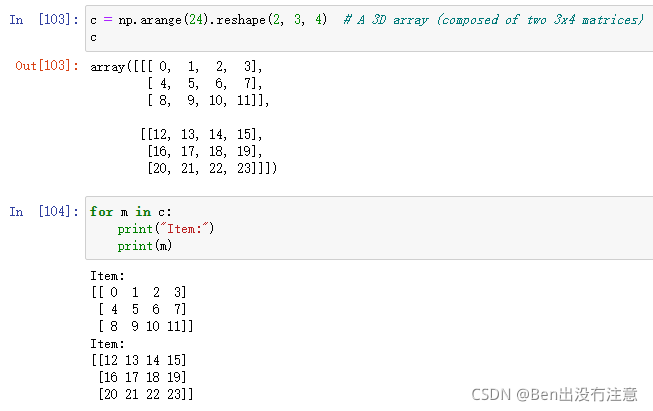
ndarray的len就是axis0的取值。

如果你想要遍历ndarray中的所有元素,直接循环 flat 属性

Stacking arrays(堆叠数组)

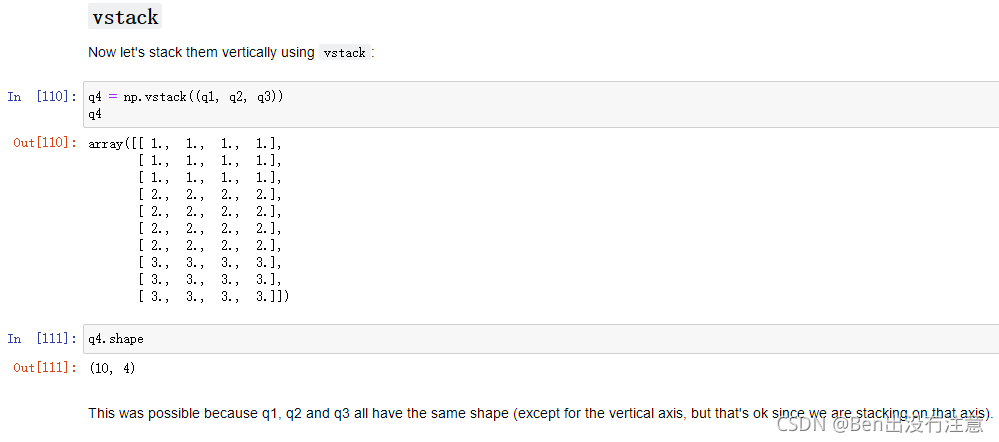
np.vstack
作用:垂直叠加(vertical),相当于往行的方向上增加,前提是列数相同
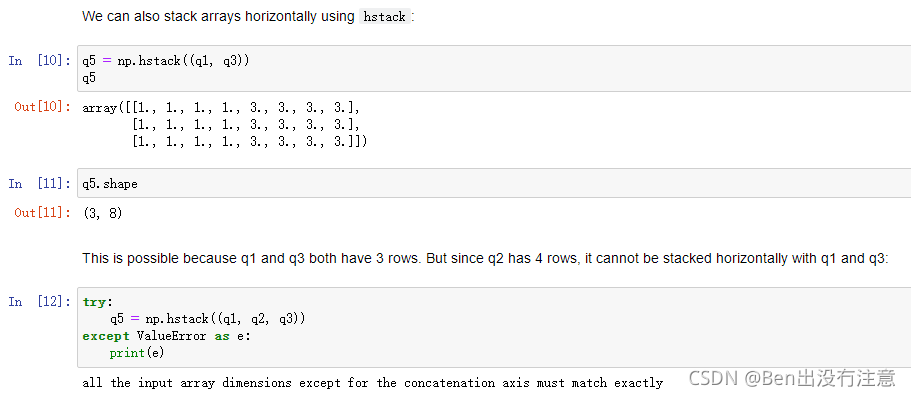
np.hstack
作用:水平叠加(horizontal),相当于往列的方向上增加,前提是行数相同
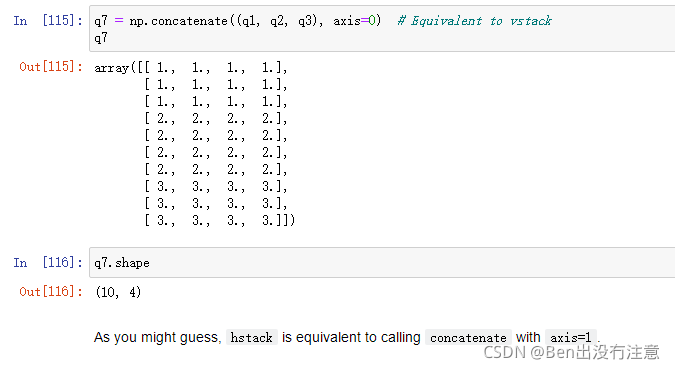
np.concatenate
作用:concatenate沿着任意给定的axis堆叠数组
格式:np.concatenate((ndarray1,ndarray2…),axis=某个轴)
np.stack
stack函数可以沿着一个新的axis堆叠数组,前提是所有数组具有相同的形状。

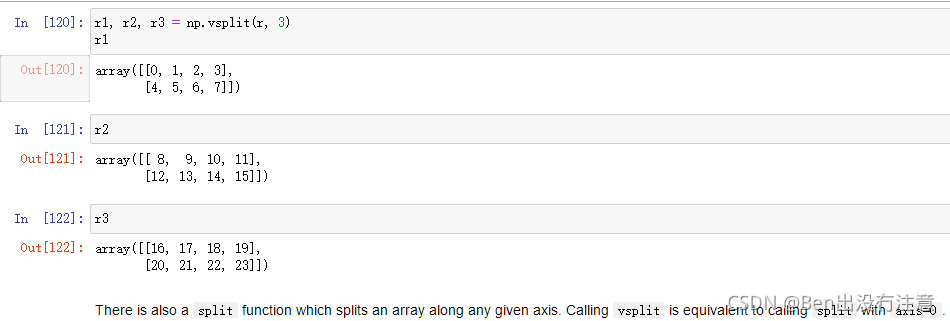
Splitting arrays(分裂数组)
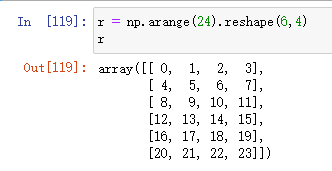
np.vsplit()
作用:垂直split,就是从行划分
np.vsplit(原数组,要划分的个数) = np.split(原数组,要划分的个数,axis=0)
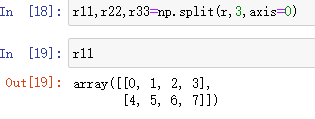
np.hsplit()
作用:水平split,就是从列划分
np.hsplit(原数组,要划分的个数) = np.split(原数组,要划分的个数,axis=1)

Transposing arrays
np.transpose()
Transpose方法在数组的原数据上创建一个新视图,轴按给定的顺序排列。

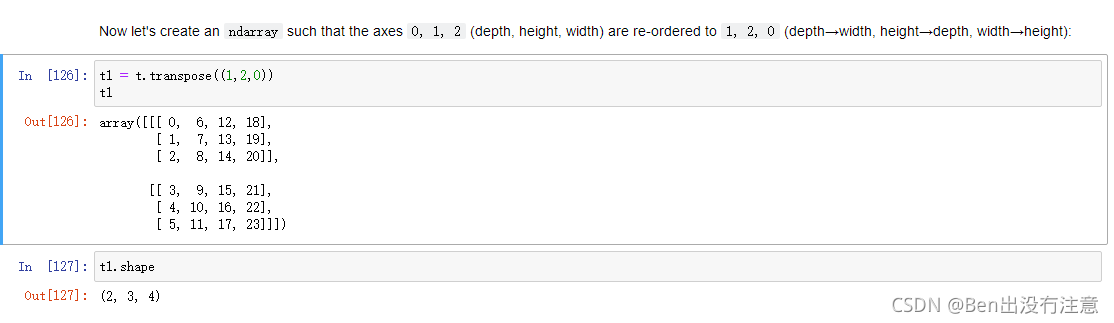
例子中的shape从(4,2,3)变成(2,3,4)。
np.swapaxes()
作用:交换两个axis

Linear algebra(线性代数)
Matrix transpose(矩阵转置)
T 属性相当于当rank大于等于2时调用 transpose() 方法

T 属性对rank =0 或者 rank =1 的数组没有作用。

但是我们可以先通过reshape将1D数组转换为单列的2D数组来得到想要的转置。

Matrix multiplication(矩阵乘法)
np.dot()
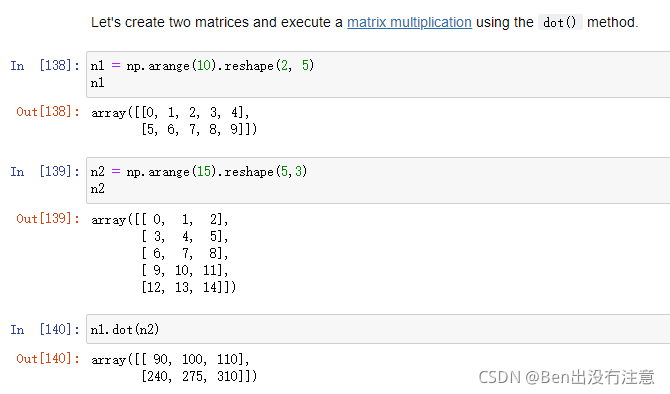
注意:n1*n2不是矩阵乘法,而是一个元素间的乘积,也称为(Hadamard product)
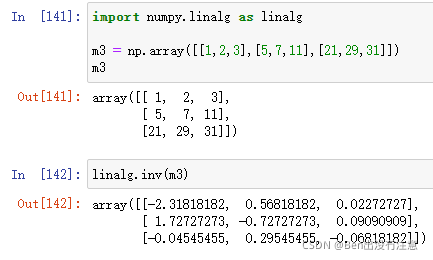
Matrix inverse and pseudo-inverse(矩阵逆与伪逆)
numpy.linalg(linear algebra)
lingalg.inv()
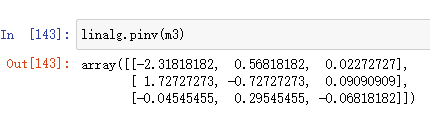
lingalg.pinv()
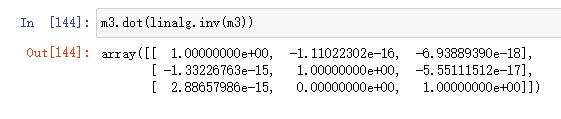
Identity matrix(单位矩阵)
矩阵和逆矩阵的乘积返回一个单位矩阵(带有小浮点数误差):
np.eye(N)
作用:创建一个NxN的单位矩阵
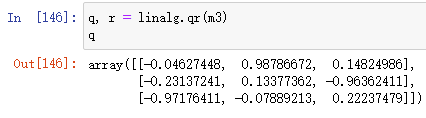
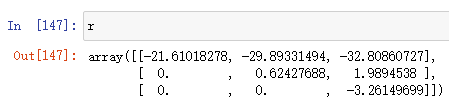
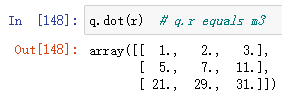
QR decomposition(QR分解)
Determinant(行列式)
形式:linalg.det()

Eigenvalues and eigenvectors(特征值和特征向量)
linalg.eig()
作用:计算矩阵的特征值和特征向量,并返回


Singular Value Decomposition(奇异值分解)
形式:linalg.svd(矩阵)
作用:返回矩阵对应的U,S,V矩阵
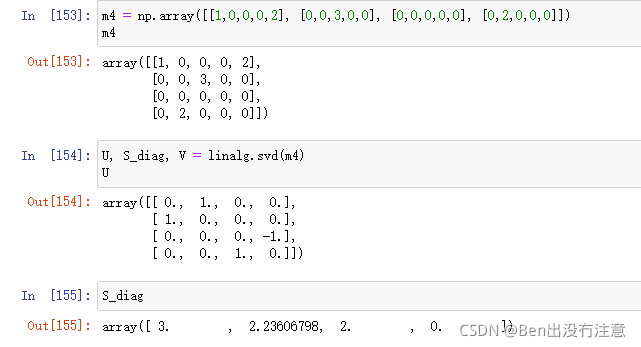
svd函数只返回Σ对角线上的值,但我们想要整个完整的Σ矩阵,所以我们可以创建它。
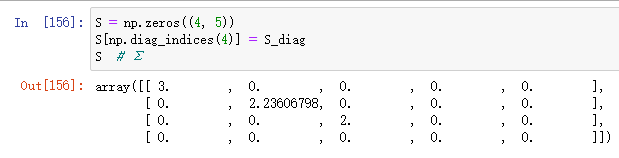

Diagonal and trace(对角线和迹)
形式:np.diag(矩阵)
作用:去矩阵对角线上的元素并返回一个数组

形式:np.trace(矩阵)
作用:返回矩阵的迹,就是对角线上所有元素的和

Solving a system of linear scalar equations(求解线性方程组)
线性方程组ax=b
形式:x = linalg.solve(a,b)
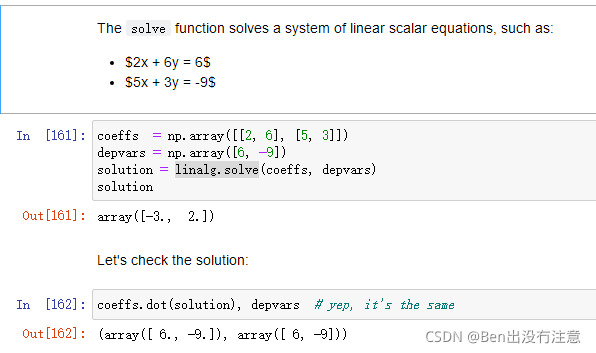
还可以用np.allclose判断两个向量是否相近

Vectorization(向量化)
如果您尝试坚持执行数组操作,那么代码的效率要高得多,而不是对单个数组项一次执行一个操作。这称为矢量化。这样,您就可以从NumPy的许多优化中获益。
例如,假设我们希望根据公式
s
i
n
(
x
y
/
40.5
)
sin(xy/40.5)
sin(xy/40.5)生成一个768x1024数组。一个不好的选择是使用嵌套循环在python中进行计算:

当然,这是可行的,但它的效率非常低,因为循环是在纯python中进行的。让我们把这个算法矢量化。首先,我们将使用NumPy的meshgrid函数,该函数从坐标向量生成坐标矩阵。
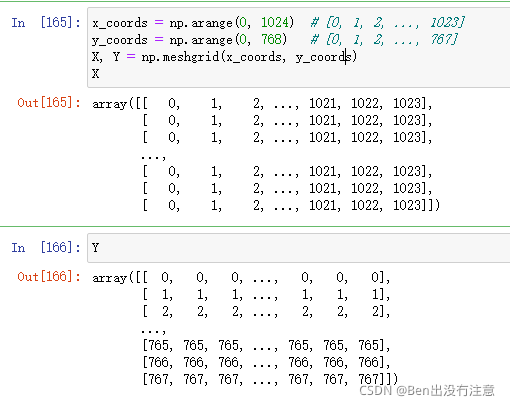
如你所见,X和Y都是768*1024的矩阵,X中的所有值都对应于水平坐标,而Y中的所有值都对应于垂直坐标,

这里的 * 代表的是矩阵中对应元素的相乘
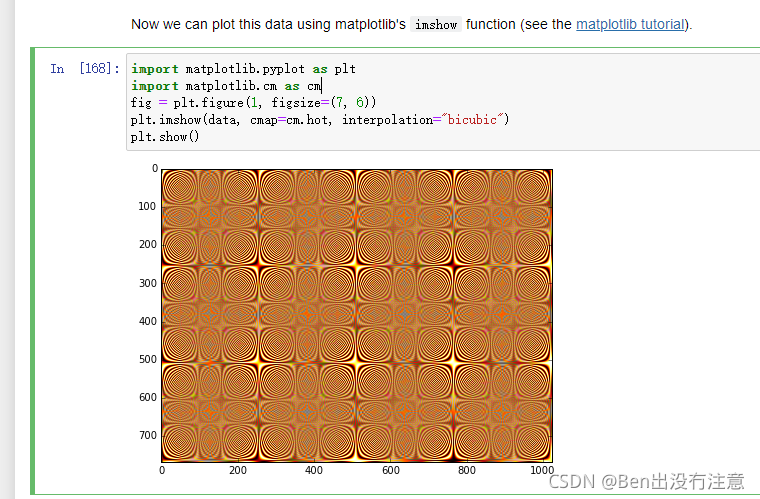
Saving and loading(保存与载入)
Binary .npy format
np.save(路径名,要保存的数组)

如果名字没有包含扩展名,Numpy会自动添加.npy ,同时会默认保存当前工作路径下

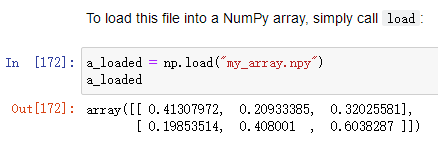
np.load(路径名)
Text format(文本格式)
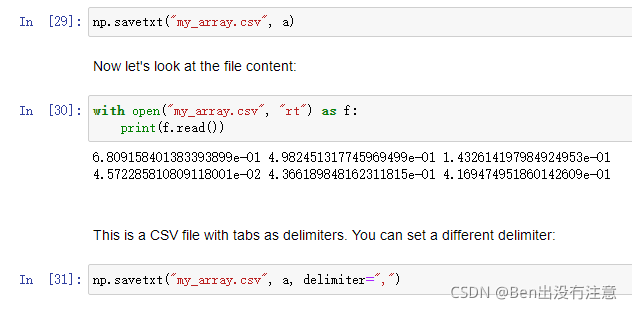
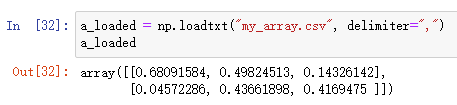
np.savetxt(路径名,要保存的数组,分隔符)
np.loadtxt(要读取的路径,分隔符)
Zipped .npz format
作用:将多个数组保存在一个压缩文件中
np.savez(保存路径,要保存的数组1,要保存的数组2…)
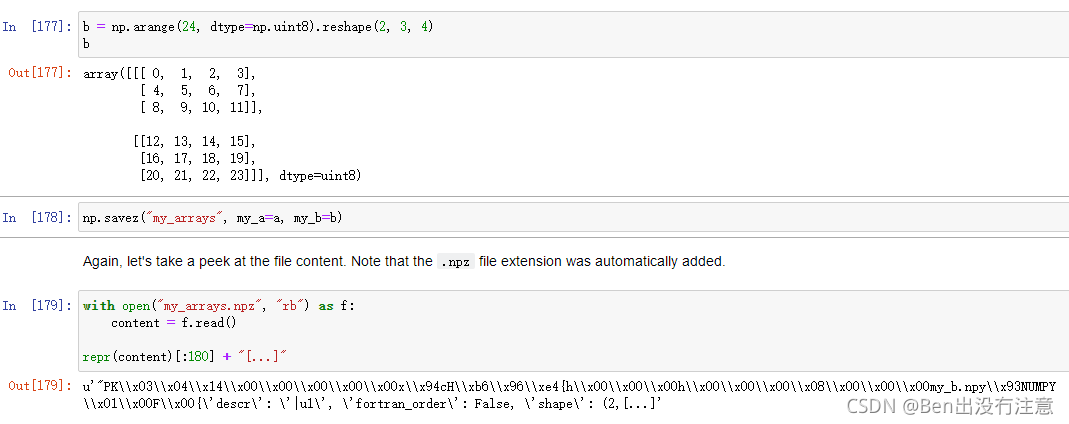
保存的文件扩展名是.npz

读取出来的像字典一样访问