机器学习啃书计划
reference:西瓜书和吴恩达视频
https://github.com/Vay-keen/Machine-learning-learning-notes/blob/master/周志华《Machine%20Learning》
主要还是逼迫自己好好听课!好好总结!
1. 机器学习定义
吴恩达的好胖友prof.Mitchell给出了一个形式化的定义。
假设:P:计算机程序在某任务类T上的性能。
T:计算机程序希望实现的任务类。
E:表示经验,即历史的数据集。
若该计算机程序通过利用经验E在任务T上获得了性能P的改善,则称该程序对E进行了学习。(这里的p可以理解为alphago下棋赢的概率probability提高)
2. 一些术语
所有记录的集合为:数据集。
每一条记录为:一个实例(instance)或样本(sample)。
例如:色泽或敲声,单个的特点为特征(feature)或属性(attribute)
对于一条记录,如果在坐标轴上表示,每个西瓜都可以用坐标轴中的一个点表示,一个点也是一个向量,例如(青绿,蜷缩,浊响),即每个西瓜为:一个特征向量(feature vector)
一个样本的特征数为:维数(dimensionality),该西瓜的例子维数为3,当维数非常大时,也就是现在说的“维数灾难”
所有训练样本的集合为:训练集(trainning set)
所有测试样本的集合为:测试集(test set)
机器学习出来的模型适用于新样本的能力为:泛化能力(generalization),即从特殊到一般。
预测值为离散值的问题为:分类(classification)
预测值为连续值的问题为:回归(regression)
训练数据有标记信息的学习任务为:监督学习(supervised learning),容易知道上面所描述的分类和回归都是监督学习的范畴。
训练数据没有标记信息的学习任务为:无监督学习(unsupervised learning),常见的有聚类和关联规则。
3.模型的选择+评估
我们将学习器对样本的实际预测结果与样本的真实值之间的差异成为:误差(error)。
在训练集上的误差称为训练误差(training error)或经验误差(empirical error)。
在测试集上的误差称为测试误差(test error)。
学习器在所有新样本上的误差称为泛化误差(generalization error)
当学习器把训练集学得“太好”的时候,即把一些训练样本的自身特点当做了普遍特征;同时也有学习能力不足的情况,即训练集的基本特征都没有学习出来。我们定义:
学习能力过强,以至于把训练样本所包含的不太一般的特性都学到了,称为:过拟合(overfitting)。
学习能太差,训练样本的一般性质尚未学好,称为:欠拟合(underfitting)。
在过拟合问题中,训练误差十分小,但测试误差较大;在欠拟合问题中,训练误差和测试误差都比较大。
在现实任务中,我们往往有多种算法可供选择,那么我们应该选择哪一个算法才是最适合的呢?
如上所述,我们希望得到的是泛化误差小的学习器,理想的解决方案是对模型的泛化误差进行评估,然后选择泛化误差最小的那个学习器。但是,泛化误差指的是模型在所有新样本上的适用能力,我们无法直接获得泛化误差。
Assumption:泛化误差假定为测试误差
因此,通常我们采用一个“测试集”来测试学习器对新样本的判别能力,然后以“测试集”上的“测试误差”作为“泛化误差”的近似。显然:我们选取的测试集应尽可能与训练集互斥,下面用一个小故事来解释why:
假设老师出了10 道习题供同学们练习,考试时老师又用同样的这10道题作为试题,可能有的童鞋只会做这10道题却能得高分,很明显:这个考试成绩并不能有效地反映出真实水平。回到我们的问题上来,我们希望得到泛化性能好的模型,好比希望同学们课程学得好并获得了对所学知识"举一反三"的能力;训练样本相当于给同学们练习的习题,测试过程则相当于考试。显然,若测试样本被用作训练了,则得到的将是过于"乐观"的估计结果。
测试集与训练集的划分方法
- 留出法
将数据集D划分为两个互斥的集合,一个作为训练集S,一个作为测试集T,满足D=S∪T且S∩T=?
常见的划分为:大约2/3-4/5的样本用作训练,剩下的用作测试。需要注意:训练/测试集的划分要尽可能保持数据分布的一致性,以避免由于分布的差异引入额外的偏差。
常见的做法是采取分层抽样。同时,由于划分的随机性,单次的留出法结果往往不够稳定,一般要采用若干次随机划分,重复实验取平均值的做法。
- 交叉验证法
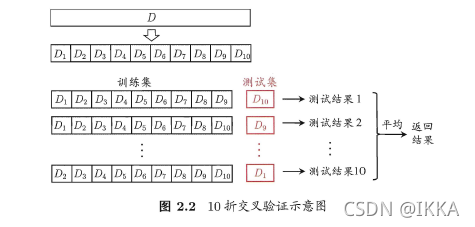
将数据集D划分为k个大小相同的互斥子集,满足D=D1∪D2∪…∪Dk,Di∩Dj=?(i≠j),同样地尽可能保持数据分布的一致性,即采用分层抽样的方法获得这些子集。交叉验证法的思想是:每次用k-1个子集的并集作为训练集,余下的那个子集作为测试集,这样就有K种训练集/测试集划分的情况,从而可进行k次训练和测试,最终返回k次测试结果的均值。交叉验证法也称“k折交叉验证”,k最常用的取值是10。
- 调参
大多数学习算法都有些参数(parameter) 需要设定,参数配置不同,学得模型的性能往往有显著差别,这就是通常所说的"参数调节"或简称"调参" (parameter tuning)。
学习算法的很多参数是在实数范围内取值,因此,对每种参数取值都训练出模型来是不可行的。常用的做法是:对每个参数选定一个范围和步长λ,这样使得学习的过程变得可行。例如:假定算法有3 个参数,每个参数仅考虑5 个候选值,这样对每一组训练/测试集就有555= 125 个模型需考察,由此可见:拿下一个参数(即经验值)对于算法人员来说是有多么的happy。
最后需要注意的是:当选定好模型和调参完成后,我们需要使用初始的数据集D重新训练模型,即让最初划分出来用于评估的测试集也被模型学习,增强模型的学习效果。用上面考试的例子来比喻:就像高中时大家每次考试完,要将考卷的题目消化掉(大多数题目都还是之前没有见过的吧?),这样即使考差了也能开心的玩耍了~。