[人工智能]随机网络模型

要理解网络结构与网络行为之间的关系并进而考虑改善网络的行为，就需要对实际网络的结构特征有很好的了解，并在此基础上建立合适的网络拓扑模型。

一、从规则网络说起

1、常见规则网络

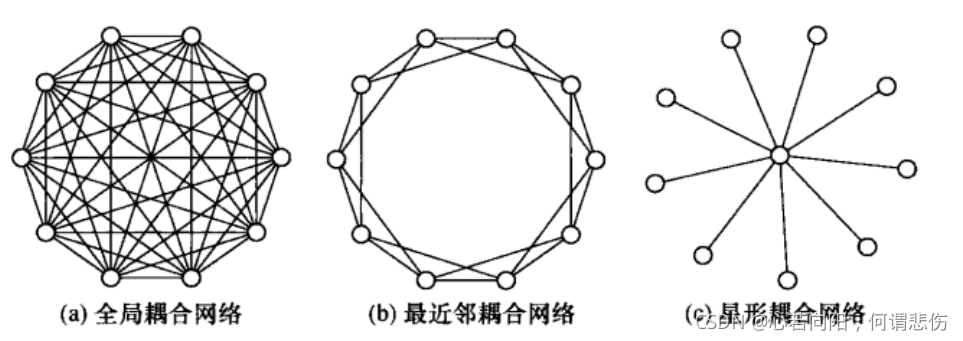
上图中显示了3中规则网络：全局耦合网络、最近邻耦合网络、星形耦合网络。下面我们来一一介绍。

1.1 全局耦合网络

如果一个网络中任意两个节点之间都有边直接相连，那么就称该网络为一个全局耦合网络，简称全耦合网络。
但在实际中一个大规模的全耦合网络维护起来非常困难，例如我们在学校，不可能所有人都认识，也不可能什么都不干，每天去认识人。这也反映了全耦合网络作为实际网络模型的局限性：大型实际网络一般都是稀疏的，它们的边的数目一般至多是O(N)，而不是O(N${}^2$)。
另一方面，尽管从全局看大规模实际网络具有稀疏性，但是，网络中可能会存在不少稠密的甚至是全耦合的子图。

1.2 最近邻耦合网络

如果在一个网络中，每一个节点只和它周围的邻居节点相连，那么就称该网络为最近邻耦合网络。这是一个得到大量研究的稀疏的规则网络模型。
上图（b）是常见的一种具有周期边界条件的最近邻耦合网络包含围成一个环的N个节点，其中每个节点都与它左右各K/2各邻居点相连，这里K是一个偶数。

1.3 星形耦合网络

这是另外一个常见的规则网络，它有一个中心点，其余的N-1个点都只与这个中心点连接，而它们彼此之间不连接。这个模型也可推广到具有多个中心的情形。

2、基本拓扑性质

2.1 全耦合网络

N个节点构成的全耦合网络中有N(N-1)/2条边。在具有相同节点数的所有网络中，全耦合网络具有最多的边数、最大的聚类系数C${}_{gc}$=1和最小平均路径长度L${}_{gc}$=1。

2.2 最近邻耦合网络

（1）聚类系数：我们采用基于网络中三角形数量的聚类系数的定义来计算上图（b）所示的最近邻耦合网络的聚类系数。假设N充分大，K是一个与N无关的常数并且K<<N。首先注意到这样一个事实：网络中任意一个三角形都可以看作是从一个节点出发，先沿着同一个方向走两条边，然后再沿着反方向走一条边形成的。由于反方向的边的最大跨度为K/2，从一节点出发的三角形的数量就等于从K/2个节点中选取两个节点的组合数，即为

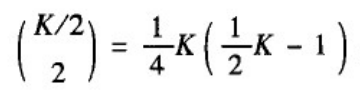
另一方面，网络中任意一个节点为中心的连通三元组的数目为：

于是，最近邻耦合网络的聚类系数为：


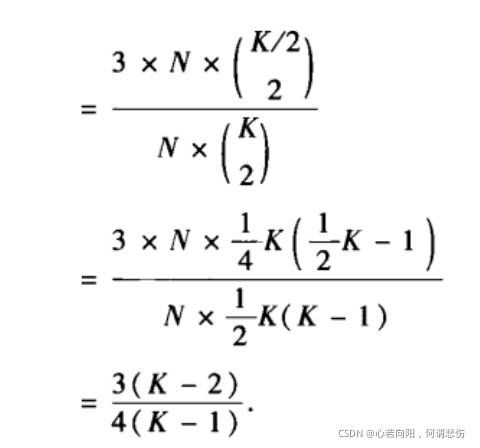
（2）平均路径长度：网络中一个节点能在一步到达的最远的节点与该节点的格子间距为K/2。两个格子间距为m的节点之间的距离为$?$ 2m/K $?$，即不小于 2m/K的最小整数。该网络的平均路径长度为：

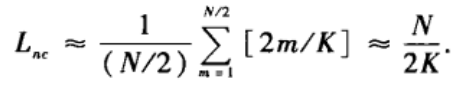
对固定的K值，当N->$\infty$时，L${}_{nc}$->$\infty$。这可以从侧面解释为什么在这样一个局部耦合的网络中很难实现需要全局协调的动态过程。

2.3 星形网络

聚类系数：C${}_{star}$=0。
这是因为中心节点的N-1个邻居节点之间互不相连，从而中心节点的聚类系数也为0。
平均路径长度：

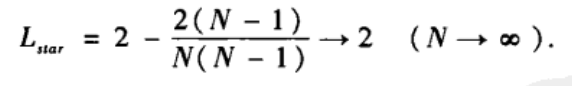
二、随机图

1、模型描述

与完全规则网络相对应的是完全随机网络，最为经典的模型是ER随机图模型。该模型既易于描述又可通过解析方法研究。
ER随机图具有两种形式的定义：

1.1 具有固定边数的ER随机图G（N,M）

ER随机图G（N,M）构造算法：
（1）初始化：给定N个节点和待添加的边数M。
（2）随机连边：
1）随机选取一对没有边相连的不同的节点，并在这对节点之间添加一条边。
2）重复步骤1），直至在M对不同的节点对之间各添加了一条边。
从另一个等价的角度看，该模型是从所有的具有N个节点和M条边的简单图中随机地选取出来的。正是由于随机性的存在，尽管给定了网络中的节点数N和边数M，如果在计算机上重复做两次实验，生成的网络一般也是不同的。因此，严格来说，随机图模型并不是指随机生成的单个网络，而是指一簇网络。G（N,M）的严格定义是所有图G上的一个概率分布P(G)：记具有N个节点和M条边的简单图的数目为$\Omega$，那么对于任一这样的简单图有P(G)=1/$\Omega$，而对于任一其他图有P(G)=0。
在讨论随机图的性质时，通常是指这一簇网络的平均性质。例如，G（N,M）的直径是指该簇网络直径的平均值，即有：

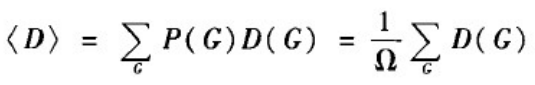
其中D（G）为图G的直径。
采用这种“平均化”的合理性：许多网络模型的度量值的分布都具有显著的尖峰特征，当网络规模变大时越来越聚集在这簇网络的平均值附近。因此，当网络规模趋于无穷时，绝大部分的度量值都会与均值非常接近。

1.2 具有固定连边概率的ER随机图G(N,p)

在模型G(N,p)中不固定总的边数，而是把N个节点中任意两个不同的节点之间有一条边的概率固定为p，构造算法如下：
（1）初始化：给定N个节点以及连边概率p$\in$[0,1]。
（2）随机连边：
1）：选择一对没有边相连的不同的节点。
2）：生成一个随机数r$\in$(0,1)。
3）：如果r<p，那么在这对节点之间添加一条边；否则就不添加边。
4）：重复步骤1）到3），直至所有的节点对都被选择过一次。
上述算法生成的随机图具有如下几种情形：
（1）如果p=0，那么G(N,p)只有一种可能：N个孤立节点，边数M=0。
（2）如果p=1，那么G(N,p)也只有一种可能：N个节点组成的全耦合网络，边数M=$\frac{1}{2}$N(N-1)。
（3）如果p$\in$（0，1），那么从理论上说，N个节点生成具有任一给定的边数M$\in$[0,$\frac{1}{2}$N(N-1)]的网络都是有可能的。

2、拓扑性质

2.1 边数分布

给定网络节点数N和连边概率p，生成的随机图恰好具有M条边的概率为标准的二项分布：

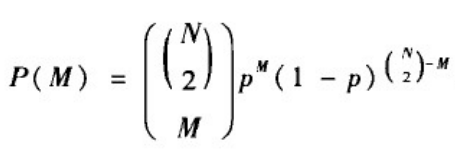
其中，

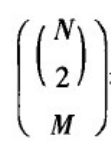
表示具有N个节点和M条边的简单图的数量；

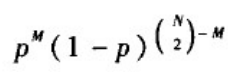
表示有M对节点之间添加了边，

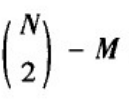
对节点之间没有添加边。
边数分布的平均值：

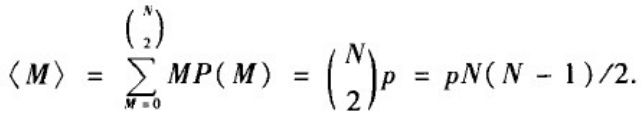
这一结果其实是自然的：N个节点可以组合成N(N-1)/2个节点对，而每个节点对之间存在边的概率都为p。
边数分布的方差：

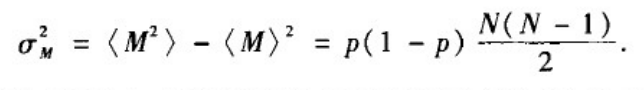
方差刻画了实际生成模型的边数围绕均值< M >的波动大小。进一步的，为了消除由于网络参数不同而导致边数的均值不同所带来的影响，可以用统计学中的变异系数来刻画所生成的网络边数偏离均值< M >的程度。
边数分布的变异系数：

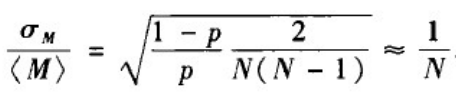
可以看到，对于任意给定的连边概率p$\in$[0,1]，当网络规模增大时，边数分布也变得越来越窄，也就越能确信仿真生成的模型中的边数越接近均值< M >=pN(N-1)/2。
随机图的稀疏性：如果连边概率p与1/N同阶，即p=O（1/N），那么有：

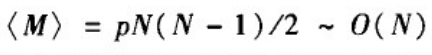
这意味着当网络规模充分大时所得到的ER随机图为稀疏网络。

2.2 度分布

网络中任意给定节点恰好与其它k个节点有边相连的概率为p${}^k$(1-p) ${}^{N?1?k}$，由于共有$\left(\genfrac{}{}{0ex}{}{N?1}{k}\right)$种选取这k个其它节点的方式，因此网络中任一给定节点的度为k的概率同样服从二项分布：

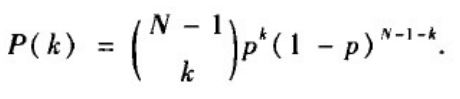
度分布的均值：

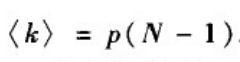
这一结果也是自然的：网络中任一节点与其它N-1个节点中的每个节点有边相连的概率都为p。
度分布的方差：

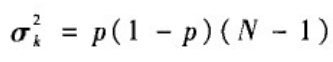
度分布的变异系数：

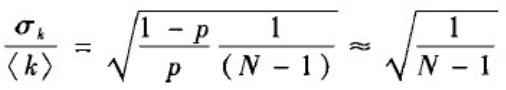
同样可以看到，对于任意给定的连边概率p$\in$[0,1]，当网络规模增大时，度分布也变得越来越窄，也就能确信仿真生成的模型中各节点的度越接近均值< k >=p(N-1)。
泊松分布：当N很大且p很小时，有

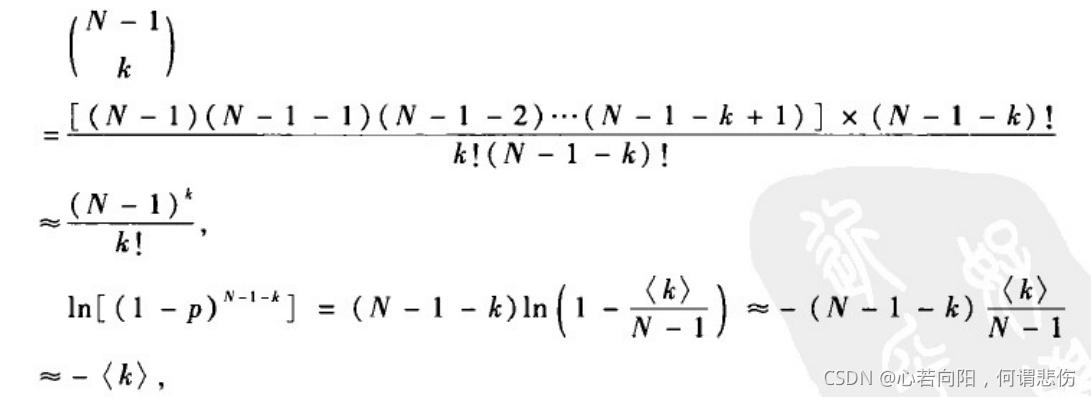
从而有：

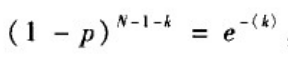
于是二项分布可近似为泊松分布，即有

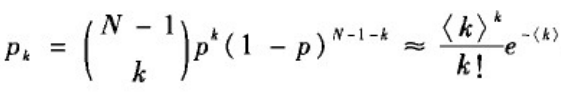
在固定平均度< k >的情形，当N很大时，p=< k >/(N-1)变得非常小。因此，ER随机图也称为泊松随机图。

2.3 聚类系数与平均路径长度

网络中任一节点的聚类系数定义为该节点的任意两个邻居节点之间有边相连的概率。对于ER随机图G(N,p)而言，两个节点之间不论是否具有共同的邻居节点，其连接概率均为p。因此，ER随机图的聚类系数为

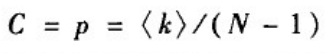
直观上，由于ER随机图的聚类系数很小，意味着网络中的三角形数量相对很少。对于ER随机图中随机选取的一个点，网络中大约有< k >个其他的点与该点之间的距离为1；大约有< k >${}^2$个其他节点与该节点之间的距离为2；以此类推，由于网络总的节点数为N，设D${}_{ER}$是ER随机图的直径，大体上应该有N$～$< k >${}^{D_{ER}}$。因此，网络的直径和平均路径长度满足

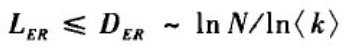
这种平均路径长度为网络规模的对数增长函数的特性就是典型的小世界特征。因为lnN值随N增长得很慢，这就使得即使是规模很大得网络也可以具有很小得平均路径长度和直径。

3、巨片的涌现与相变

3.1 随机图的演化

ER随机图的连通性具有两个极端情形：
（1）p=0对应于N个孤立节点：最大连通片只包含一个节点，与网络规模N无关。
（2）p=1对应于全耦合网络：最大连通片规模为N，随着网络规模的增长而增长。一般而言，如果网络中的一个连通片的规模随着网络规模的增长而成比例增长，那么该连通片就是一个巨片，因为当网络规模充分大时，这个巨片会包含网络中相当比例的节点。
直观上看，随着连边概率p的增加，生成的随机图中的边数也在增加，网络的连通性也越来越好。现在的问题是当连接概率p从0开始逐渐增加到1时，最大连通片的规模是如何具体变化的呢？特别的，当p多大时才会出现包含网络中一定比例节点的巨片。

3.2 巨片的涌现

前人们系统地研究了当N->$\infty$时ER随机图的性质(包括巨片的出现)与概率p之间的关系。特别的，他们发现ER随机图具有如下的涌现或相变性质：ER随机图的许多重要性质都是突然涌现的：对于任一给定的连边概率p，要么几乎每一个G(N，p)的实例都具有某个性质Q。要么几乎每一个这样的图都不具有性质Q。
这里，如果当N->$\infty$时产生一个具有性质Q的ER随机图的概率为1，那么就称几乎每一个ER随机图都具有性质Q。
当N->$\infty$时ER随机图的巨片的相对规模S$\in$[0,1]定义为巨片中所包含的节点数占整个网络节点的比例，即一个随机选择的节点不属于巨片的概率。u=1-S为不属于巨片的节点所占的比例。显然，存在如下两种可能：
（1）网络中不存在巨片，即S=0，u=1；
（2）网络中存在巨片，即S>0，u<1。
网络中一个随机选择的节点i如果不属于巨片，那么就说明它也没有通过q其他任一节点与巨片相连，也即对于网络中的其他任一节点j，必然有如下两种情形之一：
（1）节点i与节点j之间没有边相连：此情形发生的概率为1-p。
（2）节点i与节点j之间有边相连，但是节点j不属于巨片：此情形发生的概率为pu。
因此，节点i没有通过任一节点与巨片相连的概率为：

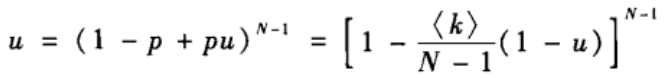
对上式两边取对数，有

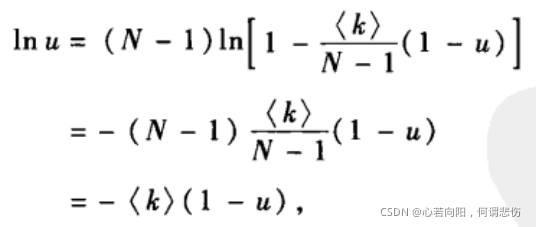
从而

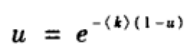
于是可以得到巨片中节点的比例S=1-u满足

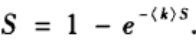
上式尽管看上去简单，却不存在简单的解析解。

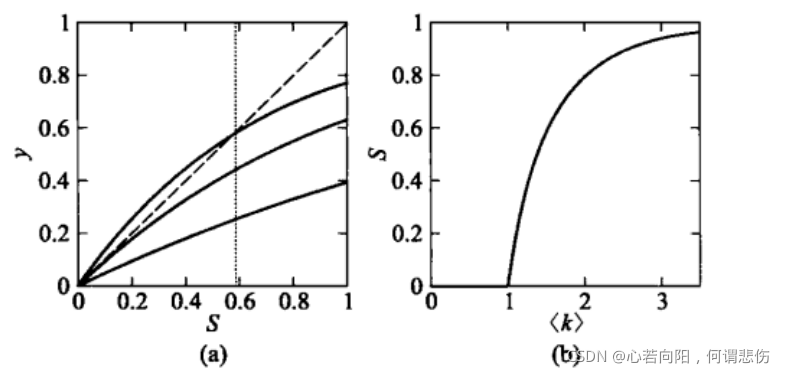
上图绘制了平均度< k >取0.5、1、1.5上式三种情形的曲线。图中的虚线是y=S，当< k >小于1时只有一个交点，当< k >大于1时还有另外一个交点。基于以下交点，可以得到网路平均度和巨片规模的关系如上图中的（b）所示。
可以看到，在< k >小于1时，S=0意味着不存在巨片；在< k >大于1时，S>0意味着涌现巨片。临近点< k >${}_c$=1也可通过下式得到：

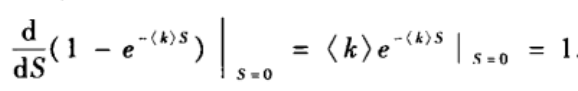
由于ER随即图的平均度是< k >=p（N-1）$\approx$ pN，从而产生巨片的连边概率p的临界值为

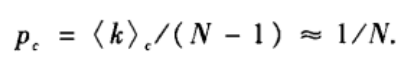
即当p>p${}_c$时，几乎每一个随机图都包含巨片。

4、随机图与实际网络的比较

4.1 共性特征

ER随机图与许多实际网络相比具有如下一些共性特征：
（1）稀疏性。实际网络往往是稀疏的，而当连边概率p与网络规模的倒数同阶（p$～$ O(1/N))时，ER随机图是一个边数与网络规模同阶的稀疏图，M$～$ 0(N)。
（2）有巨片。实际网络往往存在巨片，当p>p${}_c～$ 1/N时，ER随机图具有一个包含网络中相当比例节点的巨片。
（3）小世界。ER随机图的平均距离大体上是网络规模的对数函数，L$～$InN/ln< k >，而实际网络往往也具有与相同规模和密度的ER随机图相近的平均距离。

4.2 不同特征

但是，ER随机图也具有一些与实际网络显著不同的特征。
（1）聚类特性的差异。对于固定的网络密度，当N→∞时，ER随机图的聚类系数C${}_{ER}$=< k >/(N-1)->0，意味着ER随机图没有聚类特性。例如，假设全世界70亿人组成的社会网络近似具有ER随机图结构，那么即使平均每人有1000个朋友，网络的聚类系数也会非常小(C$\approx$ 10${}^{?7}$)。实际网络却往往具有明显的聚类特性，它们的聚类系数比相同规模的ER随机图的聚类系数高得多。
（2）度分布的差异。ER随机图的度分布近似服从均匀的泊松分布，意味着网络中节点的度基本都集中在平均度< k >附近。另一方面，实际网络的度分布往往具有较为明显的非均匀特征：网络中会存在少量度相对很大的节点，从而意昧着网络度分布与均匀的泊松分布有显著偏离。

三、广义随机图

1、配置模型

人们可以从多个角度对ER随机图进行扩展以使其更接近实际网络。其中一个自然的推广就是具有任一给定度分布、但在其它方面完全随机的的广义随机图。到目前为止研究最多的广义随机图模型是配置模型。在配置模型中事先给定的是网络的度序列{d${}_1$，d${}_2$，，，d${}_N$}，其中非负整数d${}_i$为节点i的度。显然，度序列并不能完全任一给定，否则有可能无法生成符合度序列的简单图。两个显而易见的必要条件是：
（1）由于网络中所有节点的度值之和等于网络中所有边数的度值之和的两倍，${\sum }_{i=1}^N$d${}_i$必须为偶数并且有：

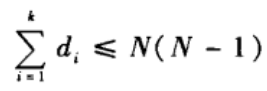
（2）d${}_i$<=N-1，i=1，2，，，N，等号只有当一个节点与其它所有的节点都相连时才能成立。
在上述条件的基础上少许加以推广，就可得到如下的充要条件：
**定理：**一个非负整数序列{d${}_1$，d${}_2$，，，d${}_N$}是某个简单图的度序列的充要条件为：
（1）${\sum }_{i=1}^N$d${}_i$为偶数。
（2）对于每个整数k，1<=k<=N，均有

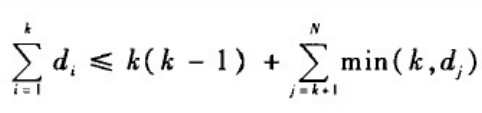
例如，验证整数序列{6，6，5，4，4，2，1}是否为某个简单图的度序列如下：

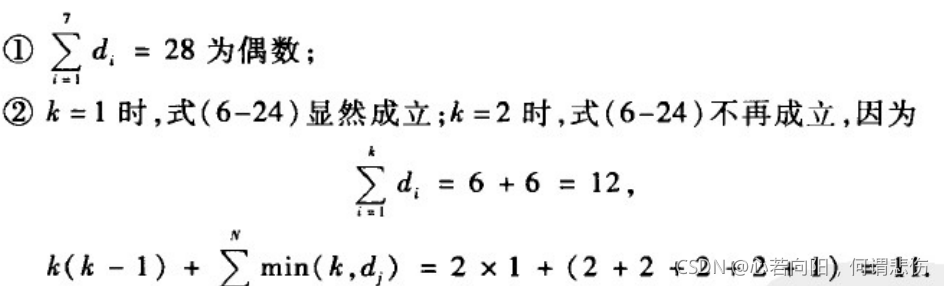
所以，上述整数序列不可能为某个简单图的度序列。
另一种给定度序列的等价方法是给定网络中度为k的节点数目。n（k），k=0，1，2，，，k${}_{max}$。网络的节点数N和边数M满足

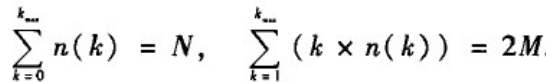
生成具有给定度序列的广义随即图的配置模型算法如下：
（1）初始化：根据给定度序列确定N个节点的度值。
（2）引出线头：从度为k${}_i$的节点i引出k${}_i$。共有${\sum }_{i=1}^N$k${}_i$=2M个线头，M为网络的边数。
（3）随机配对：完全随机的选取一对线头，把他们连在一起，形成一条边；再在剩余的线头中完全随机地选取另一对线头连成一条边；以此进行下去，直至用完所有的线头。
关于配置模型算法的几点说明：
（1）度序列应满足的条件。由于任一无向网络中所有节点的度之和${\sum }_i$k${}_i$必然为偶数，因此，给定的度序列也必须满足这一条件。
（2）生成具有给定度分布的网络。我们可以首先基于该度分布生成一组度序列，然后再利用上述配置模型算法。
（3）等概率随机配对。配置模型算法中的任意两个线头之间相连的可能性都是一样的。正是基于这一特性，我们可以从理论上分析配置模型的一些性质。
（4）生成模型的不唯一性。由于配置模型算法中的随机配对，对于给定的度序列，重复两次实验得到的具有相同度序列的模型在其他方面可能有很大区别。事实上，2M个线头两两配对组成M条边，共有M(2M -1)种可能的配置方案，采用上述生成算法得到其中每一种配置方案的可能性都是一样的。当然，不同的配置方案并不一定对应于不同的网络。例如，下图中所示的包含3个节点的配置方案都是相同的。其中，每个节点旁边的两个字母对应于从该节点引出的两个线头。

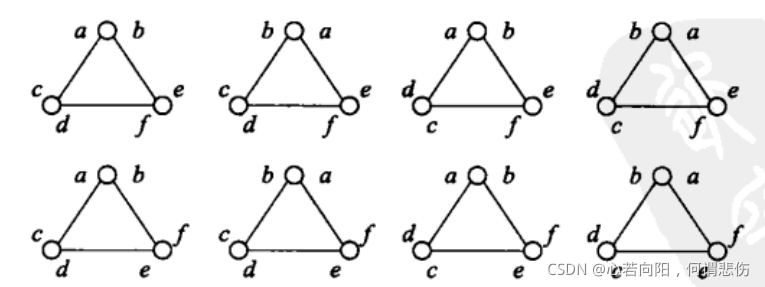
（5）有可能产生自环和重边。我们当然可以在算法中的配对步骤不允许自环和重边，但是这样的话，线头之间的配对就不在是完全随机的了，从而使得难以对该模型做理论分析。

2、配置模型的理论分析

2.1 余平均度

配置模型的一个好处是可以基于该模型从理论上研究一些问题。我们知道，平均度为：

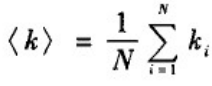
节点的余平均度为：

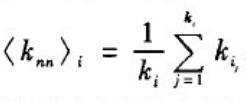
一个给定网络的余平均度定义为网络中每个节点的余平均度的平均值：

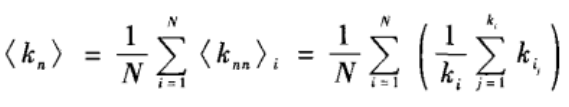
它反映了网络中随机选取的一个节点的邻居节点的平均度。
实际网络中节点的邻居节点的平均度往往大于网络节点的平均度。

2.2 余度分布

我们知道，网络中节点的平均度与度分布之间具有如下关系：

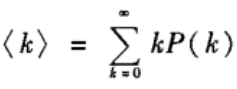
类似的，余平均度也可以通过余度分布来计算

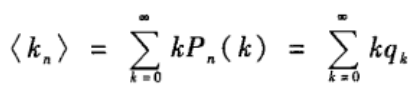
其中，余度分布P${}_n$(k)$\equiv$q${}_k$定义为网络中随机选取的一个节点的随机选取的一个邻居节点的度为k的概率。
现在我们计算配置模型的余度分布。要从一个随机选择的节点及另一个线头产生一条边，我们是从其它2M-1个线头中完全随机地任选一个，然后把这两个线头连在一起形成一条边。由于每个度为k的节点都有k个线头，因此从一个给定节点沿着一条边到达一个邻居节点的度为k的概率为k/(2M-1)$\approx$k/2M。而网络中度为k的节点总数为Np${}_k$，因此一个随机选择的节点与网络中任一度为k的节点有边相连的概率为：

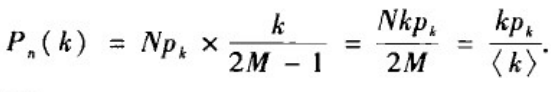
其中利用了2M=N< K >。
上式意味着在给定网络平均度的情形下，从网络中一个随机选择的节点出发，沿着一条边到达一个度为k的邻居节点的概率与kp${}_k$而不是与p${}_k$成正比。也就是说，到达的可能是比一个典型节点的度更高的节点。
基于上式，配置模型中随机选取的一个节点的邻居节点的平均度为：

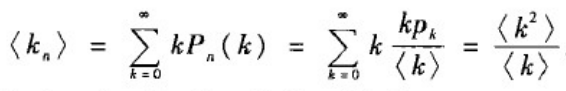
这一结论与对于度不相关网络的到的结论是一致的，于是有：

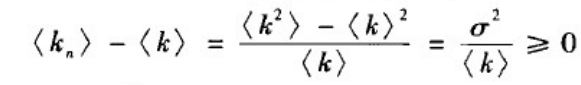
其中，网络度分布的方差${\sigma }^2$总是非负的。事实上，除非网络中的每个节点都有相同的度，否则方差${\sigma }^2$是严格为正的，此时平均度< k >当然也大于0。因而有

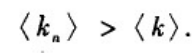
尽管此式子是基于配置模型推导出来的，但是这一结论在许多实际网络任然是成立的。

四、随机模型与零模型

1、零模型

我们把一个实际网络具有相同的节点数和相同的某些性质A的随机网络称为该随机网络的随机化网络。这里的某些性质A可以是平均度、度分布、聚类系数、同配系数等，或者是他们的某种组合。从统计学角度看，“具有性质A的网络G也具有某一性质P”是一个零假设，而为了要验证这一零假设是否成立，就需要有与原网络G具有相同规模和相同性质A的随机化网络作为参考系，以判别性质P是否为这类随机化网络的典型特征。这类随机化网络模型在统计学上称为零模型。
ER随即图可以视为阶数最低的零模型。有时我们需要具有更多约束条件的零模型：
（1）0阶零模型：与原网络具有相同节点数和边数的随机化网络。
（2）1阶零模型：与原网络具有相同节点数和度分布的随机化网络。通常的做法是每个节点的度值都保持不变。
（3）2阶零模型：与原网络具有相同节点数和二阶度相关特性（即联合分布）的随机化网络。有时也考虑与原网络具有相同同配系数的随机化网络。
（4）3阶零模型：与原网络具有相同节点数和三阶度相关特性（即联合边度分布）的随机化网络。

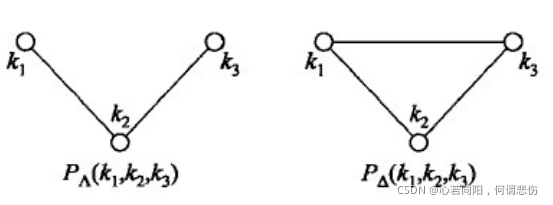
如图所示，3个节点构成的三元组有如下两种情况，因此3阶度相关特性P(k${}_1$,k${}_2$,k${}_3$)是由P${}_{\Lambda }$(k${}_1$,k${}_2$,k${}_3$)与P${}_{\Delta }$(k${}_1$,k${}_2$,k${}_3$)共同组成的。
以此类推，我们还可以定义更高阶的零模型。

上图是一个简单网络及其0到3阶度相关性质。该网络拓扑可由其3阶度相关性质完全表征。
显然，对于一个给定网络G和任意自然数d${}_1$<d${}_2$，具有与网络G相同的d${}_2$阶分布的模型集合一定是与网络G具有相同的d${}_1$阶分布的模型集合的子集，而网络G的d阶零模型的性质就取为与网络G具有相同的d阶分布的模型集合性质的平均。随着d的增大，d阶零模型将越来越接近给定网络G。如下图所示：

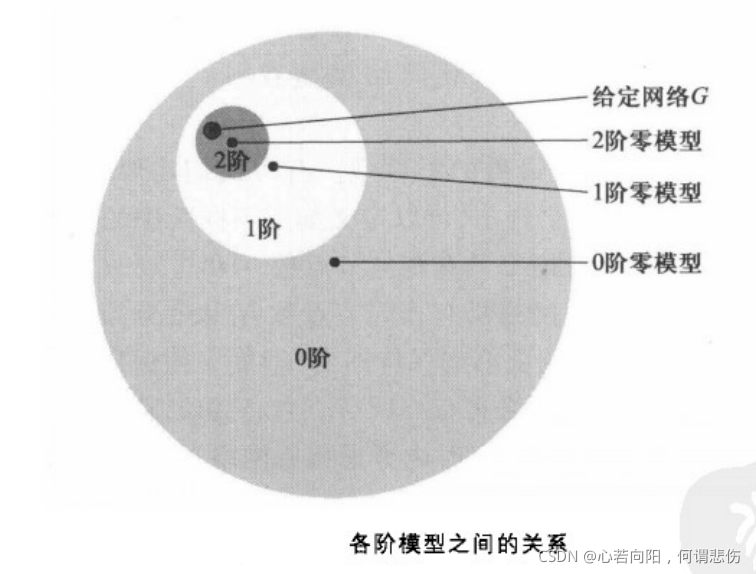
2、随机重连

假设我们已经有了某个实际网络的拓扑数据，其中包含节点之间是如何连接的完全信息(当然也就包含了度序列的信息)。如果要生成一个与这个网络具有相同度序列的随机网络模型，要怎么做？
如果严格要求不允许重边或自环，那么就不能用配置模型算法。因为有限制条件，这个网络的形成也不是完全随机的。这是，就可以在原始网络的基础上，保持每个节点的度不变，但是使得连边的位置尽可能的随机化，以得到一个具有给定度序列的随机网络，此过程所用的算法就是随机重连算法。

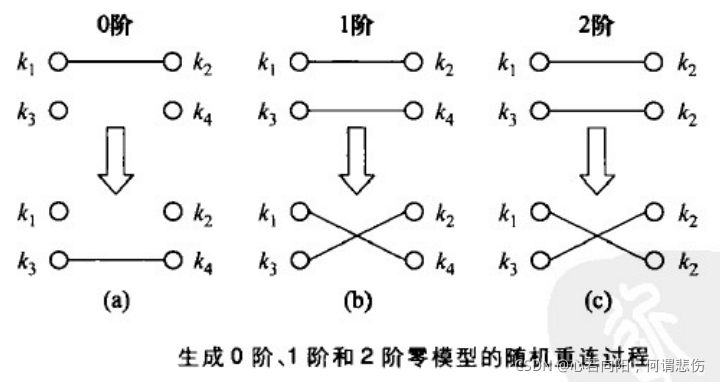
（1）生成0阶零模型的随机重连算法。每次随机取出原网络中的一条边k${}_1$k${}_2$，再随机选择网络中两个不相邻的节点k${}_3$和k${}_4$，并在他们之间添加一条连边k${}_3$k${}_4$。重复此过程充分多次。
（2）生成1阶零模型的随机重连算法。每次随机选择原网络中的两条边，记为k${}_1$k${}_2$和k${}_3$k${}_4$如果k${}_1$、k${}_2$、k${}_3$、k${}_4$这四个节点之间只有这两条边，那么就去除这两条边，并将节点k${}_1$和k${}_4$相连，k${}_2$和k${}_3$相连。从而得到两条新边k${}_1$k${}_4$和k${}_2$k${}_3$。注意到这4个节点的度值均保持不变，故网络的度序列仍保持不变。重复此过程充分多次。
（3）生成2阶零模型的随机重连算法。对应于保持联合度分布不变，每一步采取与1阶零模型相同的步骤，只是多了一个限制，即要求节点k${}_2$与k${}_4$具有相同的度值。显然，由于这一限制，使得重连得可能性也小了。重复此过程充分多次。
随着零模型阶次的增加，约束条件进一步加强，重连的可能性会不断减小，生成网络的随机化程度也逐渐降低。
上述随机重连算法也可以推广到有向图。

五、基于零模型的拓扑性质分析

1、比较判断

在前面介绍网络的社团结构分析时叙述过，基于模块度的社团检测算法的基本想法就是把待研究的网络与具有相同度序列的一阶零模型做比较，以判断划分的社团结构是否最优。一般而言，基于零模型研究网络特征时需要明确两点：
（1）确定零模型。根据所要研究的特征，确定合适的保持低阶特征不变的零模型。例如要研究的是度相关性(属于二阶特征)，那么就可以选择保持度分布或度序列(一阶特征)不变的一阶零模型。
（2）确定比较方法。把实际网络的特征与相应的零模型做比较。具体的说，假设某种拓扑性质在一个实际网络中出现的次数为N(j)，在相应的随机化网络中出现次数的平均值为< N(j) >，那么可以计算如下比值：

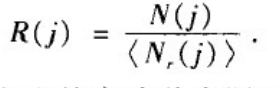
如果R(j)>1（或R(j)<1），那么就意味着实际网络的设计或者演化过程促进（或抑制）了该拓扑特征的出现。
如果要进一步刻画某个拓扑模式在实际网络中出现的频率与相应随机化网络中出现的频率的差异是否显著，那么可以采用统计学中的Z检验方法。具体的说，拓扑性质j的统计重要性可用如下的Z值来刻画：

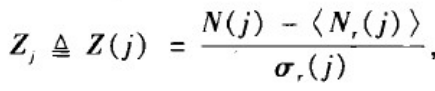
其中，${\sigma }_r$(j)为随机化网络中拓扑性质j的出现次数N${}_r$(j)的标准差。Z值得绝对值越大就表示差异越显著。
通常得做法是在平面上绘制出比值R和Z值的图形，称为相关性剖面。为了便于比较不同规模的网络，通常对Z值做归一化处理，得到重要性剖面：

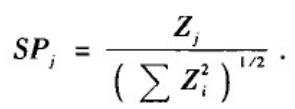
2、度相关性分析

网络的联合概率分布可以表示为：

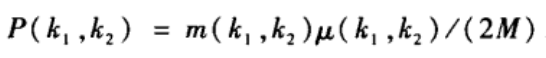
其中m(k${}_1$,k${}_2$)是度为k${}_2$的节点和度为k${}_2$的节点之间的连边数。如果k${}_1$=k${}_2$，那么$\mu$(k${}_1$,k${}_2$)=1。
我们可以通过比较一个实际网络的m(k${}_1$,k${}_2$)及其相应的1阶零模型所对应的均值< m(k${}_1$,k${}_2$) >来分析实际网络的度相关性。具体的说，可以计算并绘制如下的相关性剖面：


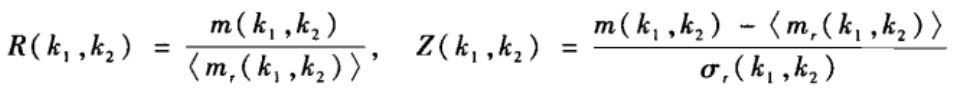
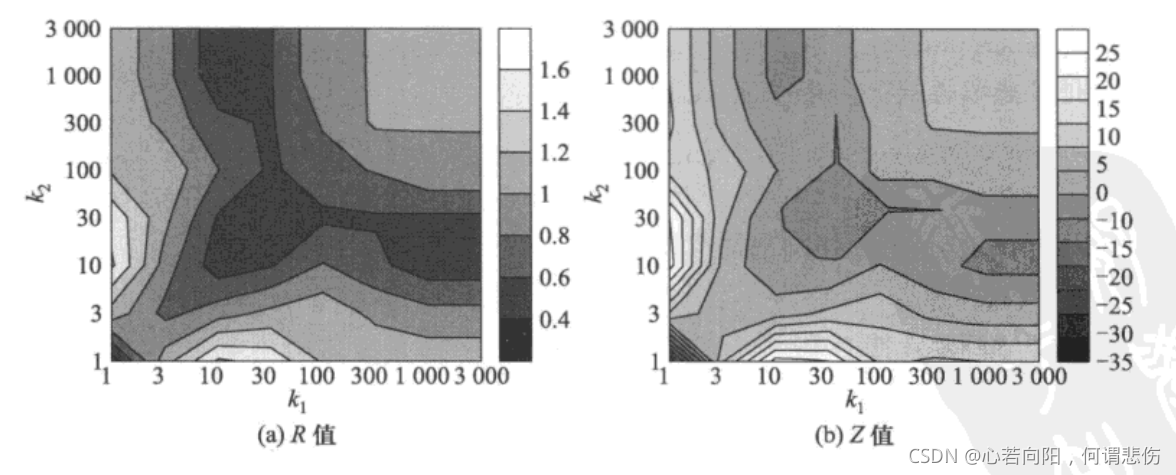
上图显示的是双对数坐标下的互联网拓扑的相关性剖面，该图反映了互联网拓扑演化的如下特征：
（1）小度（k${}_1$<=3,k${}_2$>=1）之间的的连边受到很强的抑制，R值和Z值趋于最小。
（2）中度节点（k${}_1$<100,k${}_2$>=10）之间的连边也受到抑制，R值和Z值都比较小。
（3）小度节点（1<=k${}_1$<=3）与中度节点（10<=k${}_2$<100）之间的连边数量显著增强，R值和Z值都趋于最大。
（4）度最大的5个节点（k${}_1$，k${}_2$>300）中的任意两个节点之间都有一条边。在典型的一阶随机化网络中也具有这一特征，因此，R值接近1而Z值接近0。

3、模体分析

零模型的另一个典型应用是网络的模块化分析，在实际网络中，并非所有的子图都具有相同的重要性。
实际网络可能包含各种各样的子图，其中一些子图所占的比例明显高于相应的零模型中这些子图所占的比例，这些子图称为模体，辨识出模体有助于识别网络的典型局部连接模式。
为了判断实际网络中的一个子图j是否为模体，可以比较该子图在实际网络中出现的次数N(j)与在相应的随机化网络中出现次数的平均值< N${}_r$(j) >，一般要求

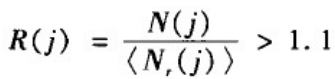
此外，在具体操作时可进一步要求：
（1）该子图在与该实际网络对应的随机化网络中出现的次数大于它在实际网络中出现次数的概率是很小的，通常要求这个概率小于某个阈值P；
（2）该子图在实际网络中出现的次数N(j)不小于某个下限U。

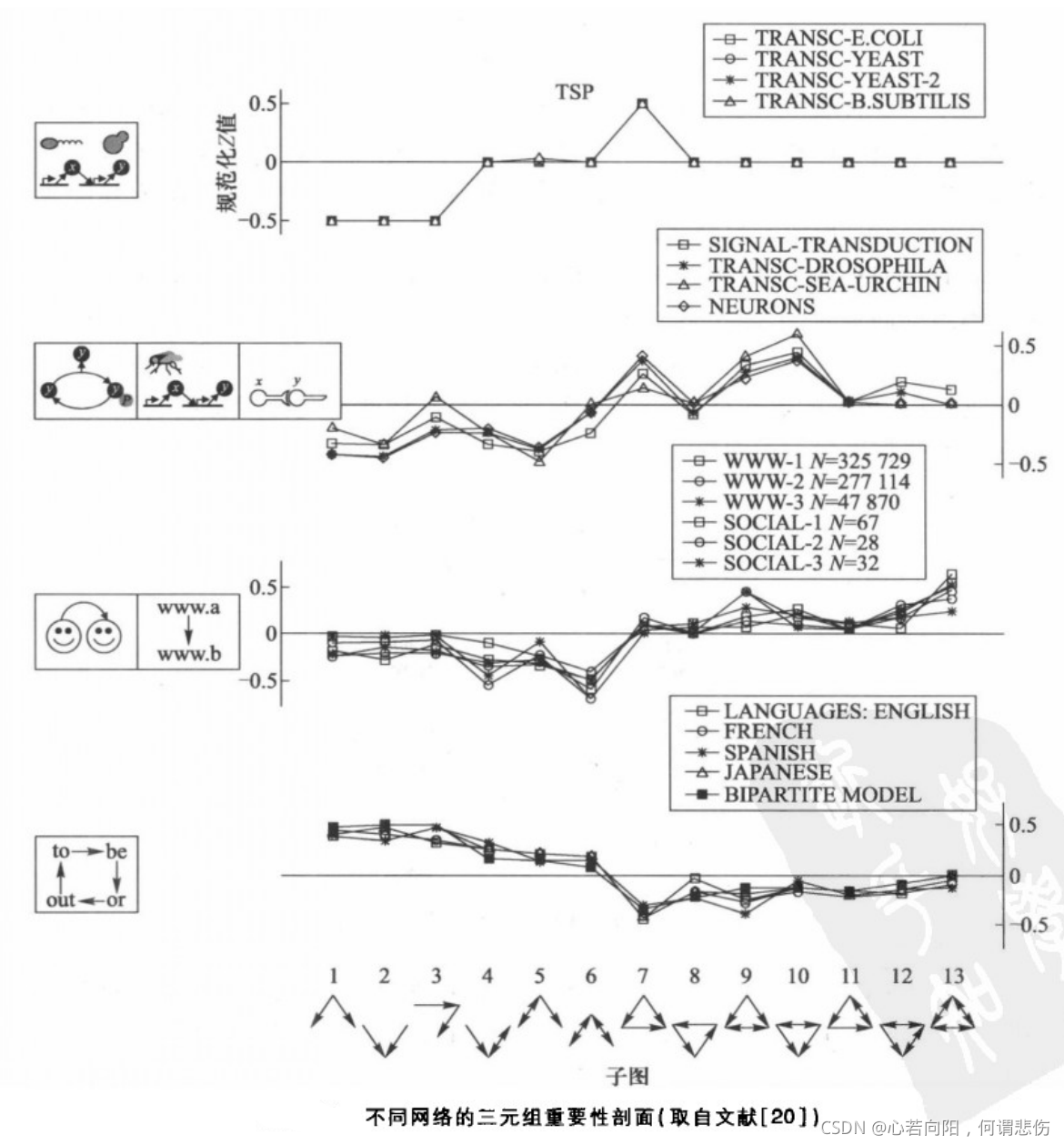
网络中每个子图j的统计重要性可通过重要性剖面来刻画。上图给出了取自不同领域的19个有向网络中包含的所有可能的13个三元组要性剖面(TSP)，它们反映了这13个三元组在网络中的相对重要性。这样就可以根据TSP对网络进行分类，具有相似TSP的网络组成一个网络超家族。从上图可以清楚地看出，19个不同领域的实际网络组成了4个网络超家族。

4、同配性质分析

前面基于零模型我们分析了无向网络的度相关性，现在再进一步基于零模型分析有向网络的度相关性。
前面的文章中讲过，无向网络的度同配性质反映了度值相近的节点之间互相连接的倾向性，它可以用如下的同配系数来表征：

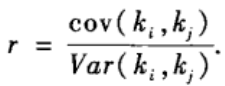
r>0对应于同配，r<0对应于异配。一般而言，同配系数的大小是与网络规模和密度相关的。因此，一种更为合理的评价是把一个实际网络的同配系数与相应的零模型的同配系数做比较以判断网络的同配或异配程度。

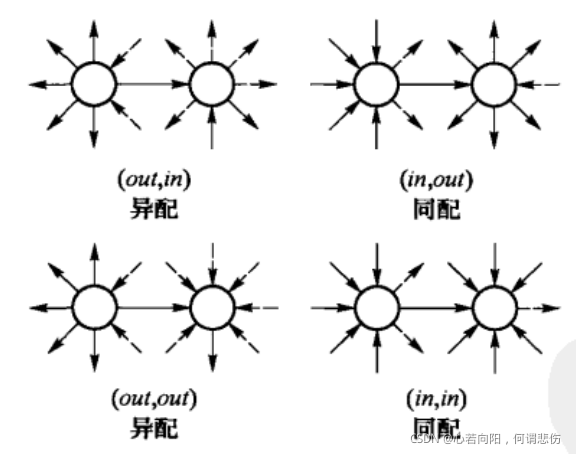
在有向网络情形，边的方向有可能对网络的同配性质产生重要影响。一个有向网络的同配性可以有如下4种度量：r（out，in），r（in，out），r（out，out）和r（in，in）。其中，r（out，in）量化的是高出度的节点有边指向高入度的节点的倾向性程度，其余三种的定义类似。上图为有向网络的4种度相关性。
我们用$\alpha ,\beta \in$[in,out]标记出度或者入度类型，并把有向边i的源节点和目标节点的$\alpha$度和$\beta$度分别记为j${}_i^{\alpha }$和k${}_i^{\beta }$。有向网络的一组同配系数可以用如下的Pearson相关系数刻画：

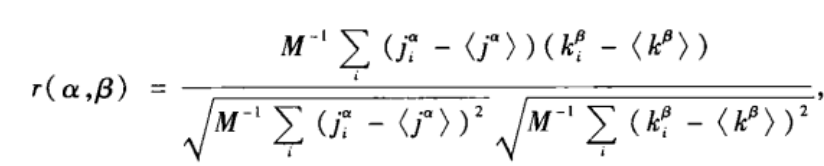
M为网络边数，<*>是平均值。这里规定每种情形下，边都是从$\alpha$标度的节点指向$\beta$标度的节点。
每个相关性r（$\alpha$，$\beta$）的统计重要性可通过Z值来刻画：

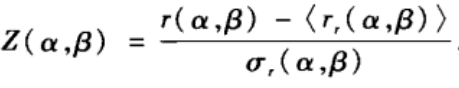
其中< r${}_r$（$\alpha$，$\beta$）>和${\sigma }_r$（$\alpha$，$\beta$）分别为一阶零模型的同配系数的均值和标准差。通常网络规模越大Z值也越大，但我们可以对Z值作归一化处理以消除网络规模的影响，得到如下定义的同配重要性剖面(ASP)：

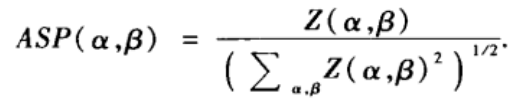
ASP（$\alpha$，$\beta$）>0表明实际网络比具有相同度序列的零模型更为同配，此时称网络是Z同配的；ASP（$\alpha$，$\beta$）<0则表明实际网络比相应的零模型更为异配，此时称网络是Z异配的。