[人工智能]＜机器学习＞＜详解＞ KNN最邻近分类算法

K-Nearest neighbor algorithm

回顾：

Distance measures 的两种方法:

Euclidean distance(本节使用):$D(A,B)=\sqrt{(a_0?b_0{)}^2+(a_1?b_1{)}^2+...+(a_n+b_n{)}^2}$
Manhattan distance:$D(A,B)=|a_1+b_1|+|a_2+b_2|+...+|a_n+b_n|$

Classification Task

属于Supervised Learning的一种。在Supervised Learning中，我们得到了一个Data set，并且已经知道了正确Output应该是什么样子，并且知道Input和Output之间存在关系。

• 监督学习问题分为*“regression”和“classification”*问题
  • Regression Task：我们试图在连续输出中预测结果，这意味着我们试图将输入变量映射到某个连续函数。
  • Classification Task：我们试图在离散输出中预测结果。换句话说，我们试图将输入变量映射到离散函数中。

K-Nearest neighbor algorithm

使用 Nearest neighbor algorithm 需要的已知条件：

1. Test Dataset: 记录所有 Attributes 但没有记录 Class 的 Dataset
2. Training Dataset: 已知记录的 Attributes 以及 Class
3. 计算距离的方法（一般使用 Euclidean distance）
   

使用 Nearest neighbor algorithm的操作步骤：

1. 计算Test Dataset中的一条数据与所有Training Set之间的distance

   • 计算Distance中需要进行Normalization

     $$x^{\prime }=\frac{x?min(x)}{max(x)?min(x)}$$
     eg:
     

   • Calculating distance for nominal attributes(计算非数字的attributes之间的距离)

     • 需要根据任务和数据类型的类型有多种选择； 需要领域专业知识

       eg：

       • difference = 0 if attribute values are the same
       • difference = 1 if they are not

   • Weighted nearest neighbor

     • 目的：预测时，让近邻比远亲占比重更大，从而优 化预测结果

     • 步骤：按照距离来衡量每个样本在最后vote的时候 所占权重
       $$weight=\frac{1}{d^2}$$

     • 实现：在选出K个最近邻后，将他们按如上公式分 别计算权重，并加到对应的类别上，最后比对类别 所占总的权重大小，而不是看票数

     • 问题：对noise更敏感

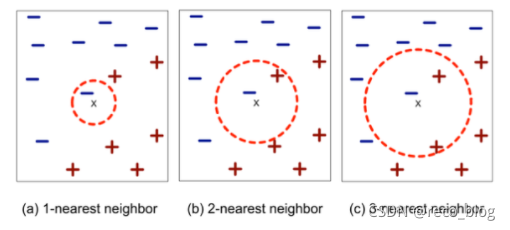
2. 定义K的值

   1. 如果最近邻类别1:1怎么办?
      K取奇数
   2. K值取得太小会怎么样?
      影响模型的鲁棒性( Robust )，对噪音点敏感
   3. K值取得太大会怎么样?
      最近邻可能包含其他类的成员

3. 使用K条Nearest neighbor来定义Test set中数据的类别

   • 距离最接近k条数据的class定义为此条数据的class

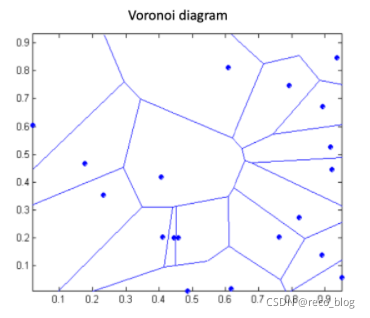
Decision boundary of 1-nearest neighbor

1. 每个数据点都拥有一块Voronoi region，在这之 中的数据点都是离它最近的，故可以当做1- nearest neighbor的决策边界

2. 每根线都是某两个数据点的垂直平分线的一截

   

K-nearest neighbor - 讨论

1. 通常十分准确

2. 对K的值非常敏感

3. 需要Nomolization：KNN算法依靠距离来实现分类，所以某些特征的值过大会极大地影响算法 准确率，可能不得不进行归一化以防止距离度量被某些特征所控制

4. Lasy learner：

   • 没有建立模型
   • 预测的时间成本很高，尤其是数据量很大的时候，所以需要使用高效的数据结构eg. KD tree

5. 对于高维数组不友好

   • 时间成本太高
   • 需要降纬处理

6. 可以生成由 Voronoi 边的子集定义的任意形状的决策边界