1.前言
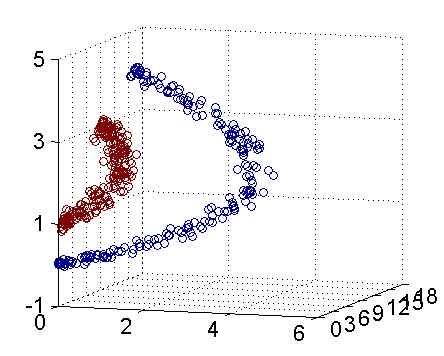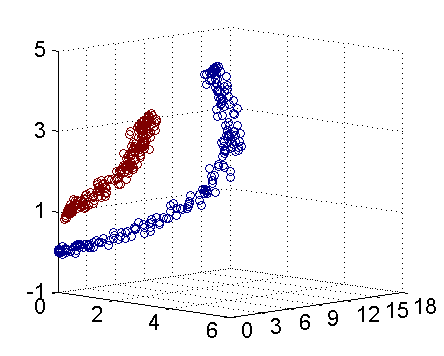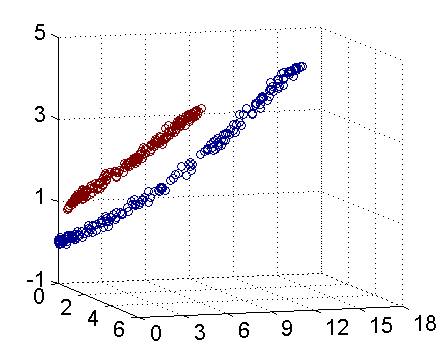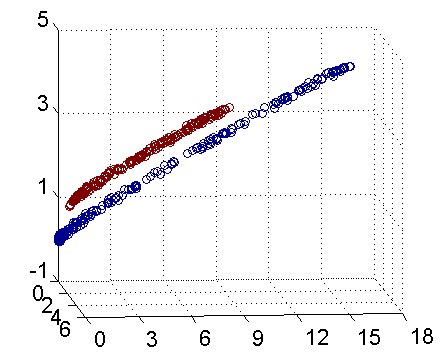
??在前两篇文章中,我们主要讨论了数据线性可分和数据近似线性可分的情况,但是有些时候数据可能是非线性可分的,此时前两种模型将不再适用。如图1所示,显然在二维空间中无法找到一条直线将正负实例点分开,但是将数据从二维升为三维之后,便可找到一个分离超平面将正负实例点完全分开了,这就是非线性支持向量机的基本思路。即先使用一个变换将输入空间的数据映射到特征空间中,然后在特征空间中使用线性分类学习方法从训练数据中学习分类模型。我的理解是,将非线性可分的数据变换到特征空间后,特征空间中的数据变成了线性可分或者近似线性可分的,这时再在特征空间中学习线性支持向量机,从而实现非线性可分数据的分类。

2.核函数
??核函数的定义:设
χ
\chi
χ是输入空间,
H
H
H为特征空间,如果存在一个从
χ
\chi
χ到
H
H
H的映射:
χ
→
H
\chi \to H
χ→H使得对所有
x
,
z
∈
χ
\boldsymbol{x},\boldsymbol{z} \in \chi
x,z∈χ,满足条件:
K
(
x
,
z
)
=
?
(
x
)
?
?
(
z
)
K(\boldsymbol{x},\boldsymbol{z})=\phi(\boldsymbol{x}) \cdot \phi(\boldsymbol{z})
K(x,z)=?(x)??(z),则称
K
(
x
,
z
)
K(\boldsymbol{x},\boldsymbol{z})
K(x,z)为核函数,
?
(
x
)
\phi(\boldsymbol{x})
?(x)为映射函数,其中
?
(
x
)
?
?
(
z
)
\phi(\boldsymbol{x}) \cdot \phi(\boldsymbol{z})
?(x)??(z)为
?
(
x
)
\phi(\boldsymbol{x})
?(x)和
?
(
z
)
\phi(\boldsymbol{z})
?(z)的内积。
??直观上的理解就是通过核函数这个工具来将数据从输入空间映射到特征空间的,但是为什么不直接使用映射函数
?
(
x
)
\phi(\boldsymbol{x})
?(x)而是使用核函数呢?首先,直接计算核函数
K
(
x
,
z
)
K(\boldsymbol{x},\boldsymbol{z})
K(x,z)比较容易,而通过
?
(
x
)
?
?
(
z
)
\phi(\boldsymbol{x}) \cdot \phi(\boldsymbol{z})
?(x)??(z)计算核函数相对困难;其次,我们观察在前一篇文章中所推出的线性支持向量机对偶问题的目标函数:
α
m
i
n
?
1
2
∑
i
=
1
N
∑
j
=
1
N
α
i
α
j
y
i
y
j
(
x
i
?
x
j
)
?
∑
i
=
1
N
α
i
{_\boldsymbol{\alpha}^{min}}\ \frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_i \alpha_j y_i y_j(\boldsymbol{x}_i \cdot \boldsymbol{x}_j)-\sum_{i=1}^{N}\alpha_i
αmin??21?i=1∑N?j=1∑N?αi?αj?yi?yj?(xi??xj?)?i=1∑N?αi?以及分离超平面的表达式:
∑
i
=
1
N
α
i
?
y
i
(
x
i
?
x
)
+
b
?
=
0
\sum_{i=1}^{N}\alpha^*_i y_i (\boldsymbol{x}_i \cdot \boldsymbol{x})+b^*=0
i=1∑N?αi??yi?(xi??x)+b?=0可以发现:其中只涉及到输入实例与实例之间的内积,所以将数据从输入空间变换到特征空间后,我们依然只需要知道
?
(
x
)
?
?
(
z
)
\phi(\boldsymbol{x}) \cdot \phi(\boldsymbol{z})
?(x)??(z),而不需要单独计算出
?
(
x
)
\phi(\boldsymbol{x})
?(x)的值和
?
(
z
)
\phi(\boldsymbol{z})
?(z)的值,这也是为什么直接用核函数的原因之一。
??在实际的任务中,最常用的核函数为高斯核函数,其表达式如下:
K
(
x
,
z
)
=
exp
(
?
∣
∣
x
?
z
∣
∣
2
2
σ
2
)
K(\boldsymbol{x},\boldsymbol{z})=\text{exp}(-\frac{||\boldsymbol{x}-\boldsymbol{z}||^2}{2\sigma^2})
K(x,z)=exp(?2σ2∣∣x?z∣∣2?)
3.非线性支持向量机
??将线性支持向量机对偶问题中的
x
j
?
x
j
\boldsymbol{x}_j \cdot \boldsymbol{x}_j
xj??xj?替换为核函数
K
(
x
i
,
x
j
)
K(\boldsymbol{x}_i,\boldsymbol{x}_j)
K(xi?,xj?)就得到了非线性支持向量机的最优化问题表达式:
α
m
i
n
?
1
2
∑
i
=
1
N
∑
j
=
1
N
α
i
α
j
y
i
y
j
K
(
x
i
,
x
j
)
?
∑
i
=
1
N
α
i
s
.
t
.
?
∑
i
=
1
N
α
i
y
i
=
0
0
≤
α
i
≤
C
{_\boldsymbol{\alpha}^{min}}\ \frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_i \alpha_j y_i y_jK(\boldsymbol{x}_i,\boldsymbol{x}_j)-\sum_{i=1}^{N}\alpha_i \\ s.t.\ \sum_{i=1}^{N}\alpha_i y_i =0 \\ 0 \le \alpha_i \le C
αmin??21?i=1∑N?j=1∑N?αi?αj?yi?yj?K(xi?,xj?)?i=1∑N?αi?s.t.?i=1∑N?αi?yi?=00≤αi?≤C??对于给定的训练数据集
T
=
{
(
x
1
,
y
1
)
,
(
x
2
,
y
2
)
,
.
.
.
,
(
x
N
,
y
N
)
}
T=\{(\boldsymbol{x_1},y_1),(\boldsymbol{x_2},y_2),...,(\boldsymbol{x_N},y_N)\}
T={(x1?,y1?),(x2?,y2?),...,(xN?,yN?)},其中
x
1
∈
χ
=
R
n
\boldsymbol{x_1}\in \chi = R^n
x1?∈χ=Rn,
y
i
∈
{
+
1
,
?
1
}
y_i \in \{+1,-1\}
yi?∈{+1,?1},
i
=
1
,
2
,
3
,
.
.
.
.
,
N
i=1,2,3,....,N
i=1,2,3,....,N,非线性支持向量机的求解过程与线性支持向量机相差不多,过程如下:
(1)选取适当的核函数
K
(
x
,
z
)
K(\boldsymbol{x},\boldsymbol{z})
K(x,z)和适当的惩罚因子
C
C
C,构造并求解上面给出的最优化问题,求得最优解
α
?
=
(
α
1
?
,
α
2
?
,
.
.
.
,
α
N
?
)
T
\boldsymbol{\alpha}^*=({\alpha}^*_1,{\alpha}^*_2,...,{\alpha}^*_N)^T
α?=(α1??,α2??,...,αN??)T;
(2)选择
α
?
\boldsymbol{\alpha^*}
α?的一个正分量
0
<
α
j
?
<
C
0 < \alpha^*_j < C
0<αj??<C,根据公式求得
b
?
b^*
b?:
b
?
=
y
j
?
∑
i
=
1
N
α
i
?
y
i
K
(
x
i
?
x
j
)
b^*=y_j-\sum_{i=1}^{N}\alpha^*_i y_iK(\boldsymbol{x}_i \cdot \boldsymbol{x}_j)
b?=yj??i=1∑N?αi??yi?K(xi??xj?)(3)构造决策函数:
f
(
x
)
=
sign
(
∑
i
=
1
N
α
i
?
y
i
K
(
x
i
?
x
)
+
b
?
)
f(\boldsymbol{x})=\text{sign}(\sum_{i=1}^{N}\alpha^*_i y_i K(\boldsymbol{x}_i \cdot \boldsymbol{x})+b^*)
f(x)=sign(i=1∑N?αi??yi?K(xi??x)+b?)当核函数为高斯核函数时,对应的支持向量机是高斯径向基函数分类器,分类决策函数则为:
f
(
x
)
=
sign
(
∑
i
=
1
N
α
i
?
y
i
exp
(
?
∣
∣
x
?
z
∣
∣
2
2
σ
2
)
+
b
?
)
f(\boldsymbol{x})=\text{sign}(\sum_{i=1}^{N}\alpha^*_i y_i \text{exp}(-\frac{||\boldsymbol{x}-\boldsymbol{z}||^2}{2\sigma^2})+b^*)
f(x)=sign(i=1∑N?αi??yi?exp(?2σ2∣∣x?z∣∣2?)+b?)
4.参考资料
1.李航《统计学习方法》
2.https://blog.csdn.net/u010199356/article/details/88836026
