[人工智能]【机器学习实战】Ch 4: 训练模型

线性回归

# an example
import numpy as np
import matplotlib.pyplot as plt

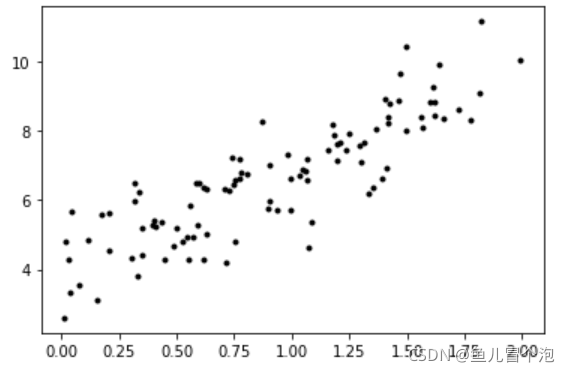
X = 2 * np.random.rand(100, 1)
y = 3 * X + 4 + np.random.randn(100, 1)

plt.plot(X, y, 'k.')
plt.show()

X_b = np.c_[np.ones((100, 1)), X]
theta = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y)

theta
# array([[3.91711324],
#        [2.934259  ]])

使用sklearn进行线性回归：

from sklearn.linear_model import LinearRegression

lin_reg = LinearRegression()
lin_reg. fit(X, y)

lin_reg.intercept_, lin_reg.coef_
# (array([3.91711324]), array([[2.934259]]))
# Scikit-Learn 将偏差项（intercept_）核特征权重（coef_）分开

梯度下降

1、批量梯度下降
计算梯度下降的每一步时，都是基于完整的训练集X

eta = 0.1
n_iterations = 1000
m = 100

theta = np.random.randn(2, 1)

for iteration in range(n_iterations):
    gradients = 2/m * X_b.T.dot(X_b.dot(theta) - y)
    theta = theta - eta * gradients

theta
# array([[3.91711324],
#       [2.934259  ]])

2、随机梯度下降
每一步在训练集中随机选择一个实例，并基于该单个实例计算梯度

当成本函数非常不规则时， 随机梯度下降可以帮助算法跳出局部最小值。相比批量梯度下降，随机梯度下降对寻找全局最小值更有优势。

随机性的好处在于可以逃离局部最优，但是缺点是永远定位不出最小值
解决方法：逐渐降低学习率——模拟退火

n_epochs = 50
t0, t1 = 5, 50    # learning schedule hyperparameters

def learning_schedule(t):
    return t0/(t + t1)

theta = np.random.randn(2, 1)

for epoch in range(n_epochs):
    for i in range(m):
        random_index = np.random.randint(m)
        xi = X_b[random_index:random_index + 1]
        yi = y[random_index:random_index + 1]
        gradients = 2 * xi.T.dot(xi.dot(theta) - yi)
        eta = learning_schedule(epoch * m + i)
        theta = theta - eta * gradients

theta
# array([[3.97165339],
#       [2.94092433]])

使用随机梯度下降时， 训练实例必须保持独立且均匀分布（IID），以确保平均而言将参数拉向全局最优值。确保这一点的一个简单方法时在训练过程中对实例进行随机混洗

使用带有Scikit-Learn的随机梯度下降执行线性回归

from sklearn.linear_model import SGDRegressor

# run until iterations == 1000 or loss < 0.001 (max_iter=1000, tol = 1e-3)
# learning rate = 0.1 (eta0=0.1)
# No ragularization (penalty=None)
sgd_reg = SGDRegressor(max_iter=1000, tol=1e-3, penalty=None, eta0=0.1)
sgd_reg.fit(X, y.ravel())
# rival() ： Flatten multidimensional array

sgd_reg.intercept_, sgd_reg.coef_
# (array([4.37064466]), array([2.85664733]))

3、小批量梯度下降
每一步中，不是根据完整的训练集（如批量梯度下降）或仅基于一个实例（如随机梯度下降）来计算梯度

多项式回归

多项式回归：可以用线性模型拟合非线性模型。 将每个特征的幂次方添加为一个新特征， 然后在此拓展训练集上训练一个线性模型

# an example
import numpy as np
import matplotlib.pyplot as plt

m = 100
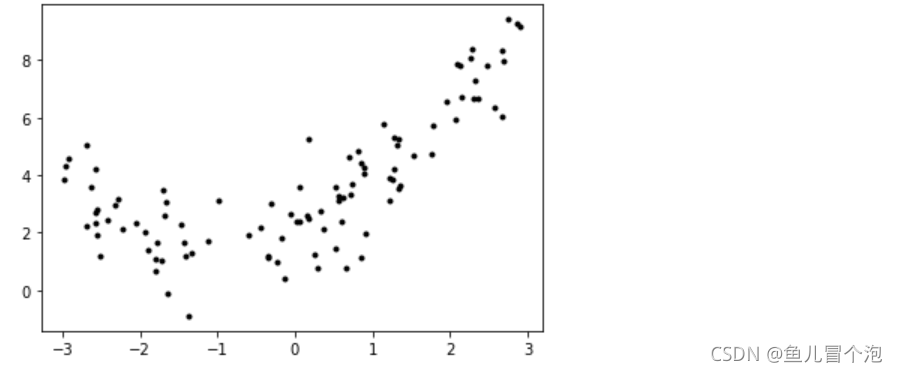
X = 6 * np.random.rand(m, 1) - 3
y = 0.5 * X**2 + X + 2 + np.random.randn(m, 1)

plt.plot(X, y, 'k.')
plt.show()

from sklearn.preprocessing import PolynomialFeatures

poly_features = PolynomialFeatures(degree=2, include_bias=False)
X_poly = poly_features.fit_transform(X)

X[0], X_poly[0]
# (array([-2.57177719]), array([-2.57177719,  6.61403794]))

from sklearn.linear_model import LinearRegression

lin_reg = LinearRegression()
lin_reg.fit(X_poly, y)

lin_reg.intercept_, lin_reg.coef_
# (array([2.13509276]), array([[1.00195518, 0.50394306]]))
# 模型估算： y = 0.503 * x^2 + 1.002 * x + 2.135