[人工智能]李宏毅机器学习--P6梯度下降法

• Review: gradient Descent
• Learning rates给优化过程中带来的影响
• 自适应调整learning rate 的方法
• 梯度下降法的背后理论基础

Review: gradient Descent
在上一个视频里，已经介绍了使用梯度下降法求解Loss function
$${\theta }^{?}=argminL(\theta )$$
L:loss function $\theta$:参数

梯度下降过程中的可视化

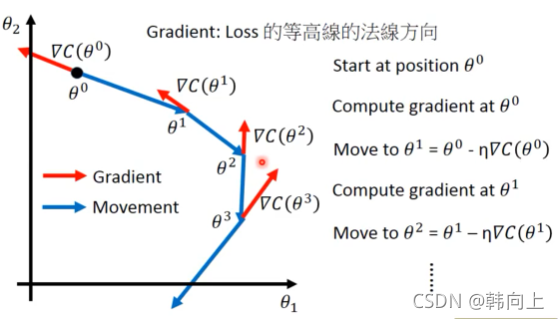
Learning rates给优化过程中带来的影响

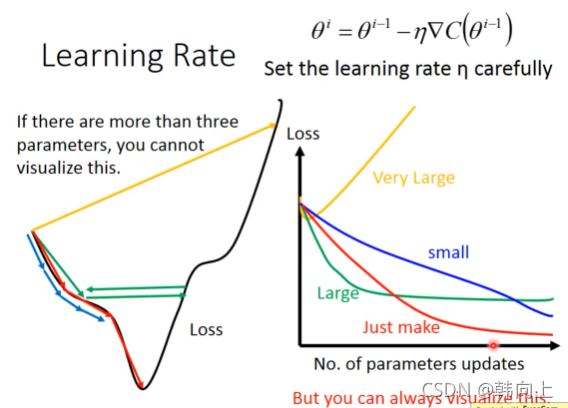
自适应调整learning rate 的方法

1. Adagrad
   以权重$w$的更新过程为例
   $$w^{t+1}\leftarrow w^t?\frac{{\eta }^t}{{\sigma }^t}{g}^t$$
   其中${\eta }^t=\frac{\eta }{\sqrt{t+1}}$, ${\sigma }^t=\sqrt{\frac{1}{t+1}{\sum }_{i=0}^t(g_i^t{)}^2}$.
   
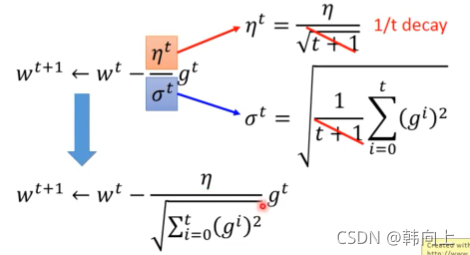
   如何理解Adagrad的物理意义呢？
   如下图所示，当只有一个参数时，微分越大说明当前参数距离最优参数越远
   
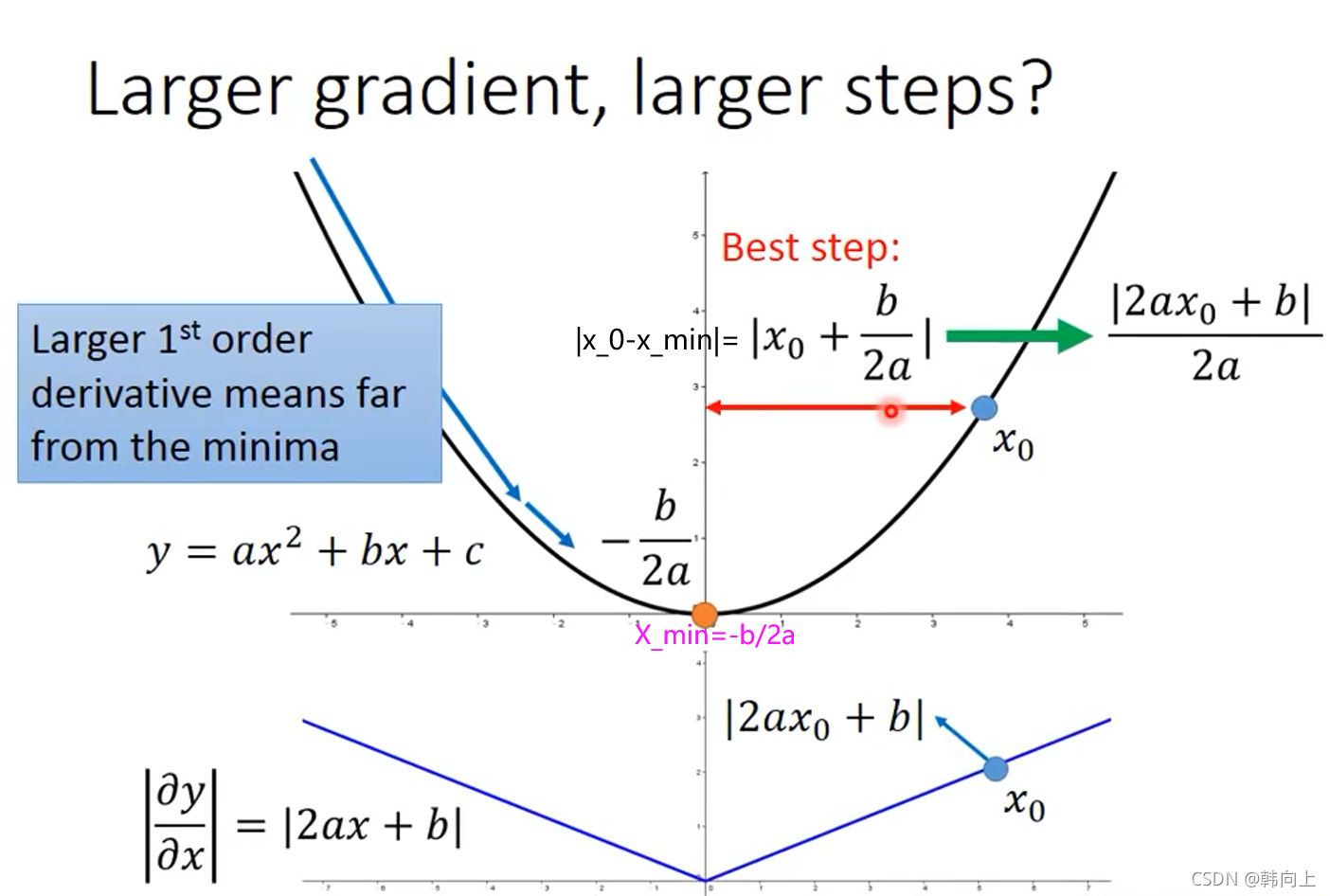
   当时当需要同时考虑多个参数时，考虑微分越大当前参数距离最优参数越远是一种不正确的想法，可见绿色的线中$c$点相比于蓝色的线中$a$点的微分值大，但$c$距离最优解比$a$近。
   
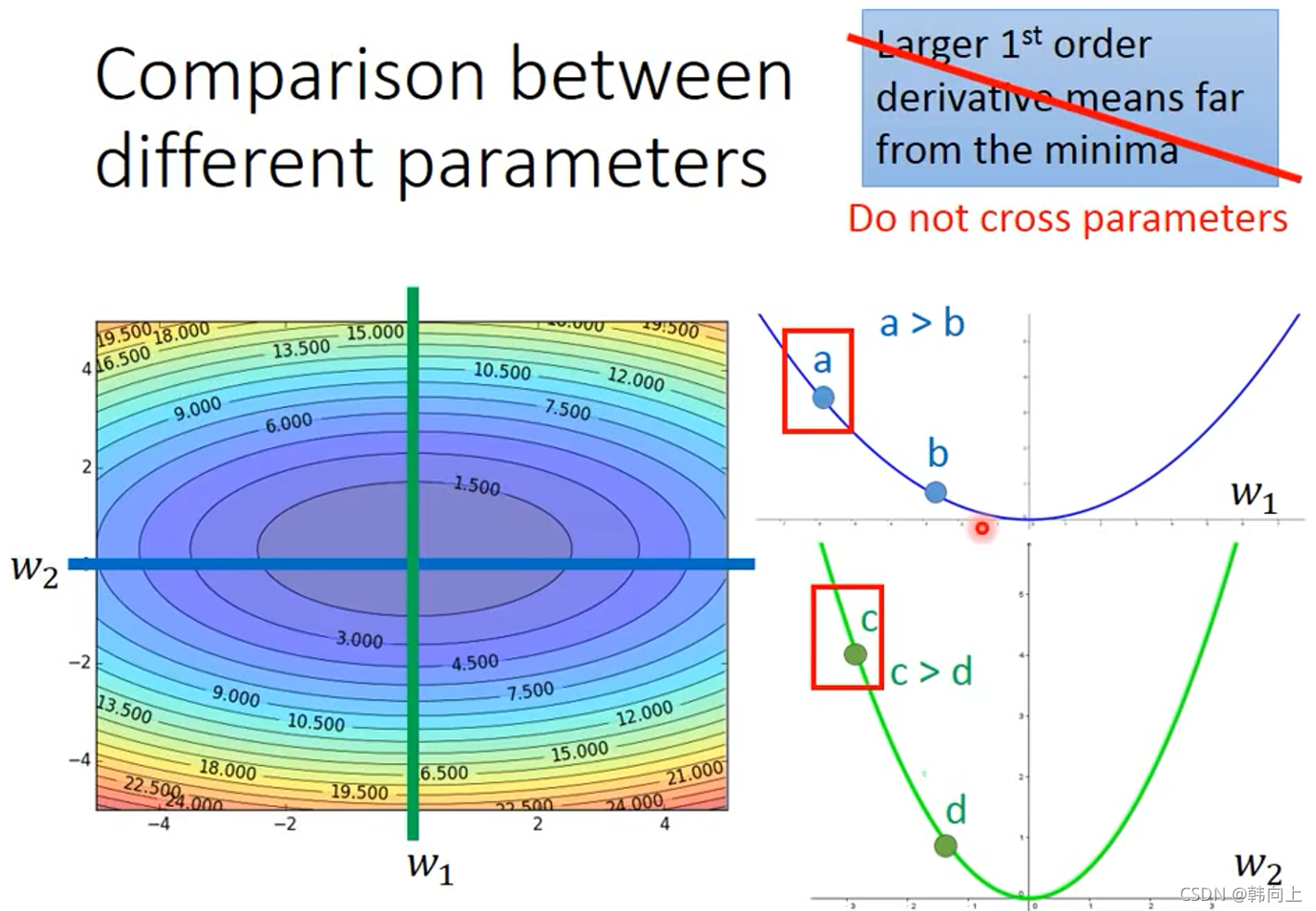
   那么为了同时考虑好几个参数时，我们应该将描述一阶微分变化的二次微分也需要考虑进来. $\frac{fristderivative}{secondderivative}$
   
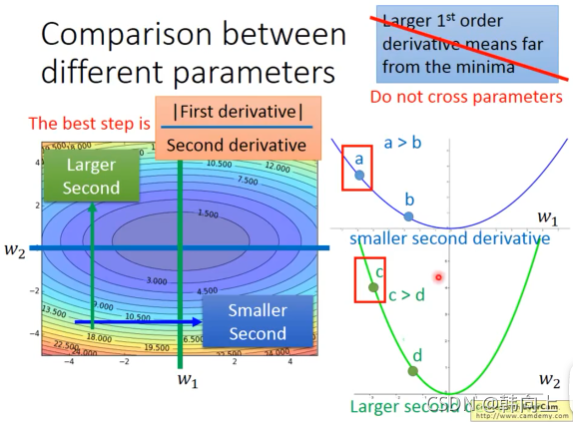
   在Adagrad中，${\sigma }^t=\sqrt{\frac{1}{t+1}{\sum }_{i=0}^t(g_i^t{)}^2}$, 具有体现反差的效果。
   
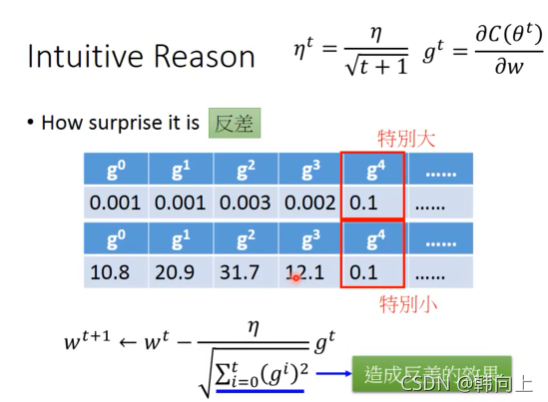
   我认为Adagrad具有这样的作用：损失函数在最优解处的微分值为0，在最优解附近的邻域内其他点处微分也应该较缓。Adagrad让一直陡峭突然变缓时，让函数快点走走，避免陷入局部最优解。一直平缓突然陡峭时让函数变慢点，别跨越最优解了。
2. Stochastic Gradient Descent
   
   
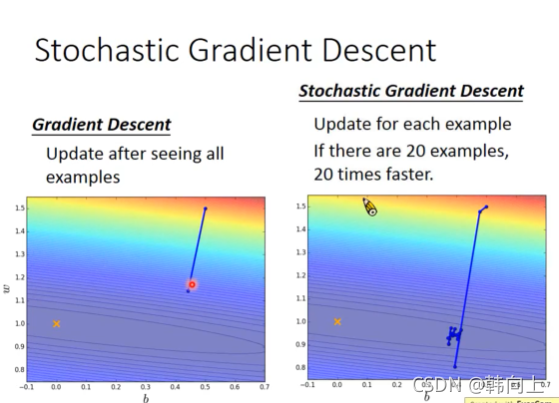
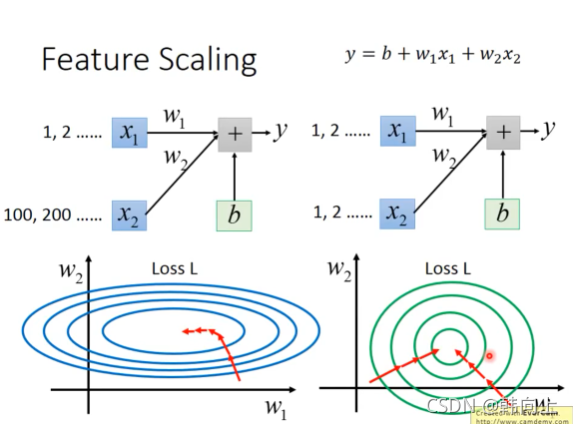
3. Feature Scaling
   归一化不同数据的分布，可以看出没有归一化是找最优解是需要拐弯才能到，但是绿色线直走就能到。
   
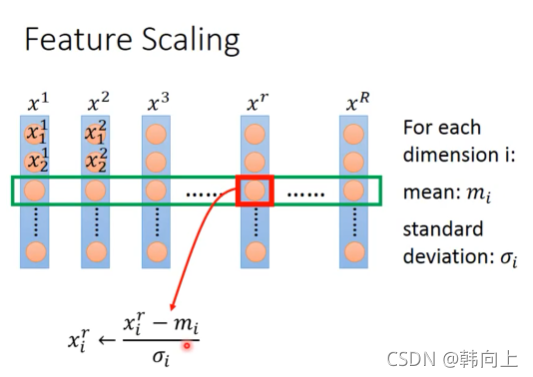
   归一化的方法：
   
   梯度下降法的背后理论基础
   假设在损失函数中，我们需要更新两个参数${\theta }_1,{\theta }_2$.
   对于一个二阶可微函数$L({\theta }_1,{\theta }_2)$，在$(a,b)$附近的一个邻域内，$L({\theta }_1,{\theta }_2)$可以被表述如下
   $$L({\theta }_1,{\theta }_2)\approx =s+u({\theta }_1?a)+v({\theta }_2?b)$$
   其中$s=L(a,b)$, $u=\frac{?L(a,b)}{?{\theta }_1}$, $v=\frac{?L(a,b)}{?{\theta }_2}$。
   

那么为了使得整体的L最小，我们就需要
把向量$(({\theta }_1?a),({\theta }_2?b))$置于与$(u,v)$相反。


红色圈的半径就是学习率$\eta$。当红色圈过大时，$L({\theta }_1,{\theta }_2)\approx =s+u({\theta }_1?a)+v({\theta }_2?b)$就会误差过大。

图源：李宏毅机器学