基于分析Laplace方程“放射状”函数特解的基本解引入
参考文献:【偏微分方程笔记(2)——Laplace(位势)方程的基本解】
1. 基本定义
关于函数
u
(
x
1
,
x
2
,
.
.
.
,
x
n
)
u(x_1,x_2,...,x_n)
u(x1?,x2?,...,xn?)的
n
n
n维Laplace方程是:
Δ
u
=
u
x
1
x
1
+
u
x
2
x
2
+
.
.
.
+
u
x
n
x
n
=
0
(1)
\Delta u=u_{x_1x_1}+u_{x_2x_2}+...+u_{x_nx_n}=0 \tag 1
Δu=ux1?x1??+ux2?x2??+...+uxn?xn??=0(1)
它的解称为调和函数或势函数。
2. 寻找特解
由于Laplace方程作旋转以后是不变的,因此我们似乎可以先去找“放射状(radial)”的函数,也就是:
r
=
∣
x
∣
=
x
1
2
+
.
.
.
+
x
n
2
(2)
r=|x|=\sqrt{x_1^2+...+x_n^2} \tag 2
r=∣x∣=x12?+...+xn2??(2)
首先尝试在
n
n
n维线性空间中寻找满足Laplace方程
(
1
)
(1)
(1)的一个解
u
u
u,具有形式:
u
(
x
)
=
v
(
r
)
(3)
u(x)=v(r) \tag 3
u(x)=v(r)(3)
首先注意到对于
i
=
1
,
2
,
.
.
.
,
n
i=1,2,...,n
i=1,2,...,n,有:
?
r
?
x
i
=
1
2
x
1
2
+
.
.
.
+
x
n
2
2
x
i
=
x
i
r
(
x
=?
0
)
(4)
\frac{\partial r}{\partial x_i} = \frac{1}{2\sqrt{x_1^2+...+x_n^2}} 2x_i = \frac{x_i}{r}(x \not =0) \tag 4
?xi??r?=2x12?+...+xn2??1?2xi?=rxi??(x?=0)(4)
因此:
u
(
x
)
u(x)
u(x)的一阶导数有:
u
x
i
=
?
v
?
r
?
r
?
x
i
=
v
′
(
r
)
x
i
r
(5)
u_{x_i}=\frac{\partial v}{\partial r} \frac{\partial r}{\partial x_i} = v'(r) \frac{x_i}{r} \tag 5
uxi??=?r?v??xi??r?=v′(r)rxi??(5)
u
(
x
)
u(x)
u(x)的二阶导数有:
u
x
i
x
i
=
?
u
x
i
?
x
i
=
?
?
x
i
(
?
v
?
r
?
r
?
x
i
)
=
?
2
v
?
x
i
?
r
?
r
?
x
i
+
?
2
r
?
x
i
?
x
i
?
v
?
r
=
[
?
?
r
?
r
?
x
i
(
v
′
(
r
)
)
]
?
x
i
r
+
[
?
?
x
i
(
x
i
r
)
]
?
v
′
(
r
)
(6)
u_{x_ix_i}=\frac{\partial u_{x_i}}{\partial x_i}=\frac{\partial}{\partial x_i} (\frac{\partial v}{\partial r} \frac{\partial r}{\partial x_i}) \\ = \frac{\partial^2 v}{\partial x_i \partial r} \frac{\partial r}{\partial x_i} + \frac{\partial^2 r}{\partial x_i \partial x_i} \frac{\partial v}{\partial r} \\ =[\frac{\partial}{\partial r} \frac{\partial r}{\partial x_i}(v'(r))]·\frac{x_i}{r} + [\frac{\partial}{\partial x_i} (\frac{x_i}{r})]·v'(r) \tag 6
uxi?xi??=?xi??uxi???=?xi???(?r?v??xi??r?)=?xi??r?2v??xi??r?+?xi??xi??2r??r?v?=[?r???xi??r?(v′(r))]?rxi??+[?xi???(rxi??)]?v′(r)(6)
对于前式中括号中的式子:
?
?
r
(
x
i
v
′
(
r
)
r
)
=
x
i
[
v
′
′
(
r
)
r
?
v
′
(
r
)
]
r
2
(7)
\frac{\partial}{\partial r} (\frac{x_i v'(r)}{r}) = \frac{x_i[v^{''}(r)r-v'(r)]}{r^2} \tag 7
?r??(rxi?v′(r)?)=r2xi?[v′′(r)r?v′(r)]?(7)
对于后式中括号中的式子:
?
?
x
i
(
x
i
r
)
=
1
r
(8)
\frac{\partial}{\partial x_i} (\frac{x_i}{r}) = \frac{1}{r} \tag 8
?xi???(rxi??)=r1?(8)
故
u
(
x
)
u(x)
u(x)的二阶偏导数:
u
x
i
x
i
=
v
′
′
(
r
)
x
i
2
r
2
+
v
′
(
r
)
(
1
r
?
x
i
2
r
3
)
(9)
u_{x_ix_i}=v^{''}(r) \frac{x_i^2}{r^2} + v'(r) (\frac{1}{r}-\frac{x_i^2}{r^3}) \tag 9
uxi?xi??=v′′(r)r2xi2??+v′(r)(r1??r3xi2??)(9)
因此:
Δ
u
=
v
′
′
(
r
)
+
n
?
1
r
v
′
(
r
)
(10)
\Delta u=v^{''}(r)+\frac{n-1}{r} v'(r) \tag {10}
Δu=v′′(r)+rn?1?v′(r)(10)
因此
Δ
u
=
0
\Delta u=0
Δu=0当且仅当
v
′
′
+
n
?
1
r
v
′
=
0
(11)
v^{''}+\frac{n-1}{r} v'=0 \tag {11}
v′′+rn?1?v′=0(11)
3. 解常微分方程
如果
v
′
=?
0
v' \not =0
v′?=0,则:
l
n
(
∣
v
′
∣
)
′
=
v
′
′
v
′
=
1
?
n
r
(12)
ln(|v'|)'=\frac{v^{''}}{v'}=\frac{1-n}{r} \tag {12}
ln(∣v′∣)′=v′v′′?=r1?n?(12)
存在常数
a
a
a使得:
v
′
(
r
)
=
a
r
n
?
1
(13)
v'(r)=\frac{a}{r^{n-1}} \tag {13}
v′(r)=rn?1a?(13)
因此如果
r
>
0
r>0
r>0,我们有:
当
n
=
1
n=1
n=1时:
v
(
r
)
=
a
r
(14)
v(r)=ar \tag {14}
v(r)=ar(14)
当
n
=
2
n=2
n=2时:
v
(
r
)
=
b
?
l
n
r
+
c
(15)
v(r)=b \ ln r+c \tag {15}
v(r)=b?lnr+c(15)
当
n
≥
3
n \geq 3
n≥3时:
v
(
r
)
=
b
r
n
?
2
+
c
(16)
v(r)=\frac{b}{r^{n-2}}+c \tag {16}
v(r)=rn?2b?+c(16)
这里
b
,
c
b,c
b,c均为常数。
4. 基本解
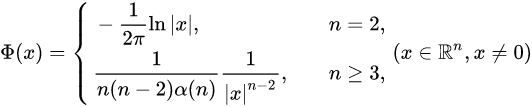
该方程组称为Laplace方程的基本解,这里
α
(
n
)
=
R
n
\alpha(n)=R^n
α(n)=Rn中单位球的体积=
π
n
τ
(
n
2
+
1
)
\frac{\sqrt{\pi^n}}{\tau (\frac{n}{2}+1)}
τ(2n?+1)πn??。