BPE(Byte Pair Encoding)分词

BPE是一种根据字节对进行编码的算法。主要目的是为了数据压缩，算法描述为字符串里频率最常见的一对字符被一个没有在这个字符中出现的字符代替的层层迭代过程。基本思路是将使用最频繁的字节用一个新的字节组合代替，比如用字符的n-gram替换各个字符。例如，假设(‘A’, ‘B’) 经常顺序出现，则用一个新的标志’AB’来代替它们。

Transformer NLP 预训练模型都通过 embedding 词典来表征词义，当遇见没见过的词的时候，以前是用""代替，这样会造成对新事物(新词、网络词、简写词)理解能力很差，BPE就是来解决这个问题的。英文中会有词根和造词现象例如: “greenhand” 如果你的词典中没有这个词，那么就可以把它拆成“green”,“hand”两个词，这里green 向量会跟发芽一类的词相近有新生的意思，hand有操作、手的意思那么就不难推测出greenhand是新手。这个过程中会参考一个词典，这个词典从上往下是一个个词对，对应的顺序就是它出现的频率，越往上的词越高频率。对应中文相当于分词了。

2016年，Sennrich提出采用分词算法（word segmentation）构建BPE，并将其应用于机器翻译任务中。论文提出的基本思想是，给定语料库，初始词汇库仅包含所有的单个字符。然后，模型不断地将出现频率最高的n-gram pair作为新的n-gram加入到词汇库中，直到词汇库的大小达到我们所设定的某个目标为止。该算法在论文：https://arxiv.org/abs/1508.07909 Neural Machine Translation of Rare Words with Subword Units详细介绍

训练过程：

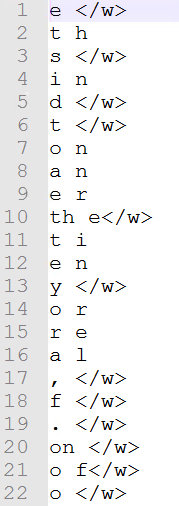
对于使用子词作为基本单位进行训练的神经机器翻译模型，训练的第一步就是根据语料生成bpe的code资源，以英文为例，该资源会将训练语料以字符为单位进行拆分，按照字符对进行组合，并对所有组合的结果根据出现的频率进行排序，出现频次越高的排名越靠前，排在第一位的是出现频率最高的子词。如图所示：e 为出现频率最高的子词，其中表示这个e是作为单词结尾的字符。训练过程结束，会生成codec文件。如下图所示：

解码过程

以单词“where”为例，首先按照字符拆分开，然后查找codec文件，逐对合并，优先合并频率靠前的字符对。85 319 9 15 表示在该字符对在codec文件中的评率排名。

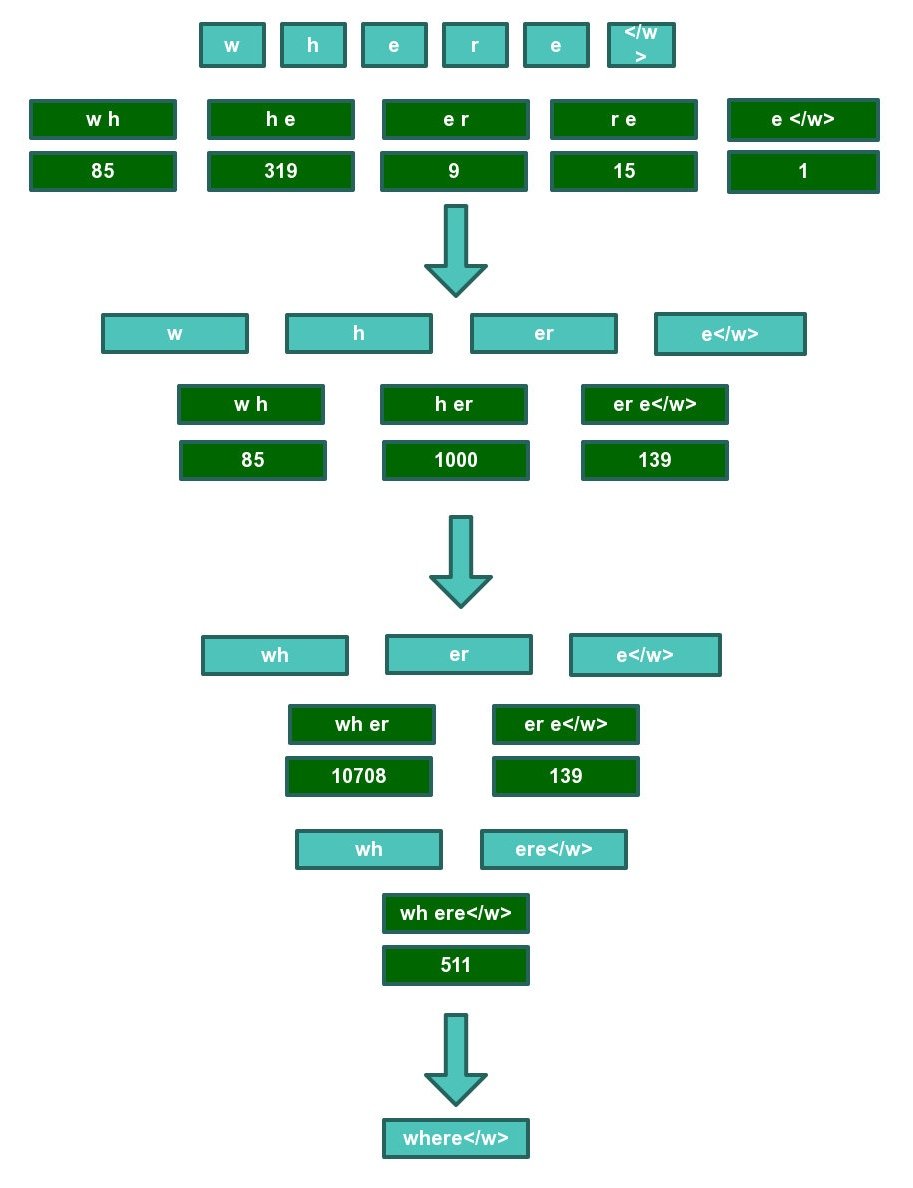
最终where可以在codec文件中被找到，因此where的bpe分词结果为where，对于其他并不能像where一样能在codec文件中找到整个词的词来说，bpe分词结果以最终查询结束时的分词结果为准。

sentencepiece工具包

sentencepiece是一个google开源的自然语言处理工具包，支持bpe、unigram等多种分词方法。其优势在于：bpe、unigram等方法均假设输入文本是已经切分好的，只有这样bpe才能统计词频（通常直接通过空格切分）。但问题是，汉语、日语等语言的字与字之间并没有空格分隔。sentencepiece提出，可以将所有字符编码成Unicode码（包括空格），通过训练直接将原始文本（未切分）变为分词后的文本，从而避免了跨语言的问题。

实验表明，当英文的词表大小设定为32000时，可以覆盖数据集中词频为10以上的bpe组合；中文词表大小设定为32000时，覆盖了数据集中词频为21以上的bpe组合。进一步扩大词表，会导致词表过大，含有的非常用词增多，模型的训练参数也会增多。因此，我们设定中英文词表大小均为32000。根据sentencepiece代码说明，character_coverage这一参数在字符集较大的中文分词中设置为0.995，在字符集较小的英文分词中设置为1。

LabelSmoothing

Label Smoothing 是一种正则化的方法，对标签平滑化处理以防止过拟合。

对于分类问题，特别是多分类问题，常常把向量转换成one-hot-vector（独热向量），选择概率最大的作为我们的预测标签。然而在实际过程中，对于损失函数，我们需要用预测概率去拟合真实概率，而拟合one-hot的真实概率函数会带来两个问题：

无法保证模型的泛化能力，容易造成过拟合；
全概率和0概率鼓励所属类别和其他类别之间的差距尽可能加大，而由梯度有界可知，这种情况很难适应。会造成模型过于相信预测的类别

交叉熵损失函数的实际是在最小化预测概率与真实标签概率的交叉熵：
$L=-\sum_iy_ilogp_i$
如果分类准确，交叉熵损失函数的结果是0（即上式中p和y一致的情况），否则交叉熵为无穷大。也就是说交叉熵对分类正确给的是最大激励。换句话说，对于标注数据来说，这个时候我们认为其标注结果是准确的(对于真实标签概率的取值要么是1，要么是0，表征我们已知样本属于某一类别的概率是为1的确定事件,属于其他类别的概率则均为0)。但是，对于一个由多人标注的数据集，不同人标注的准则可能不同，每个人的标注也可能会有一些错误。模型对标签的过分信任，可能会造成过拟合。那么这时候，使用交叉熵损失函数作为目标函数并不一定是最优的。

label smoothing的原理就是为损失函数增强其他标签的损失函数值。类似于其为非标签的标签增加了一定概率的可选择性。假设标签光滑化处理标签真实概率的表达式为：
$(1-\epsilon) y + \frac {\epsilon}{K}$
原理：对于以Dirac函数分布的真实标签，我们将它变成分为两部分获得（替换）。

第一部分：将原本Dirac分布的标签变量替换为(1 - ?)的Dirac函数；
第二部分：以概率 ? ，将其替换为在u(k) 分布中的随机变量（u（k）是类别分之一即 $\frac {1}{K}$ ）

当 $y$ 为真实标签的时候，概率取值为 $(1-\epsilon) + \frac {\epsilon}{K}$ ，否则取概率 $\frac {\epsilon}{K}$ 。

如：假设存在标签[0, 1, 2]

取 $\epsilon=0.1$ ，当某个样本真实标签为 $y = 0$ 的时候，损失函数值计算如下：
$L=-0.93logp_0 - 0.03 logp_1 - 0.03 logp_2$
其中 $p_0, p_1, p_1$ 表示该模型将该标签分别预测为这三个标签的概率， $p_0+p_1+p_1=1$

不进行标签光滑化处理的话，该样本损失函数值计算如下：
$L=-logp_0$