[人工智能]（三）描述性统计分析与绘图

1 描述性统计分析

1.1 概念

1. 数据变量度量类型

名义： 字符（原义）、数值（编码）
等级 ：字符、数值 有排序 ‘小中大’ 差值无意义
连续 ：数值 ‘age’
#连续变量分组，当成等级变量使用，可使数据更稳健
#名义变量和等级变量统称为分类变量。
统计量：频次、百分比

2. 描述名义变量的分布

频次、百分比
#python所用包都不支持字符，需要编码，0/1（关注的量编为1）

3. 描述连续变量的分布

• 集中趋势（位置）—中心的度量：均值、中位数、众数
  #看偏度确定选择均值还是中位数，右偏选择中位数，不偏选择均值
  
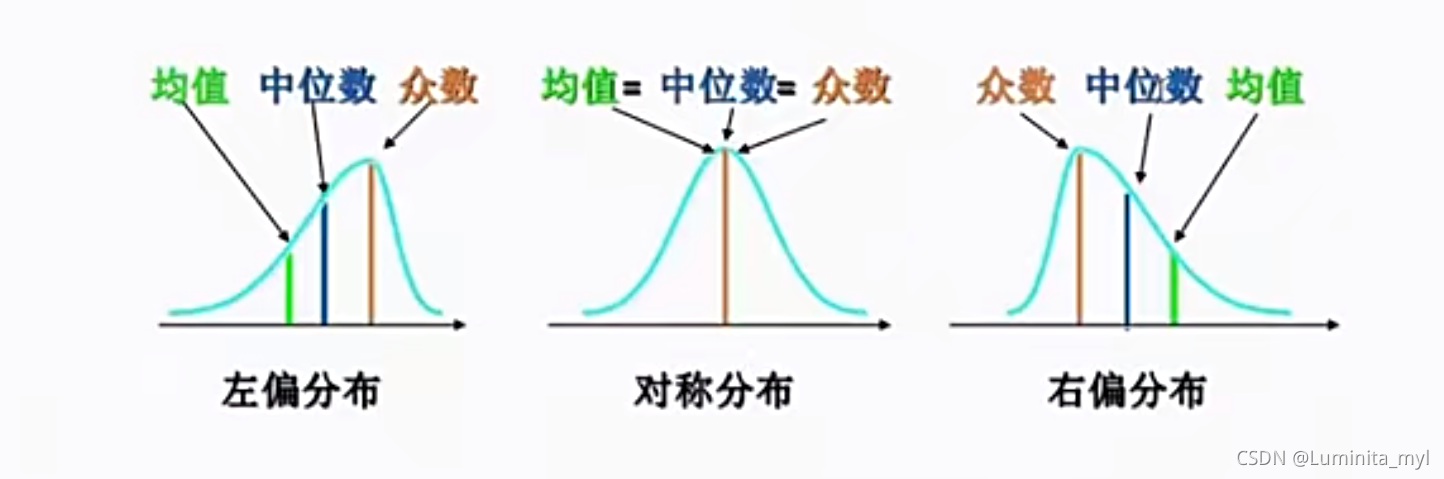
• 离散程度（分散程度）：方差、标准差、极差、四分位差IQR

方差Variance：

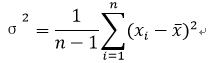
标准差Standard Deviation:

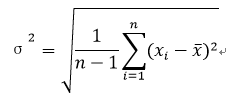
四分位差IQR：上分位数-下分位数

盒须图 ：变量分布、内分位距IQR、异常点

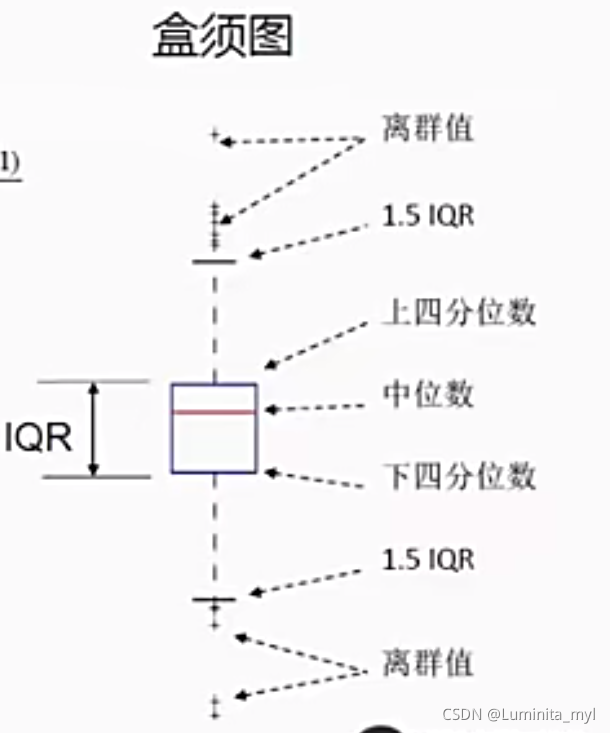
• 偏度（形状）：正态不偏skewness=0、右偏skewness正值

4. 常见连续分布

1）对数正态分布 ：运用广泛，收入的分布，右偏
描述性统计分析：取中位数
建模：取对数
2）伽玛分布：灾难造成损失金额
3）泊松分布：队伍长度
4）正态分布：自然界分布，均值代表中心水平

1.2 描述统计/案例

导入所需的包

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import matplotlib
import seaborn as sns
import os                #os:Operating System操作系统

读取数据

os.chdir(r'D:\python商业实践\《Python数据科学技术详解与商业实践》PDF+源代码+八大案例\《Python数据科学技术详解与商业实践》PDF+源代码+八大案例\源代码\Python_book\4Describe')
snd=pd.read_csv("sndHsPr.csv")
snd.head()

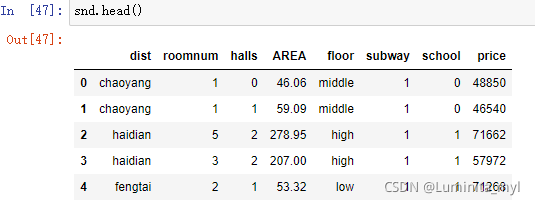
更改区名

district={'fengtai':'丰台区','haidian':'海淀区','chaoyang':'朝阳区','dongcheng':'东城区','shijingshan':'石景山区','xicheng':'西城区'}
snd['district']=snd.dist.map(district)在这里插入代码片

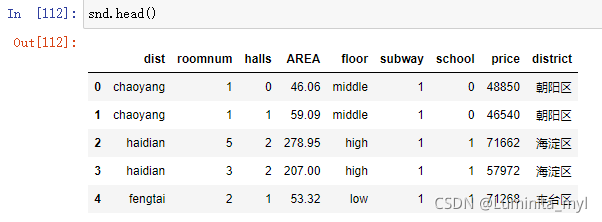
1.2.1 单因子频数：一个分类变量

value_counts() 每个数值的频次

snd.district.value_counts()

• 绘制柱状图.plot(kind='bar')

snd.district.value_counts().plot(kind='bar')   

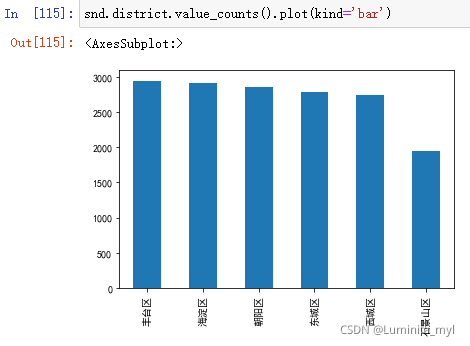
• 绘制饼状图kind='pie'

snd.district.value_counts().plot(kind='pie')    

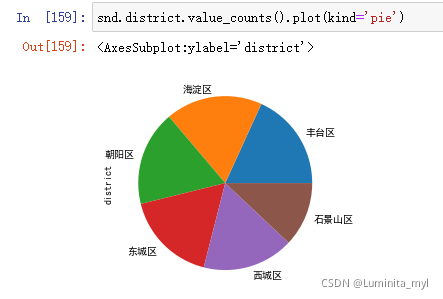
1.2.2 表分析

两个分类变量

pd.crosstab(分类变量1，分类变量2)

生成数据框，频次表

sub_sch=pd.crosstab(snd.district,snd.school)    
sub_sch

• 分类柱形图

pd.crosstab(snd.district,snd.school).plot(kind='bar')

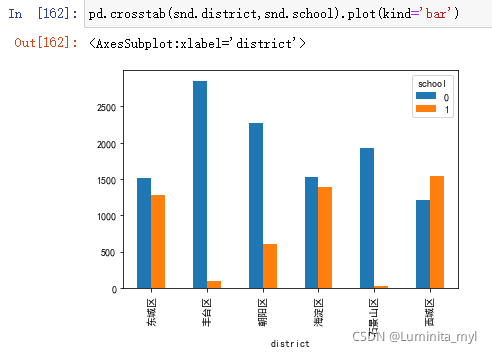
• 堆叠柱形图，可以看出资源分配

t1=pd.crosstab(snd.district,snd.school)
t1.plot(kind='bar',stacked=True)

• 标准化堆叠柱形图
  用于比较两个分类变量是否有关系 ，直观，明显看出资源分配

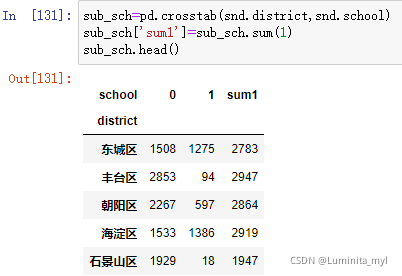
sub_sch=pd.crosstab(snd.district,snd.school)
sub_sch['sum1']=sub_sch.sum(1)                  #1代表列，汇总出一列
sub_sch.head()

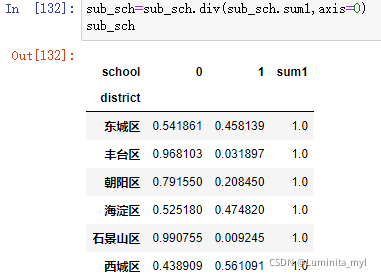
sub_sch=sub_sch.div(sub_sch.sum1,axis=0)    #按行求百分比
sub_sch

sub_sch[[0,1]].plot(kind='bar',stacked=True)

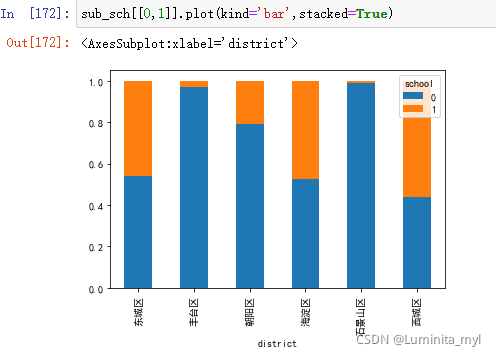
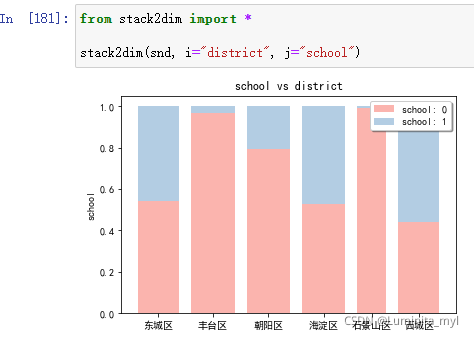
• 两个维度标准化的堆积柱状图，柱形的宽度代表数量，更直观。

def stack2dim (raw,i,j,rotation=0,location='upper right'):

raw：pandas的DataFrame数据框
i、j：两个分类变量名称，横纵轴名称
rotation：水平标签旋转角度，默认水平方向，若标签过长，可设置一定角度，如rotation=40
location：分类标签位置，如果被主题图形挡住，可更改为‘upper left’

需要调用函数*

from stack2dim import *
stack2dim(snd, i="district", j="school")      

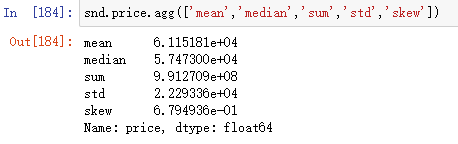
1.2.3 单连续变量描述

snd.price.agg(['mean','median','sum','std','skew'])    #得多个统计量

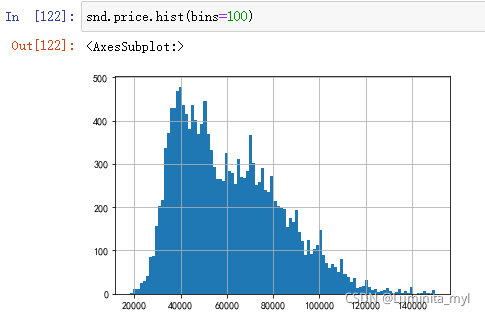
绘制直方图，查看分布情况，类似正态分布

snd.price.hist(bins=100)            #bins为分组数

snd.price.mean()     #均值
snd.price.median()   #中位数
snd.price.std()      #标准差
snd.price.skew()     #偏度

snd.price.quantile([0.01,0.5,0.99])      #取分位点

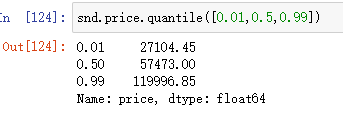
1.2.4 分类汇总

一个分类变量、一个连续变量统计量
groupby() 分类汇总

snd.price.groupby(snd.district).mean()    #取连续变量的均值，可替换

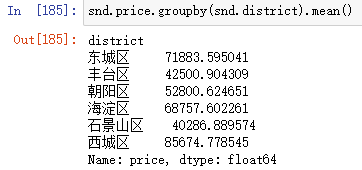
• 柱形图

snd.price.groupby(snd.district).mean().plot(kind='bar')

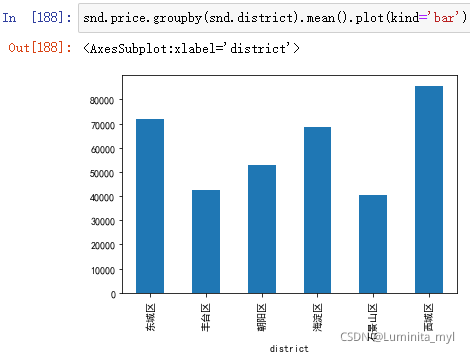
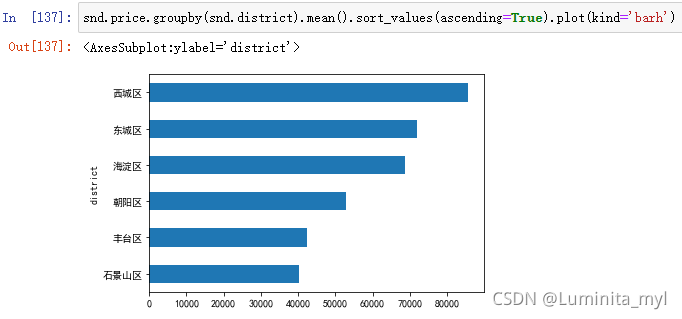
• 排序可得条形图 kind='barh'加h为横向条形图
  
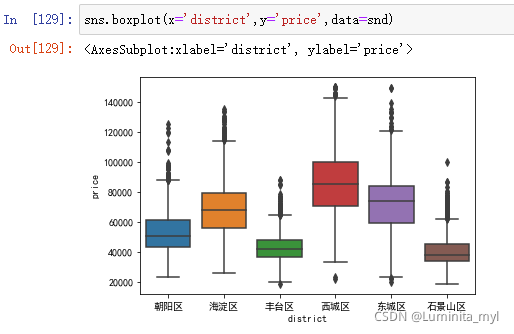
• 分类盒须图
  体现分类变量和连续变量关系，比较不同分类水平上，连续变量的变化情况，比较中位数，直观。

sns.boxplot(x='district',y='price',data=snd)

1.2.5 汇总表

两个分类变量（分别在x、y轴）、一个连续变量统计量
pivot_table()

snd.pivot_table(values='price',index='district',columns='school',aggfunc=np.mean)    #mean是numpy的函数  np.mean

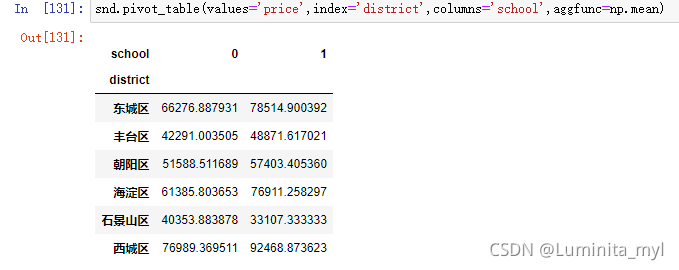
柱形图

snd.pivot_table(values='price',index='district',columns='school',aggfunc=np.mean).plot(kind='bar')

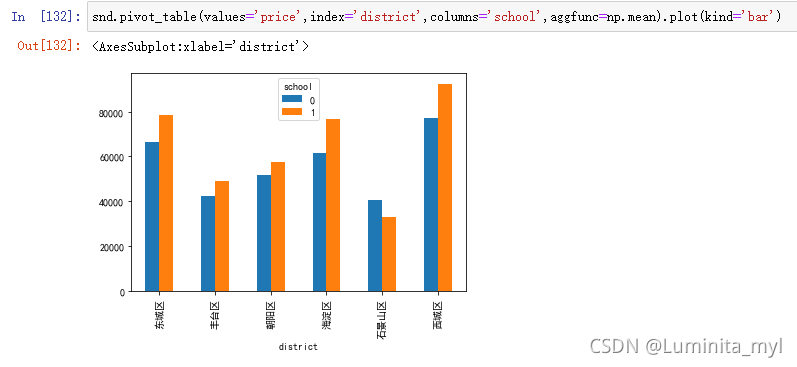
1.2.5 时间序列——双轴图

按年度汇总GDP，计算GDP增长率。GDP为柱子，GDP增长率为线
导入gdp数据

gdp=pd.read_csv('gdp_gdpcr.csv',encoding='gbk')

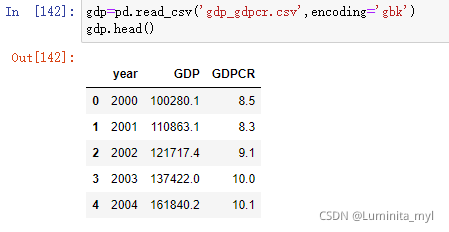
x=list(gdp.year)
GDP=list(gdp.GDP)
GDPCR=list(gdp.GDPCR)
fig=plt.figure()                           #设置绘图区域

ax1=fig.add_subplot(111)     
ax1.bar(x,GDP)                             #主轴表示GDP
ax1.set_ylabel('GDP')                      #设置主轴标题
ax1.set_title("GDP of China(2000-2017)")   #设置图标题
ax1.set_xlim(2000,2018)                    #设置横坐标数值范围

ax2=ax1.twinx()                            #拷贝的副轴
ax2.plot(x,GDPCR,'r')                      #‘r’表示为红色red
ax2.set_ylabel('Increase Ratio')
ax2.set_xlabel('Year')

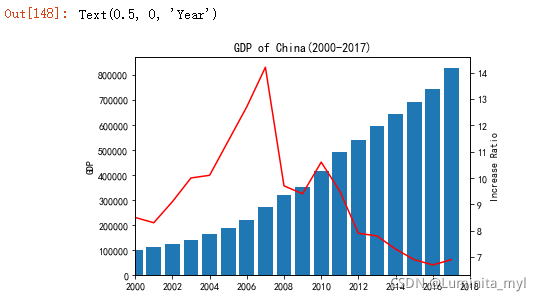
##所有代码要写在一个cell，否则得不到图

附：
若横坐标乱码，显示出方块，可能原因是默认字体不能打印汉字，修改字体加入以下代码

from pylab import mpl
mpl.rcParams['font.sans-serif']=['SimHei']    #指定默认字体 SimHei表示简体中文
mpl.rcParams['axes.unicode_minus']=False      #解决横坐标显示方块的问题
snd.district.value_counts().plot(kind='bar')  

2 绘图原理

数据->信息->相对关系->图像

表达关联性的图标
一个分类一个连续：盒须图
多分类：堆叠柱形图
两个连续变量：散点图