[人工智能]激活函数汇总，包含公式、求导过程以及numpy实现，妥妥的万字干货

1、激活函数的实现

1.1 sigmoid

1.1.1 函数

函数：$f(x)=\frac{1}{1+e^{?x}}$

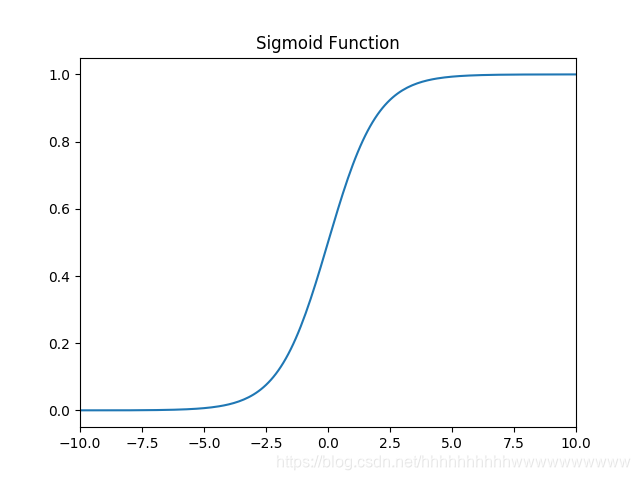
1.1.2 导数

求导过程：

根据：$\left(\frac{u}{v}\right){}^{\prime }=\frac{u^{\prime }v?u{v}^{\prime }}{v^2}$
$$\begin{array}{rl}f(x{)}^{\prime }& ={\left(\frac{1}{1+e^{?x}}\right)}^{\prime }\\ & =\frac{1^{\prime }\times \left(1+e^{?x}\right)?1\times {\left(1+e^{?x}\right)}^{\prime }}{{\left(1+e^{?x}\right)}^2}\\ & =\frac{e^{?x}}{{\left(1+e^{?x}\right)}^2}\\ & =\frac{1+e^{?x}?1}{{\left(1+e^{?x}\right)}^2}\\ & =\left(\frac{1}{1+e^{?x}}\right)\left(1?\frac{1}{1+e^{?x}}\right)\\ & =f(x)(1?f(x))\end{array}$$

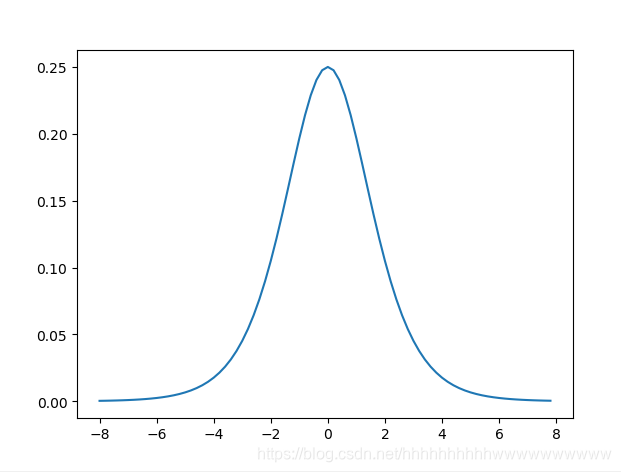
1.1.3 代码实现

import numpy as np

class Sigmoid():
    def __call__(self, x):
        return 1 / (1 + np.exp(-x))

    def gradient(self, x):
        return self.__call__(x) * (1 - self.__call__(x))

1.2 softmax

1.2.1 函数

softmax用于多分类过程中，它将多个神经元的输出，映射到（0,1）区间内，可以看成概率来理解，从而来进行多分类！

假设我们有一个数组，V，Vi表示V中的第i个元素，那么这个元素的softmax值就是:
$$S_i=\frac{e^i}{{\sum }_j{e}^j}$$
更形象的如下图表示：

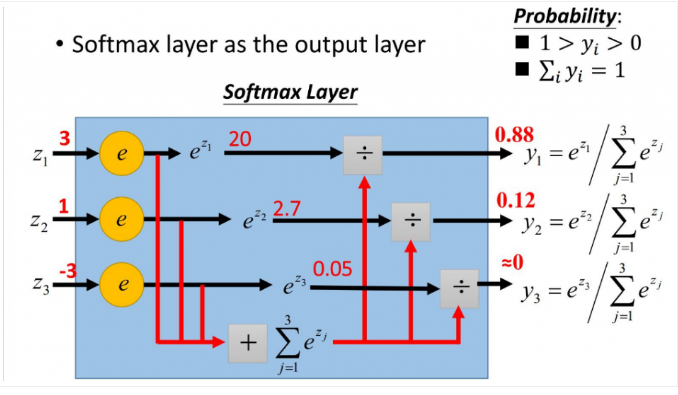
$$\begin{gathered} y1=\frac{e^{z_1}}{e^{z_1}+e^{z_2}+e^{z_3}} \\ y2=\frac{e^{z_2}}{e^{z_1}+e^{z_2}+e^{z_3}} \\ y3=\frac{e^{z_3}}{e^{z_1}+e^{z_2}+e^{z_3}} \\ \text{\hspace{1em}(1)} \end{gathered}$$
要使用梯度下降，就需要一个损失函数，一般使用交叉熵作为损失函数，交叉熵函数形式如下：
$$Loss=?\sum _i{y}_{i}ln{a}_i\text{\hspace{1em}(2)}$$

1.2.2 导数

求导分为两种情况。

第一种j=i：
$$S_i=\frac{e^i}{{\sum }_j{e}^j}=\frac{e^i}{{\sum }_i{e}^i}$$
推导过程如下：
$$\begin{array}{rlr}{f}^{\prime }& ={\left(\frac{e^i}{{\sum }_i{e}^i}\right)}^{\prime }& \\ & =\frac{\left(e^i\right)\times {\sum }_i{e}^i?e^i\times e^i}{{\left({\sum }_i{e}^i\right)}^2}& \\ & =\frac{e^i}{{\sum }_i{e}^i}?\frac{e^i}{{\sum }_i{e}^i}\times \frac{e^i}{{\sum }_i{e}^i}& \\ & =\frac{e^i}{{\sum }_i{e}^i}\left(1?\frac{e^i}{{\sum }_i{e}^i}\right)& \\ & =f(1?f)& \end{array}$$

1.2.3 代码实现

import numpy as np
class Softmax():
    def __call__(self, x):
        e_x = np.exp(x - np.max(x, axis=-1, keepdims=True))
        return e_x / np.sum(e_x, axis=-1, keepdims=True)

    def gradient(self, x):
        p = self.__call__(x)
        return p * (1 - p)

1.3 tanh

1.3.1 函数

$$tanh(x)=\frac{e^x?e^{?x}}{e^x+e^{?x}}$$

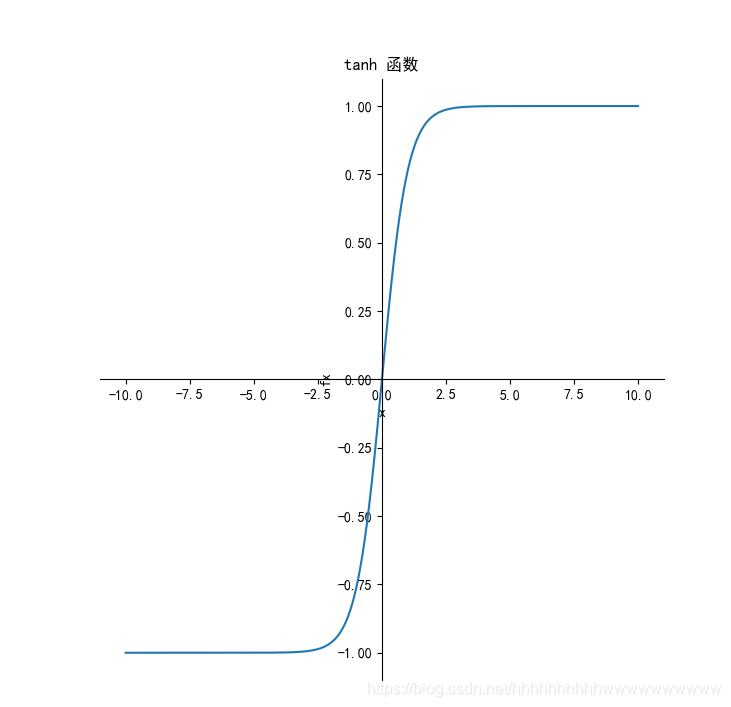
1.3.2 导数

求导过程：
$$\begin{array}{rl}\tanh (x{)}^{\prime }& ={\left(\frac{e^x?e^{?x}}{e^x+e^{?x}}\right)}^{\prime }\\ & =\frac{{\left(e^x?e^{?x}\right)}^{\prime }\left(e^x+e^{?x}\right)?\left(e^x?e^{?x}\right){\left(e^x+e^{?x}\right)}^{\prime }}{{\left(e^x+e^{?x}\right)}^2}\\ & =\frac{{\left(e^x+e^{?x}\right)}^2?{\left(e^x?e^{?x}\right)}^2}{{\left(e^x+e^{?x}\right)}^2}\\ & =1?{\left(\frac{e^x?e^{?x}}{e^x+e^{?x}}\right)}^2\\ & =1?\tanh (x{)}^2\end{array}$$

1.3.3 代码实现

import numpy as np
class TanH():
    def __call__(self, x):
        return 2 / (1 + np.exp(-2*x)) - 1

    def gradient(self, x):
        return 1 - np.power(self.__call__(x), 2)

1.4 relu

1.4.1 函数

$$f(x)=\max (0,x)$$

1.4.2 导数

$$f^{\prime }(x)=\{\begin{array}{cc}1& \text{?if?}(x>0)\\ 0& \text{?if?}(x<=0)\end{array}$$

1.4.3 代码实现

import numpy as np
class ReLU():
    def __call__(self, x):
        return np.where(x >= 0, x, 0)

    def gradient(self, x):
        return np.where(x >= 0, 1, 0)

1.5 leakyrelu

1.5.1 函数

$$f(x)=\max (ax,x)$$

1.5.2 导数

$$f^{\prime }(x)=\{\begin{array}{cl}1& \text{?if?}(x>0)\\ a& \text{?if?}(x<=0)\end{array}$$

1.5.3 代码实现

import numpy as np
class LeakyReLU():
    def __init__(self, alpha=0.2):
        self.alpha = alpha

    def __call__(self, x):
        return np.where(x >= 0, x, self.alpha * x)

    def gradient(self, x):
        return np.where(x >= 0, 1, self.alpha)

1.6 ELU

1.61 函数

$$f(x)=\{\begin{array}{cl}x,& \text{?if?}x\ge 0\\ a\left(e^x?1\right),& \text{?if?}(x<0)\end{array}$$

1.6.2 导数

当x>=0时，导数为1。

当x<0时，导数的推导过程：
$$\begin{array}{rl}& \\ f(x{)}^{\prime }& ={\left(a\left(e^x?1\right)\right)}^{\prime }\\ & =a{e}^x\\ & =a(e^x?1)+a\\ & =f(x)+a=a{e}^x\end{array}$$
所以，完整的导数为：
$$f^{\prime }=\{\begin{array}{cll}1& \text{?if?}& x\ge 0\\ f(x)+a=a{e}^x& \text{?if?}& x<0\end{array}$$

1.6.3 代码实现

import numpy as np
class ELU():
    def __init__(self, alpha=0.1):
        self.alpha = alpha 

    def __call__(self, x):
        return np.where(x >= 0.0, x, self.alpha * (np.exp(x) - 1))

    def gradient(self, x):
        return np.where(x >= 0.0, 1, self.__call__(x) + self.alpha)

1.7 selu

1.7.1 函数

$$\mathrm{selu}(x)=\lambda \{\begin{array}{ll}x& \text{?if?}(x>0)\\ \alpha e^x?\alpha & \text{?if?}(x?0)\end{array}$$

1.7.2 导数

$${\mathrm{selu}}^{\prime }(x)=\lambda \{\begin{array}{ll}1& x>0\\ \alpha e^x& ?0\end{array}$$

1.7.3 代码实现

import numpy as np
class SELU():
    # Reference : https://arxiv.org/abs/1706.02515,
    # https://github.com/bioinf-jku/SNNs/blob/master/SelfNormalizingNetworks_MLP_MNIST.ipynb
    def __init__(self):
        self.alpha = 1.6732632423543772848170429916717
        self.scale = 1.0507009873554804934193349852946 

    def __call__(self, x):
        return self.scale * np.where(x >= 0.0, x, self.alpha*(np.exp(x)-1))

    def gradient(self, x):
        return self.scale * np.where(x >= 0.0, 1, self.alpha * np.exp(x))

1.8 softplus

1.81 函数

$$\mathrm{Softplus}(x)=\log \left(1+e^x\right)$$

1.8.2 导数

log默认的底数是$e$
$$f^{\prime }(x)=\frac{e^x}{(1+e^x)\ln e}=\frac{1}{1+e^{?x}}=\sigma (x)$$

1.8.3 代码实现

import numpy as np
class SoftPlus():
    def __call__(self, x):
        return np.log(1 + np.exp(x))

    def gradient(self, x):
        return 1 / (1 + np.exp(-x))

1.9 Swish

1.9.1 函数

$$f(x)=x?\mathrm{sigmoid}(\beta x)$$

1.9.2 导数

$$\begin{array}{rl}{f}^{\prime }(x)& =\sigma (\beta x)+\beta x?\sigma (\beta x)(1?\sigma (\beta x))\\ & =\sigma (\beta x)+\beta x?\sigma (\beta x)?\beta x?\sigma (\beta x{)}^2\\ & =\beta x?\sigma (x)+\sigma (\beta x)(1?\beta x?\sigma (\beta x))\\ & =\beta f(x)+\sigma (\beta x)(1?\beta f(x))\end{array}$$

1.9.3 代码实现

import numpy as np


class Swish(object):
    def __init__(self, b):
        self.b = b

    def __call__(self, x):
        return x * (np.exp(self.b * x) / (np.exp(self.b * x) + 1))

    def gradient(self, x):
        return self.b * x / (1 + np.exp(-self.b * x)) + (1 / (1 + np.exp(-self.b * x)))(
            1 - self.b * (x / (1 + np.exp(-self.b * x))))

1.10 Mish

1.10.1 函数

$$f(x)=x?\tanh \left(\ln \left(1+e^x\right)\right)$$

1.10.2 导数

$$\begin{array}{c}{f}^{\prime }(x)={\mathrm{sech}}^2(\mathrm{soft}\mathrm{plus}(x))x\mathrm{sigmoid}(x)+\frac{f(x)}{x}\\ =\Delta (x)swi\mathrm{sh}(x)+\frac{f(x)}{x}\end{array}$$
where softplus $(x)=\ln \left(1+e^x\right)$ and sigmoid $(x)=1/\left(1+e^{?x}\right)$.

1.10.3 代码实现

import numpy as np


def sech(x):
    """sech函数"""
    return 2 / (np.exp(x) + np.exp(-x))


def sigmoid(x):
    """sigmoid函数"""
    return 1 / (1 + np.exp(-x))


def soft_plus(x):
    """softplus函数"""
    return np.log(1 + np.exp(x))


def tan_h(x):
    """tanh函数"""
    return (np.exp(x) - np.exp(-x)) / (np.exp(x) + np.exp(-x))


class Mish:

    def __call__(self, x):
        return x * tan_h(soft_plus(x))

    def gradient(self, x):
        return sech(soft_plus(x)) * sech(soft_plus(x)) * x * sigmoid(x) + tan_h(soft_plus(x))

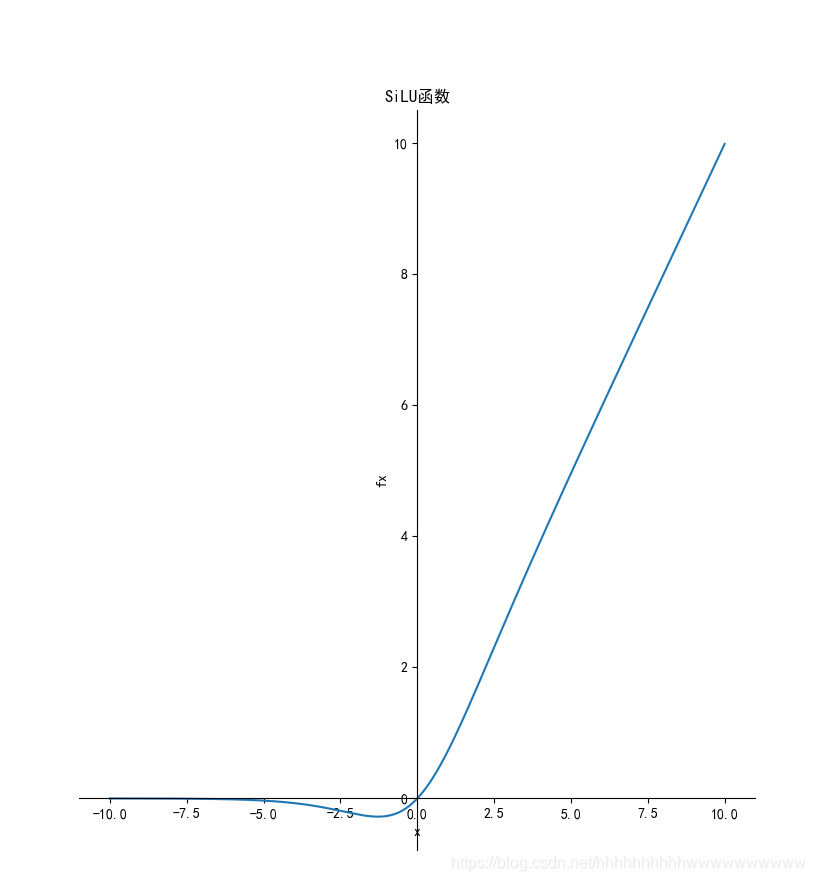
1.11 SiLU

1.11.1 函数

$$f(x)=x\times sigmoid(x)$$

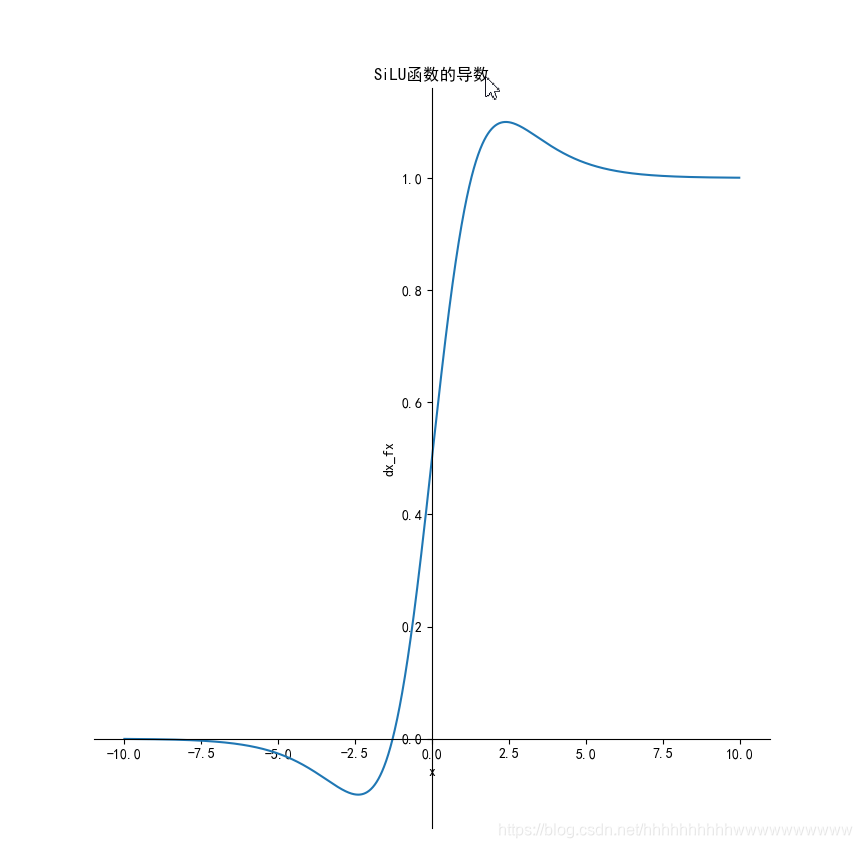
1.11.2 导数

推导过程
$$\begin{array}{rl}& f(x{)}^{\prime }=(x?sigmoid(x){)}^{\prime }\\ & =sigmoid(x)+x?(sigmoid(x)(1?sigmoid(x))\\ & =sigmoid(x)+x?sigmoid(x)?x?sigmoi{d}^2(x)\\ & =f(x)+\mathrm{sigmoid}(x)(1?f(x))\end{array}$$

1.11.3 代码实现

import numpy as np


def sigmoid(x):
    """sigmoid函数"""
    return 1 / (1 + np.exp(-x))


class SILU(object):

    def __call__(self, x):
        return x * sigmoid(x)

    def gradient(self, x):
        return self.__call__(x) + sigmoid(x) * (1 - self.__call__(x))

1.12 完整代码

定义一个activation_function.py,将下面的代码复制进去，到这里激活函数就完成了。

import numpy as np


# Collection of activation functions
# Reference: https://en.wikipedia.org/wiki/Activation_function

class Sigmoid():
    def __call__(self, x):
        return 1 / (1 + np.exp(-x))

    def gradient(self, x):
        return self.__call__(x) * (1 - self.__call__(x))


class Softmax():
    def __call__(self, x):
        e_x = np.exp(x - np.max(x, axis=-1, keepdims=True))
        return e_x / np.sum(e_x, axis=-1, keepdims=True)

    def gradient(self, x):
        p = self.__call__(x)
        return p * (1 - p)


class TanH():
    def __call__(self, x):
        return 2 / (1 + np.exp(-2 * x)) - 1

    def gradient(self, x):
        return 1 - np.power(self.__call__(x), 2)


class ReLU():
    def __call__(self, x):
        return np.where(x >= 0, x, 0)

    def gradient(self, x):
        return np.where(x >= 0, 1, 0)


class LeakyReLU():
    def __init__(self, alpha=0.2):
        self.alpha = alpha

    def __call__(self, x):
        return np.where(x >= 0, x, self.alpha * x)

    def gradient(self, x):
        return np.where(x >= 0, 1, self.alpha)


class ELU(object):
    def __init__(self, alpha=0.1):
        self.alpha = alpha

    def __call__(self, x):
        return np.where(x >= 0.0, x, self.alpha * (np.exp(x) - 1))

    def gradient(self, x):
        return np.where(x >= 0.0, 1, self.__call__(x) + self.alpha)


class SELU():
    # Reference : https://arxiv.org/abs/1706.02515,
    # https://github.com/bioinf-jku/SNNs/blob/master/SelfNormalizingNetworks_MLP_MNIST.ipynb
    def __init__(self):
        self.alpha = 1.6732632423543772848170429916717
        self.scale = 1.0507009873554804934193349852946

    def __call__(self, x):
        return self.scale * np.where(x >= 0.0, x, self.alpha * (np.exp(x) - 1))

    def gradient(self, x):
        return self.scale * np.where(x >= 0.0, 1, self.alpha * np.exp(x))


class SoftPlus(object):
    def __call__(self, x):
        return np.log(1 + np.exp(x))

    def gradient(self, x):
        return 1 / (1 + np.exp(-x))


class Swish(object):
    def __init__(self, b):
        self.b = b

    def __call__(self, x):
        return x * (np.exp(self.b * x) / (np.exp(self.b * x) + 1))

    def gradient(self, x):
        return self.b * x / (1 + np.exp(-self.b * x)) + (1 / (1 + np.exp(-self.b * x)))(
            1 - self.b * (x / (1 + np.exp(-self.b * x))))


def sech(x):
    """sech函数"""
    return 2 / (np.exp(x) + np.exp(-x))


def sigmoid(x):
    """sigmoid函数"""
    return 1 / (1 + np.exp(-x))


def soft_plus(x):
    """softplus函数"""
    return np.log(1 + np.exp(x))


def tan_h(x):
    """tanh函数"""
    return (np.exp(x) - np.exp(-x)) / (np.exp(x) + np.exp(-x))


class Mish:

    def __call__(self, x):
        return x * tan_h(soft_plus(x))

    def gradient(self, x):
        return sech(soft_plus(x)) * sech(soft_plus(x)) * x * sigmoid(x) + tan_h(soft_plus(x))

class SILU(object):

    def __call__(self, x):
        return x * sigmoid(x)

    def gradient(self, x):
        return self.__call__(x) + sigmoid(x) * (1 - self.__call__(x))

参考公式
$(C{)}^{\prime }=0$
${\left(a^x\right)}^{\prime }=a^x\ln a$
${\left(x^{\mu }\right)}^{\prime }=\mu x^{\mu ?1}$
${\left(e^x\right)}^{\prime }=e^x$
$(\sin x{)}^{\prime }=\cos x$
${\left({\log }_{a}x\right)}^{\prime }=\frac{1}{x\ln a}$
$(\cos x{)}^{\prime }=?\sin x$
$(\ln x{)}^{\prime }=\frac{1}{x}$
$(\tan x{)}^{\prime }={\sec }^{2}x$
$(\arcsin x{)}^{\prime }=\frac{1}{\sqrt{1?x^2}}$
$(\cot x{)}^{\prime }=?{\csc }^{2}x$
$(\arccos x{)}^{\prime }=?\frac{1}{\sqrt{1?x^2}}$
$(\sec x{)}^{\prime }=\sec x?\tan x$
$(\arctan x{)}^{\prime }=\frac{1}{1+x^2}$
$(\csc x{)}^{\prime }=?\csc x?\cot x$
$(\mathrm{arccot}x{)}^{\prime }=?\frac{1}{1+x^2}$

双曲正弦: $\sinh x=\frac{e^x?e^{?x}}{2}$
双曲余弦: $\cosh x=\frac{e^x+e^{?x}}{2}$
双曲正切: $\tanh x=\frac{\sinh x}{\cosh x}=\frac{e^x?e^{?x}}{e^x+e^{?x}}$
双曲余切: $\coth x=\frac{1}{\tanh x}=\frac{e^x+e^{?x}}{e^x?e^{?x}}$
双曲正割： $\mathrm{sech}x=\frac{1}{\cosh x}=\frac{2}{e^x+e^{?x}}$
双曲余割： $\mathrm{csch}x=\frac{1}{\sinh x}=\frac{2}{e^x?e^{?x}}$