李宏毅机器学习13、14-深度学习和反向传播
深度学习的步骤
- Step1：神经网络（Neural network）
- Step2：模型评估（Goodness of function）
- Step3：选择最优函数（Pick best function）
Step1：神经网络（Neural network）
神经元之间的连接方式
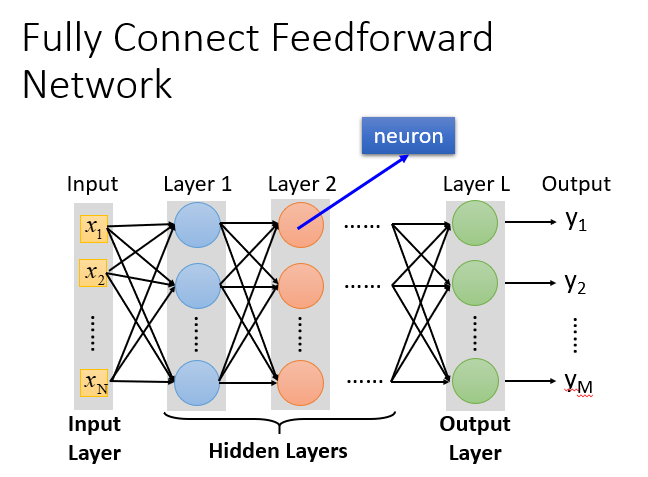
全连接前馈神经网络
神经网络可以有很多不同的连接方式，会产生不同的结构（structure）。全连接前馈神经网络是其中的一种。
全链接和前馈的理解
前馈（feedforward）也可以称为前向，从信号流向来理解就是输入信号进入网络后，信号流动是单向的，即信号从前一层流向后一层，一直到输出层，其中任意两层之间的连接并没有反馈（feedback），亦即信号没有从后一层又返回到前一层。
- 全链接Fully Connect：layer1与layer2之间两两都有连接；
- 前馈Feedforward：传递的方向是由前往后传。
全连接前馈神经网络结构
- 输入层（Input Layer）：1层
- 隐藏层（Hidden Layer）：N层
- 输出层（Output Layer）：1层
深度Deep
Deep = Many hidden layer。（留下一个疑问为什么deep好（相对少的神经元多层）而不是fat（单层超多神经元）好？）
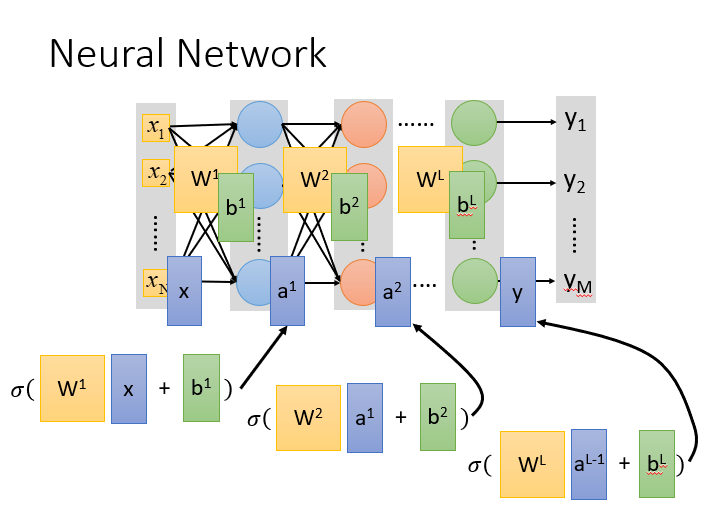
矩阵运算加速
本质：隐藏层-特征提取器
把隐藏层通过特征提取来替代原来的特征工程，最后一个隐藏层输出的就是一组新的特征（相当于黑箱操作）。而对于输出层，其实是把前面的隐藏层的输出当做输入（经过特征提取得到的一组最好的特征）然后通过一个多分类器（可以是softmax函数）得到最后的输出
y
y
y。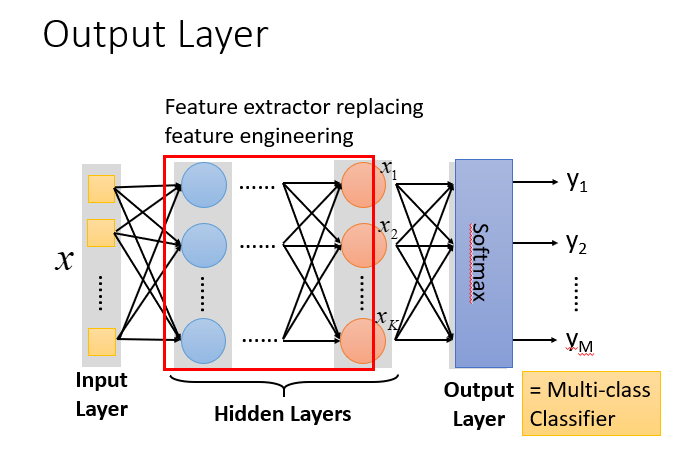 
问题
-
多少层？ 每层有多少神经元？
用尝试加上直觉的方法来进行调试。对于有些机器学习相关的问题，我们一般用特征工程来提取特征，但是对于深度学习，我们只需要设计神经网络模型的结构。
-
结构可以自动确定吗？
有方法可以让机器自动找到神经网络的结构的，比如进化人工神经网络（Evolutionary Artificial Neural Networks） 。
-
可以设计网络结构吗？
可以的，比如 CNN卷积神经网络（Convolutional Neural Network ）。
在这里插入图片描述
Step2：模型评估（Goodness of function）
一般采用损失函数来反应模型的好差，比如对于用于分类的神经网络来说，我们采用交叉熵（cross entropy）函数来对 y y y和 y ^ \hat{y} y^?的损失进行计算，调整参数，让交叉熵越小越好。
总体损失
不单单要计算一笔数据的，而是要计算整体所有训练数据的损失加起来，得到一个总体损失
L
L
L。然后在function set里面找到一组函数能最小化这个总体损失
L
L
L，或者说找一组神经网络的参数
θ
\theta
θ，来最小化总体损失
L
L
L。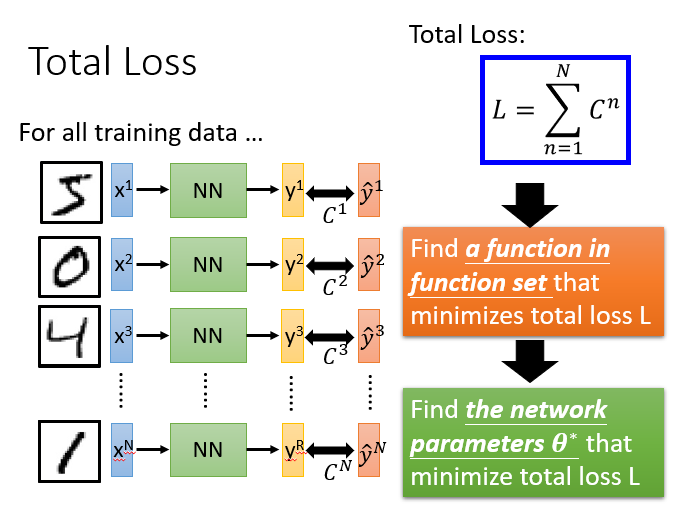
Step3：选择最优函数（Pick best function）
用梯度下降的方式找到最优的函数和最好的一组参数。
具体流程：
- θ \theta θ是一组包含权重和偏差的参数集合，随机找一个初始值；
- 计算一下每个参数对应偏微分，得到的一个偏微分的集合 ? L \nabla{L} ?L（梯度）；
- 利用这些偏微分，不断更新梯度得到新的参数，这样不断反复进行；
- 最终能得到一组最好的参数使得损失函数的值最小。
反向传播Backpropagation
反向传播Backpropagation是一个有效率的梯度下降算法。
链式法则
- 连锁影响(可以看出x会影响y，y会影响z)
- BP主要用到了chain rule
取出一个Neuron进行分析
可以把计算梯度分成两个部分：
- 计算 ? z ? w \frac{\partial z}{\partial w} ?w?z?（Forward pass的部分）
- 计算 ? l ? z \frac{\partial l}{\partial z} ?z?l?( Backward pass的部分 )
如下图所示，我们的目标是要计算 ? z ? w \frac{\partial z}{\partial w} ?w?z?（Forward pass的部分）和计算 ? l ? z \frac{\partial l}{\partial z} ?z?l? ( Backward pass的部分 )，然后把 ? z ? w \frac{\partial z}{\partial w} ?w?z?和 ? l ? z \frac{\partial l}{\partial z} ?z?l?相乘，得到 ? l ? w \frac{\partial l}{\partial w} ?w?l?。然后就可以得到神经网络中所有的参数，用梯度下降不断更新，得到损失最小的函数 。
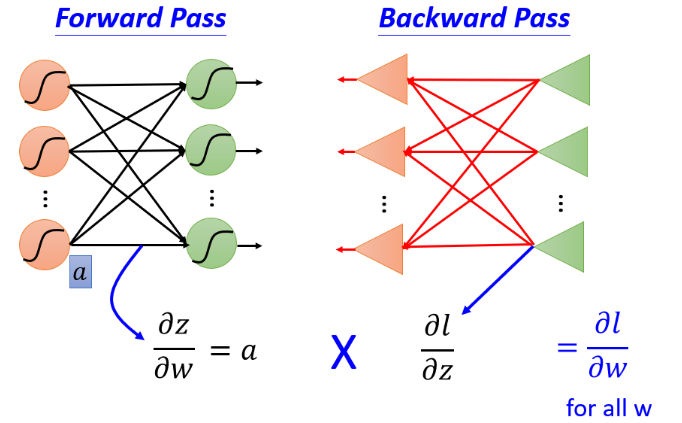
forward pass-计算 ? z ? w \frac{\partial z}{\partial w} ?w?z?
根据求微分原理，forward pass的运算规律就是：
?
z
?
w
1
=
x
1
?
z
?
w
2
=
x
2
\frac{\partial z}{\partial w_1} = x_1 \\ \frac{\partial z}{\partial w_2} = x_2
?w1??z?=x1??w2??z?=x2?
所以计算得到的
x
1
x_1
x1?和
x
2
x_2
x2?恰好就是输入的
x
1
x_1
x1?和
x
2
x_2
x2? 。
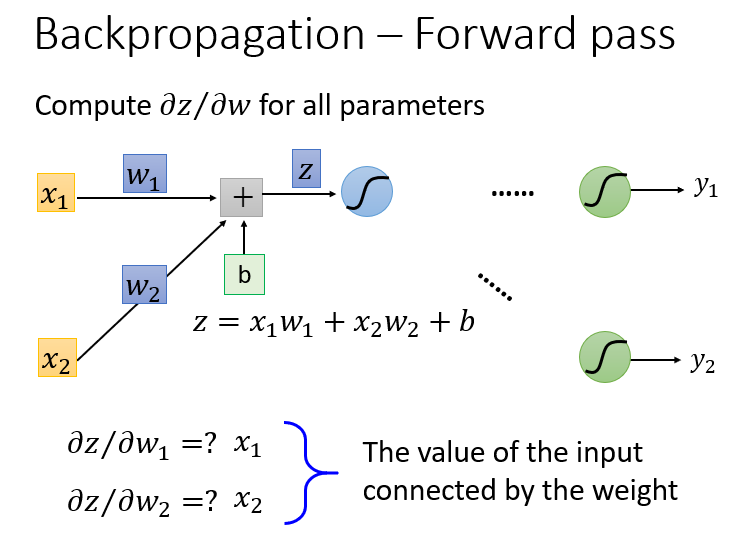
也就是说，对于每一层的 ? z ? w \frac{\partial z}{\partial w} ?w?z?都是其输入：
backward pass-计算 ? l ? z \frac{\partial l}{\partial z} ?z?l?
计算所有激活函数的偏微分，激活函数有很多，这里使用Sigmoid函数为例：
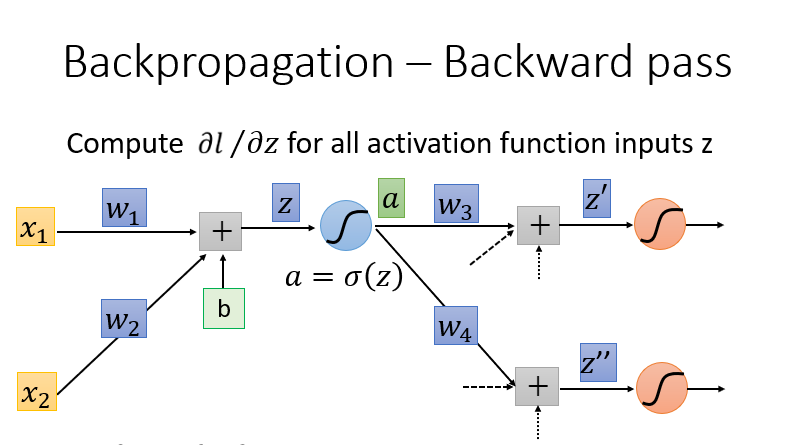
使用链式法则（Chain Rule）的case1，可以把
?
l
?
z
\frac{\partial l}{\partial z}
?z?l?拆分为：
?
l
?
z
=
?
a
?
z
?
l
?
a
\frac{\partial l}{\partial z} = \frac{\partial a}{\partial z}\frac{\partial l}{\partial a}
?z?l?=?z?a??a?l?
进一步根据链式法则case2计算过程如下：
?
l
?
z
=
?
a
?
z
?
l
?
a
?
σ
′
(
z
)
?
l
?
a
=
?
z
′
?
a
?
l
?
z
′
+
?
z
′
′
?
a
?
l
?
z
′
′
\frac{\partial l}{\partial z} = \frac{\partial a}{\partial z}\frac{\partial l}{\partial a} \Rightarrow {\sigma}'(z) \frac{\partial l}{\partial a} = \frac{\partial z'}{\partial a}\frac{\partial l}{\partial z'} +\frac{\partial z''}{\partial a}\frac{\partial l}{\partial z''}
?z?l?=?z?a??a?l??σ′(z)?a?l?=?a?z′??z′?l?+?a?z′′??z′′?l?
根据forward pass的结论得到：
则 ? l ? z \frac{\partial l}{\partial z} ?z?l?式子为：
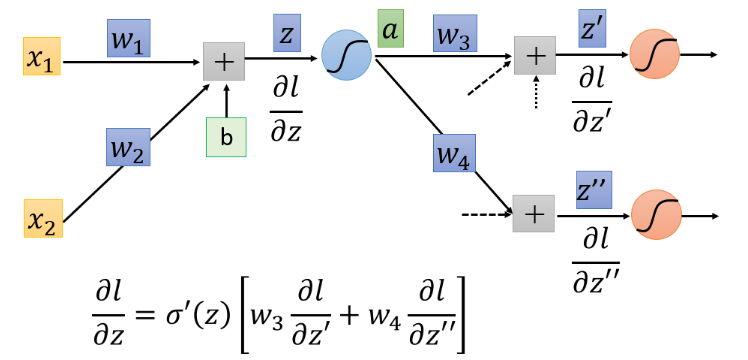
观察这个式子，我们可以反向看待一下：
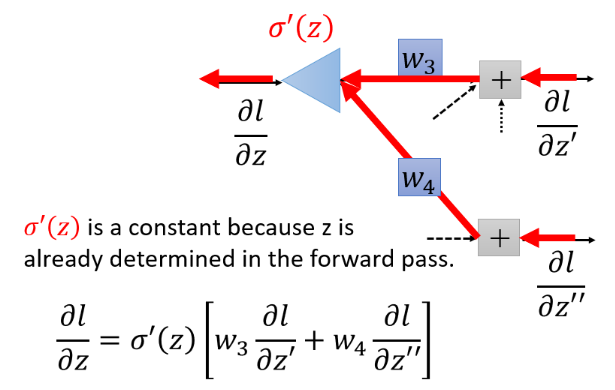
如何求 ? l ? z ′ \frac{\partial l}{\partial z'} ?z′?l?和 ? l ? z ′ ′ \frac{\partial l}{\partial z''} ?z′′?l?呢？
-
case1 该层后直接接到output layer
假设 ? l ? z ′ \frac{\partial l}{\partial z'} ?z′?l?和 ? l ? z ′ ′ \frac{\partial l}{\partial z''} ?z′′?l?是最后一层的隐藏层，那么y1与y2是输出值，可以根据损失函数直接计算得出结果 ：
-
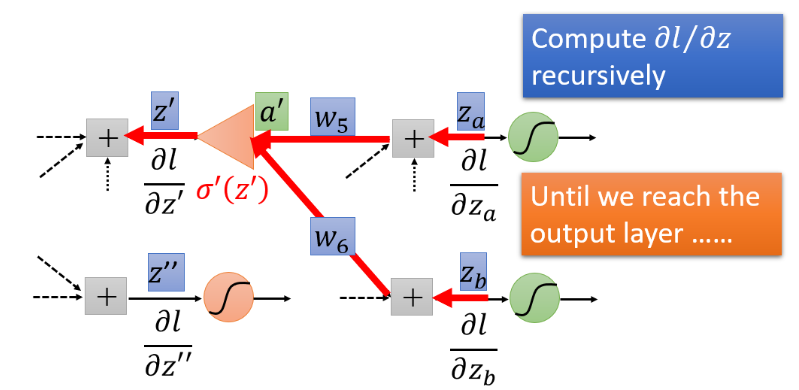
case2 该层后还有隐藏层，而不是output layer
但是如果不是最后一层，计算 ? l ? z ′ \frac{\partial l}{\partial z'} ?z′?l?和 ? l ? z ′ ′ \frac{\partial l}{\partial z''} ?z′′?l?需要继续往后一直通过链式法则算下去。继续乘 w 5 w_5 w5?和 w 6 w_6 w6?得到 ? l ? z ′ \frac{\partial l}{\partial z'} ?z′?l?，如果 ? l ? z a \frac{\partial l}{\partial z_a} ?za??l?和 ? l ? z b \frac{\partial l}{\partial z_b} ?zb??l?仍然不知道，那么就继续往后面层计算，一直到碰到输出值（case1），得到输出值之后再反向往输入方向传。
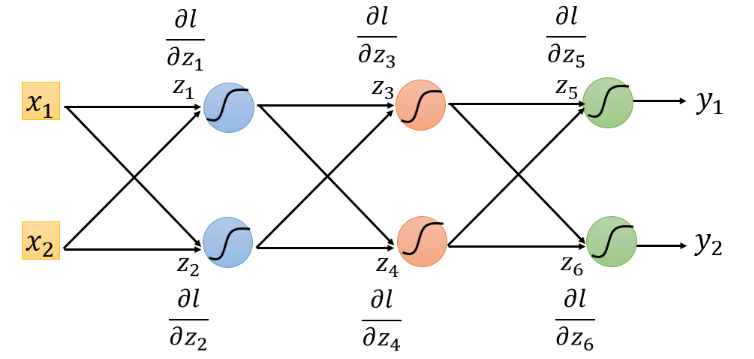对上图，可以从最后一个
?
l
?
z
5
\frac{\partial l}{\partial z_5}
?z5??l?和
?
l
?
z
6
\frac{\partial l}{\partial z_6}
?z6??l?看，因为
?
l
?
z
5
\frac{\partial l}{\partial z_5}
?z5??l?和
?
l
?
z
6
\frac{\partial l}{\partial z_6}
?z6??l?可以通过output求出来，然后继续往前（反向的前）求
?
l
?
z
3
\frac{\partial l}{\partial z_3}
?z3??l?和
?
l
?
z
4
\frac{\partial l}{\partial z_4}
?z4??l?，再继续求
?
l
?
z
1
\frac{\partial l}{\partial z_1}
?z1??l?和
?
l
?
z
2
\frac{\partial l}{\partial z_2}
?z2??l?，最后我们就得到下图的结果 ：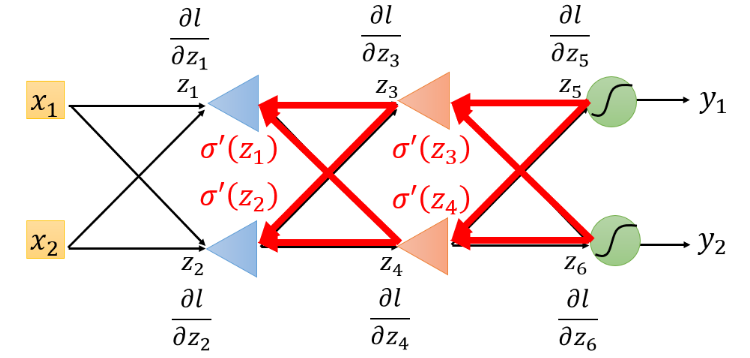
如此，实际上进行backward pass时候和向前传播的计算量差不多。