[人工智能]2021第一周周报

背景介绍

Reinforcement Learning (RL)

假设环境是一个有限长度的折扣马尔可夫决策过程，可以用一个七元组来表示 $\mathcal{M}=(\mathcal{S},\mathcal{A},\rho ,\mathcal{P},r,\gamma ，T)$，其中 $T$ 是决策过程总长度；$\mathcal{S}$ 是状态空间；$A$ 是行为空间；$r：\mathcal{S}\times \mathcal{A}?\mathbb{R}$ 是奖励函数用于衡量某个状态行为对 $(s,a),s\in \mathcal{S},a\in \mathcal{A}$ 的好坏；$\mathcal{P}:\mathcal{S}\times \mathcal{A}?[0,1]$ 表示环境的状态转移概率函数；$\rho :\mathcal{S}?[01]$ 表示环境的初始状态分布；$\gamma \in (0,1)$是折扣因子。

对于智能体的行为模式，用策略函数 $\pi :\mathcal{S}?\Delta (\mathcal{A})$ 表示，即条件分布 $\pi (a|s)$ 表示改智能体在状态 $s$ 处选择动作 $a$ 的概率。则该策略在 $\mathcal{M}$ 下的累计期望回报表示为值函数：
$$V(\pi )=\mathbb{E}\left[\sum _{t=0}^T{\gamma }^{t}r\left(s_t,a_t\right)\mid s_0～\rho (?),a_t～\pi \left(?\mid s_t\right),s_{t+1}～\mathcal{P}\left(s_{t+1}\mid s_t,a_t\right)\right]$$
对于强化学习问题，其目标是在 $r$ 已知的情况下求 ${\pi }^{?}\in \underset{\pi }{\mathrm{argmax}}V(\pi )$。

Imitation Learning (IL)

而在模仿学习中，$r$ 是未知或非常稀疏的，但有一个专家策略 ${\pi }^E$，假设专家策略是最优的，已知 ${\pi }^E$ 在 $\mathcal{M}$ 下产生了一系列交互数据 D E = { t r 1 , t r 2 , … ? } \mathcal{D}^E = \{tr_1,tr_2,\dots\} DE={tr1?,tr2?,…}，其中 t r = { ( s 1 , a 1 ) , ( s 2 , a 2 ) , ? ? , ( s T , a T ) } tr = \{(s_1,a_1),(s_2,a_2),\cdots,(s_T,a_T)\} tr={(s1?,a1?),(s2?,a2?),?,(sT?,aT?)} 表示智能体在环境中的一次完整轨迹。则模仿学习问题的目标是求 $\underset{\pi }{\mathrm{argmin}}V\left({\pi }^{\mathrm{E}}\right)?V(\pi )$。

为了反映状态行为对 $(s,a)$ 的访问频率，令策略 $\pi$ 对于状态 $s$ 和行为 $a$ 的状态动作访问分布表示为$d^{\pi }(s,a)=(1?\gamma ){\sum }_{t=0}^T{\gamma }^t{\mathbb{P}}^{\pi }\left(s_t=s,a_t=a\right)$，其中 ${\mathbb{P}}^{\pi }\left(s_t=s,a_t=a\right)$ 表示$t$ 时刻策略 $\pi$ 对状态行为对 $(s,a)$ 的访问概率。根据对偶分析，状态访问分布与值函数的联系为：
$$V(\pi )=\frac{1}{1?\gamma }\sum _{(s,a)\in \mathcal{S}\times \mathcal{A}}{d}^{\pi }(s,a)r(s,a)$$
则当策略 $\pi$ 的状态动作分布 $d^{\pi }$ 和专家策略的状态动作分布 $d^{{\pi }^E}$ 距离很小时，$V\left({\pi }^{\mathrm{E}}\right)?V(\pi )$ 也会很小，因此生成对抗式模仿学习试图通过最小化状态动作分布来求出专家策略：

$$\underset{\pi \in \Pi }{\min }\psi \left(d^{\pi },d^{{\pi }^{\mathrm{E}}}\right)$$

其中 $\psi$ 是距离度量函数。

Generative Adversarial Imitation Learning (GAIL)

在生成对抗式模仿学习算法中，使用Jesen-Shannon距离进行度量，即：
$$\underset{\pi \in \Pi }{\min }{D}_{\mathrm{J}\mathrm{S}}\left(d^{\pi },d^{{\pi }^{\mathrm{E}}}\right)$$
其中 ${\hat{h}}^{{\pi }^E}$ 是专家的状态动作分布估计器，则该算法的目标与GAN类似：
$$\underset{\pi \in \Pi }{\min }\underset{D:\mathcal{S}\times \mathcal{A}\to \mathbb{R}}{\max }{\mathbb{E}}_{(s,a)～d^{\pi }\mathrm{E}}[\log (D(s,a))]+{\mathbb{E}}_{(s,a)～d^{\pi }}[\log (1?D(s,a))]$$
其中 $D$ 是判别器，用于区分某个状态动作对 $(s,a)$ 是由专家策略 ${\pi }^E$ 还是模仿策略 $\pi$ 产生，使用 Adam算法进行优化。

$\pi$ 是生成器，目标是产生与专家数据相似度状态行为对，混淆判别器，使用 TRPO 等强化学习算法进行优化。

最后，根据因果熵理论，GAIL 使用 $\lambda H(\pi )={\mathbb{E}}_{\pi }[?\log \pi (s|a)]$ 作为正则化项对策略进行限制，使得到的策略唯一：
$$\underset{\pi \in \Pi }{\min }\underset{D:\mathcal{S}\times \mathcal{A}\to \mathbb{R}}{\max }\left({\mathbb{E}}_{(s,a)～d^{\pi }\mathrm{E}}[\log (D(s,a))]+{\mathbb{E}}_{(s,a)～d^{\pi }}[\log (1?D(s,a))]\right)?\lambda H(\pi )$$

Model-Agnostic Meta-Learning (MAML)

元学习上一种利用任务结构的相似性，使学习模型快速适应新环境的方法。与模型无关的元学习框架（MAML）通过二次梯度下降来获得一个较好的模型初始参数。具体来说是先让模型在多个子任务上进行梯度下降，然后利用这些梯度信息对原模型进行梯度下降。

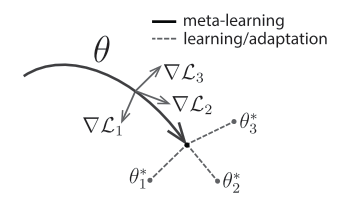
问题与方案

对于黑白棋问题，我们有 $m$ 个各不同级别风格的玩家数据，即 D = { D E i } i = 1 m \mathcal{D} = \{\mathcal{D}^{E_i}\}_{i=1}^m D={DEi?}i=1m?，目的是求每个玩家在黑白棋环境下的累计期望回报 { V ( π E i ) } i = 1 m \{V(\pi^{E_i})\}_{i=1}^m {V(πEi?)}i=1m?。由于环境相同，因此假设每个玩家基本策略具有相似性，同时拥有相似的状态访问概率。

在元学习的框架下使用生成对抗模仿学习算法学习各个玩家的策略，先在多个 ${\mathcal{D}}^{E_i}$ 上使用 GAIL ，通过自博弈的方式采样数据，并获得策略 ${\pi }^{E_i}$ 的策略梯度和鉴别器 $D_i$ 的梯度，利用这些梯度信息更新元模型的策略 ${\pi }^{meta}$ 和鉴别器 $D^{meta}$ 的梯度。训练完成后 ${\pi }^{meta}$ 只需要少量数据即可学习到 ${\pi }^{E_i}$。