1.算法简介
1. 𝑘 近邻法是基本且简单的分类与回归方法。 𝑘 近邻法的基本做法是:对给定的训练实例点和输入实例点,首先确定输入实例点的 𝑘 个最近邻训练实例点,然后利用这 𝑘 个训练实例点的类的多数来预测输入实例点的类。
2. 𝑘 近邻模型对应于基于训练数据集对特征空间的一个划分。 𝑘 近邻法中,当训练集、距离度量、 𝑘 值及分类决策规则确定后,其结果唯一确定。
3. 𝑘 近邻法三要素:距离度量、 𝑘 值的选择和分类决策规则。常用的距离度量是欧氏距离及更一般的pL距离。 𝑘 值小时, 𝑘 近邻模型更复杂; 𝑘 值大时, 𝑘 近邻模型更简单。 𝑘 值的选择反映了对近似误差与估计误差之间的权衡,通常由交叉验证选择最优的 𝑘 。
常用的分类决策规则是多数表决,对应于经验风险最小化。
4. 𝑘 近邻法的实现需要考虑如何快速搜索k个最近邻点,并用分类决策规则确定最终点的归类。
距离度量
设特征空间
x
x
x是
n
n
n维实数向量空间 ,
x
i
,
x
j
∈
X
x_{i}, x_{j} \in \mathcal{X}
xi?,xj?∈X,
x
i
=
(
x
i
(
1
)
,
x
i
(
2
)
,
?
?
,
x
i
(
n
)
)
T
x_{i}=\left(x_{i}^{(1)}, x_{i}^{(2)}, \cdots, x_{i}^{(n)}\right)^{\mathrm{T}}
xi?=(xi(1)?,xi(2)?,?,xi(n)?)T,
x
j
=
(
x
j
(
1
)
,
x
j
(
2
)
,
?
?
,
x
j
(
n
)
)
T
x_{j}=\left(x_{j}^{(1)}, x_{j}^{(2)}, \cdots, x_{j}^{(n)}\right)^{\mathrm{T}}
xj?=(xj(1)?,xj(2)?,?,xj(n)?)T
,则:
x
i
x_i
xi?,
x
j
x_j
xj?的
L
p
L_p
Lp?距离定义为:
L p ( x i , x j ) = ( ∑ i = 1 n ∣ x i ( i ) ? x j ( l ) ∣ p ) 1 p L_{p}\left(x_{i}, x_{j}\right)=\left(\sum_{i=1}^{n}\left|x_{i}^{(i)}-x_{j}^{(l)}\right|^{p}\right)^{\frac{1}{p}} Lp?(xi?,xj?)=(∑i=1n?∣∣∣?xi(i)??xj(l)?∣∣∣?p)p1?
- p = 1 p= 1 p=1 曼哈顿距离
- p = 2 p= 2 p=2 欧氏距离
- p = ∞ p= \infty p=∞ 切比雪夫距离
算法图示
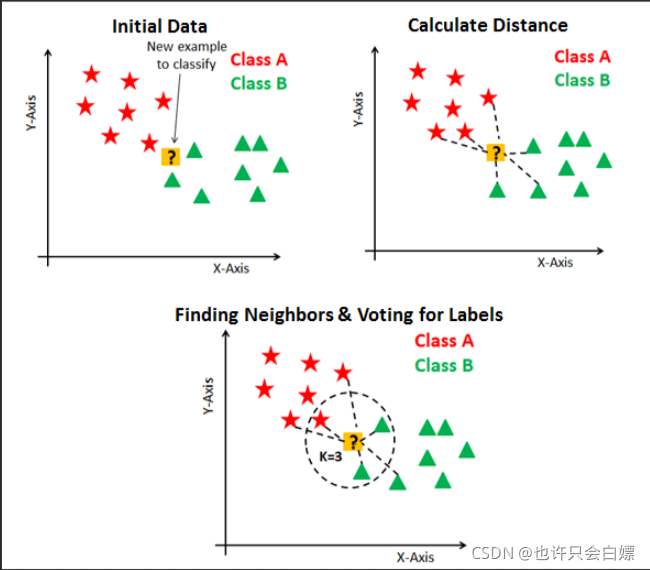
2.算法流程
(1)收集数据:使用数据集使用sklearn下自带的手写数字数据集:load_digits
(2)准备数据:使用sklearn中的train_test_split()方法
(3)分析数据:并未进行
(4)训练算法:无可训练的参数
(5)测试算法:用sklearn数据集的一部分进行测试
其中对未知类别属性的数据集中的每个点依次执行一下操作:
(1)计算已知类别数据集中的点与当前点之间的距离;
(2)按照距离递增次序排序;
(3)选取与当前点距离最近的k个点;
(4)确定前k个点所在类别的出现频率;
(5)返回前k个点出现频率最高的类别作为当前点的预测分类。
3.代码部分
1.数据集(借某天的代码doge)
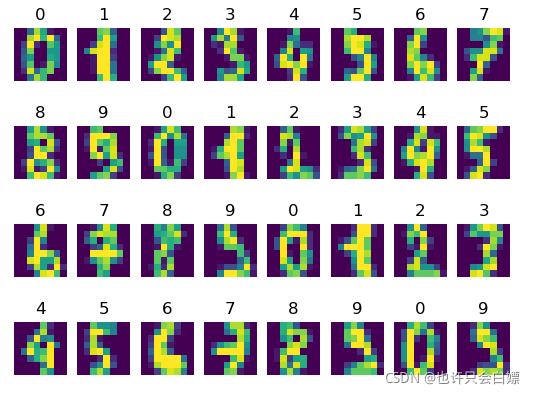
import matplotlib.pyplot as plt
import sklearn.datasets as datasets # 数据集模块
# 读取数据集
X, y = datasets.load_digits(return_X_y=True)
for i in range(32):
plt.subplot(4, 8, i + 1)
img = X[i, :].reshape(8, 8)
plt.imshow(img)
plt.title(y[i])
plt.axis("off")
plt.subplots_adjust(hspace=0.3) # 微调行间距
plt.show()
2.KNN类 knn.py
import operator
import numpy as np
class KNN:
def __init__(self, X_test, X_train, y_train, k=3, p=2):
"""
parameter: k 临近点个数
parameter: p 距离度量
"""
self.k = k
self.p = p
self.X_train = X_train
self.y_train = y_train
self.X_test = X_test
def distance(self, x, y):
"""
:param x: 单个测试样本
:param y: 训练集X_train
:return: 单个样本到训练集上各点的距离
"""
X_trainSize = self.X_train.shape[0] # 获得第一个维度的长度
# 将x重复dataSetSize次使其shape和X_train一样
x = np.tile(x, (X_trainSize, 1))
if len(x) == len(y) and len(x) > 1:
sum = np.zeros((len(x)))
# 计算距离,p=2为欧式距离
for i in range(len(x)):
sum[i] = np.sum(np.power(x[i] - y[i], self.p))
sum = np.power(sum, 1 / self.p)
# print(sum)
return sum
else:
print("illegal data!")
def predictData(self, inX): # inX 为单个测试数据
distances = self.distance(inX, self.X_train)
# argsort函数返回的是distances值从小到大的--索引值
sortedDistIndicies = distances.argsort()
# 定义一个记录类别次数的字典
classCount = {}
# 选择距离最小的k个点
for i in range(self.k):
# 取出前k个元素的类别
voteIlabel = self.y_train[sortedDistIndicies[i]]
# 字典的get()方法,返回指定键的值,如果值不在字典中返回0
# 计算类别次数
classCount[voteIlabel] = classCount.get(voteIlabel, 0) + 1
# python3中用items()替换python2中的iteritems()
# key = operator.itemgetter(1)根据字典的值进行排序
# key = operator.itemgetter(0)根据字典的键进行排序
# reverse降序排序字典
sortedClassCount = sorted(classCount.items(),
key=operator.itemgetter(1), reverse=True)
# 返回次数最多的类别,即所要分类的类别
return sortedClassCount[0][0]
def kNN(self):
predict = []
for i in range(self.X_test.shape[0]):
predict.append(self.predictData(self.X_test[i]))
return np.array(predict)
3.加入数据实践
import numpy as np
import sklearn.datasets as datasets # 数据集模块
from sklearn.model_selection import train_test_split # 划分训练集和验证集
import time
# 读取数据集
from ML_STUDY.KNN.knn import KNN # 看个人的项目路径
X, y = datasets.load_digits(return_X_y=True)
# 随机划分训练集和验证集,使用sklearn中的方法
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
# KNN最近邻进行分类(k默认为3)
knn = KNN(X_test, X_train, y_train) # 后面依次缺省了,k=3,p=2(欧式距离)
# 获取程序运行时间
start = time.process_time() # 打开文件的名称Python 3.8 已移除 clock() 方法 可以使用 time.perf_counter() 或 time.process_time() 方法替
pred = knn.kNN()
end = time.process_time()
# 打印程序运行时间
print('Running time: %f Seconds' % (end - start))
# 分类准确率
accuracy = np.mean(pred == y_test)
print('准确率:', accuracy)
4.运行结果
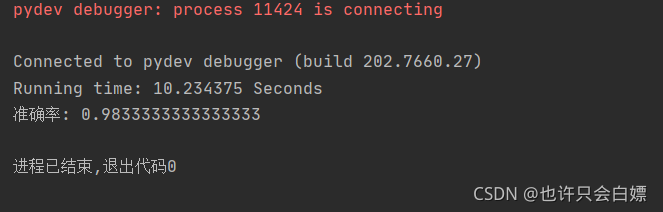
5.结果分析
knn算法并没有用于训练的参数,其中有两个超参数值得注意,一个是选取的临近点个数k,一个是距离度量方式p(可看上方距离度量了解)关于什么选值效果最好博主不打算继续演示doge。