代价函数
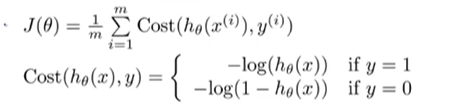
将cost分段函数整合成一个函数:
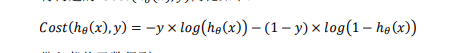
即y=1时cost=?𝑙𝑜𝑔(?𝜃(𝑥)),y=0时cost=?𝑙𝑜𝑔(1 ? ?𝜃(𝑥))。
代入代价函数得:
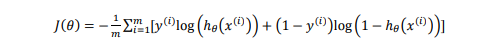
梯度下降法
在得到这样一个代价函数以后,我们便可以用梯度下降算法来求得能使代价函数最小的参数了。
梯度函数原式:
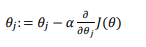
其中: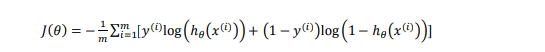
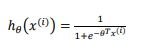
将h代入代入J函数得: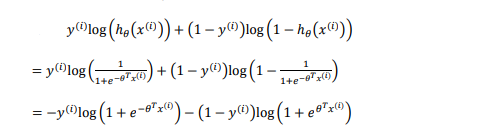
在将得到得J函数代入梯度下降函数得:
虽然得到的梯度下降算法表面上看上去与线性回归的梯度下降算法一样,但是这里的?𝜃(𝑥) = 𝑔(𝜃𝑇𝑋)与线性回归中不同,所以实际上是不一样的。
一些梯度下降算法之外的选择: 除了梯度下降算法以外,还有一些常被用来令代价函数最小的算法,比梯度下降算法要更加快速。这些算法有:共轭梯度(Conjugate Gradient),局部优化法(Broyden fletcher goldfarb shann,BFGS)和有限内存局部优化法(LBFGS) 。
一对多的分类算法
多是指分类的类别数量。
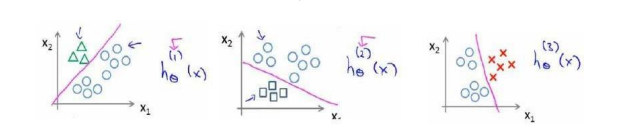
每次训练一个逻辑回归分类器:每个分类器都是只针对其中一种分类情况进行训练。
总结:?𝜃(𝑖)(𝑥),其中 𝑖 对应每一个可能的 𝑦 = 𝑖,最后,为了做出预测,我们给出输入一个新的 𝑥值,用这个做预测。我们要做的就是在我们三个分类器里面输入 𝑥,然后我们选择一让 ?𝜃(𝑖)(𝑥)最大的𝑖,即max𝑖?𝜃(𝑖)(𝑥)。