一、概述
基于AI的量化投资领域特别是针对A股市场的AI技术已经成为了当下的热点话题,本文将基于big quant平台,了解并掌握量化投资的一些基本操作方法,并通过一些QP优化策略实现选股。
二、基于技术指标的策略
2.1 策略1:技术指标MACD金叉 + MA多头
在本章中,我们将基于技术指标策略进行选股操作。在股市交易市场中,人们会采取一定的技术指标建立相应的数学模型进行股票分析,如MACD、DMI、KDJ等等。在策略1中,我们将采取MACD金叉+MA多头的策略进行选股。MACD金叉指的是将DIF线上穿DEA线作为买入信号,指多头排列短线在长线上方,预示市场趋势是强势上升势。
在建立策略前,我们需要为策略提供初始化环境。
- 股票池:在本项目中,采取已经给好的stock_list.txt中的股票池
- 回测时间:2019年1月3日-2021年1月22日
- 交易费用:按0.3%收取,小于5元部分收取5元
- 资金总额:1000000
- 调仓周期:20天
- 允许最大持股:10
- 每种股票的持股比例:平均
- ?基准:沪深300
首先是股票池的选择,对于给定好的股票池列表,其中包含重复数据和已退市股票,我们还需要进一步对数据进行筛选。代码如下:
from collection import Counter
#获取数据
start_date = '2019-01-03'
end_date = '2021-01-22'
instruments = stock_list
# 数据预处理,由于存在重复股票代码以及已经退市的股票代码,会对后续优化矩阵造成影响
## 重复数据剔除
repeated_ins = dict(Counter(instruments))
repeat = [key for key,value in repeated_ins.items() if value > 1]
drop_index = []
for i in range(len(repeat)):
drop_index.append(instruments.index(repeat[i]))
## 股票过滤,剔除已经退市的股票
df = D.history_data(instruments,start_date,end_date,fields=['close','st_status'])
ins = list(set(df[df['instrument'] != 0].instrument))
st_ins = list(set(df[df['st_status'] != 0].instrument))
drop_ins = [i for i in instruments if i not in ins]
drop_ins.extend(st_ins)
for idx, instrument in enumerate(instruments):
if instrument in drop_ins:
drop_index.append(idx)
else:
continue
## 重新建立instruments
all_ins = [instruments[i] for i in range(len(instruments)) if i not in drop_index]在big quant中,实现技术指标选股,可以通过特征筛选模快来执行,如本策略中的技术指标可以通过如下代码实现:
m2 = M.input_features.v1(
features="""
# #号开始的表示注释,注释需单独一行
# 多个特征,每行一个,可以包含基础特征和衍生特征,特征须为本平台特征
# 选股条件
cond=(ta_ma(close_0/adjust_factor_0, shorttimeperiod=5, longtimeperiod=20, derive='long'))&\
(ta_macd(close_0/adjust_factor_0, fastperiod=12, slowperiod=9, signalperiod=26, derive='golden_cross'))
"""
)在执行回测模块时,可以通过对特征值筛选选出每天符合技术指标的股票。回测模快如下:
# 回测引擎:初始化函数,只执行一次
def m7_initialize_bigquant_run(context):
# 加载计算数据
df = context.options['data'].read_df()
# 函数:计算满足买入条件的股票列表
def today_enter_stock(df):
return list(df[df['cond']>0].instrument)
# 逐日计算买入列表
context.enter_daily_df = df.groupby('date').apply(today_enter_stock)
# 系统已经设置了默认的交易手续费和滑点,要修改手续费可使用如下函数
context.set_commission(PerOrder(buy_cost=0.003, sell_cost=0.003, min_cost=5))
# 设置买入的股票数量,这里买入预测股票列表排名靠前的10只
context.max_stock_count = 10
# 设置每只股票占用的最大资金比例
context.max_cash_per_instrument = 1
context.hold_days = 20
# 回测引擎:每日数据处理函数,每天执行一次
def m7_handle_data_bigquant_run(context, data):
# 获取今日的日期字符串
date = data.current_dt.strftime('%Y-%m-%d')
# 当日符合条件买入的股票
try:
today_enter_stock = context.enter_daily_df[date]
except KeyError as e:
today_enter_stock = []
# 当前持仓股票
stock_hold_now = [equity.symbol for equity in context.portfolio.positions]
# 确定股票权重
if len(today_enter_stock) < context.max_stock_count and len(today_enter_stock) != 0:
equal_weight = 1/len(today_enter_stock)
else:
equal_weight = 1/context.max_stock_count
#--------------------卖出-------------------#
if (context.trading_day_index + 1) % context.hold_days == 0:
for stock in stock_hold_now:
context.order_target_percent(context.symbol(stock), 0)
#--------------------买入-------------------#
if (context.trading_day_index) % context.hold_days == 0:
if len(today_enter_stock) < context.max_stock_count and len(today_enter_stock) != 0:
for stock in today_enter_stock:
context.order_target_percent(context.symbol(stock), equal_weight)
else:
today_buy_count = 0
for stock in today_enter_stock:
if today_buy_count >= context.max_stock_count:
break
else:
context.order_target_percent(context.symbol(stock), equal_weight)
today_buy_count += 1
m7 = M.trade.v4(
instruments=m1.data,
options_data=m5.data,
start_date='',
end_date='',
initialize=m7_initialize_bigquant_run,
handle_data=m7_handle_data_bigquant_run,
prepare=m7_prepare_bigquant_run,
before_trading_start=m7_before_trading_start_bigquant_run,
volume_limit=0.025,
order_price_field_buy='open',
order_price_field_sell='close',
capital_base=1000000,
auto_cancel_non_tradable_orders=True,
data_frequency='daily',
price_type='真实价格',
product_type='股票',
plot_charts=True,
backtest_only=False,
benchmark=''
)?回测结果如下:
 ?我们可以看到股票的收益情况在20年的收益情况较好,19年几乎没有什么收益。同时最大回撤达到了24.11%,说明风险较高。
?我们可以看到股票的收益情况在20年的收益情况较好,19年几乎没有什么收益。同时最大回撤达到了24.11%,说明风险较高。
2.2 策略2:KDJ金叉
在策略2中,我们采取KDJ金叉作为买入信号,KDJ金叉指的是K线上穿D线并形成有效的向上突破。同时我们调整了一些初始化环境:
- 股票池、回测时间、交易费用、资金总额、基准同上
- 调仓周期:40天
- 允许最大持股:5
- 每种股票的持有比例:平均
更改策略后的代码如下:
m2 = M.input_features.v1(
features="""
# #号开始的表示注释,注释需单独一行
# 多个特征,每行一个,可以包含基础特征和衍生特征,特征须为本平台特征
# 选股条件
cond=(ta_kdj(high_0/adjust_factor_0, low_0/adjust_factor_0, close_0/adjust_factor_0, N=9, M1=3, M2=3, derive='golden_cross'))"""
)回测结果:
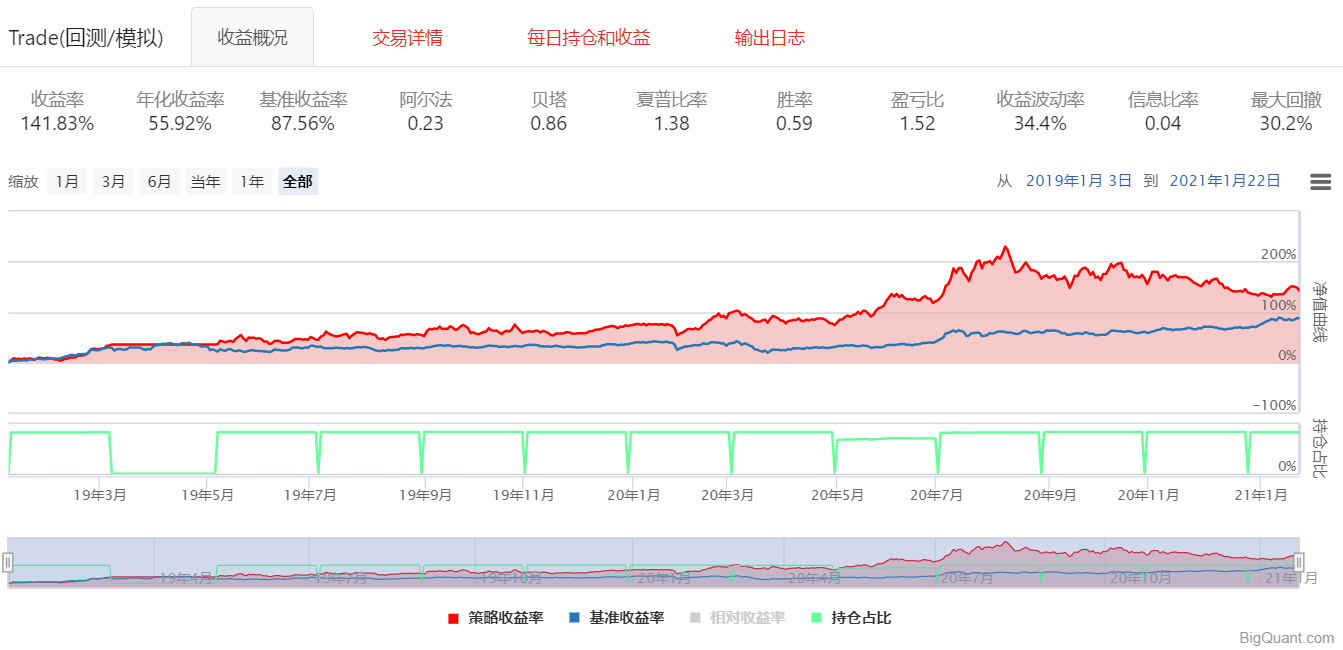
?我们可以看到,整体的收益情况是要优于之前的策略的,但风险也变大了。
三、基于QP的策略
3.1 策略3:经典的QP优化
基于QP的优化问题是通过计算过去一段历史时间的收益及风险来确定选股策略。假设我们定义每支股票的权重向量为,满足
,其中n代表股票池的大小。这些股票表现出的历史期望为
,这里按照5个工作日来计算。
代表收益的协方差矩阵,代表着股票之间的关系。因此经典QP问题可表述为:
在本策略中,采取的初始化环境为:
- 股票池、回测时间、交易费用、资金总额、基准同上
- 调仓周期:10天
- 不再设置最大持股数和持股比例,该项由QP优化的结果决定
该部分的实现代码如下:
def optimal_QP(returns):
returns = np.asmatrix(returns)
mu = returns.mean(axis=1)
sigma = np.cov(returns)
n = len(returns)
# 转化为cvxopt matrices
P = opt.matrix(sigma)
q = -opt.matrix(mu)
A = opt.matrix(1.0, (1, n))
b = opt.matrix(1.0)
G = -opt.matrix(np.eye(n))
h = opt.matrix(0.0, (n ,1))
# 设置hyperparameter lambda=1
# 计算最优组合
wt = solvers.qp(P, -q, G, h, A, b)['x']
return np.asarray(wt)
def initialize(context):
context.set_commission(PerOrder(buy_cost=0.003, sell_cost=0.003, min_cost=5))
context.trading_days = 10
context.calculate_days = 5
def handle_data(context, data):
if context.trading_day_index < context.calculate_days:
return
# 每10天调仓一次
if context.trading_day_index % context.trading_days != 0:
return
# 获取数据的时间窗口并计算收益率
sid = context.symbols(*all_ins)
prices = data.history(sid, 'price', 6, '1d') # 我们需要计算5个工作日的收益率,所以需要获取6天的历史价格
returns_ = prices.pct_change().dropna()
try:
weights = optimal_QP(returns_.T)
# print(weights)
# 对持仓进行权重调整
for stock, weight in zip(prices.columns, weights):
if data.can_trade(stock):
order_target_percent(stock, weight[0])
except ValueError as e:
pass
m=M.trade.v2(
instruments=instruments,
start_date=start_date,
end_date=end_date,
initialize=initialize,
handle_data=handle_data,
order_price_field_buy='open',
order_price_field_sell='close',
capital_base=1000000,
benchmark='000300.SHA',
)?回测结果如下:
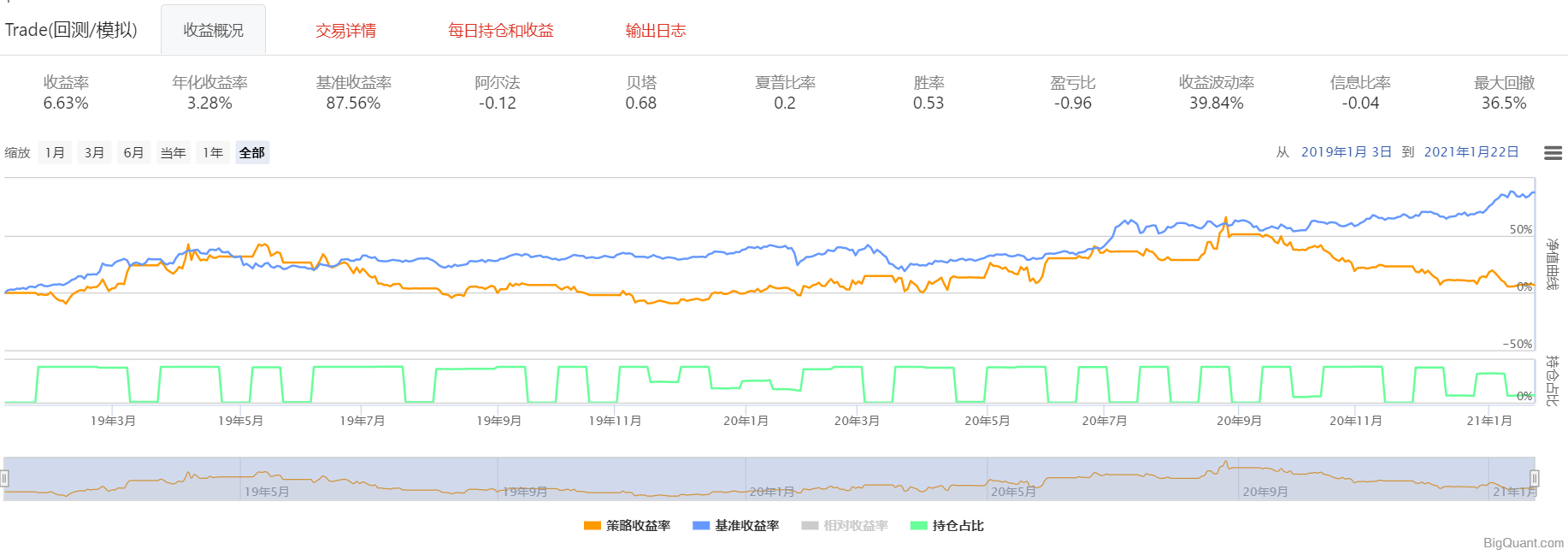
通过回测结果,我们可以看出QP策略保持了略微的受益率,但并没有跑赢大盘,因此这种策略并不是很好。
3.2 策略4:让选中的股票具有多样性
在策略3中得到结果我们可以发现,交易过程中并没有购入多只股票,而是以一两只股票为主进行交易,这是因为优化结果中有些股票的权重特别高,有些股票的权重几乎可以忽略不计。因此我们需要通过改进策略进行选股。这里考虑两个方面:1. 限制单个股票的权重上限,2. 限制某个行业股票的权重上限。因此我们在优化公式的约束部分进行了调整:
这里我们限制单只股票的权重不超过10%,每一个行业的股票权重不超过30%。
在执行代码前,我们需要对数据按照行业进行分类处理。代码如下:
from collection import Counter
#获取数据
start_date = '2019-01-03'
end_date = '2021-01-22'
instruments = stock_list
# 数据预处理,由于存在重复股票代码以及已经退市的股票代码,会对后续优化矩阵造成影响
## 重复数据剔除
repeated_ins = dict(Counter(instruments))
repeat = [key for key,value in repeated_ins.items() if value > 1]
drop_index = []
for i in range(len(repeat)):
drop_index.append(instruments.index(repeat[i]))
## 股票过滤,剔除已经退市的股票
df = D.history_data(instruments,start_date,end_date,fields=['close','st_status'])
ins = list(set(df[df['instrument'] != 0].instrument))
st_ins = list(set(df[df['st_status'] != 0].instrument))
drop_ins = [i for i in instruments if i not in ins]
drop_ins.extend(st_ins)
for idx, instrument in enumerate(instruments):
if instrument in drop_ins:
drop_index.append(idx)
else:
continue
## 重新建立instruments
all_ins = [instruments[i] for i in range(len(instruments)) if i not in drop_index]
## 建立行业分类列表,已知在instruments中,每10个为同一行业,一共12个行业
industry_classes = []
for i in range(12):
industry_class = [i for q in range(10)]
industry_classes.extend(industry_class)
industry_classes = [industry_classes[i] for i in range(len(industry_classes)) if i not in drop_index]QP部分代码修订为:
def optimal_QP(returns):
returns = np.asmatrix(returns)
mu = returns.mean(axis=1)
sigma = np.cov(returns)
n = len(returns)
# G矩阵
## 限制每一支股票的权重不超过30%
m = 0.3
G1 = np.eye(n)
h1 = m * np.ones([n, 1])
## 限制单个行业的股票权重总和不超过50%
mk = 0.5
classes = np.array(industry_classes)
G2 = np.zeros([12, len(industry_classes)])
for i in range(12):
G2[i] = (classes==i)
h2 = mk * np.ones([12, 1])
## 每一支股票的权重至少为0
G3 = -np.eye(n)
h3 = np.zeros([n, 1])
G = np.vstack((G1, G2, G3))
h = np.vstack((h1, h2, h3))
# 转化为cvxopt matrices
P = opt.matrix(sigma)
q = -opt.matrix(mu)
A = opt.matrix(1.0, (1, n))
b = opt.matrix(1.0)
G = opt.matrix(G)
h = opt.matrix(h)
# 设置hyperparameter lambda=1
# 计算最优组合
wt = solvers.qp(P, -q, G, h, A, b)['x']
return np.asarray(wt)?回测结果如下:
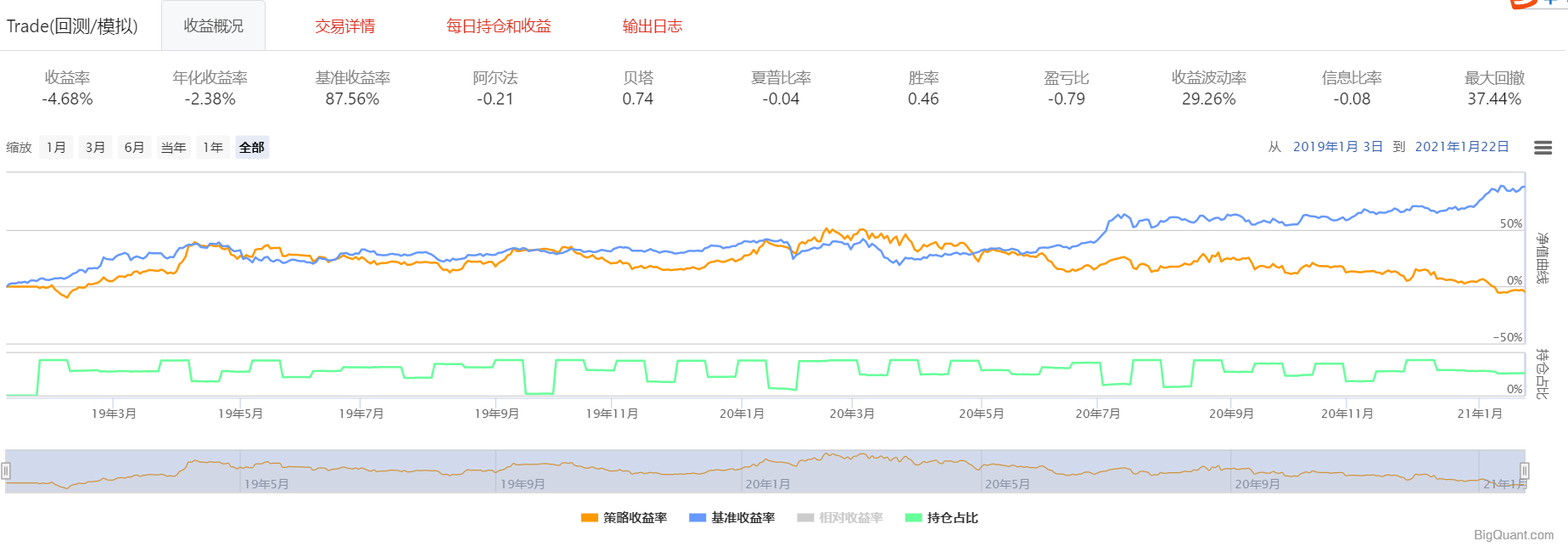
?
在考虑选股多样性后,尽管受益情况没有多少改善,但我们观察持仓情况,发现持有股票具有了多样性。?
3.3 考虑手续费
频繁的买卖操作会增加手续费占比,从而导致收益变差,因此我们需要在调仓时设置调仓额度,首先我们希望对单只股票的调仓值做出限制,同时我们也希望对调仓总和
作出限制。那么优化问题如下:
在实际优化中,我们需要对目标函数和约束进行更改,这里认为优化问题中yi和zi也是变量,则目标函数中的变量需要改为,一阶优化项一次项
,二次项矩阵
,约束部分也需要进行相同的改进。
根据优化问题的描述,我们构造的不等式约束应该是10个,等式约束1个,我们通过array的拼接来实现G矩阵的构造。因此,QP优化部分的代码如下:
def optimal_QP(returns, weights):
returns = np.asmatrix(returns)
mu = returns.mean(axis=1)
sigma = np.cov(returns)
n = len(returns)
# 不等式约束
## 限制每一支股票的权重不超过30%
m = 0.3
G1_x = np.eye(n)
G1_y = np.zeros_like(G1_x)
G1_z = np.zeros_like(G1_x)
G1 = np.hstack((G1_x, G1_y, G1_z))
h1 = m * np.ones([n, 1])
## 限制单个行业的股票权重总和不超过50%
mk = 0.5
classes = np.array(industry_classes)
G2_x = np.zeros([12, len(industry_classes)])
for i in range(12):
G2_x[i] = (classes==i)
G2_y = np.zeros_like(G2_x)
G2_z = np.zeros_like(G2_x)
G2 = np.hstack((G2_x, G2_y, G2_z))
h2 = mk * np.ones([12, 1])
## 每一支股票的权重至少为0
G3_x = -np.eye(n)
G3_y = np.zeros_like(G3_x)
G3_z = np.zeros_like(G3_x)
G3 = np.hstack((G3_x, G3_y, G3_z))
h3 = np.zeros([n, 1])
## 限制单个股票的调仓值不超过10%
G4_x = np.eye(n)
G4_y = -np.eye(n)
G4_z = np.zeros_like(G4_x)
G4 = np.hstack((G4_x, G4_y, G4_z))
G5_x = -np.eye(n)
G5_y = np.zeros_like(G5_x)
G5_z = -np.eye(n)
G5 = np.hstack((G5_x, G5_y, G5_z))
h4 = weights
h5 = -weights
G6 = np.hstack((G1_y, G1_x, G1_z))
h6 = 0.1 * np.ones([n, 1])
G7 = -G6
h7 = np.zeros([n, 1])
G8 = np.hstack((G1_y, G1_z, G1_x))
h8 = 0.1 * np.ones([n, 1])
G9 = -G8
h9 = np.zeros([n, 1])
## 限制调仓上限50%
G10_y = np.ones([1, n])
G10_z = np.ones([1, n])
G10_x = np.zeros([1, n])
h10 = np.array([0.5])
G10 = np.hstack((G10_x, G10_y, G10_z))
G = np.vstack((G1, G2, G3, G4, G5, G6, G7, G8, G9, G10))
h = np.vstack((h1, h2, h3, h4, h5, h6, h7, h8, h9, h10))
# 等式约束
A_x = np.ones([1, n])
A_y = np.zeros_like(A_x)
A_z = np.zeros_like(A_x)
A = np.hstack((A_x, A_y, A_z))
# 目标函数
P_x = sigma
P = np.zeros([3*n, 3*n])
P[0:n, 0:n] = sigma
q = np.zeros([3*n, 1])
q[0:n] = -mu
# 转化为cvxopt matrices
P = opt.matrix(P)
q = opt.matrix(q)
A = opt.matrix(A)
b = opt.matrix(1.0)
G = opt.matrix(G)
h = opt.matrix(h)
# 设置hyperparameter lambda=1/2
# 计算最优组合
wt = solvers.qp(P, -q, G, h, A, b)['x']
weight_for_stock = wt[0:n]
return np.asarray(weight_for_stock)这里要注意的是,首次执行时由于不存在上一次权重数据,所以仍然需要依靠策略4中的代码进行启动。
得到的回测结果如下图:
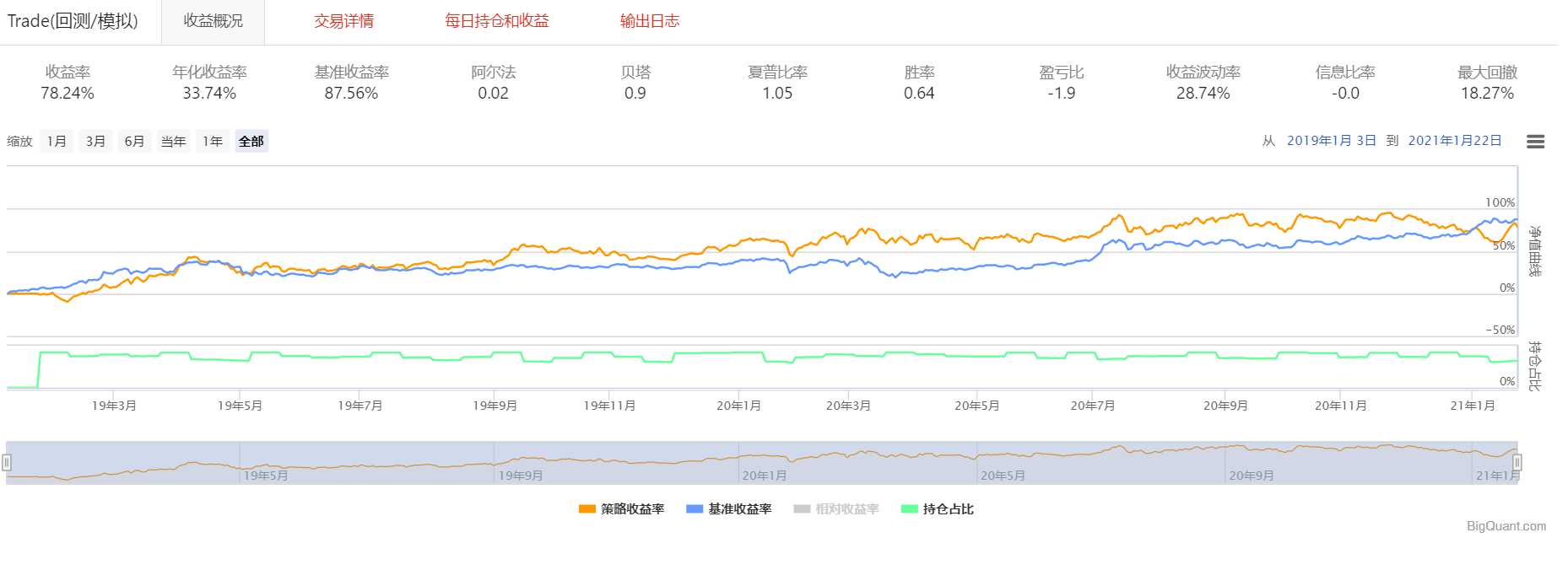
我们可以看出该策略执行后的结果有了较好的改善,执行策略受益情况基本与大盘持平,同时最大回撤也有所降低。我们观察了一下具体的交易情况,发现该种策略的手续费额基本控制在2000~3500元之间。而策略4的手续费达到了4000以上。但相较于策略4,计算代价同样增加了许多。
四、总结
本次项目通过技术指标以及机器学习两种方式进行了选股操作,对比两种手段我们可以更好地区分机器学习任务与传统的数学建模任务之间的差别。在QP优化部分,我们通过一步步增加约束来改进模型,执行代码,并观测回测结果,使我们对机器学习任务的模型构建有了更深入地了解。