卷积
操作
略
输入输出尺寸变化
略
PyTorch实现
nn.Conv2d(in_channels,
out_channels,
kernel_size,
stride=1.
padding=0,
dilation=1,
groups=1,
bias=True,
padding_mode='zeros')
in_channels:输入通道数
out_channels:输出通道数,等价于卷积核个数
kernel_size:卷积核尺寸
stride:步长
padding:填充个数
dilation:空洞卷积大小
groups:分组卷积设置
bias:偏置,在卷积求和之后加上偏置的值
conv_layer = nn.Conv2d(3, 1, 3) # input:(i, o, size) weights:(o, i , h, w),输入为三个通道,卷积核个数1个,输出通道为1
nn.init.xavier_normal_(conv_layer.weight.data) # 卷积层初始化
# calculation
img_conv = conv_layer(img_tensor) # 图片进入卷积层
转置卷积
主要参考为知乎文章:
一问搞懂反卷积、转置卷积
总结如下:
当我们用神经网络生成图片的时候,经常需要将一些低分辨率的图片转换为高分辨率的图片,目前有着一些插值方法进行处理:
- 最近邻插值(Nearest neighbor interpolation)
- 双线性插值(Bi-Linear interpolation)
- 双立方插值(Bi-Cubic interpolation)
以上的这些方法都是一些插值方法,需要我们在决定网络结构的时候进行挑选。这些方法就像是人工特征工程一样,并没有给神经网络学习的余地,神经网络不能自己学习如何更好地进行插值,这个显然是不够理想的。
如果我们想要我们的网络可以学习到最好地上采样的方法,我们这个时候就可以采用转置卷积。这个方法不会使用预先定义的插值方法,它具有可以学习的参数。
关于名称
转置卷积**(Transposed Convolution)常常在一些文献中也称之为反卷积(Deconvolution)和部分跨越卷积(Fractionally-strided Convolution)**,因为称之为反卷积容易让人以为和数字信号处理中反卷积混起来,造成不必要的误解,因此下文都将称为转置卷积,并且建议各位不要采用反卷积这个称呼。
具体操作
首先对于卷积操作,以输入4x4,卷积核3x3,输出为2x2为例

一个卷积操作是一个多对一(many-to-one)的映射关系
转置卷积的核心是维护一个一对多(one-to-many)的映射关系。每一个“对”实际上都需要维护一组权值。
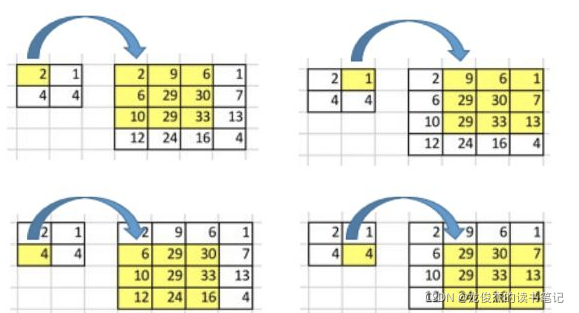
需要注意的是:这里的转置卷积矩阵的参数,不一定从原始的卷积矩阵中简单转置得到的,转置这个操作只是提供了转置卷积矩阵的形状而已
总结
- 转置卷积操作构建了和普通的卷积操作一样的连接关系,只不过这个是从反向方向开始连接的,我们可以用它进行上采样。
- 转置卷积矩阵的参数是可以学习的,因此我们不需要一些人为预先定义的方法。 并不是意味着我们将一些现存的卷积矩阵简单转置并且使用其转置后的值。
- 转置卷积会导致生成图像中出现棋盘效应(checkerboard artifacts),这篇文章《Deconvolution and Checkerboard Artifacts》推荐了一种上采样的操作(也就是插值操作),这个操作接在一个卷积操作后面以减少这种现象。如果你的主要目的是生成尽可能少棋盘效应的图像,那么这篇文章就值得你去阅读。
- Q:转置卷积矩阵的参数随着训练过程不断被优化,但是它是在随机初始化的基础上进行优化,还是在原始卷积矩阵的基础上进行优化;A:一般地进行随机初始化即可
-
PyTorch实现
nn.ConvTranspose2d
nn.ConvTranspose2d(in_channels,
out_channels,
kernel_size,
stride=1,
padding=0,
output_padding=0,
groups=1,
bias=True,
dilation=1,
padding_mode='zores')
- in_channels:输入通道数
- out_channels:输出通道数
- kernel_size:卷积核尺寸
- stride:步长
- padding:填充个数
- dilation:空洞卷积大小
- groups:分组卷积设置
- bias:偏置
转置卷积的使用:
conv_layer = nn.ConvTranspose2d(3, 1, 3, stride=2) # input:(i, o, size)
nn.init.xavier_normal_(conv_layer.weight.data)
# calculation
img_conv = conv_layer(img_tensor)
效果:
