开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 人工智能 -> 【生成模型】变分自编码器（VAE）及图变分自编码器（VGAE） -> 正文阅读

[人工智能]【生成模型】变分自编码器（VAE）及图变分自编码器（VGAE）

这段时间在学习机器学习中有关不确定性和概率分布的知识，发现了VAE这样一个有趣的方向，想抓紧时间整理一下VAE的主要思想和方法，然后思考如何迁移应用到自己的研究方向上。
在这里插入图片描述

从直观上理解VAE

变分自编码器（Variational Auto-Encoders，VAE）是深度生成模型的一种形式（GAN也是其中一种），VAE是基于变分贝叶斯推断的生成式网络结构。传统自编码器是通过数值方式描述潜在空间的不同，而VAE以概率的方式描述潜在空间的不同，是一种无监督式学习的生成模型。

举个简单的例子说明变分自编码模型，输入一张照片，想描述其中人物的笑容，如果用笑/没笑这样的二分类/某个单值表示则显得不是很适合（注：单值表示则是自编码器模型的特点）。更好的表述应该是用一个区间范围来表示笑的概率大小，如下图即是通过VAE的编码（encoder）得到图片中笑的概率分布情况。
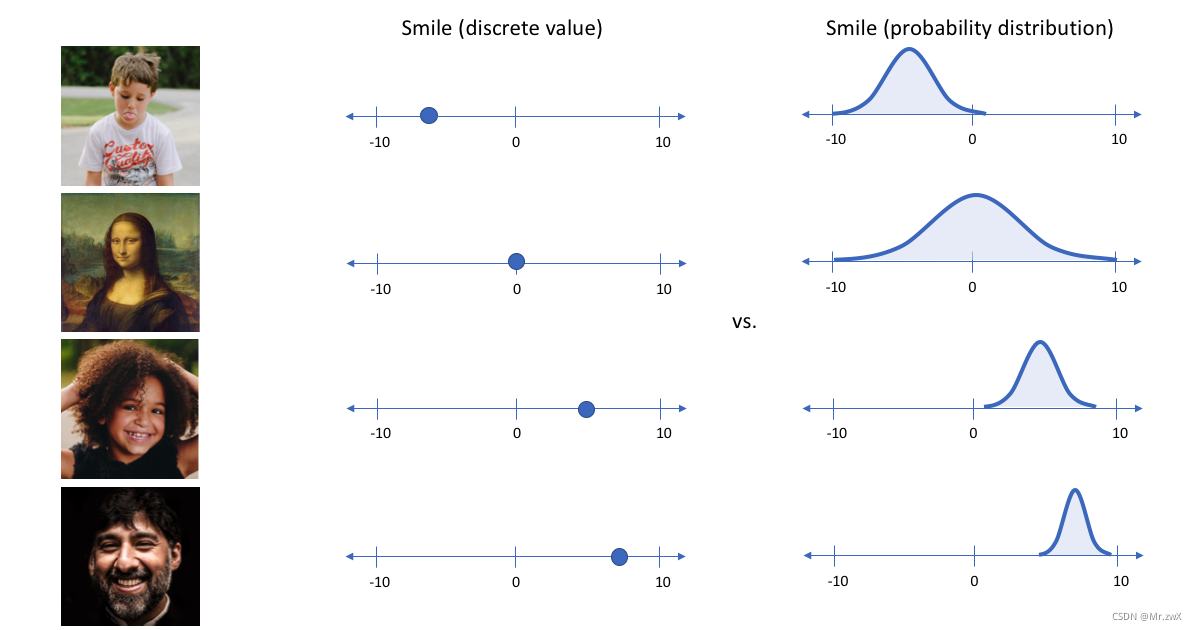
在这里插入图片描述

通过VAE，可以将每一个特征表示为概率分布。那么如何通过这个概率分布来生成新的数据呢？这个过程叫做解码（decoder），从每个潜在状态分布中随机采样，生成一个向量，作为解码器模型的输入，从而得到新生成的结果。如下图所示，一张图片中的人物几大特征（smile skin gender beard…）通过encoder编码后生成不同特征的概率分布，这样能使decoder重新构建我们的输入。
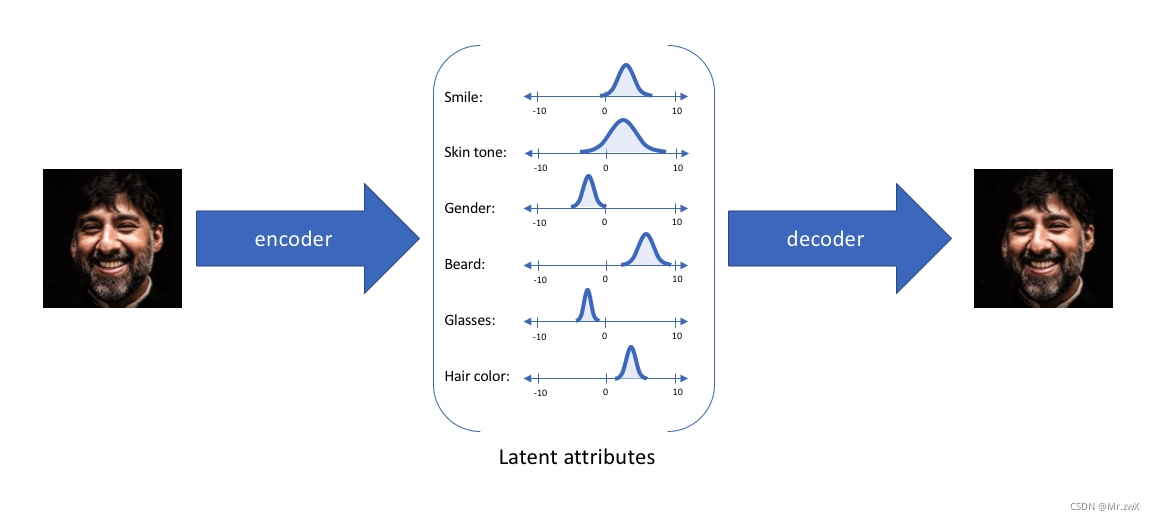
在这里插入图片描述

VAE模型结构

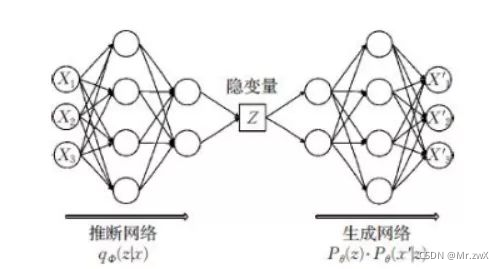
现在学习VAE的模型结构是什么样的。如下图所示，模型分为两个部分：推断网络（编码器encoder）和生成网络（decoder）。

推断网络：用于原始输入数据的变分推断，生成隐变量的变分概率分布情况；
生成网络：根据生成的隐变量变分概率分布还原为原始数据近似概率分布。

在VAE中，假设 $p (Z ∣ X)$ （后验分布）是满足正态分布的。给定一个真实样本 $K_k$ ，假设存在一个专属于 $X_k$ 的分布 $p(Z|X_k)$ ，进一步假设这个分布是正态分布（独立的、多元的）。由于这个专属性，有多少个样本X就有多少个正态分布，能更好让decoder做还原。

变分自编码器和自编码器有什么根本上的区别呢？变分自编码器的encoder和decoder的输出都是受参数约束变量的概率密度分布，而自编码器是某种特定数值的编码。
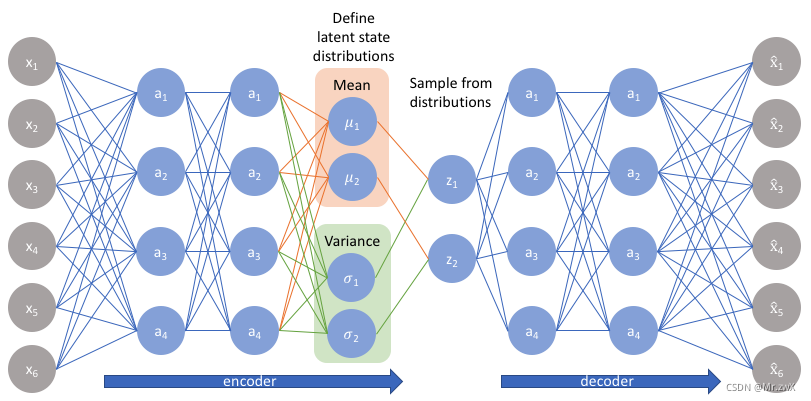
在这里插入图片描述

VAE原理分析

想根据观察到的x，推断出潜在空间的分布：
$p(z|x)=\frac{p(x|z)p(z)}{p(x)}$
计算 $p (x)$ 是很复杂的，
$p(x)=\int{p(x|z)p(z)}dz$
通常是个复杂的分布，我们可以用变分推断来估计这个值。
我们用另一个分布 $q (z ∣ x)$ 近似估计 $q (z ∣ x)$ ，将 $q (z ∣ x)$ 定义为具有可伸缩性的分布。
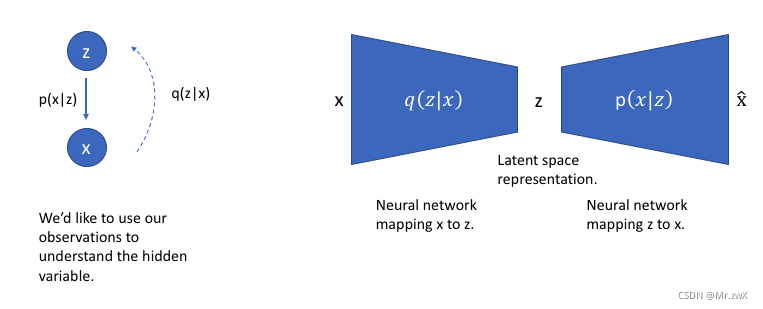在这里插入图片描述使用 $q$ 来推断可能隐藏的变量（潜在状态），这些变量可以用于生成观察值。我们可以进一步将这个模型构造成神经网络结构，其中编码器模型（encoder）学习从 $x$ 到 $z$ 的映射，解码器模型（decoder）学习从 $z$ 到 $x$ 的映射。

KL散度
KL散度是两个概率分布的差值，要想保证 $q (z ∣ x)$ 与 $q (z ∣ x)$ 尽可能相似，我们的目的即是最小化这个KL散度：
$m i n K L (q (z ∣ x) ∣ ∣ p (z ∣ x))$
转换一下，通过最大化下式，即最小化了上式：
$E_{q(z|x)}logp(z|x)-KL(q(z|x)||p(z))$
其中， $E_{q(z|x)}logp(z|x)$ 表示重构的可能性， $m i n K L (q (z ∣ x) ∣ ∣ p (z ∣ x))$ 表示要学习的分布 $q (z ∣ x)$ 有多逼近真实的后验分布 $p (z ∣ x)$ .

损失函数
损失函数包含两部分：
$L(x,\hat{x})+KL(q(z|x)||p(z))$

分布标准化处理
有博主把这一部分写得非常清楚，借鉴一部分过来供大家理解学习，出处附在参考资料中。
在这里插入图片描述

重参数技巧（reparameterization trick）
为什么要用重参数技巧？在decoder过程中，我们要从 $p (z ∣ x)$ 中采样一个 $z$ 出来，尽管采样的结果 $p (z ∣ x)$ 是一个分布（已知高斯分布的参数，故可求导训练），但是随机采样这个过程是不可求导训练的。
如何解决这个问题？用重参数技巧。从 $N(\mu,\sigma^2)$ 中采样一个 $z$ 出来，相当于从 $N (0, I)$ 中采样一个 $\epsilon$ 出来，然后做参数的线性变换让 $z=\mu+\epsilon\times\sigma.$
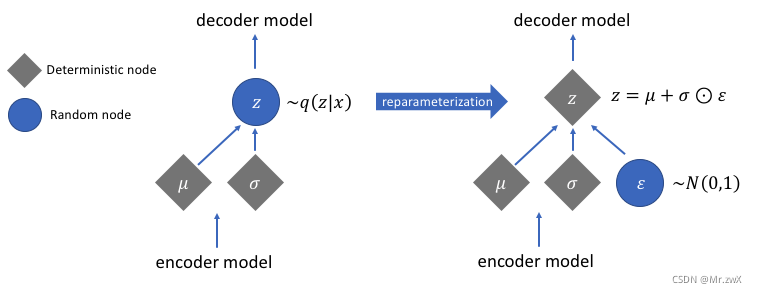
在这里插入图片描述

图生成模型：变分图自编码器（VGAE）

主要思想
将变分自编码器（VAE）迁移到图领域中（graph），将已知图通过图卷积层（GCN）编码（decoder），学习到节点向量表示的分布，在分布中采样得到节点的向量表示，然后解码（link prediction）重构图。

模型结构
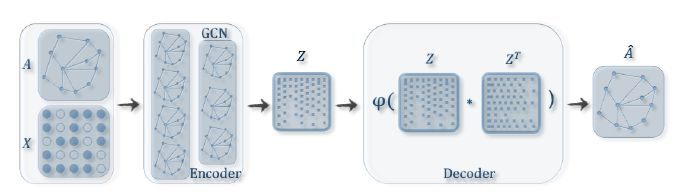
在这里插入图片描述
输入：邻接矩阵A和特征矩阵X
过程：通过编码器（图卷积网络）学习节点低维向量表示的均值 $\mu$ 和方差 $\sigma$ ，然后用解码器（链路预测）生成图。
编码器是简单的两层GCN网络：
$q(Z|X,A)=\sum_{i=1}^N q(z_i|X,A)$
其中， $q(z_i|X,A)=N(z_i|\mu_i,diag(\sigma^2))$ ， $\mu$ 是节点向量表示 $\mu = GCN_{\mu}(X,A)$ 的均值， $\sigma$ 是节点向量表示的方差 $log\sigma=GCN_\sigma(X,A)$ 。
两层卷积网络定义如下：
$GCN(X,A)=\widetilde{A} ReLU(\widetilde{A}XW_0)W_1$
其中， $\widetilde{A}=\widehat{D}^{-\frac{1}{2}}\widehat{A}\widehat{D}^{-\frac{1}{2}}$ ， $\widehat{A}=A+I$ ， $\widehat{D}$ 是 $\widehat{A}$ 对应的度矩阵。
值得注意的是， $GCN_{\mu}(X,A)$ 和 $GCN_\sigma(X,A)$ 共享参数 $W_0$ ，而各自的 $W_1$ 不同。采样过程和VAE相同，都是用了重参数技巧（reparameterization trick）。

解码器两两计算两点间存在边的概率来重构图：
$p(A|Z)=\sum_{i=1}^N\sum_{i=1}^Np(A_{ij}|z_i, z_j)$
故有， $p(A_{ij}=1|z_i,z_j)=sigmoid(z_i^Tz_j)$ 。

损失函数
损失函数包含两部分：生成图和原始图之间的距离度量、节点表示向量分布和正态分布的散度。
$L=E_q(Z|X,A)[logp(A|Z)]-KL[q(Z|X,A)||P(Z)]$
其中， $E_q(Z|X,A)[logp(A|Z)]$ 是交叉熵损失函数。

图自编码器

除了VGAE，还有GAE模型——图自编码器。
编码器仍然是两层GCN网络：
$Z = G C N (X, A)$
解码器通过两两计算两点间存在边的概率来重构图：
$\widetilde{A}=sigmoid(ZZ^T)$
损失函数衡量了生成图和原始图之间的差异值：
$L=E_{q(Z|X,A)}[logp(A|Z)]$
可以发现，GAE与VGAE相比少了变分，即少了概率表征这一特点，所以损失函数中不需要再加入KL散度。