[人工智能]论文理解 —— Adversarial Imitation Learning with Trajectorial Augmentation and Correction

• 标题：Adversarial Imitation Learning with Trajectorial Augmentation and Correction
• 会议：ICRA 2021
• 文章链接：Adversarial Imitation Learning with Trajectorial Augmentation and Correction
• 全文翻译：论文翻译 —— Adversarial Imitation Learning with Trajectorial Augmentation and Correction
• 领域：模仿学习 - 轨迹级数据增强

1. 前置内容

1.1 模仿学习中的数据增广

• 本文致力于将轨迹级的数据增广方法引入模仿学习（IL），以减少所需专家数据的数量。
  1. 数据增广通常用于计算机视觉任务，通常的方法是对输入图像进行扭曲变形处理，通过施加相关扰动（例如平移、旋转）增大标记数据集
  2. 模仿学习的问题设定和强化学习类似，智能体可以与环境进行交互，区别在于环境不再提供任何形式的奖励/成本信号，取而代之的是一些专家提供的轨迹样本，智能体要从这些示范数据中学习一个最优策略。通常我们假设专家策略是最优的，因此模仿学习的目标等价于找到专家策略
• 在过去的方法中，只有行为克隆类（BC）的 IL 方法可以做数据增广，因为这类方法的本质是匹配单步动作，而构造一个虚拟的专家级 (s,a) 二元组通常是比较简单的。对单个 (s,a) 二元组进行数据增广的这类方法忽略了轨迹的马尔可夫性，作为一条完整的轨迹，先后的状态之间是相关的，各个 (s,a) 二元组之间并非独立同分布，因此构造的虚拟 (s,a) 样例难以扩展为一条轨迹

1.2 生成对抗模仿学习（GAIL）

• 本文方法基于GAIL，这是一种使用生成对抗式结构的IL方法，于2016年被提出。它使用策略网络充当GAN中的生成器，每轮迭代中，策略网络和环境交互生成一条轨迹，然后更新判别器参数，使其尽量区分专家轨迹和生成的轨迹，然后固定判别器，以判别器得分取对数作为奖励函数，执行TPRO算法更新策略网络的参数。
  
• GAIL框架的示意图如下
  
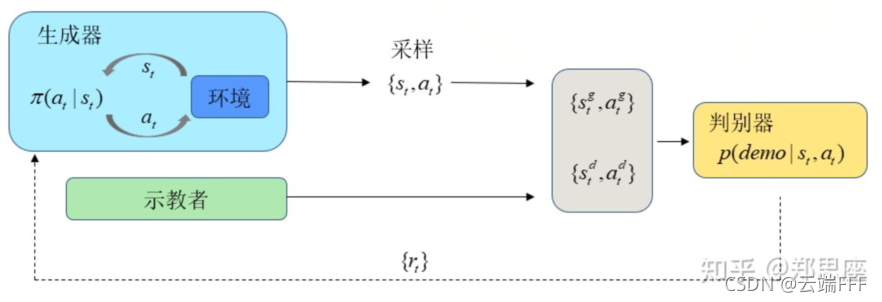
• 从宏观上来说，这个GAIL其实就是GAN的一种特例，带有参数 $\theta$ 的策略网络 ${\pi }_{\theta }$ 生成轨迹，试图欺骗带有参数 $w$ 的判别器 $D_w$，$D_w$ 试图区分真正的专家策略 ${\pi }_E$ 与生成的样本。因此，判别器的损失是
  $$L_w=?{\mathbb{E}}_{{\pi }_E}[log{D}_w(s,a)]?{\mathbb{E}}_{{\pi }_{\theta }}[log(1?D_w(s,a))]$$
  同时，生成器的损失为
  $$L_{\theta }={\mathbb{E}}_{{\pi }_{\theta }}[log(1?D_w(s,a))]$$
  为了获得 $D_w$ 相对于 ${\pi }_{\theta }$ 的期望，GAIL 将其建模为 RL 成本函数，并使用诸如 TRPO 之类的梯度方法对其进行近似（也就是说生成器是一个RL方法）

2. 本文方法

2.1 增广轨迹的生成和矫正

• 为了生成虚拟的专家轨迹，作者的想法很直观，就是类比传统数据增广方法，向已有的专家轨迹中加入扰动。对于专家轨迹 τ E = { ( s E 1 , a E 1 ) , ( s E 2 , a E 2 ) . . . } \tau_E = \{(s_{E_1},a_{E_1}),(s_{E_2},a_{E_2})...\} τE?={(sE1??,aE1??),(sE2??,aE2??)...} ，对动作序列施加扰动后得到新的动作序列 $q$
  q = { a 1 ′ , a 2 ′ , a 3 ′ . . . } , ?? w h e r e ??? a t ′ = a E t + v q = \{a_1',a_2',a_3'...\},\space\space where \space\space\space a_t' = a_{E_t} + v\\ q={a1′?,a2′?,a3′?...},??where???at′?=aEt??+v

• 由于马尔可夫性，专家轨迹中的状态序列已经没用了，重新按照 $q$ 序列和环境交互，会得到一条扰动后的增广轨迹。显然，由于级联误差的影响，这个轨迹很可能是不成功的（即无法完成任务），虽然如此，但文章表示 “这些序列仍然包含有用的信息，并且有可能通过对其行为进行小幅修正而取得成功”，所以作者引入了轨迹校正增强 (Corrected Augmentation for Trajectories, CAT) 框架来修改动作序列 $q$，希望矫正后的动作序列引导的轨迹能够成功
  

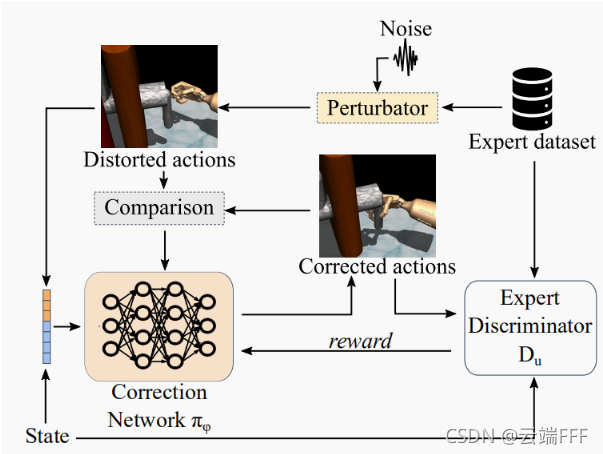
• CAT框架如上所示，这个框架是基于GAIL方法的，其中矫正网络 ${\pi }_{?}$ 作为 “生成器”，和判别器 $D_u$ 要相互对抗。注意，这里的 “生成器” 并不直接和环境交互来生成轨迹，而是对扰动动作序列引导的轨迹中的动作序列进行调整

  1. 判别器：目标是将生成的样本与真实专家（fixed real experts）分开。由于未标记数据不是其目标的一部分，因此其损失与 GAIL 相同
     $$L_u=?{\mathbb{E}}_{{\pi }_E}[log{D}_u(s,a)]?{\mathbb{E}}_{{\pi }_{?}}[log(1?D_u(s,a))]$$
  2. 生成器（矫正网络）：一方面和GAIL中一样，要试图最大化鉴别器的奖励（得分），也就是让其选择的动作尽量像专家的选择，另一方面还要最小化生成的动作与扰动失真的专家动作序列之间的差异，因此，这里需要扰动动作 $a^{\prime }$ 作为辅助。总的来说，CAT框架和GAN框架的主要区别就在于其生成器目标多了一个贴近扰动后动作 $a^{\prime }$ 的项
     $$L_{?}={\mathbb{E}}_{{\pi }_{?}}[log(1?D_u(s,a))]+\gamma ||a?a^{\prime }|{|}_2^2$$

• CAT部分的伪代码如下
  
  分析这个过程，我们首先对所有专家轨迹的动作序列施加扰动，得到扰动后的动作序列集合 $Q$，然后遍历这个集合，用每个扰动动作序列 $q_i$ 和环境交互来得到扰动轨迹 ${\tau }_i$，接下来，把 ${\tau }_i$ 拆开成一系列状态动作二元组，先计算判别器损失，梯度更新判别器参数 $u$；然后用矫正网络 ${\pi }_{?}$ 对轨迹中每个状态动作二元组给出一个矫正动作，计算生成器损失，梯度更新矫正网络参数 $?$

• 总的来说，CAT网络训练完成后，我们得到一个矫正网络 ${\pi }_{?}$，可以把随机扰动的轨迹尽量修改得像是专家生成的一样。这样一来，为了得到一条增广的专家轨迹，只要进行以下步骤

  1. 对某条专家轨迹施加各种随机扰动，得到扰动后的动作序列
  2. 用扰动的动作序列和环境交互，得到扰动轨迹
  3. 用矫正网络 ${\pi }_{?}$ 矫正扰动轨迹，得到矫正动作序列
  4. 用矫正的动作序列和环境交互，得到矫正轨迹，可以作为增广的专家轨迹

  因为这个框架训练完成之后具有了给出新的专家轨迹数据的能力，所以文中将训练好的CAT框架称为 “合成专家”，甚至还可以训练多个矫正网络以获取多个 “合成专家”，理论上，每个 “合成专家” 都能给出无限的增广轨迹

• 虽然没有说明，但是本文隐含地对于状态和动作空间做了如下假设

  1. 所有状态下的可选动作集合都是一致的·
  2. 动作空间是连续的

2.2 使用增广轨迹进行模仿学习

• 注意，CAT框架中，虽然进行了矫正，但并不能保证矫正后的轨迹一定成功。为此，作者引入了一个成败过滤器，利用环境的先验知识判断增广的轨迹能否成功，从而过滤出所有能成功完成任务的增广轨迹，然后就可以直接用GAIL方法进行模仿学习了
• 作者在文中把该框架称为数据增广模仿学习（Data Augmented Generative Imitation, DAugGI)，示意图如下
  
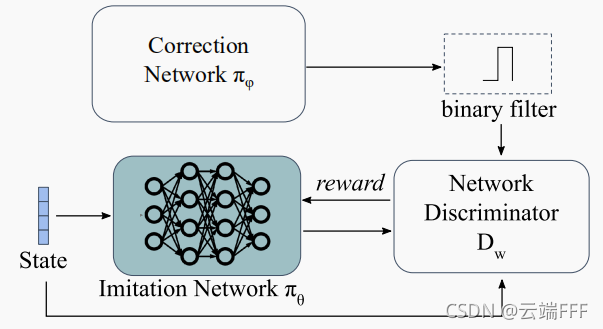
  这其实就是一个GAIL方法的变型，DAugGI 策略网络 ${\pi }_{\theta }$ 的目标是匹配专家分布，因此其损失函数与 GAIL 的生成器相同
  $$L_{\theta }={\mathbb{E}}_{{\pi }_{\theta }}[log(1?D_w(s,a))]$$
  另一方面，鉴别器 $D_w$ 试图区分 CAT 矫正网络 ${\pi }_{?}$（“合成专家”） 和 DAugGI 策略网络（生成器） ${\pi }_{\theta }$ 生成的样本，而不是 GAIL 中的 ${\pi }_{\theta }$ 和 ${\pi }_E$。因此，判别器 $D_w$ 的损失为
  $$L_w=?{\mathbb{E}}_{{\pi }_{?}}[log{D}_w(s,a)]?{\mathbb{E}}_{{\pi }_{\theta }}[log(1?D_w(s,a))]$$

2.3 方法总览

• CAT 和 DAugGI 是两个相对独立的对抗过程，把它们结合起来，就得到了本文方法的总览，如下图所示
  

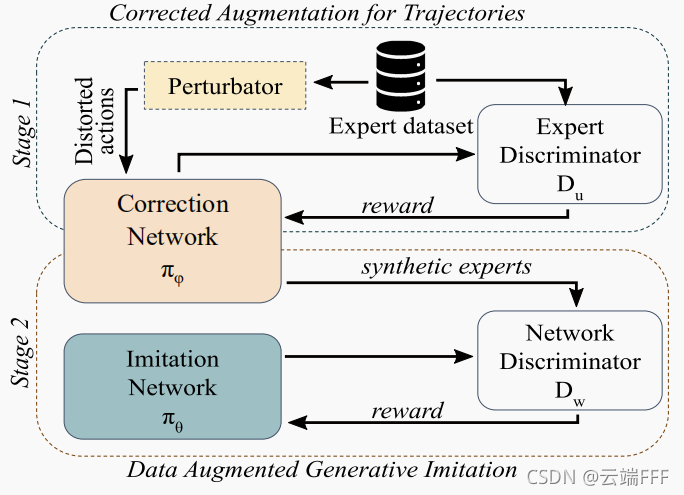
3. 实验结论

• 本文在五个环境中进行了实验，其中两个是OpenAI的经典控制问题（由3位人类专家提供示教），三个是复杂的机械手控制问题（由25位人类专家提供示教）
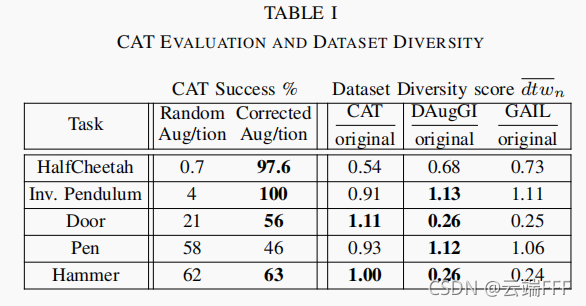
• 上表左边给出了随机扰动轨迹和CAT纠正轨迹的成功率对比，右边给出了CAT生成轨迹、使用CAT训练DAugGI学到策略引导的轨迹、使用原始专家数据训练GAIL学到的策略引导的轨迹的多样性和原始专家轨迹多样性的比值。可见
  1. CAT 几乎总是能够成功纠正失真的动作。最具挑战性的是 Pen 任务，这个任务难度较大，导致了无效的纠正。尽管如此，它的轨迹并没有模式崩溃，其多样性仍非常接近原始示范
  2. 由于 CAT 由大量相似的轨迹引导，其多样性比其他网络小，这是预期内的。令人鼓舞的是，DAugGI 网络的多样性不仅与 GAIL 非常接近，而且在大多数情况下甚至略高于它。这表明 CAT 生成的增广轨迹可能比原始专家数据集泛化得更远
• 随着训练步数增加，性能变化如下所示。其中DAugGI 使用 CAT 增强的轨迹进行训练，GAIL仅使用有限的原始专家轨迹进行训练，DDPG 是使用 DAugGI 中二分类器的成败状态作为0-1奖励执行RL的结果
  
  1. 左侧的五张图说明，由于任务难度不同，出现了不同的响应。非常简单或很困难的任务，例如 InvertedPendulum 和 Pen，DAugGI 的行为似乎与 GAIL 非常相似。这是因为任务要么已经很容易解（InvertedPendulum），要么 “坏” 老师不提供任何额外的信息（Pen）。但即便如此，它似乎不仅保留了原始信息，还增加了稳定性。 中等难度的任务，如 HalfCheetah 和 Door，是受益最大的任务，DAugGI 显示出明显的改进。 对于另一个中等难度的 Hammer 任务，DAugGI 设法大大提高了其稳定性，而 GAIL 的收敛能力非常不稳定。所有 DDPG 运行都无法收敛，这意味着每个轨迹末尾的成败过滤器信号对于纯 RL 方法来说信息不足。[5] 中也报告了类似的发现，其中使用了稀疏奖励。 此外，我们评估了专家数据集大小的重要性。
  2. 右侧的两张表明，即使在专家很少的极端情况下，DAugGI 也可以提高整体性能，而 GAIL 通常在这种情况下表现不佳
• 详细的实验结果参照原文：论文翻译 —— Adversarial Imitation Learning with Trajectorial Augmentation and Correction

4. 结论 & 分析

• 这项工作提出了一个控制系统的数据增强框架。由于轨迹的（马尔可夫）性质，不能保证失真后的轨迹会保留它们的标签（轨迹成功与否）。因此，作者开发了一个半监督校正网络，该网络用失真扭曲的专家动作引导并产生合成专家轨迹。实验表明，校正网络不仅可以捕获至少相等且通常更好的动作空间表示，而且还可以为模仿智能体提供更快、更稳定和同样多样化的训练环境。目前工作的潜在扩展是
  1. 将其转化为相互学习，以便两个网络相互帮助
  2. 将多样性度量纳入训练过程
  3. 在现实生活环境中应用该框架，比如用在具有结构化噪声的 near-expert trajectories 上
• 我认为这项工作的问题在于
  1. 隐含地对于状态和动作空间做了两个假设：所有状态下的可选动作集合都是一致的；动作空间是连续的
  2. 在环境中执行随机扰动的动作可能很危险，特别是在现实环境中
  3. 本文方法获得增广的轨迹都是比较差的轨迹，比如机器手开门任务，专家轨迹都是直接拉把手开门，而随机扰动再矫正的轨迹很可能是哆嗦半天再开门。如果仅从成功率这个指标看，确实可能会有提升，但若从其他指标看（比如完成任务的耗时），很可能性能反而下降了，这是本文的最大问题。本文方法可能仅在专家数量特别稀缺的情况下比较有效，因为至少可以增大完成任务的可能性。事实上，如果我们任务专家轨迹是最优的，那么通过施加扰动来做增广几乎一定只能获得次优轨迹。若能找到其他更好的轨迹增广方法，将是发文章的好机会