从零开始实现线性回归
本文根据李沐在b站的课程【动手学深度学习v2】
1、根据带有噪声的线性模型构造一个人造数据集。使用线性模型参数 w = [ 2 , ? 3.4 ] T 、 b = 4.2 w=[2,-3.4]^T、b=4.2 w=[2,?3.4]T、b=4.2和噪声项生成数据集及其标签:
y = X w + b + ? y=Xw+b+? y=Xw+b+?
import random
import torch
from d2l import torch as d2l
import os
os.environ['KMP_DUPLICATE_LIB_OK'] = 'TRUE'
def synthetic_data(w, b, num_example):
"""生成 y=Xw+b+噪声"""
# 均值为0方差为1的随机数,num_example个样本,列数是w长度
X = torch.normal(0, 1, (num_example, len(w),))
print(X)
y = torch.matmul(X, w) + b
print(y)
# 均值为0方差为0.01,形状和y相同
y += torch.normal(0, 0.01, y.shape)
# 将y作为列向量返回
return X, y.reshape((-1, 1))
true_w = torch.tensor([2, -3.4])
true_b = 4.2
features, lables = synthetic_data(true_w, true_b, 1000)
print("features:", features[0], '\nlables:', lables[0])
d2l.set_figsize()
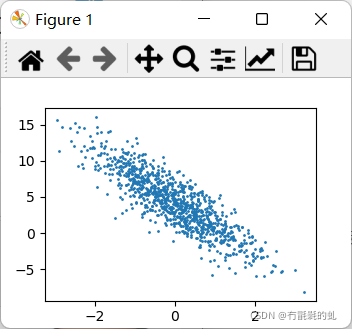
d2l.plt.scatter(features[:, 1].detach().numpy(), lables.detach().numpy(), 1)
d2l.plt.show()
打印出的图像
- 如果出现以下问题
OMP: Error #15: Initializing libiomp5md.dll, but found libiomp5md.dll already initialized.
OMP: Hint This means that multiple copies of the OpenMP runtime have been linked into the program. That is dangerous, since it can degrade performance or cause incorrect results. The best thing to do is to ensure that only a single OpenMP runtime is linked into the process, e.g. by avoiding static linking of the OpenMP runtime in any library. As an unsafe, unsupported, undocumented workaround you can set the environment variable KMP_DUPLICATE_LIB_OK=TRUE to allow the program to continue to execute, but that may cause crashes or silently produce incorrect results. For more information, please see http://www.intel.com/software/products/support/.
- 加上以下代码即可解决
import os
os.environ['KMP_DUPLICATE_LIB_OK'] = 'TRUE'
经过以上步骤我们的训练样本就准备好了
2、编写函数,实现每次读取一个小批量
#省略以上代码
def data_iter(batch_size, features, lables):
num_examples = len(features)
indices = list(range(num_examples))
# 样本随机读取,没有顺序,shuffle打乱indices
random.shuffle(indices)
# 从0开始到num_examples,每次跳batch_size个大小
for i in range(0, num_examples, batch_size):
#从i开始,到i + batch_size
batch_indices = torch.tensor(
indices[i:min(i + batch_size, num_examples)])
print('i',i)
print("batch_indices",batch_indices)
yield features[batch_indices], lables[batch_indices]
batch_size = 5
for x, y in data_iter(batch_size, features, lables):
print(x, '\n', y)
break
- 这里注意yield的用法
3、定义模型,定义损失函数,定义优化算法
- 定义模型
y = X w + b y=Xw+b y=Xw+b - 损失函数
l o s s = ( y ^ ? y ) 2 2 loss=\frac {(\hat{y}-y)^2}2 loss=2(y^??y)2?
# 定义模型
def linreg(X, w, b):
'''线性回归模型'''
return torch.matmul(X, w) + b
# 定义损失函数
def squared_loss(y_hat, y):
'''均方损失'''
return (y_hat - y.reshape(y_hat.shape)) ** 2 / 2
# 定义优化算法
# params包含w和blr学习率
def sgd(params, lr, batch_size):
'''小批量梯度下降'''
with torch.no_grad():
for param in params:
param -= lr * param.grad / batch_size
param.grad.zero_()
# 定义初始化参数模型
w = torch.normal(0, 0.01, size=(2, 1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)
4、训练过程及评估结果
lr:学习率
num_epochs :分包的数量,即训练几次
# 训练过程
lr = 0.03
num_epochs = 3
net = linreg
loss = squared_loss
for epoch in range(num_epochs):
for X, y in data_iter(batch_size, features, lables):
l = loss(net(X, w, b), y)
l.sum().backward()
sgd([w, b], lr, batch_size)
with torch.no_grad():
train_l = loss(net(features, w, b), lables)
print(f'epoch {epoch + 1},loss{float(train_l.mean()):f}')
# 比较真实参数和通过训练学到的参数来评估训练成功的程度
print(f'w的估计误差:{true_w - w.reshape(true_w.shape)}')
print(f'b的估计误差:{true_b - b}')
我的输出结果:
epoch 1 , loss 0.049434
epoch 2 , loss 0.000246
epoch 3 , loss 0.000053
w的估计误差:tensor([ 0.0006, -0.0012], grad_fn=)
b的估计误差:tensor([0.0008], grad_fn=)
总结
可以手动调节几个超参数体验一下变化。
- 比如将学习率lr调的更小,比如lr=0.001,结果:
epoch 1 , loss 13.877259
epoch 2 , loss 11.297474
epoch 3 , loss 9.197680
w的估计误差:tensor([ 1.5019, -2.4621], grad_fn=)
b的估计误差:tensor([3.0993], grad_fn=) - 可以看到误差还是很大的。可以让模型多训练几次,num_epochs=10
epoch 1 , loss 13.567297
epoch 2 , loss 11.112944
epoch 3 , loss 9.102850
epoch 4 , loss 7.456498
epoch 5 , loss 6.108027
epoch 6 , loss 5.003509
epoch 7 , loss 4.098810
epoch 8 , loss 3.357737
epoch 9 , loss 2.750709
epoch 10 , loss 2.253470
w的估计误差:tensor([ 0.7045, -1.2464], grad_fn=)
b的估计误差:tensor([1.5734], grad_fn=) - 试试将lr调的很大,lr=5:
epoch 1 , loss nan
epoch 2 , loss nan
epoch 3 , loss nan
w的估计误差:tensor([nan, nan], grad_fn=)
b的估计误差:tensor([nan], grad_fn=) - 结果出现错误。这就说明了学习率不能太大也不能太小