2021年国赛B题-乙醇制备C4烯烃原题
第五讲：国赛B题第一小问讲解
2021年国赛B题-乙醇制备C4烯烃数据：
数据一：
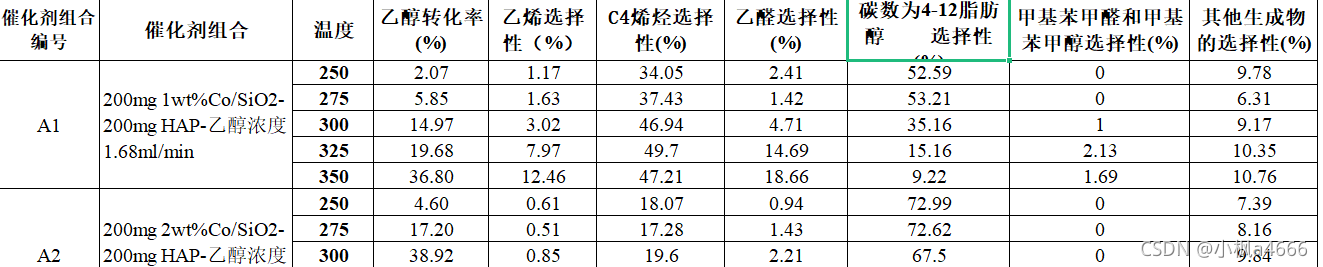
数据二：
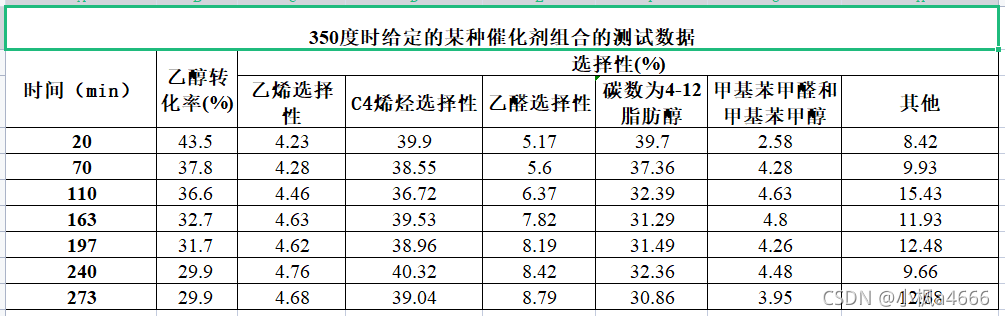
开始建模
观察此题，就是一个统计推断问题，采取回归思想以及方差分析以及差值算法以及相关分析即可解决。
??????????????????????????????????????????????????????????????????????
先别急着写摘要和问题分析，为什么？
很简单，假如你建模建模突然换了模型，你摘要和问题分析是不是得重写了？
??????????????????????????????????????????????????????????????????????
先写模型假设，模型都是理想化的，建立模型就必须提出假设
很简单啦，比如：
模型假设 1.假设收集的数据和资料的数据真实可靠 2.假设模型考虑内在因素，不考虑外在因素的影响 3.模型的误差在允许的范围内 一元线性回归模型对本模型具有适用性
好嘞，假设写好了，现在我们就可以直接写模型求解，模型求解过程中遇到的符号顺便写入三线表中，三线表怎么写我就不说了，给你例图自己看。
好嘞，竟然知道用什么模型了，那就直接开写了！
??????????????????????????????????????????????????????????????????????
首先啥是C4烯烃啊，我们可以普及普及知识，还可以蹭参考文献，学到了吗？
好嘞，现在开始建模，问题一是研究啥？
每种催化剂组合，分别研究乙醇转化率、C4 烯烃的选择性与温 度的关系？
这不就是一元线性回归吗？好嘞啥也不管，公式套上去！
那我们写完就是这样：
这里我公式没写完整哈，还有b呢，加分项啊，写完公式。
好了好了，结束了啊！来句：
具体结果见问题一模型求解部分，XX页。以下我们进行该模型的检验（模型检验嘛，灵敏度分析更好，灵敏度分析是啥我也不懂，自己查百度）
好嘞，模型不就建立好了嘛，然后建立模型的检验，一元线性回归，回归模型怎么检验啊？忘记了嘛？
回归模型的检验当然是对误差的检验了！根据所学知识有下面几种：
1.SSE标准误差检验：（这里n是样本点数量，其他的不讲了）
写出来了直接说结果，然后根据你的SE值说明误差情况，一般不用此方法检验。
2.拟合优度检验（看不懂吧，那不妨看第二张图片，你就懂了怎么算了，具体不讲）
这个值一般是越大越好，越接近1，越是正相关，-1越是负相关，如果低于0.6说明你和性较差，模型不适合。
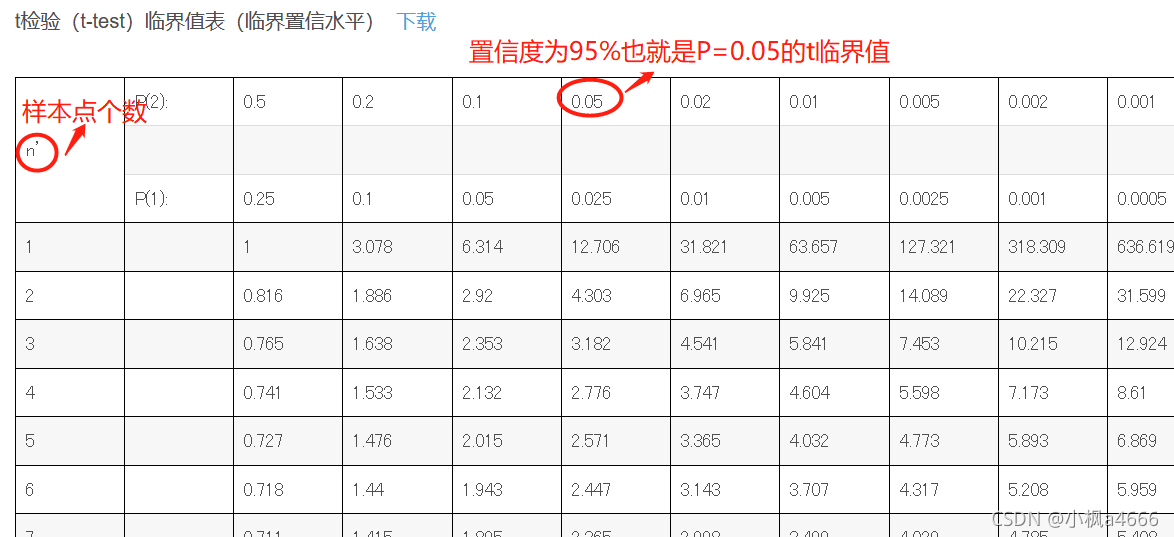
3.T检验
T检验也叫做回归系数检验，这里b就是指你求出的回归系数，x为样本点自变量，求出的tb及时T 检验值。
**说明一下，图中n为自由度df=样本点个数N -1
检验出来大小和对应的表进行查找，如果小于临界值说明模型适合，可以使用。
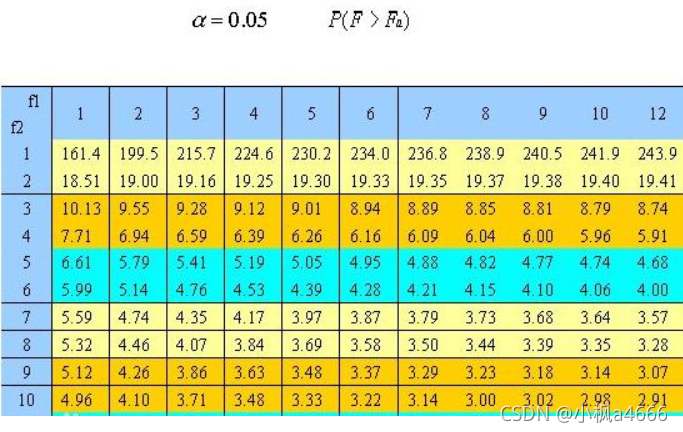
4.F检验
嗯，不说了这检验，都看得懂，就是这么个除法，这么比较呢？和t检验一样，也有一个临界值表，叫做F临界值表，标明不同自由度不同置信区间下F临界值（我们一般取0.05啊,也就是p=0.05的犯错误概率下）
好嘞，检验模型我们写完了，我这里大致就是这么写：
好了，第一问第一小问模型不就构建完毕了吗？现在写Python给我们算出的结果呗
以下是Python对第一问的部分代码，这里简单说一下，不讲
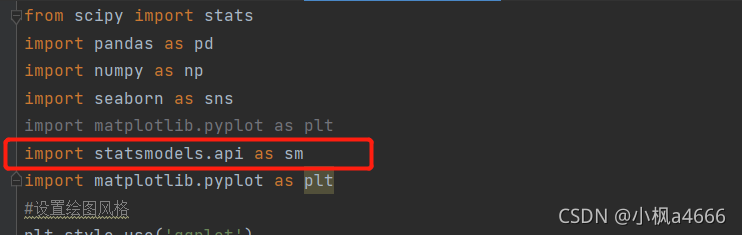
这画圈的就是导入Python自带的回归分析包，结下来读取数据对吧，数据肯定是个样本点（散点形式）
因此我们不妨画图看看分布特征，这里直接用seaborn包的三点回归图
import seaborn as sns 样式画图包
import matplotlib.pyplot as plt 基础画图包
cat = pd.read_csv(r'乙醇转化率和温度关系.csv') 导入附件csv数据
sns.lmplot(x='a', y='b', data=cat) 画图
plt.show() 展示图
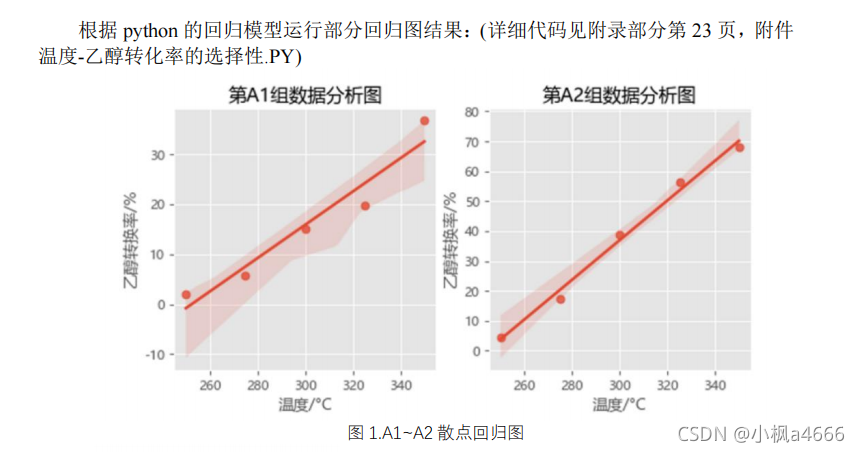
看结果
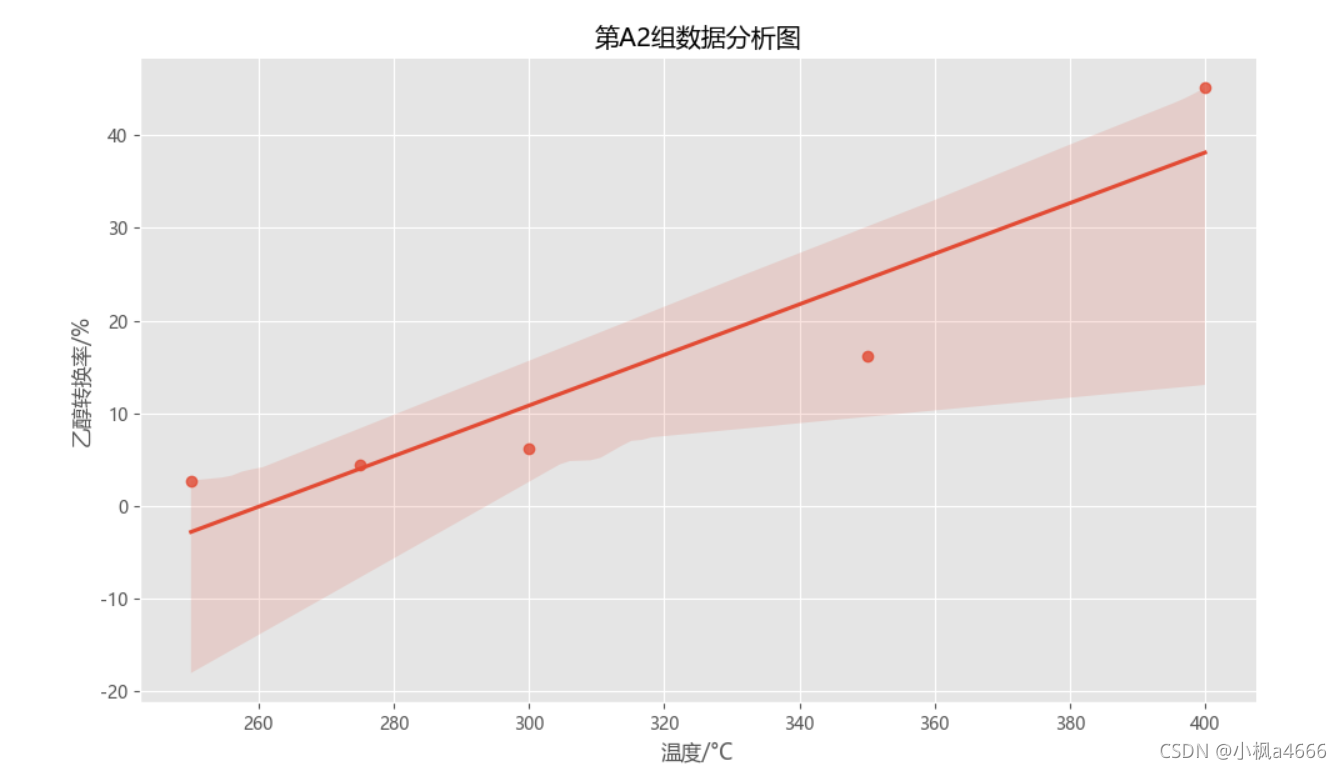
很给力，就是这样的图，我们可以复制上面了呗
现在既然我们刚才导入回归分析包，就回归分析呗，直接上代码
fit = sm.formula.ols('b ~ a', data=cat).fit()
# 返回模型的参数值
print(fit.params)
b,a是啥，我给你看样本数据你就懂了！
a,b
250,1.408181826
275,3.417913913
300,6.723725762
350,19.30926263
400,43.59544439
250,2.763024157
275,4.402661072
300,6.22356275
350,16.1870321
400,45.13523908
知道了吧，sm.formula.ols就是回归分析包的函数呗，我也不懂为啥这么写，用就行了呗，fit.params就是适合性模型结果，我们print打印出来
看结果：
这不就是截距和回归系数嘛，好咧，第一个回归模型不就出来了嘛！附件好像是每种都要回归，那就加个for循环呗，不断的从附件取数据，分析，结果，取数据，分析，结果。这么循环我就不讲了，这是Python的内容！
总之，我们最终把结果整理为一个表，就是这样
是不是可以贴在论文模型求解的结果处，那你也可以贴点图蹭下论文页数，千万别蹭多，多的放附录后面，并在此标明去处！
是不是很牛逼？
??????????????????????????????????????????????????????????????????????
问题一的第一小问还要研究和C4烯烃的，一样呗，算算算嘛：
当然，你结果贴完了，你得写结论啊，这样写，自己看，不多讲：
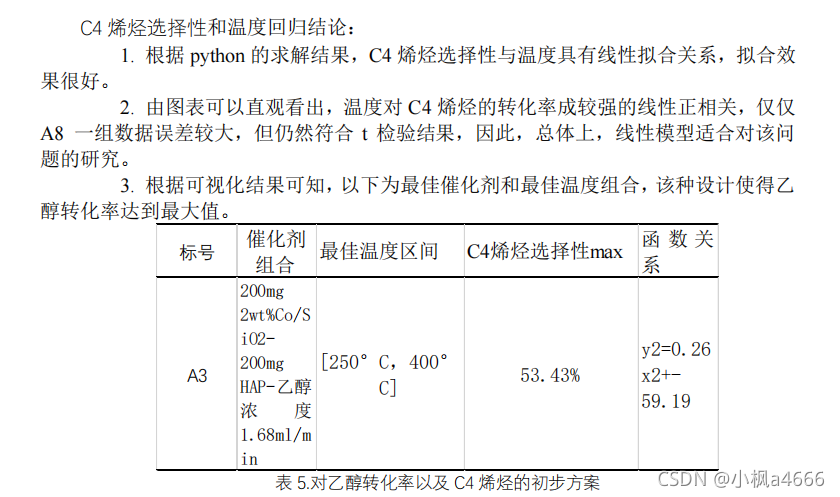
第一问第一小问结束了，快不快？说快也快，前提你得练过。
??????????????????????????????????????????????????????????????????????
看第一问还没完，第二小问，什么350 度时给定的催化剂组合在一次实验不同时间的测试结果进行分析。根据附件二：
附件二是啥，看看
眨眼一看，不就是350度不同时间不同项目的情况嘛？叫我们分析分析，
那就简单分析呗，比如随时间变化，比如各项之间关系，那这么分析？最直观？
当然是画图！另外各项之间关系，那就相关分析呗，看看各项之间的关联度，顺便画一个相关热力图，不就更直观了嘛，最后写个结论。
这是可视化画图，别问用什么画的，用那就是echarts,HTML网页画的，这里不讲怎么画，不会那就用Excel画吧。
画完分析！结论写上：
好了，现在是相关性探究，注意标题这么写哈：
好嘞，相关分析就是不同属性的相关系数，相关系数怎么求我简要说以下：
样本点的期望值，怎么理解期望看你自己，我是这么理解的，比如你各科考试是期望成绩X和你对应的概率P，问你问你总科乘积最终期望，那就求和起来~
那么方差呢：
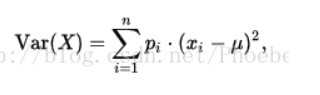
这公式还熟悉吧，u是均值，x是样本点X值，以下把协方差和相关系数都给你吧
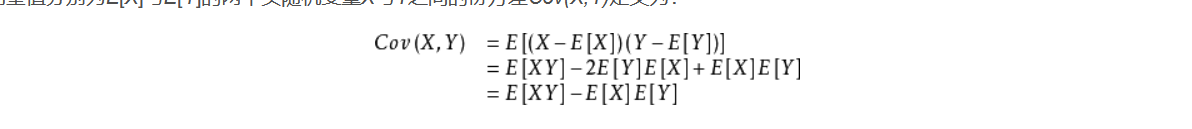
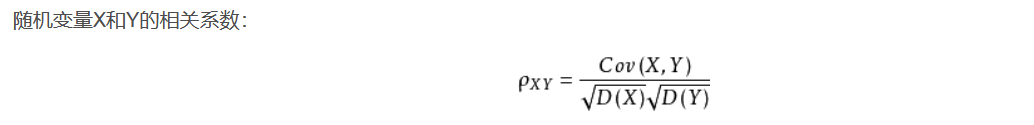
其实这东西我页懵懵懂懂的，协方差大概就是这样：
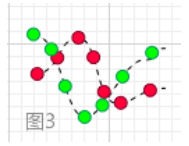
看到了吗，计算两散点图之间的方差距离，这一看，协方差肯定是>0的，如果等于零，两个散点图是重合或平行的。就像这样：
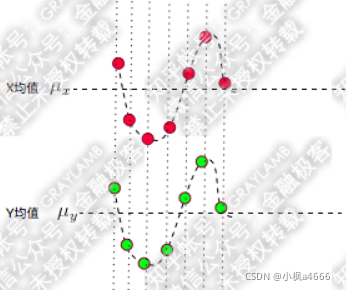
理解了吧，协方差表明了两散点图之间的相关关联度，如果协方差为零，我们就认为他们规律一样，反之，规律差异性很大，甚至不相关。
那么我们为了方便，定义的相关系数就出来啦：
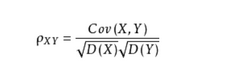
就是这么除的，别问我为什么，总之相关系数取值范围为【-1：1】，越靠近1，越正相关，-1，负相关，0不相关，【-0.6~0.6】相关性很弱，默认没有太大规律。
好嘞，我的论文就直接干公式：
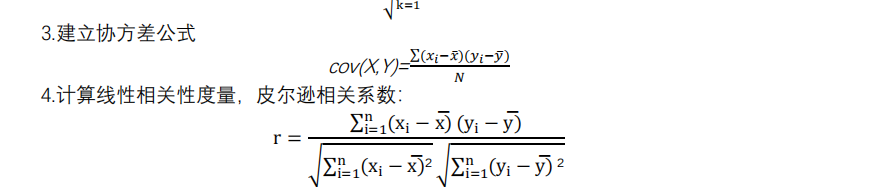然后堆放Python求解的相关系数数据和图：
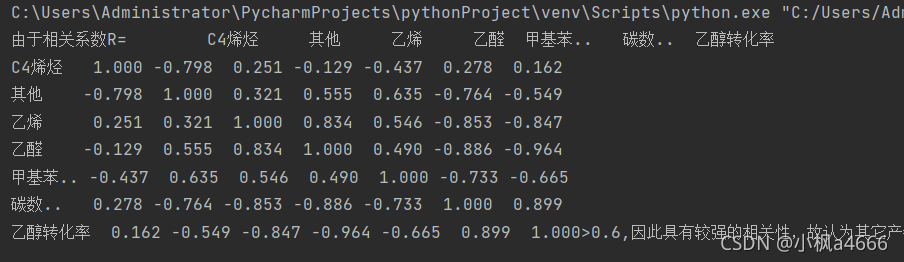
相关系数矩阵：
不用差异，这代码也没几行，因为Python包多，不用我们写，只要会用就行：
这是导入包，不多说了。
df = pd.read_csv('其他产物选择性数据和C4烯烃选择性数据.csv', delimiter=',', encoding='utf-8')
print('由于相关系数R={0}>0.6,因此具有较强的相关性，故认为其它产物与C4烯烃的选择性具有强相关作用，并且为负相关，即为=两者互为拮抗关系'.format(round(df.corr(),3)))
sns.heatmap(df.corr(), xticklabels=df.corr().columns, cmap='RdGy',yticklabels=df.corr().columns, center=0,
annot=True)
plt.show()
看到没，代码核心就这四句话，
1.导入数据，矩阵叫做df
2.打印相关矩阵，df.corr()–计算相关矩阵函数，df指的是矩阵，round（）是保留几位小数函数，这里我保留三位。
3.画相关系数热力图，这没多大讲的，格式是sns.heatmap（待画的矩阵，其他设置原版抄下来也可以不设置） 显示图。plt.show()OK！
好嘞，继续写出你得结论：
好嘞，问题一的求解到此就完全结束了。但是问题一还没完，你需要在模型优缺点那和参考文献以及附录写点东西，这里不多说，直接给你看：
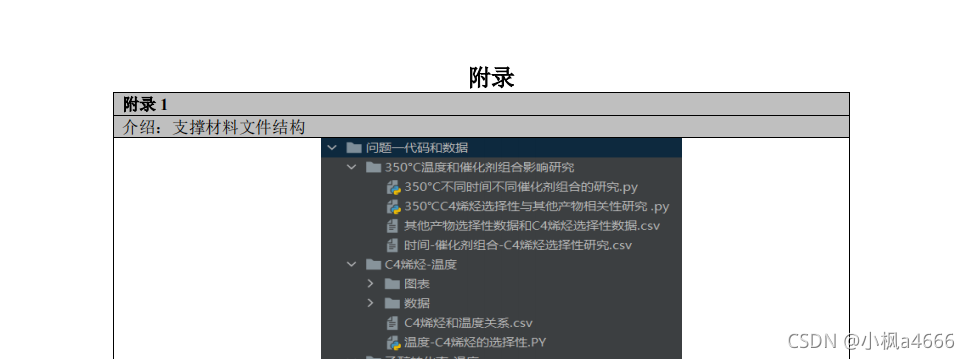
对了，现在你可以很好的写问题一的摘要和分析部分了，因为你得模型都求完了。
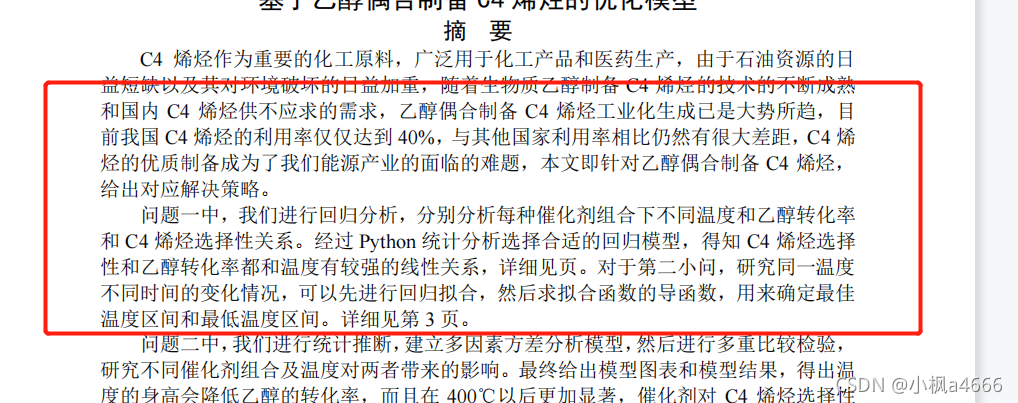
至此，问题一就OK了，你现在得开始问题二了，具体下节课讲了。好好复习吧，多看多写多练！
??????????????????????????????????????????????????????????????????????