开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 人工智能 -> k近邻法算法与模型 -> 正文阅读

[人工智能]k近邻法算法与模型

$k$ 近邻法介绍与算法

参考文献：【KNN算法原理以及代码实现】，【KNN算法原理及实现】，【python 实现KNN算法】

1. 综述

$k$ 近邻法（ $\ neighbor，KNN$ ）是一种基本分类与回归方法。

输入：实例的特征向量，对应于特征空间的点；
输出：实例的类别，可以取多类。

$k$ 近邻法假设给定一个训练数据集，其中的实例类别已定。分类时，对新的实例，根据其 $k$ 最近邻的训练实例的类别，通过多数表决等方式进行预测。
$k$ 近邻法实际上利用训练数据集对特征向量空间进行划分，并作为其分类的”模型“。
k近邻法的三个基本要素：

$k$ 值的选择
距离度量
分类决策规则

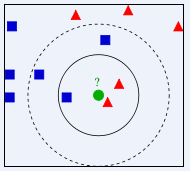
形象解释：
比如一个一定范围的平面随机分布着两种颜色的样本点，在这个平面内有个实例点不知道它是什么颜色，因此通过它周边的不同颜色的点分布情况进行推测，假设取 $k = 3$ ，意思是在离这个实例点最近的样本点中去前三个最近的，然后看这三个当中那种类别占比大，就判断该实例点属于那个类别的，当 $k = 5$ 的时候也一样这样判断，因此 $k$ 的取值很关键，通常不会超过20。当然，因为每个样本有多个特征，因此实际工作中，这个平面就是三维甚至是多维的，道理是一样的。
在这里插入图片描述

2. 算法

$k$ 近邻算法的一大优点是简单、直观：
给定一个训练数据集，对新的输入实例，在训练数据集中找到与该实例最邻近的 $k$ 个实例，这 $k$ 个实例的多数属于某个类，就把该输入实例分为这个类。

2.1 标准解释

输入：训练数据集
$T=\{(x_1,y_1),(x_2,y_2),...,(x_N,y_N)\} \tag 1$

其中， $x_i \in \chi \subseteq R^n$ 为实例的特征向量， $y_i \in \gamma = \{c_1,c_2,...,c_K\}$ 为实例的类别， $i = 1, 2, . . ., N$ ；实例特征向量 $x$ ；

输出：实例 $x$ 所属的类 $y$ 。

根据给定的距离度量，在训练集 $T$ 中找出与 $x$ 最近邻的 $k$ 个点，涵盖这 $k$ 个点的 $x$ 的领域记作 $N_k(x)$ ；
在 $N_k(x)$ 中根据分类决策规则（如多数表决）决定 $x$ 的类别 $y$ ：
$y=\arg \ \max_{c_j} \sum_{x_i \in N_k(x)} I(y_i=c_j),i=1,2,...,N;j=1,2,...,K \tag 2$

式 $(2)$ 中， $I$ 为指示函数，即当 $y_i=c_j$ 时 $I$ 为1，否则 $I$ 为0。
特殊情况：
当 $k = 1$ 的情形，称为最近邻算法。对于输入的实例点（特征向量） $x$ ，最近邻法将训练数据集中与 $x$ 最近邻的类作为 $x$ 的类。

2.2 形象解释

在训练集中数据和标签已知的情况下，输入测试数据，将测试数据的特征与训练集中对应的特征进行相互比较，找到训练集中与之最为相似的前 $K$ 个数据，则该测试数据对应的类别就是 $K$ 个数据中出现次数最多的那个分类，其算法的描述为：

计算测试数据与各个训练数据之间的距离；
按照距离的递增关系进行排序；
选取距离最小的 $K$ 个点；
确定前 $K$ 个点所在类别的出现频率；
返回前 $K$ 个点中出现频率最高的类别作为测试数据的预测分类。

2.3 优缺点以及改进

优缺点：

简单，易于理解，是一个天然的多分类器；
不需要庞大的样本数据也可以完成一个简单的分类；
不需要训练和求解参数（既是优点也是缺点）；
数据量大的时候，计算量也非常大（样本多，特征多）；
不平衡样本处理能力差；
并没有学习和优化的过程，严格来说不算是机器学习。

改进：
进行加权平均，离得近的样本给予更大的权重，离得远的样本使其权重变小。

3. 模型

$k$ 近邻法中，当训练集、距离度量、 $k$ 值及分类决策规则（如多数表决）确定后，对于任何一个新的输入实例，它所属的类唯一地确定。

3.1 距离度量

特征空间中两个实例点的距离是两个实例点相似程度的反映。 $k$ 近邻模型的特征空间一般是 $n$ 维实数向量空间 $R^n$ 。使用的距离欧氏距离，也可以是更一般的 $L_p$ 距离（ $L_p$ distance）或（Minkowski distance）。
设特征空间 $\chi$ 是 $n$ 维实数向量空间 $R^n$ ， $x_i,x_j \in \chi,x_i=(x_i^{(1)},x_i^{(2)},...,x_i^{(n)})^T$ ， $x_j=(x_j^{(1)},x_j^{(2)},...,x_j^{(n)})^T$ ， $x_i,x_j$ 的 $L_p$ 距离定义为：
$L_p(x_i,x_j)=(\sum_{l=1}^{n} |x_i^{(l)}-x_j^{(l)}|^p)^{\frac{1}{p}} \tag 3$
这里 $\geq 1$ 。
当 $p = 2$ 时，称为欧氏距离（Euclidean distance），即：
$L_2(x_i,x_j)=(\sum_{l=1}^{n} |x_i^{(l)}-x_j^{(l)}|^2)^{\frac{1}{2}} \tag 4$
当 $p = 1$ 时，称为曼哈顿距离（Manhattan distance），即：
$L_1(x_i,x_j)=\sum_{l=1}^{n} |x_i^{(l)}-x_j^{(l)}| \tag 5$
当 $p=\infty$ 时，它是各个坐标距离的最大值，即：
$L_{\infty}(x_i,x_j)=\max_{l}|x_i^{(l)}-x_j^{(l)}| \tag 6$
当 $p$ 取不同值时，二维空间中，与原点的 $L_p$ 距离为1（ $L_p=1$ ）的点的图形。

例题：
已知二维空间的3个点 $x_1=(1,1)^T$ ， $x_2=(5,1)^T$ ， $x_3=(4,4)^T$ ，试求在 $p$ 取不同值时， $L_p$ 距离下 $x_1$ 的最近邻点。
解：
因为 $x_1$ 和 $x_2$ 只有第一维的值不同，所以无论 $p$ 取什么值， $L_p(x_1,x_2)=4$ 。而
$L_1(x_1,x_3)=6,L_2(x_1,x_3)=4.24,L_3(x_1,x_3)=3.78,L_4(x_1,x_3)=3.57$
于是得到： $p$ 等于1或2时， $x_2$ 是 $x_1$ 的最近邻点； $p$ 大于等于3时， $x_3$ 是 $x_1$ 的最近邻点。

3.2 $k$ 值的选择

$k$ 值过小，相当于用较小的领域中的训练实例进行预测，”学习“的近似误差会减小，只有与输入实例较近的训练实例才会对预测结果起作用。但缺点是”学习“的估计误差会增大，预测结果会对近邻的实例点非常敏感。如果邻近的实例恰好是噪声，预测就会出错。（ $k$ 值得减小就意味着整体模型变得复杂，容易发生过拟合）。
$k$ 值过大，相当于用较大的领域中的训练实例进行预测，可以减少估计误差，但是缺点是学习的近似误差会增大。这时与输入实例较远的训练实例也会对预测起作用，使预测发生错误。( $k$ 增大，模型会比较简单）。
通常采用交叉验证法来选取最优的 $k$ 值

3.3 分类决策规则

$k$ 近邻法中的分类决策规则往往是多数表决，即由输入实例的 $k$ 个邻近的训练实例中的多数表决决定输入实例的类。
多数表决（majority voting rule）有如下解释：如果分类的损失函数为0-1损失函数，分类函数为：
$\ R^n \rightarrow \{c_1,c_2,...,c_K\} \tag 7$
那么误分类的概率是：
$\not= f(X))=1- P(Y=f(X)) \tag 8$
对于给定的实例 $\in \chi$ ，其最近邻的 $k$ 个训练实例点构成集合 $N_k(x)$ 。如果涵盖 $N_k(x)$ 的区域的类别是 $c_j$ ，那么误分类率是：
$\frac{1}{k} \sum_{x_i \in N_k(x)} I(y_i \not= c_j)=1- \frac{1}{k} \sum_{x_i \in N_k(x)} I(y_i=c_j) \tag 9$
要使误分类最小即经验风险最小，就要使 $\sum_{x_i \in N_k(x)} I(y_i=c_j)$ 最大，所以多数表决规则等价于经验风险最小化。

4. 基于鸢尾花数据集的KNN分类分析

4.1 简介

鸢尾花数据集包括鸢尾花的测量数据（特征属性）以及其所属的类别。
测量数据特征包括: 萼片长度、萼片宽度、花瓣长度、花瓣宽度。
所属类别有三类: Iris Setosa，Iris Versicolour，Iris Virginica ，用数字0,1,2表示。

4.2 导包

import numpy as np
from sklearn import datasets
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import train_test_split

4.3 导入鸢尾花数据

iris = datasets.load_iris()
print('数据量',iris.data.shape)

4.4 拆分数据

拆分属性数据：

iris_X = iris.data

拆分类别数据：

iris_Y = iris.target

拆分数据集为训练集和测试集：
方法一：使用python的train_test_split库进行数据集拆分

iris_X_train , iris_X_test, iris_Y_train ,iris_Y_test = train_test_split(iris_X, iris_Y, test_size=0.2,random_state=0)

使用help(train_test_split)查看详细用法

方法二：随机选择部分数据（20%）作为测试集

np.random.seed(0)
# permutation随机生成0-150的系列
indices = np.random.permutation(len(iris_Y))
iris_X_train = iris_X[indices[:-30]]
iris_Y_train = iris_Y[indices[:-30]]
iris_X_test = iris_X[indices[-30:]]
iris_Y_test = iris_Y[indices[-30:]]

4.5 分类器的初始化

knn = KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',
 metric_params=None, n_jobs=1, n_neighbors=5, p=2,
 weights='uniform')

参数介绍：

n_neighbors=5，就是KNN中的k，默认为5。
weights=‘uniform’，是距离计算中使用的权重，默认为uniform 是等权加权，也可以选distance是按照距离的倒数进行加权，也可以自己设置其他加权方式。（给距离增加权重，如果越近的距离权重越高，能在一定程度上避免样本分布不平均的问题）
metric=‘minkowski’、p=2，表示采用的是欧氏距离的计算。
algorithm=‘auto’，是分类时采取的算法，有brute、kd_tree和ball_tree，三种默认按照数据特征从这三种中选择最合适的。其中kd-tree基于欧氏距离的特性可以快速处理20维以内的数据集，ball_tree基于更一般的距离特性，适合处理高维数据。
leaf_size=30，是kd_tree或ball_tree生成的树的树叶（二叉树中未分枝的节点）的大小。
n_job=1，是并行计算的线程数量，默认是1，输入-1则设为CPU的内核数。

4.6 训练预测

提供数据集进行训练：

knn.fit(iris_X_train,iris_Y_train)

预测测试集数据鸢尾花类型：

predict_result = knn.predict(iris_X_test)
print('预测结果',predict_result)

计算预测的准确率：

print('预测准确率',knn.score(iris_X_test, iris_Y_test))

4.7 训练结果

数据量 (150, 4)
预测结果 [2 1 0 2 0 2 0 1 1 1 2 1 1 1 2 0 1 1 0 0 2 1 0 0 2 0 0 1 1 0]
预测准确率 0.9666666666666667

5. 基于欧式距离的KNN算法及代码分析

5.1 自定义数据及算法

import numpy as np
import operator
import matplotlib.pyplot as plt

def kNN(inX, dataSet, labels, k):
    '''
    kNN算法
    :param inX: 需要分类的数据
    :param dataSet: 样本数据集
    :param labels: 样本数据的标签
    :param k: 需要取出的前k个
    :return: 最有可能的分类
    '''
    # 获取样本数据的个数
    dataSetSize = dataSet.shape[0]
    # np.tile函数将待分类的数据inX"广播"成和样本数据dataSet一样的形状
    # 获取待分类数据inX与样本数据集中的每个数据之间的差
    diffMat = np.tile(inX, (dataSetSize,1)) - dataSet
    # 平方
    sqDiffMat = diffMat**2
    # 按行累加
    sqDistances = sqDiffMat.sum(axis=1)
    # 开方，得出距离（欧氏距离）
    distances = sqDistances**0.5
    # 从小到大排序，得到的是数据的index
    sortedDistIndicies = distances.argsort()
    classCount={}
    # 取出前k个距离最小的
    for i in range(k):
        voteIlabel = labels[sortedDistIndicies[i]]
        # 累计距离出现的次数，并做成字典
        classCount[voteIlabel] = classCount.get(voteIlabel,0) + 1
    # 将字典按值的大小排序,大的在前
    sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1), reverse=True)
    # 返回最有可能的预测值
    return sortedClassCount[0][0]
    
def createDataSet():
    group = np.array([[1.0,1.1],[1.0,1.0],[0,0],[0,0.1]])
    labels = ['A','A','B','B']
    return group, labels
 
if __name__ == '__main__':
    group, labels = createDataSet()
    predict = kNN([0.1,0.1], group, labels, 3)
    print(predict) # 预测结果为B

5.2 改进约会网站的配对效果

数据集介绍：
总共1000条，包含三个特征：

每年获得的飞行常客里程数；
玩视频游戏所耗时间百分比；
每周消费的冰淇淋公升数；

而标签类型为：

1代表“不喜欢的人”
2代表“魅力一般的人”
3代表“极具魅力的人”

代码：

import numpy as np
import pandas as pd
import operator
import matplotlib.pyplot as plt

def file_Matrix(filename):
    '''
    将源数据规整为所需要的数据形状
    :param filename: 源数据
    :return: returnMat:规整好的数据；classLabelVector:数据类标签
    '''
    data = pd.read_csv(filename, sep='\t').as_matrix()
    returnMat = data[:,0:3]
    classLabelVector = data[:,-1]
    return returnMat, classLabelVector
 
def autoNorm(dataSet):
    '''
    数据归一化
    :param dataSet:
    :return:
    '''
    # 每列的最小值
    minVals = dataSet.min(0)
    # 每列的最大值
    maxVals = dataSet.max(0)
    ranges = maxVals - minVals
    # normDataSet = np.zeros(np.shape(dataSet))
    m = dataSet.shape[0]
    # np.tile(minVals,(m,1))的意思是将一行数据广播成m行
    normDataSet = (dataSet - np.tile(minVals, (m,1))) / np.tile(ranges, (m,1))
    # print(normDataSet)
    return normDataSet, ranges, minVals
 
def kNN(inX, dataSet, labels, k):
    '''
    kNN算法
    :param inX: 需要分类的数据
    :param dataSet: 样本数据集
    :param labels: 样本数据的标签
    :param k: 需要取出的前k个
    :return: 最有可能的分类
    '''
    # 获取样本数据的个数
    dataSetSize = dataSet.shape[0]
    # np.tile函数将待分类的数据inX“广播”成和样本数据dataSet一样的形状
    # 获取待分类数据inX与样本数据集中的每个数据之间的差
    diffMat = np.tile(inX, (dataSetSize,1)) - dataSet
    # 平方
    sqDiffMat = diffMat**2
    # 按行累加
    sqDistances = sqDiffMat.sum(axis=1)
    # 开方，得出距离（欧氏距离）
    distances = sqDistances**0.5
    # 从小到大排序，得到的是数据的index
    sortedDistIndicies = distances.argsort()
    classCount={}
    # 取出前k个距离最小的
    for i in range(k):
        voteIlabel = labels[sortedDistIndicies[i]]
        # 累计距离出现的次数，并做成字典
        classCount[voteIlabel] = classCount.get(voteIlabel,0) + 1
    # 将字典按值的大小排序,大的在前
    sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1), reverse=True)
    # 返回最有可能的预测值
    return sortedClassCount[0][0]
 
def datingClassTest():
    hoRatio = 0.10      #hold out 10%
    datingDataMat,datingLabels = file_Matrix('datingTestSet2.txt')       #load data setfrom file
    normMat, ranges, minVals = autoNorm(datingDataMat)
    # print(normMat)
    m = normMat.shape[0]
    numTestVecs = int(m * hoRatio)
    errorCount = 0.0
    for i in range(numTestVecs):
        classifierResult = kNN(normMat[i,:],normMat[numTestVecs:m,:],datingLabels[numTestVecs:m],4)
        print("the classifier came back with: %d, the real answer is: %d" % (classifierResult, datingLabels[i]))
        if (classifierResult != datingLabels[i]): errorCount += 1.0
    print("测试集个数为%d ,分类错误的个数为%d"%(numTestVecs, errorCount))
    print("the total error rate is: %f" % (errorCount/float(numTestVecs)))
    print("accuracy: %f" % ((1-errorCount/float(numTestVecs))*100))
 
if __name__ == '__main__':
    datingClassTest()

训练结果：

the classifier came back with: 2, the real answer is: 2
the classifier came back with: 1, the real answer is: 1
the classifier came back with: 1, the real answer is: 1
the classifier came back with: 1, the real answer is: 1
the classifier came back with: 1, the real answer is: 1
the classifier came back with: 3, the real answer is: 3
the classifier came back with: 3, the real answer is: 3
the classifier came back with: 1, the real answer is: 1
the classifier came back with: 3, the real answer is: 3
the classifier came back with: 1, the real answer is: 1
the classifier came back with: 1, the real answer is: 1
the classifier came back with: 2, the real answer is: 2
the classifier came back with: 1, the real answer is: 1
the classifier came back with: 1, the real answer is: 1
the classifier came back with: 1, the real answer is: 1
the classifier came back with: 1, the real answer is: 1
the classifier came back with: 1, the real answer is: 1
the classifier came back with: 2, the real answer is: 2
the classifier came back with: 3, the real answer is: 3
the classifier came back with: 2, the real answer is: 2
the classifier came back with: 1, the real answer is: 1
the classifier came back with: 2, the real answer is: 2
the classifier came back with: 3, the real answer is: 3
the classifier came back with: 2, the real answer is: 2
the classifier came back with: 3, the real answer is: 3
the classifier came back with: 2, the real answer is: 2
the classifier came back with: 3, the real answer is: 3
the classifier came back with: 2, the real answer is: 2
the classifier came back with: 1, the real answer is: 1
the classifier came back with: 3, the real answer is: 3
the classifier came back with: 1, the real answer is: 1
the classifier came back with: 3, the real answer is: 3
the classifier came back with: 1, the real answer is: 1
the classifier came back with: 2, the real answer is: 2
the classifier came back with: 1, the real answer is: 1
the classifier came back with: 1, the real answer is: 1
the classifier came back with: 2, the real answer is: 2
the classifier came back with: 3, the real answer is: 3
the classifier came back with: 3, the real answer is: 3
the classifier came back with: 1, the real answer is: 1
the classifier came back with: 2, the real answer is: 2
the classifier came back with: 3, the real answer is: 3
the classifier came back with: 3, the real answer is: 3
the classifier came back with: 3, the real answer is: 3
the classifier came back with: 1, the real answer is: 1
the classifier came back with: 1, the real answer is: 1
the classifier came back with: 1, the real answer is: 1
the classifier came back with: 1, the real answer is: 1
the classifier came back with: 2, the real answer is: 2
the classifier came back with: 2, the real answer is: 2
the classifier came back with: 1, the real answer is: 1
the classifier came back with: 3, the real answer is: 3
the classifier came back with: 2, the real answer is: 2
the classifier came back with: 2, the real answer is: 2
the classifier came back with: 2, the real answer is: 2
the classifier came back with: 2, the real answer is: 2
the classifier came back with: 3, the real answer is: 3
the classifier came back with: 1, the real answer is: 1
the classifier came back with: 2, the real answer is: 2
the classifier came back with: 1, the real answer is: 1
the classifier came back with: 2, the real answer is: 2
the classifier came back with: 2, the real answer is: 2
the classifier came back with: 2, the real answer is: 2
the classifier came back with: 2, the real answer is: 2
the classifier came back with: 2, the real answer is: 2
the classifier came back with: 3, the real answer is: 3
the classifier came back with: 2, the real answer is: 2
the classifier came back with: 3, the real answer is: 3
the classifier came back with: 1, the real answer is: 1
the classifier came back with: 2, the real answer is: 2
the classifier came back with: 3, the real answer is: 3
the classifier came back with: 2, the real answer is: 2
the classifier came back with: 2, the real answer is: 2
the classifier came back with: 3, the real answer is: 1
the classifier came back with: 3, the real answer is: 3
the classifier came back with: 1, the real answer is: 1
the classifier came back with: 1, the real answer is: 1
the classifier came back with: 3, the real answer is: 3
the classifier came back with: 3, the real answer is: 3
the classifier came back with: 1, the real answer is: 1
the classifier came back with: 2, the real answer is: 2
the classifier came back with: 3, the real answer is: 3
the classifier came back with: 3, the real answer is: 1
the classifier came back with: 3, the real answer is: 3
the classifier came back with: 1, the real answer is: 1
the classifier came back with: 2, the real answer is: 2
the classifier came back with: 2, the real answer is: 2
the classifier came back with: 1, the real answer is: 1
the classifier came back with: 1, the real answer is: 1
the classifier came back with: 3, the real answer is: 3
the classifier came back with: 2, the real answer is: 3
the classifier came back with: 1, the real answer is: 1
the classifier came back with: 2, the real answer is: 2
the classifier came back with: 1, the real answer is: 1
the classifier came back with: 3, the real answer is: 3
the classifier came back with: 3, the real answer is: 3
the classifier came back with: 2, the real answer is: 2
the classifier came back with: 2, the real answer is: 1
the classifier came back with: 1, the real answer is: 1
测试集个数为99 ,分类错误的个数为4
the total error rate is: 0.040404
accuracy: 95.959596