[人工智能]深度学习(DL)-2.1 深度学习实战技巧——网络正则化、归一化、参数初始化 (Practical aspects of Deep Learning)

1.深度学习实战

1.1 开发流程与需要考虑的问题

开发流程：
?是一个迭代循环过程：提出想法->编写代码->进行实验验证->提出新想法->重写代码->再次实验验证->…
?
需要考虑的问题：

• 网络层数
• 神经元单元数
• 学习率
• 激活函数选择
• …

1.2 数据集划分

1.2.1 三种数据集

训练集 (train set)：用来训练模型
验证集 (valid/dev set)：用于验证超参数选择，以此选出最好模型 (非必须)
测试集 (test set)：用于模拟真实情况，对模型进行无偏估计，评价模型

1.2.2 数据集划分原则

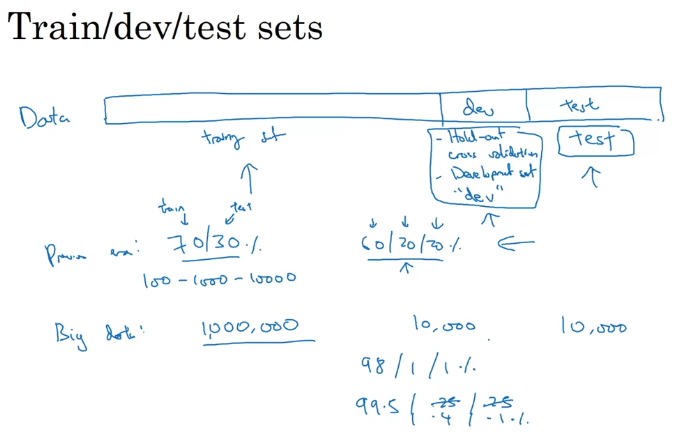
数据量较少时：
如100、1000、10000的数据量大小
无验证集：70% / 30%，来划分训练集和测试集
有验证集：60% / 20% / 20%，来划分训练集、验证集、测试集

数据量较大时：
百万级数据量，无固定原则，根据具体问题而定，通常：
百万数据量：98% / 1% / 1%
超百万数据量：99.5% / 0.25% / 0.25%（或者99.5% / 0.4% / 0.1%）

1.2.3 数据集分布

同分布原则： 确保训练集与测试集有相同分布
原因： 若分布不同，则训练出的模型表现与真实情况不符，在训练集/测试集上表现良好，但在测试集/实际使用时效果很差
例子：
?训练集上使用网络上收集的猫猫图片训练模型；测试集使用用户自己拍摄的猫猫图片
?由于网上收集的图片与用户自己拍摄的照片并不一样，存在数据集分布不匹配问题

1.3 偏差与方差

1.3.1 基本概念

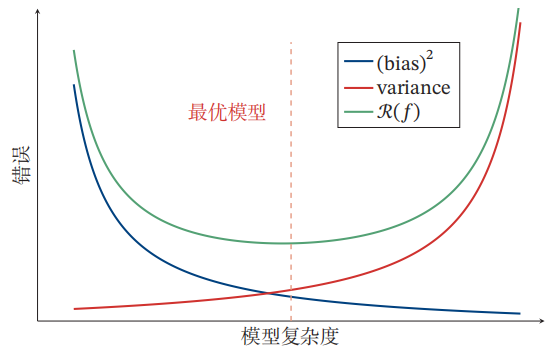
原因 : 为了避免过拟合，需要权衡模型的拟合能力和复杂度；
???复杂度高的模型拟合能力强，但容易过拟合；
???复杂度低的模型拟合能力弱，不易过拟合，但容易欠拟合
功能 : 通过对偏差与方差进行分析，能较准确发现模型问题所在，从而对模型进行调整
定义 :

• 偏差(Bias)：指模型在不同训练集上的平均性能和最优模型的差异，用来衡量模型的拟合能力
• 方差(Variance)：指模型在不同训练集上的差异，用来衡量是否过拟合

数学原理(选修)：
假设样本真实分布为$p_r(x,y)$，使用平方损失函数，则模型$f(x)$的期望错误为：
$$R(f)=E_{(x,y)～p_r(x,y)}[(y?f(x{)}^2)]$$
最优模型为：
$$f^{?}(x)=E_{y～p_r(y|x)}[y]$$
其中$p_r(y|x)$为样本的真实条件分布，$f^{?}(x)$为最优模型，其损失为：
$$?=E_{(x,y)～p_r(x,y)}[(y?f^{?}(x){)}^2]$$
而损失$?$通常由样本分布及噪音引起，无法通过优化模型来减少，因此期望错误可分解为：
$$\begin{gathered} R(f)=E_{y～p_r(y|x)}[(y?f^{?}(x)+f^{?}(x)?f(x){)}^2] \\ =E_{x～p_r(x)}[(f(x)?f^{?}(x){)}^2]+? \end{gathered}$$
其中，第一项是当前模型和最优模型的差距，是机器学习算法可以优化的目标
而实际训练时，训练集$D$是从真实分布$p_r(x,y)$上独立同分布采样出的有限集合，不同的训练集会得到不同的模型。令$f_D(x)$表示在训练集$D$上学习到的模型。
对于单个样本$x$，从不同训练集$D$得到的模型$f_D(x)$与最优模型$f^{?}(x)$的期望差距为：
??????????????????
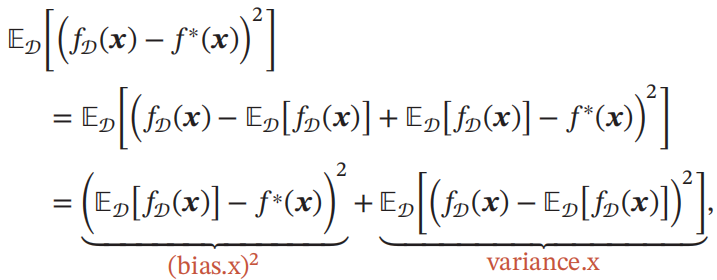
其中第一项即为偏差，而第二项即为方差
扩展到全部训练集上，即得到整个数据集上的方差与偏差公式：
??????????????????

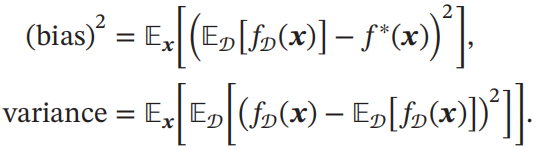
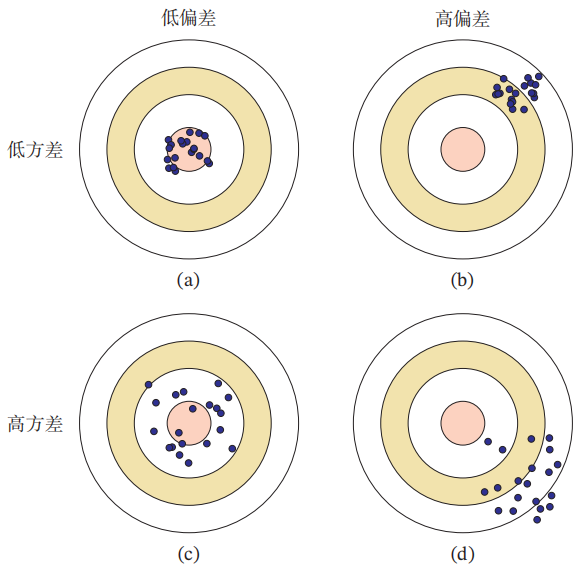
1.3.2 四种情况

四种情况与分析：

• 高方差&低偏差：训练集上表现好，测试集上表现差；泛化能力差，拟合能力强；过拟合
• 高偏差&低方差：训练集上表现差，测试集上表现更差；泛化能力好，拟合能力不足；欠拟合
• 高偏差&高方差：训练集和测试集上表现都很差；最坏情况，整体欠拟合，但又对部分错误情况过拟合
• 低偏差&低方差：训练集和测试集上表现都很好；完美模型
  
  

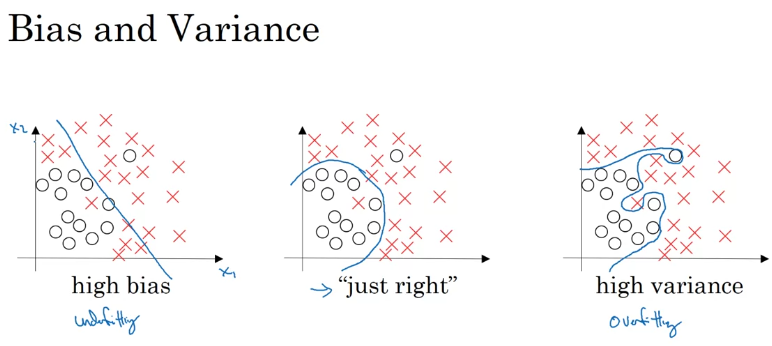
方差与偏差平衡：

1.3.3 解决方法

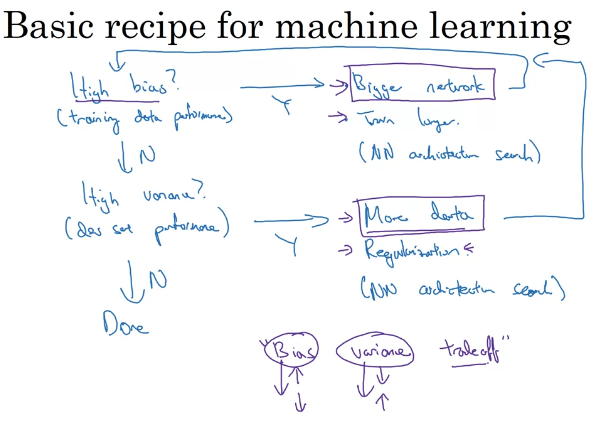
高偏差：更大网络、更长训练时间、其他网络结构
高方差：更多数据、正则化、其他网络结构

2.网络正则化(Network Regularization)

2.1 基本概念

定义： 是一类通过限制模型复杂度，从而避免过拟合，提高泛化能力的方法，解决高方差问题；比如引入约束、增加先验、提前停止等
原因： 由于神经网络拟合能力很强，若不加限制很容易过拟合，因此需要正则化来限制模型，提高其泛化能力

2.2 L1和L2正则化

概述： L1与L2正则化是最常用的方法，通过约束参数的L1和L2范数来减小模型在训练集上的过拟合现象
范数： 是一个表示向量“长度”的函数，为向量空间内的所有向量赋
予非零的正长度或大小

• Lp范数：$l_p(v)\equiv ||v|{|}_p=({\sum }_{n=1}^N|v_n{|}^p{)}^{1/p}$
• L1范数：$||v|{|}_1={\sum }_{n=1}^N|v_n|$
  由于L1范数在零点不可导，可用下式代替：
  ????$||v|{|}_1={\sum }_{n=1}^N\sqrt{v^2+?}$
• L2范数：$||v|{|}_2=\sqrt{{\sum }_{n=1}^N{v}_n^2}=\sqrt{v^{T}v}$

L1正则化： 即在代价函数中加入L1范数，以逻辑回归为例
$$J(w,b)=\frac{1}{m}\sum _{i=1}^{m}l({\hat{y}}^i,y^i)+\frac{\lambda }{2m}\sum _{j=1}^n|w_j|$$
L2正则化： 即在代价函数中加入L2范数，以逻辑回归为例
$$J(w,b)=\frac{1}{m}\sum _{i=1}^{m}l({\hat{y}}^i,y^i)+\frac{\lambda }{2m}\sum _{j=1}^n{w}_j^2$$
原理：

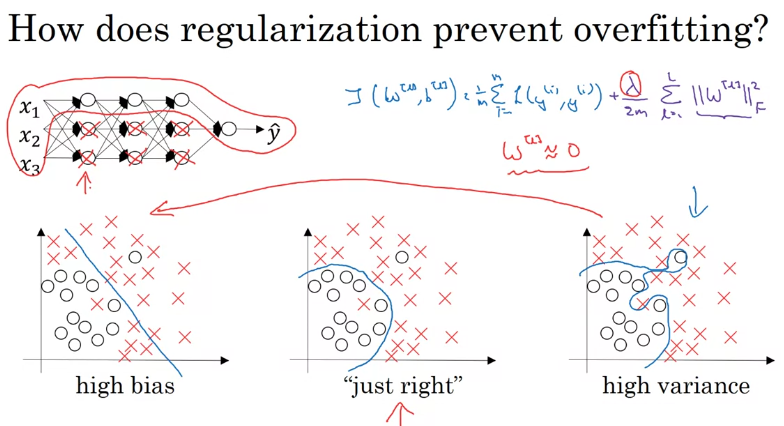
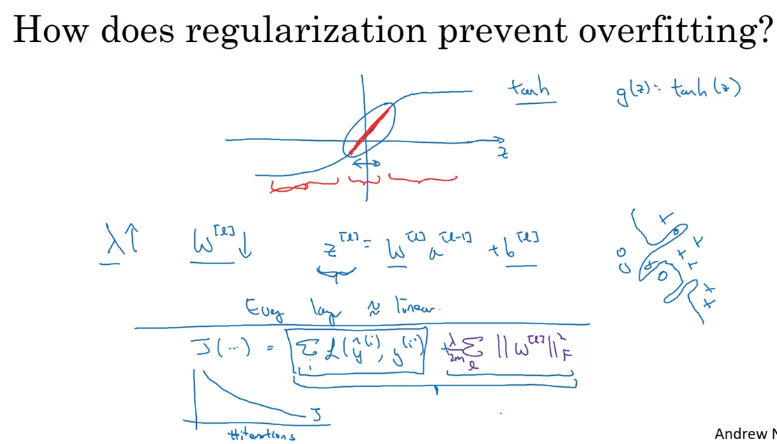
(1)使权值w减少，从而使一些神经元权值近似为0，相当于删去了一些神经元，简化网络，缓解过拟合

例：假设$\lambda$设为很大，则代价函数值几乎只与权重$w$有关，此时为了减少损失值，则需要减少$w$的值，相当于删除一些神经元，简化网络结构
?
(2)使权值w减少，则神经元输出$Z$更易落在激活函数中间部分，防止激活函数值过大，出现梯度消失问题，提高训练速度
?

数学原理(选修)：
通过引入L1和L2正则化，优化问题可写为：
$${\theta }^{?}=arg\underset{\theta }{m}in\frac{1}{N}\sum _{n=1}^{N}L(y^{(n)},f(x^{(n)};\theta ))+\lambda l_p(\theta )$$
其中$L(?)$为损失函数，$N$为训练样本数量，$f(?)$为神经网络，$\theta$为其参数，$l_p$为范数，$p$通常取值为 { 1 , 2 } \{1,2\} {1,2}，表示L1范数和L2范数，$\lambda$为正则化系数
由此，带正则化的优化问题等价于带条件约束的优化问题：
??????????????????
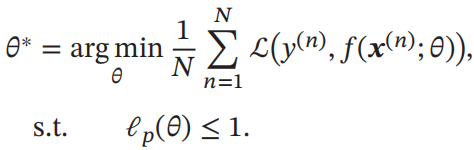
此时，不同约束条件下的最优化问题可用下图表示：
????????
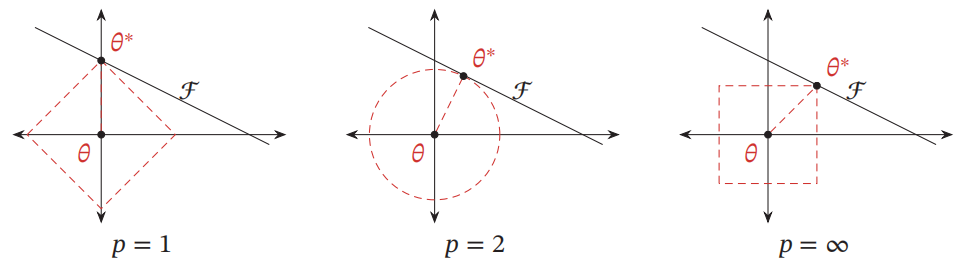
红色线表示函数$l_p=1$，$F$为函数$f(\theta )$的等高线。可以看出，通过范数的约束，模型目标函数的形状被改变，最优解会被限制在坐标轴上，使得最终的向量为稀疏性向量，更加容易训练

2.3 权值衰减(Weight Decay)

概述： 是一种有效的正则化方法，在每次参数更像时，引入一个衰减系数，防止权值过大发生过拟合
公式：
$${\theta }_t=(1?\beta ){\theta }_{t?1}?\alpha g_t$$
其中，$g_t$表示第t步时的梯度，$\alpha$为学习率，$\beta$为权重衰减系数，通常取较小值，如0.0005.

与L2正则化关系：
在标准随机梯度下降中，权重衰减与L2正则化效果相同，而较复杂优化算法中(如Adam)，两者不等价
原理：
使用L2正则化后，其梯度变为：
$$d{W}^{[l]}=(form\_backprop)+\frac{\lambda }{m}{W}^{[l]}$$
则梯度更新公式变为：
$$W^{[l]}=W^{[l]}?\alpha d{W}^{[l]}=(1?\frac{\alpha \lambda }{m}{W}^{[l]})?\alpha (form\_backprop)$$
其中，$(1?\frac{\alpha \lambda }{m})$为小于1的值，因此会使权重变小，等价于权重衰减

2.4 提前停止(Early Stop)

定义： 一种简单有效的方法，当验证集上的损失值不再下降时，就停止迭代

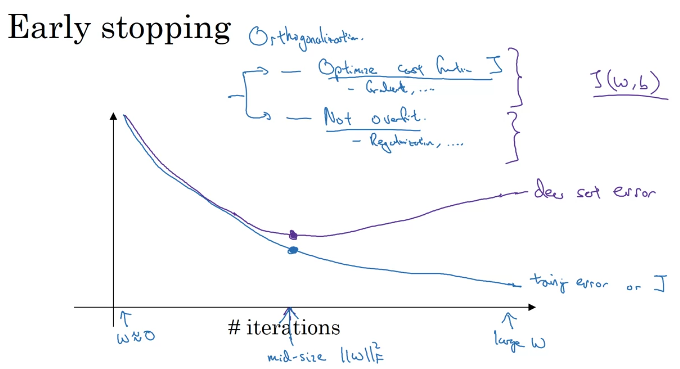
缺点： 虽然避免了过拟合，但同时也停止了对模型优化，可能无法得到最优模型

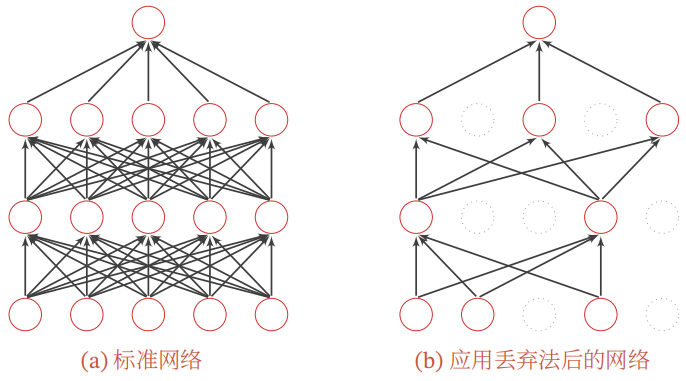
2.5 丢弃法(Dropout)

定义： 在训练时，以一定概率随机丢弃部分神经元(及其对应边)，以此避免过拟合
?
实现：
设置一个固定的概率 $p$．对每一个神经元都以概率 $p$ 来判定要不要保留．对于一个神经层$\mathbf{y}=f(\mathbf{W}\mathbf{x}+\mathbf{b})$，我们可以引入一个掩蔽函数$mask(?)$ 使得$\mathbf{y}=f(\mathbf{W}mask(\mathbf{x})+\mathbf{b})$．掩蔽函数$mask(?)$的定义为：
????????????????
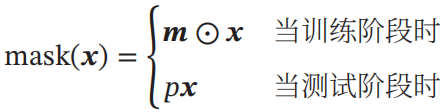
其中 𝒎 ∈ { 0 , 1 } D 𝒎 ∈ \{0, 1\}^D m∈{0,1}D 是丢弃掩码(Dropout Mask)，通过以概率为$p$的伯努利分布随机生成，$D$ 为输入$\mathbf{x}$的维度

权重复现：
在训练时，激活神经元的平均数量为原来的$p$倍．而在测试时，所有的神经元都是可以激活的，这会造成训练和测试时网络的输出不一致．为了缓解这个问题，在测试时需要将神经层的输入$\mathbf{x}$乘以$p$，也相当于把不同的神经网络做了平均

原理：
使神经元不依赖于某一特定特征，而是考虑所有特征；因为神经元会被随机丢弃，若只依赖与某一特征，当该神经元被丢弃时，模型表现会大幅度下降
使每个神经元更努力的学习，只依靠自己，避免”偷懒“；因为其他神经元随时可能被丢弃，是不可靠的，因此只能尽可能提高自身表现

数学原理(选修)
集成学习角度：每次丢弃就相当于采样出一个自网络，丢弃$N$次则有$2^N$个子网络，每次迭代都相当于对子网络进行训练，且这些子网络共享参数，最终的网络就相当于集成了$2^N$个子网络的组合模型

贝叶斯学习角度：用$y=f(x;\theta )$表示神经网络，贝叶斯学习是假设参数$\theta$为随机向量，并且先验分布为$q(\theta )$，贝叶斯方法的预测为：
????????????
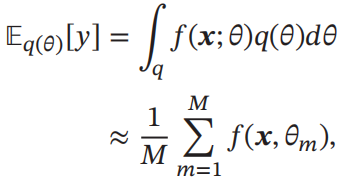
其中$f(\mathbf{x},\theta m)$为第𝑚次应用丢弃方法后的网络，其参数𝜃𝑚 为对全部参数𝜃 的一次采样

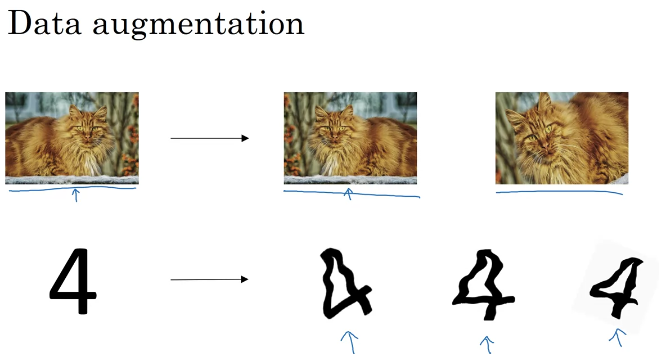
2.6 数据增强(Data Augmentation)

定义： 对原训练数据进行一些处理变化，从而得到更多训练数据，且能提高模型鲁棒性，避免过拟合
??
原理： 能成倍增加训练数据量，使模型训练更充分，更具鲁棒性
数据增强方法：

• 旋转：将图像顺时针或逆时针旋转一定角度
• 翻转：将图像沿水平或垂直方法随机翻转一定角度
• 缩放：将图像放大或缩小一定比例
• 平移：将图像沿水平或垂直方法平移一定步长
• 加噪声：加入随机噪声

2.7 标签平滑

定义： 向输出标签中加入噪声，从而避免模型过拟合
原理： 若训练数据中存在错误标注的标签，当模型对这些错误标签进行学习时，将导致过拟合，向标签中加入噪音以平滑各样本对模型的影响(相当于对标签均值化)，从而缓解因错误标签而造成的过拟合
数学原理(选修)：
?设一个样本$x$的白哦去用如下one-hot向量表示：
$$y=[0,...,0,1,0,...,0{]}^T$$
?此时若使用Softmax分类器与交叉熵损失函数，最小化损失函数即使正确类与其他类的权重差异变大，要使某一类输出概率接近1，则其得分要远大于其他类的得分，导致其权重越来越大，若该标签是错误的，则会对错误标签出现严重过拟合。通过向标签中加入噪音进行平滑，就可以缓解这种问题
?设样本以$?$的概率为其他类，则平滑后的标签为：
$$\tilde{y}=[\frac{?}{K?1},...,\frac{?}{K?1},1??,\frac{?}{K?1},...,\frac{?}{K?1}{]}^T$$
?其中，K为标签的数量，这样就使得各类别的标签值差距缩小，即使对错误标签进行优化也不会带来严重影响，并且通常不会损害模型分类能力

3.归一化(Normalization)

3.1 基本概念

定义： 泛指把数据特征转换为相同尺度的方法，比如把数据特征映射到[0, 1]或[?1, 1]区间内，或者映射为服从均值为0、方差为1的标准正态分布，从而消除量纲的影响
?

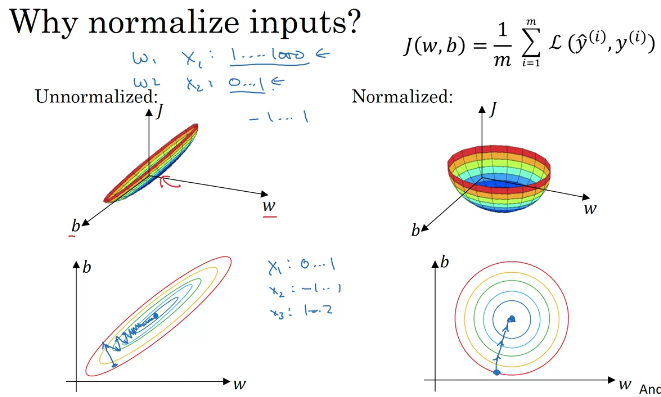
原理： 不同特征具有不同的单位，设一特征A以"米”为单位，另一特征B以"厘米"为单位，那么B的值将为A的100倍，在训练时B对模型的影响要远大于A，这显然是不合理的。因此需要将各维度的特征转换到相同的取值区间中，消除量纲(单位)的影响
功能：
?(1)消除量纲影响，使模型平等对待各特征
?(2)改变优化问题在向量空间中的图形，使模型训练速度更快
?

3.2 常用方法

3.2.1 最小最大值归一化 (Min-Max Normalization)

定义： 将各特征取值归一至[0,1]或[-1,1]，其公式如下：
???????????
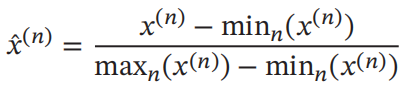
其中，n表示有n个样本，${\hat{x}}^{(n)}$为每一维特征$x$归一化后特征，min($x$)和max($x$)为特征$x$在全部样本中的最小值和最大值

3.2.2 标准化 (Standardization)

定义： 又叫做Z值归一化(Z-Score Normalization)，将每一维特征都变为均值为0，方差为1的标准正太分布，其公式如下：
$${\hat{x}}^{(n)}=\frac{x^{(n)}?\mu }{\sigma }$$
其中，$\mu$为特征$x$的均值，$\sigma$为标准差

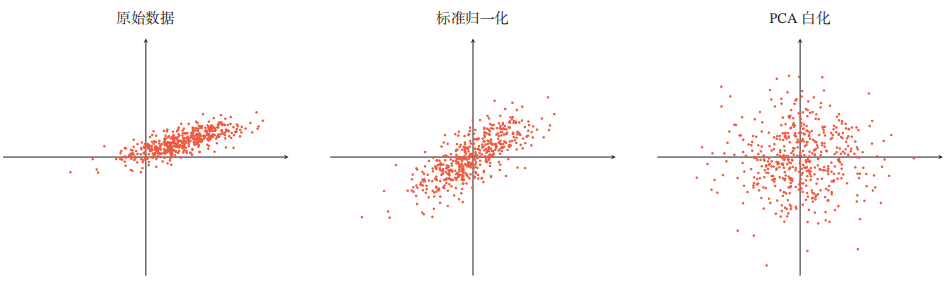
3.2.3 白化 (Whitening)

定义： 能降低输入特征间的冗余性，经过白化处理后的特征间相关性较低，所有特征具有相同的方差。一种主要的实现方法是用主成分分析(PCA)消除各特征间的相关性
效果：
?

4. 参数初始化

4.1 基本概念

概述： 神经网络的参数学习是一个非凸优化问题，当使用梯度下降法来进行优化网络参数时，参数初始值的选取十分关键，关系到网络的优化效率和泛化能力
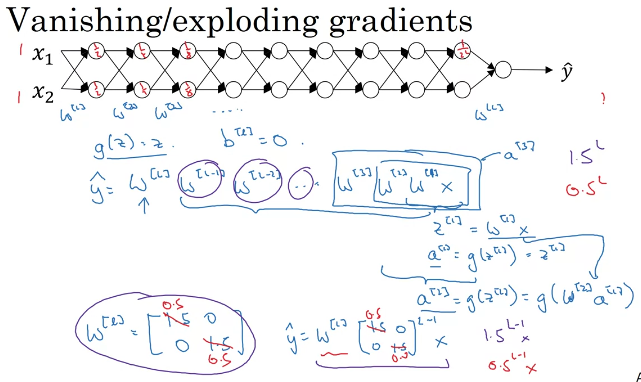
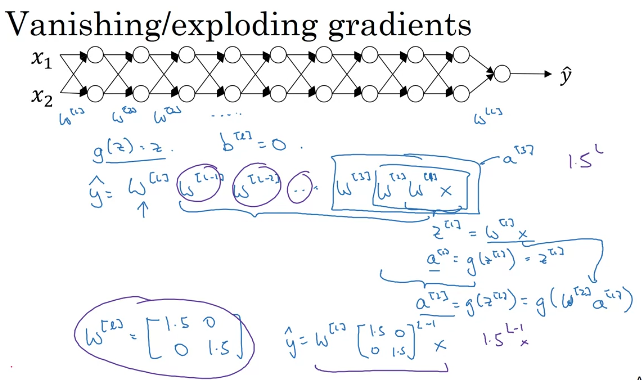
功能： 使权重不会增加/减小过快，缓解梯度消失/梯度爆炸问题
两大问题——梯度消失与梯度爆炸：

• 梯度消失：网络最终输出$\hat{y}$通过之前层结果不断累乘得到，与神经网络层数呈指数关系，若权值小于1，则值会不断减小，最终几乎消失
  ?
• 梯度爆炸：同理，由于权值与层数呈指数关系，若权值大于1，则最终结果可能非常大
  ?

4.2 三种初始化类型

4.2.1 随机初始化

定义： 将各参数初始化为某一范围内的随机数，是最为常用的方法
功能： 由于将权值初始化为0会出现对称权重现象，导致模型失效，因此随机初始化最为常用，能使不同神经元间区分度更好

4.2.2 固定值初始化

定义： 对于某些特殊参数，可以用固定值来初始化，如偏置(Bias)通常用0来初始化，但在LSTM遗忘门中通常初始化为1或2
功能： 针对不同模型进行专门优化，能提高模型效果，但并不是普遍方法

4.2.3 预训练初始化

定义： 使用预先训练好的模型参数作为初始参数，并对当前模型继续训练进行精调
功能： 能极大提高模型训练速度与效果，在有预训练模型的任务中被广泛使用，如BERT

4.3 常用随机初始化方法

4.3.1 基于固定方差初始化

定义： 从一个固定均值和方差的分布中采样生成参数初始值
常用分布：
?高斯分布：使用高斯分布$N(0,{\sigma }^2)$对参数初始化
?均匀分布：从给定区间$[?r,r]$内用均匀分布初始化参数
问题： 对固定方差值的选择很重要，过小/过大都可能导致梯度消失/爆炸

4.3.2 基于方差缩放的参数初始化

定义： 为尽可能保持各神经元输入和输出的方差一致，根据神经元连接数量来自适应调整初始化分布的方差
功能： 能根据网络结构的不同自适应设置初始化参数，根据神经元性质进行差异化设置，能缓解梯度消失或梯度爆炸
原理： 一个神经元的输入连接越多，其每个输入连接上的权重就应该越小，以避免神经元输出过大，导致落在激活函数远端，引起梯度消失(Sigmoid函数为激活函数时)
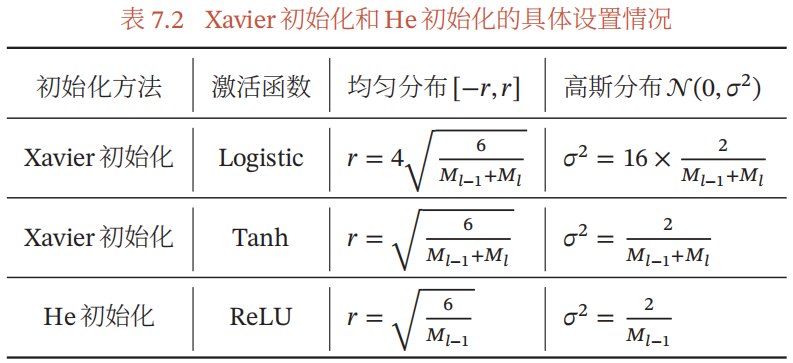
常用方法：Xavier初始化与He初始化
其对应不同激活函数的初始化设置如下图：
??

4.3.3 正交初始化

原因：上述两种基于方差的方法都是对每个参数进行独立采样，由于采样的随机性，最终采样出的权重矩阵可能仍存在梯度消失或梯度爆炸问题，因此需要一种具有范数保持性的方法
定义：将参数矩阵$W^{(l)}$初始化为正交矩阵，即$W^{(l)}(W^{(l)}{)}^T=I$
功能：使误差项在反向传播中具有范数保持性，能避免梯度消失或梯度爆炸
实现：
?(1)用均值为0、方差为1的高斯分布初始化一个矩阵
?(2)对该矩阵进行奇异值分解，得到两个正交矩阵，使用其中一个作为权重矩阵

5.梯度检验

5.1 梯度的近似计算

两种近似计算方法：
(1)双边导数：
$$f^{\prime }(\theta )=\frac{f(\theta +\epsilon )?f(\theta ?\epsilon )}{2\epsilon }$$
??其误差为$O({\epsilon }^2)$
(2)单边导数：
$$f^{\prime }(\theta )=\frac{f(\theta +\epsilon )?(\theta )}{\epsilon }$$
??其误差为$O(\epsilon )$
通常使用双边导数来近似计算梯度，因为其精度更高

例：
使用双边导数近似计算梯度，假设误差项$\epsilon =0.01$，参数值$\theta =1$，则近似梯度为：
$$g(\theta )\approx \frac{(1+0.01)?(1?0.01)}{2?(0.01)}=3.0001\approx 3$$

5.2 基本概念与实现

定义： 为了快速判断模型是否搭建正确，通常进行梯度检验，通过手动计算出近似梯度与模型计算出的梯度进行比较，来检验梯度下降是否正确
方法：
?(1)将各参数合成一个为向量$\theta$，将各参数的偏导数合成一个为另一个向量$d\theta$
??
?(2)计算近似梯度，并计算近似梯度与真实梯度的欧式距离，两者相近则正确，相差较大则存在问题
??

5.3 注意事项

进行梯度检验时，应注意：

• 不要在训练过程中使用，只在debug时用
• 如果未通过梯度检验，则应检查每个参数，看是具体哪几个值差距很大
• 不要忘记使用正则化
• 在使用dropout时，无法进行梯度检验
• 在初始化参数后进行梯度检验，在模型训练一段时间后再次进行梯度检验
  

内容汇总：Coursera深度学习(DL)专项课-课程笔记与编程实战-汇总