李宏毅深度学习2021春p5-9:神经网络训练技巧
训练遇到的问题
- 参数不断的更新,training loss一开始下降,然后不会再下降,但距离0还有很远的gap;
- 一开始model就train不起来,不管怎么update参数,loss一直比较大。
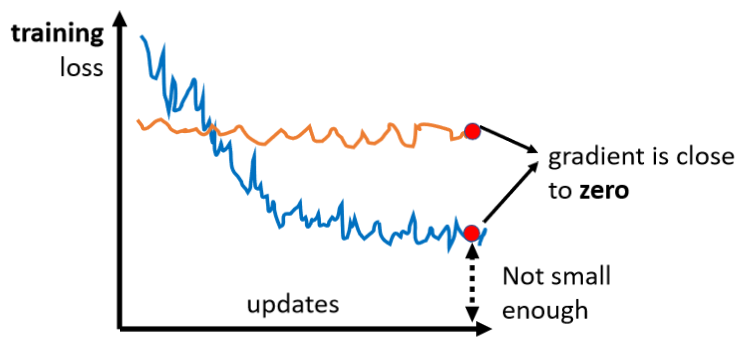
导致上述问题的原因可能有很多,我们先回忆一下梯度下降算法在现实世界中面临的挑战:
- 问题1:局部最优(Stuck at local minima)
- 问题2:等于0(Stuck at saddle point)
- 问题3:趋近于0(Very slow at the plateau)
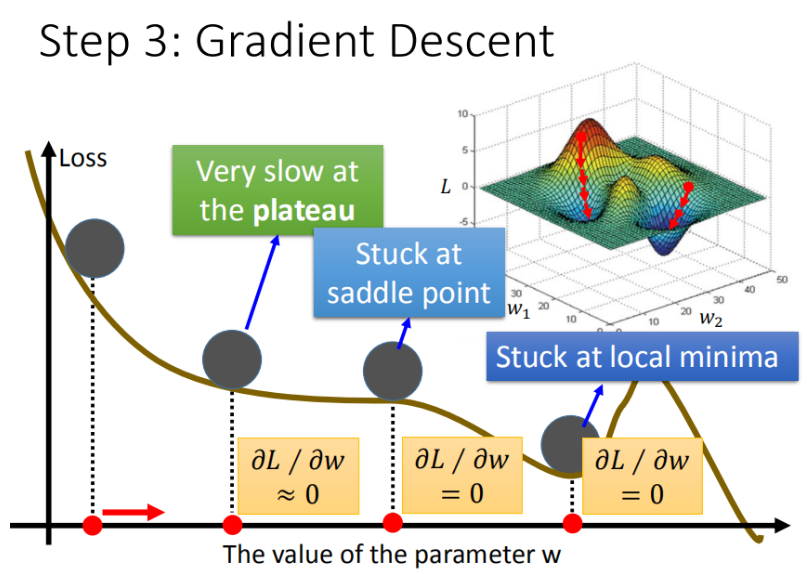
像这种gradient为0的点,统称critical point,我们先从问题1和问题2来看看如何“炼丹”。
局部最小值local minima和鞍点saddle point
Critical Point
gradient为0的点。
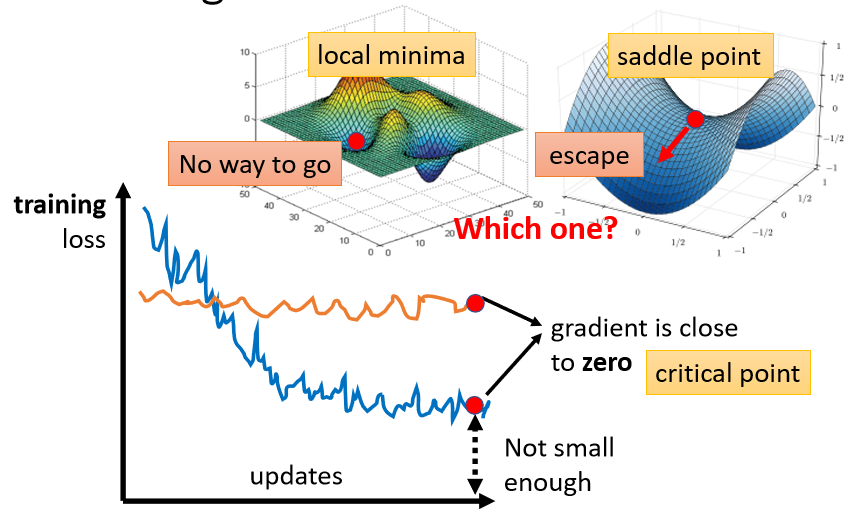
local minima
**现在所在的位置已经是局部loss最低的点,**往四周走 loss都会比较高,可能没有路可以走。
saddle point
**saddle point从某个方向还是有可能到达loss更低的位置,**只要逃离saddle point,就有可能让loss更低。
如何判断某个位置是local minima还是saddle point?
通过泰勒级数展开估计(Tayler Series Approximation)loss function的形状。
也就是,虽然无法完整、准确写出 L ( θ ) L(\theta) L(θ),但如果给定某一组参数 θ ′ \theta' θ′,在 θ ′ \theta' θ′附近的loss function可以通过泰勒级数展开来估计:
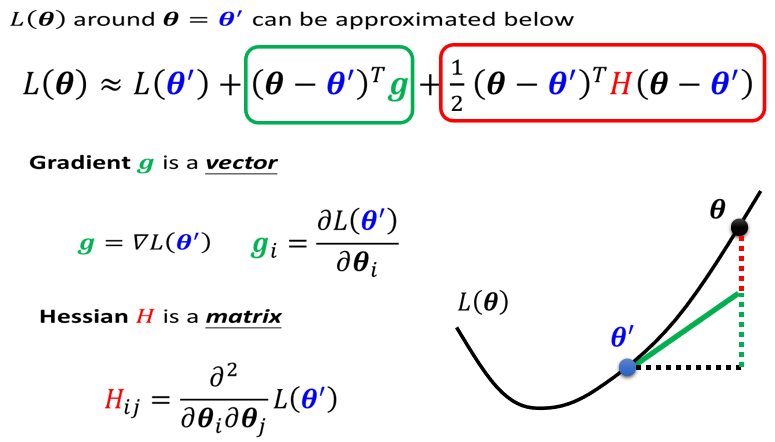
- 第一项 L ( θ ′ ) L(\theta') L(θ′):当 θ \theta θ跟 θ ′ \theta' θ′很近的时候, L ( θ ) L(\theta) L(θ)跟 L ( θ ′ ) L(\theta') L(θ′)比较靠近,但还有一些差距;
- 第二项 ( θ ? θ ′ ) T g (\theta-\theta')^Tg (θ?θ′)Tg:是一个向量,这个 g g g是gradient,这个gradient会来弥补 θ ′ \theta' θ′跟 θ \theta θ之间的差距。有时候gradient会写成 ? L ( θ ′ ) \nabla L(\theta') ?L(θ′),它的第 i i i个component,就是 θ θ θ的第 i i i个component对 L L L的微分,加上这一项之后仍然还有差距;
- 第三项中 ( θ ? θ ′ ) T H ( θ ? θ ′ ) (\theta-\theta')^TH(\theta-\theta') (θ?θ′)TH(θ?θ′):其中 H H H跟Hessian有关,是一个矩阵,第三项会再补足与真正的L(θ)之间的差距。 H H H是L的二次微分构成的矩阵,它第 i i i个row,第 j j j个column的值 H i j H_{ij} Hij?,是把 θ θ θ的第 i i i个component,对 L L L作微分,再把 θ θ θ的第 j j j个component,对 L L L作微分,也就是做两次微分以后的结果 。
总的来说, L ( θ ) L(\theta) L(θ)跟两个东西有关,跟gradient有关,跟hessian有关。gradient就是一次微分,hessian是内含二次微分的项目。
如果我们今天走到了一个critical point,意味着上式中 g = 0 g=0 g=0,只剩下 L ( θ ′ ) L(\theta') L(θ′)和红色的这一项:
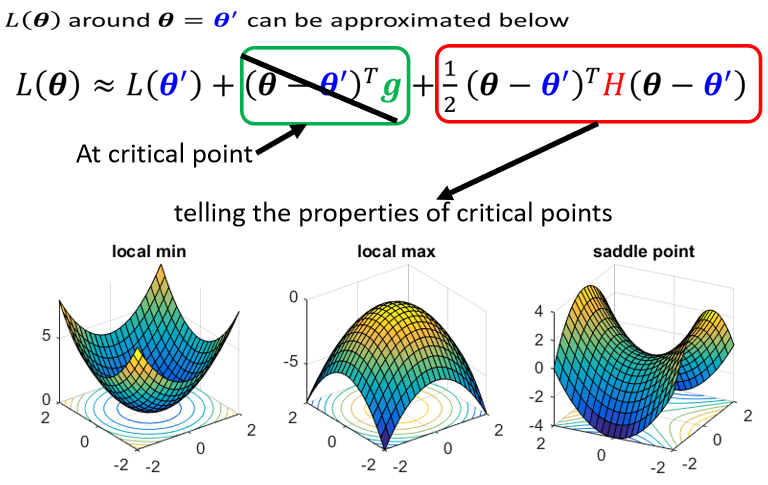
于是可以通过红色这一项判断 θ ′ \theta' θ′附近的error surface长什么样,从而判断现在是在local minima、local max还是saddle point。
通过Hession矩阵判断 θ ′ \theta' θ′附近的error surface
把 ( θ ? θ ′ ) (\theta-\theta') (θ?θ′)用向量 v v v来表示,根据 v T H v v^THv vTHv的值来判断:

线性代数中,如果所有的 v v v带入 v T H v v^THv vTHv的值都大於零,那 H H H叫做positive definite 正定矩阵。所以我们不需要通过穷举所有的点来判断 v T H v v^THv vTHv是大于零还是小于零,而是直接利用 H H H是否正定来判断。而判断 H H H是否是正定矩阵可以通过求解 H H H的特征值来判断。如果所有的eigen value特征值都是正的,那么 H H H就是positive definite 正定矩阵。
所以判断条件就转化为:

如何逃离saddle point?
** H H H不只可以帮助我们判断,现在是不是在一个saddle point,还指出了参数可以update的方向。**注意这个时候 g = 0 g=0 g=0。
根据 λ x = A x \lambda x=Ax λx=Ax,可以对式子进行转化:

于是如果 λ < 0 λ<0 λ<0(eigen value<0),那 λ ‖ u ‖ 2 < 0 λ‖u‖2<0 λ‖u‖2<0,所以eigen value是负的,那这一整项就会是负的,也就是 u T H u u^THu uTHu是负的,也就是红色整项是负的,于是 L ( θ ) < L ( θ ′ ) L(\theta)<L(\theta') L(θ)<L(θ′)。也就是说令 θ ? θ ′ = μ \theta-\theta'=\mu θ?θ′=μ,在 θ ′ θ' θ′的位置加上 μ \mu μ,沿 μ \mu μ的方向做update得到 θ θ θ,就可以让loss变小。
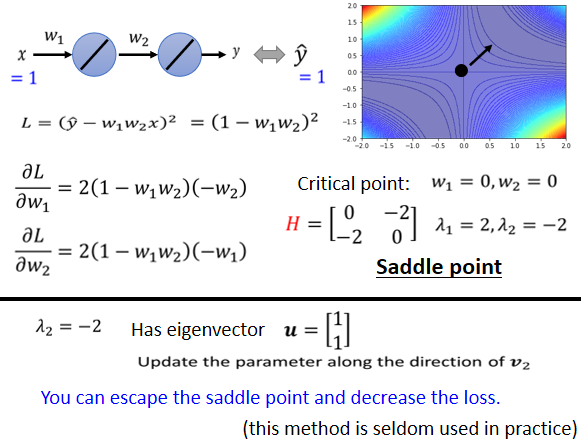
这个方法也有一点问题: H H H的运算量非常非常的大,还需要算其特征值和特征向量,运算量惊人,实际操作中还有其他方法可以逃离saddle point,在最糟糕的情况下还有这种方法可以逃离。
Saddle Point v.s. Local Minima
**事实上Local Minima没有那么常见。**一个可能的解释是:在低维的空间中,低维的一个参数的error surface,好像到处都是local minima,但是在高维空间来看,它可能只是一个saddle point。
如下图所示,几乎找不到完全所有eigen value都是正的critical point。下图这个例子种,minimum ratio代表正的eigen value的数目占总数的比例,最大也在0.5~0.6,代表只有一半的eigen value是正的,还有一半的eigen value是负的。
在这个图上,越往右代表critical point越像local minima,但是它们都没有真的,变成local minima。

batch/mini-batch和动量Momentum
batch/mini-batch
Optimization with Batch
每次在 Update 参数的时候,拿一个batch出来,算个 Loss,算个 Gradient,Update 参数,然后再拿另外个batch,再算个 Loss,算gradient,更新参数,以此类推。
mini-batch就是不把所有训练数据拿出来一起算loss,而是分小块。
所有的 Batch 训练过一遍,叫做一个 Epoch。
在生成batch的时候长春会做shuffle。
Shuffle 有很多不同的做法,常见的一个做法是在每一个 Epoch 开始之前,会分一次 Batch,每一个 Epoch 的 Batch 都不一样。
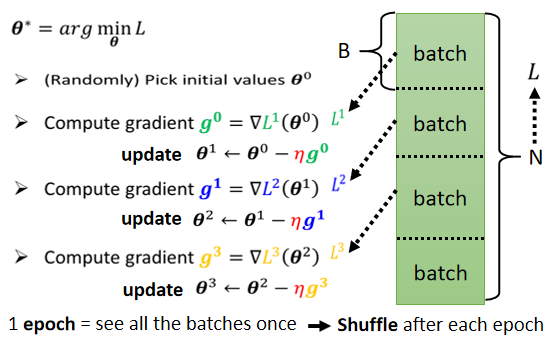
为什么要batch
直接上对比图:
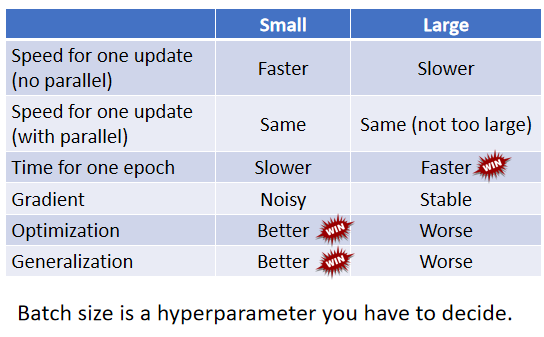
同一个model,batchsize过大效果反而更差?
用过大的batch size optimizer可能会有问题
小的batch在testing上表现更好-》overfitting
Momentum
Momentum是另外一个有可能可以对抗 Saddle Point,或 Local Minima 的技术。
传统的梯度下降
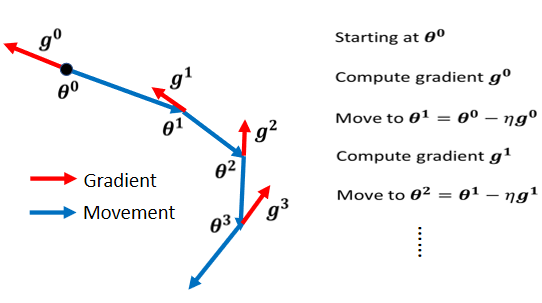
Gradient Descent + Momentum
加上 Momentum 以后,每一次在移动参数的时候,不是只往 Gradient 的反方向来移动参数,是 Gradient 的反方向+前一步移动的方向去调整去到参数
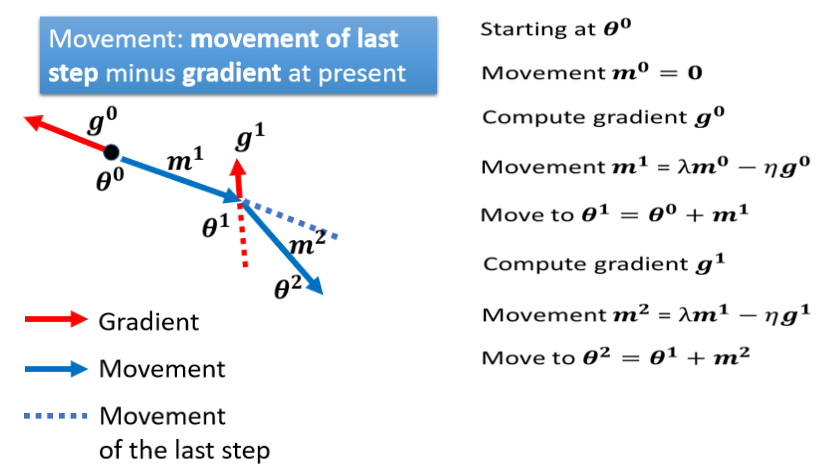
具体来看步骤如下:把蓝色的虚线加红色的虚线,前一步指示的方向跟 Gradient 指示的方向,当做参数下一步要移动的方向。
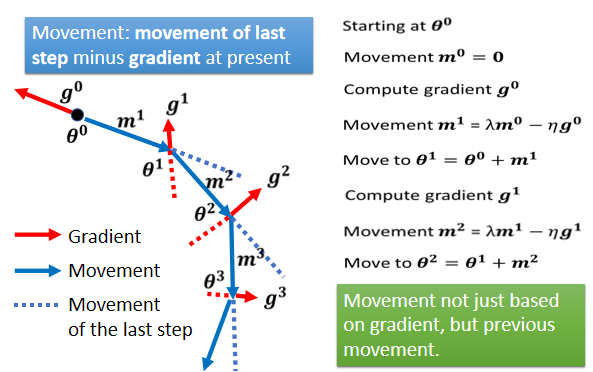

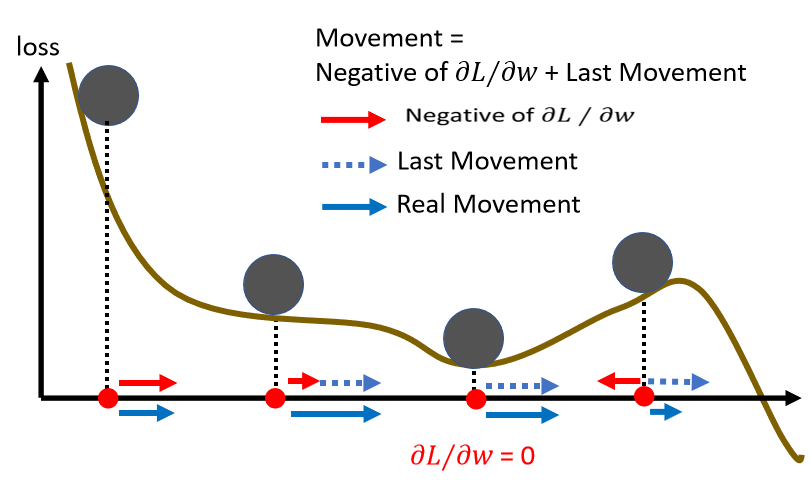
下面有一个例子来展示:
在第三步,Gradient 变得很小,但是没关系,如果有 Momentum 的话,根据上一步的Momentum 可以继续往前走;
甚至走到第四步时,Gradient 表示应该要往左走了,但是如果前一步的影响力,比 Gradient 要大的话,还是有可能继续往右走,甚至翻过一个小丘,可能可以走到更好 Local Minima。
自动调整学习率Adaptive Learning Rate(待更新)
critical point不一定是训练过程中最大的阻碍,思考一个问题:
loss不再下降的时候,gradient真的很小吗?
并不是的。如下图所示虽然loss不再下降,但是这个gradient的大小并没有真的变得很小。它可能在error surface山谷的两个谷壁间,不断的来回的震荡。
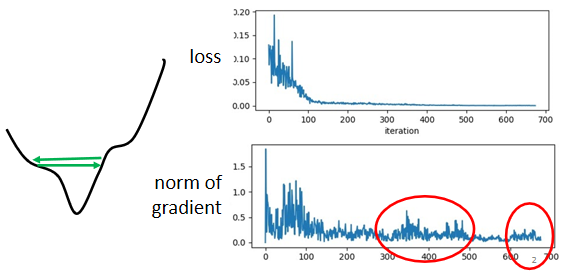
所以有的时候训练不下去的原因不是critical point,而是其他的原因。
举个例子:
在下面这个error surface中,纵轴的参数变化很小就会导致结果变化很大,而横轴参数变化很大结果变化很小。
如果两个参数使用同一个学习率,当学习率调的过大,在纵轴方向可能直接震荡:

如果学习率调的很小,在纵轴可以逐渐找到好的参数,但是在横轴更新时,由于学习率过小,更新速度太慢,也很难找到最优解。
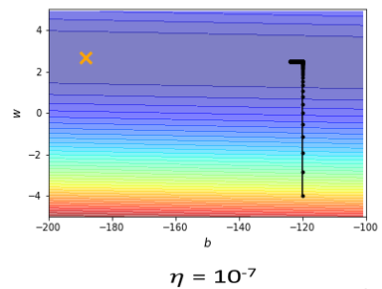
所以可以考虑为不同的参数和不同的iteration设置不同的learning rate。
为不同的参数和不同的iteration设置不同的learning rate
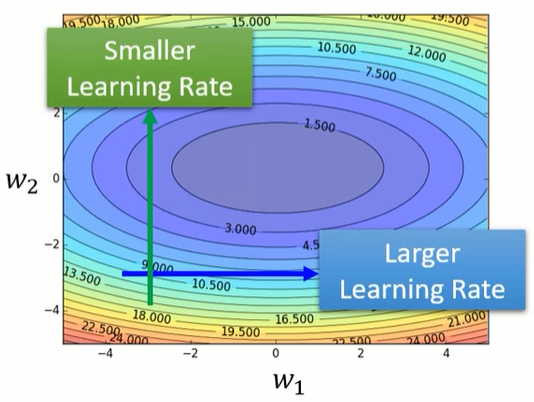
上面的案例展示了下面两个大原则:
- 如果在某一个方向上,gradient的值很小,非常的平坦,那我们会希望learning rate调大一点;
- 如果在某一个方向上非常的陡峭,坡度很大,那其实learning rate可以设得小一点;
Root mean square
常见的计算σ可以用gradient的Root Mean Square。

现在参数要update的式子,从θ??初始化参数减掉g??,乘上learning rate η除以σ??,就得到θ?1,
同一个参数同一个方向也希望可以自适应调整
learning rate scheduling
warm up
损失函数(待更新)
为什么crossentropy更常用在分类上
MSE在loss很大的地方gradient很小,如果初始就在loss很大的地方,gradient又很小,很难训练
batch normalization(待更新)
能不能修改error surface,让模型更好训练?
feature normalization
internal covariate shift