Week1 入门代价函数线性回归梯度下降

基于吴恩达《机器学习》课程
本篇博客为第一周的内容。

1 引言

监督学习：回归问题（连续输出）、分类问题（离散结果）

无监督学习：聚类算法、鸡尾酒宴问题

2 单变量线性回归

回归：根据之前的数据预测出一个准确的输出值

2.1 变量表示

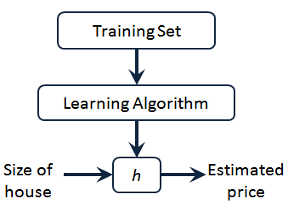
在这里插入图片描述
m代表训练集中实例的数量

x代表特征/输入变量

y代表目标变量/输出变量

(x,y)代表训练集中的实例

$x^{(i)},y^{(i)})$ 代表第 $i$ 个观察实例

h代表学习算法的解决方案或函数也称为假设函数（hypothesis）

$\theta_{0} \theta_{1}…$ 为参数（parameters）

建立的模型（假设函数）只含有一个特征/输入变量，这样的问题叫作单变量线性回归问题：

$h_\theta \left( x \right)=\theta_{0} + \theta_{1}x$

2.2 代价函数

模型所预测的值与训练集中实际值之间的差距 $h_{\theta}(x^{(i)})-y^{(i)}$ 就是建模误差 （modeling error ）。

我们的目标便是选出可使得建模误差的平方和 最小的参数（parameters ） $\theta_{0}$ 和 $\theta_{1}$ ，即使得代价函数 （平房误差函数）最小：

$\left( \theta_0, \theta_1 \right) = \frac{1}{2m}\sum\limits_{i=1}^m \left( h_{\theta}(x^{(i)})-y^{(i)} \right)^{2}$

$\frac{1}{2}$ 是为了后续求导方便， $\frac{1}{m}$ 仅是使结果较小。

2.3 梯度下降

用于求代价函数 $J(\theta_{0}, \theta_{1})$ 的最小值，得到最小值对应的参数 $\theta_{0}$ 和 $\theta_{1}$ 。

开始时随机选择一个参数组合，持续寻找下一个能让代价函数值下降最多的参数组合，直到找到一个局部最小值（local minimum ），选择不同的初始参数组合，可能会找到不同的局部最小值。

批量梯度下降（batch gradient descent ）算法的公式为：
在这里插入图片描述
$: =$ 表示赋值（assignment ）

$\alpha$ 是学习率（learning rate ）或步长

梯度下降中，当 $j = 0$ 和 $j = 1$ 时，会产生更新。每次要同时更新 ${\theta_{0}}$ 和 ${\theta_{1}}$ ，而不能先更新 ${\theta_{0}}$ 用更新后的值更新 ${\theta_{1}}$ 。
[(img-btFIXirk-1632408179403)(image/image_1.png)]
如果 $\alpha$ 太小会步数太多太慢，太大可能会导致无法收敛，甚至发散。

当接近局部最低时，导数值会自动变得越来越小，所以梯度下降将自动采取较小的幅度，所以实际上没有必要再另外减小 $\alpha$ 。

2.4 梯度下降的线性回归

线性回归模型：

$h_\theta \left( x \right)=\theta_{0} + \theta_{1}x$

$\left( \theta_0, \theta_1 \right) = \frac{1}{2m}\sum\limits_{i=1}^m \left( h_{\theta}(x^{(i)})-y^{(i)} \right)^{2}$

梯度下降算法：
在这里插入图片描述
用梯度下降求解线性回归，关键在于求代价函数的偏导：

$\frac{\partial }{\partial {{\theta }_{j}}}J({{\theta }_{0}},{{\theta }_{1}})=\frac{\partial }{\partial {{\theta }_{j}}}\frac{1}{2m}{{\sum\limits_{i=1}^{m}{\left( {{h}_{\theta }}({{x}^{(i)}})-{{y}^{(i)}} \right)}}^{2}}$

将 $h_\theta \left( x \right)=\theta_{0} + \theta_{1}x$ 代入后求偏导（此时 $\frac{1}{2}$ 就起作用了）：

$j = 0$ 时： $\frac{\partial }{\partial {{\theta }_{0}}}J({{\theta }_{0}},{{\theta }_{1}})=\frac{1}{m}{{\sum\limits_{i=1}^{m}{\left( {{h}_{\theta }}({{x}^{(i)}})-{{y}^{(i)}} \right)}}}$

$j = 1$ 时： $\frac{\partial }{\partial {{\theta }_{1}}}J({{\theta }_{0}},{{\theta }_{1}})=\frac{1}{m}\sum\limits_{i=1}^{m}{\left( \left( {{h}_{\theta }}({{x}^{(i)}})-{{y}^{(i)}} \right)\cdot {{x}^{(i)}} \right)}$

则梯度下降算法可改写成：

Repeat {

???? ${\theta_{0}}:={\theta_{0}}-a\frac{1}{m}\sum\limits_{i=1}^{m}{ \left({{h}_{\theta }}({{x}^{(i)}})-{{y}^{(i)}} \right)}$

???? ${\theta_{1}}:={\theta_{1}}-a\frac{1}{m}\sum\limits_{i=1}^{m}{\left( \left({{h}_{\theta }}({{x}^{(i)}})-{{y}^{(i)}} \right)\cdot {{x}^{(i)}} \right)}$