机器学习可以理解为是让机器自动寻找函数的一个过程。

根据函数功能的不同,可以将机器学习进行以下分类。
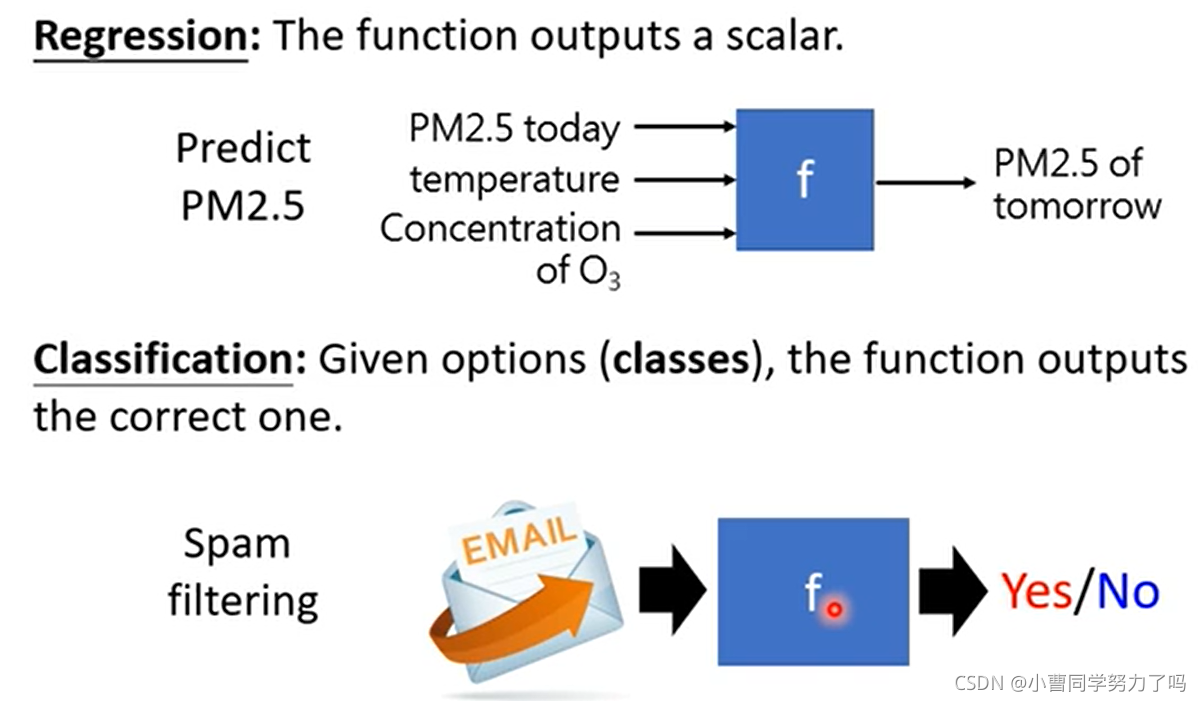
Alpha Go做的事情也是一个分类问题:将当前棋盘上白子黑子的位置作为输入,输出是19*19个calsses中的一个。
如果知道了李宏毅老师Youtube过去三年每一天的播放量数据,去预测明天的播放量数据,可以假定一个包含了两个参数w和b的线性模型,输入x1为前一天的数据(如2.25),y为预测的当前一天的数据(如2.26)


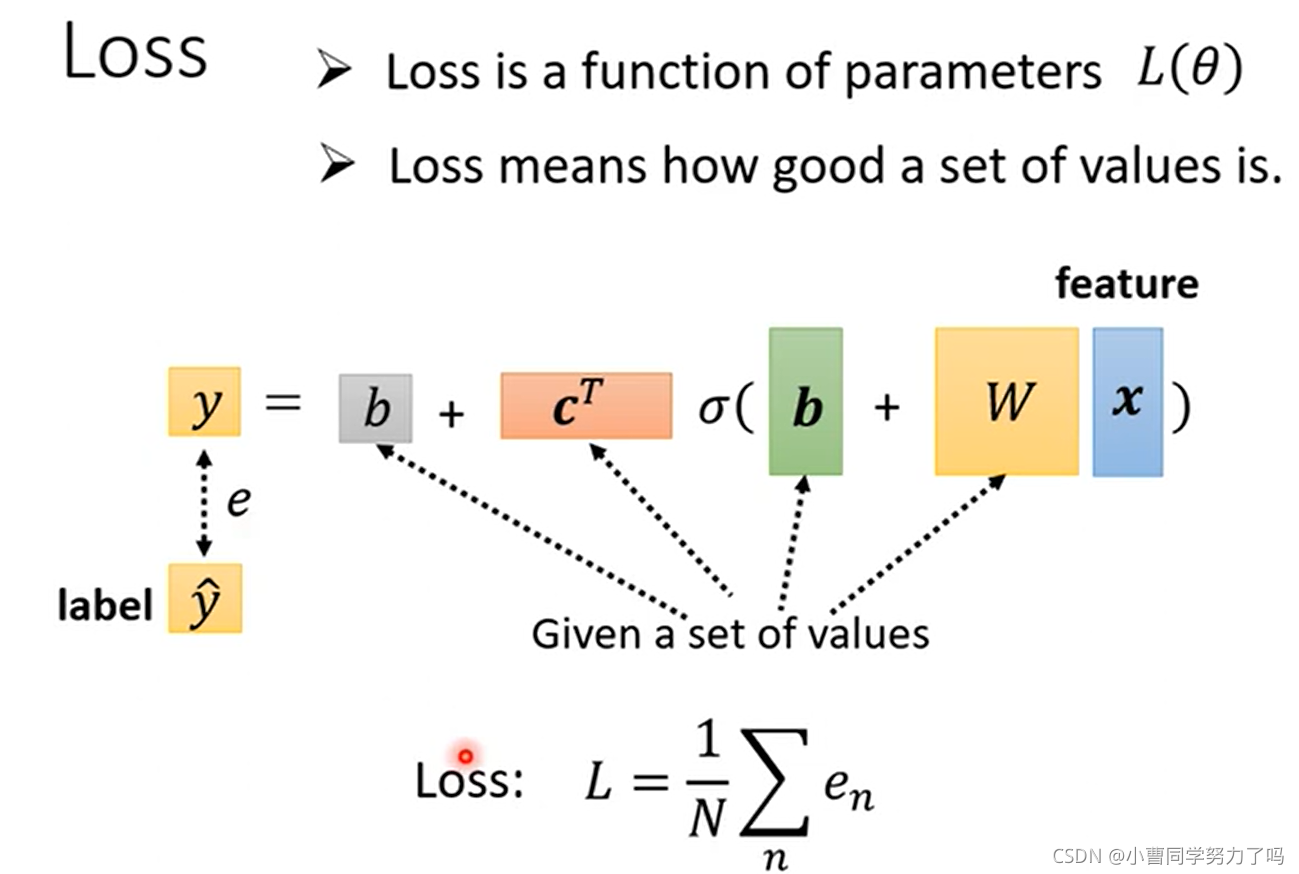
损失函数是一个关于模型参数的函数,用来评价模型及模型参数选择的优劣,此处我们可以通过平均绝对误差进行评价。将第一天的数据代入模型函数得到第二天的预测值,与真实值相差的绝对值为e1,类似的将第二天数据代入预测第三天,与第三天真实值之差的绝对值为e2,最后得到en,并把这些相加取平均,这就是平均绝对误差(MAE)。除此之外,还有MSE(均方误差)以及RMSE(均方根误差)等。


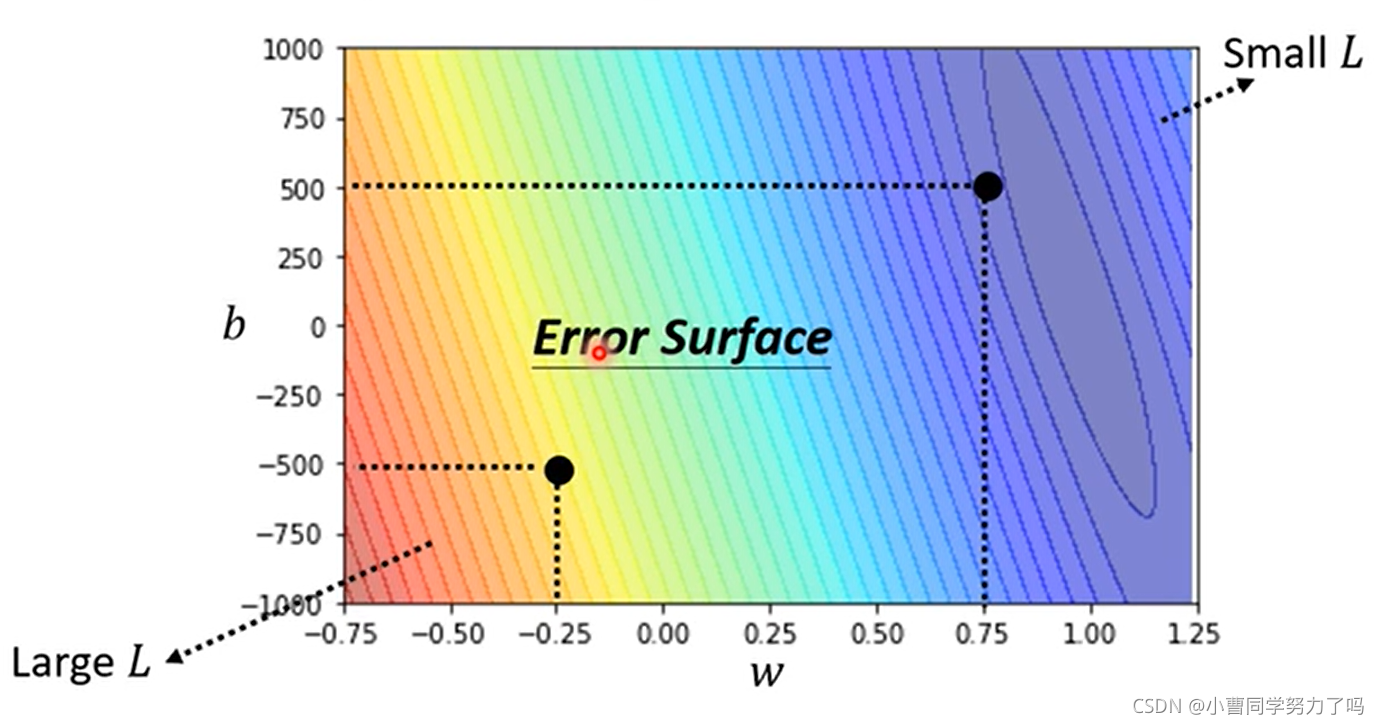
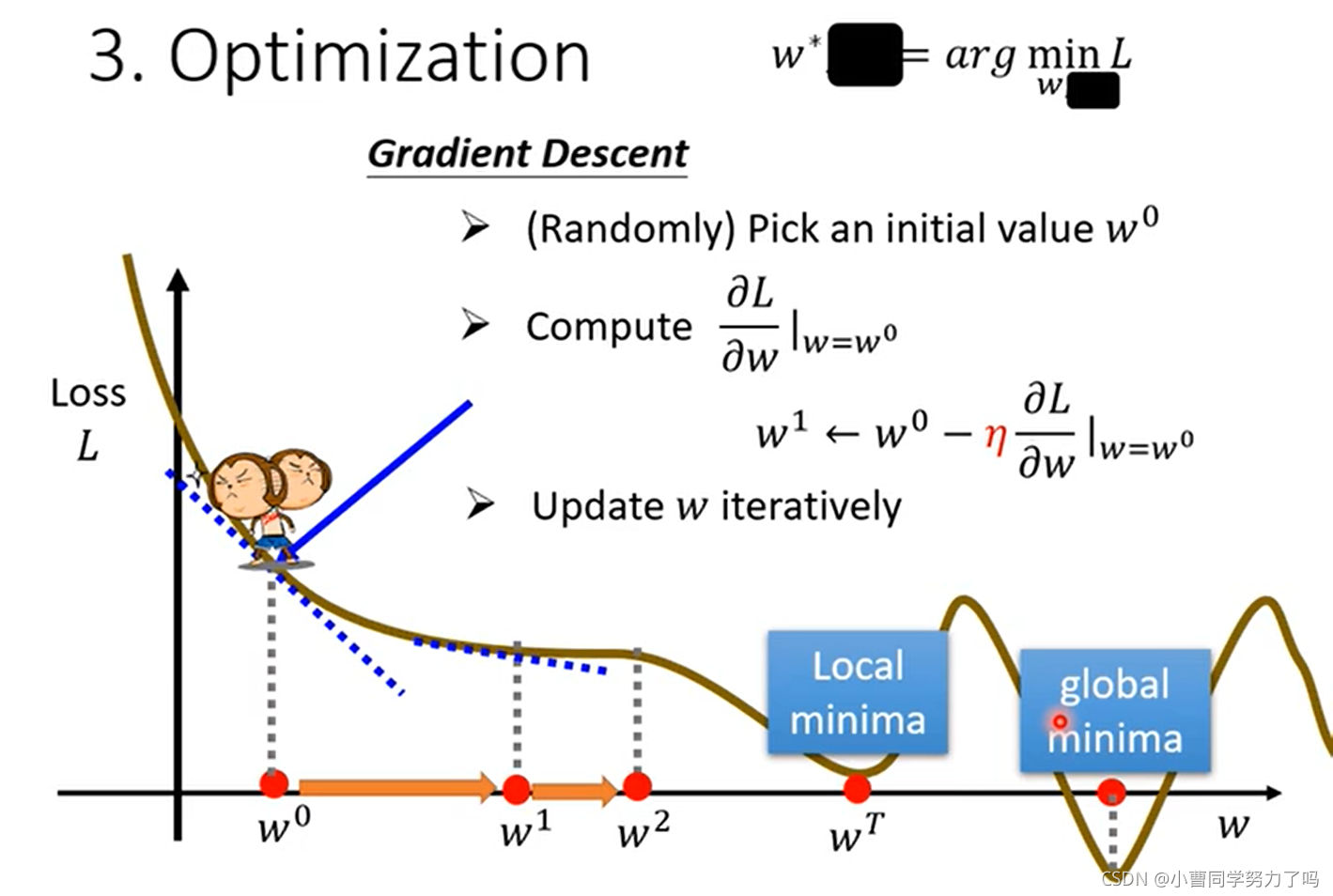
我们可以尝试不同的参数w和b,都去计算loss的值,并绘制出等高线图,其中越偏红色系表示loss越大,越偏蓝色系表示loss越小,最好的参数应该在w=1,b=250附近。更精确的寻找的话,可以通过梯度下降的方法。如下图中我们就是将b确定,L关于w参数变化的误差曲线,梯度下降每次前进的距离既与当前点导数相关,也与我们自己设置的参数学习率有关,像这样w和b由机器自己学习得到的参数就是模型的参数,我们可以设置的学习率等参数就称为超参数(hyperparameters),当权值迭代到wt时,此时梯度变为0,权值就不会再更新,容易看出,梯度下降是容易陷入局部最小的,但是在实际的应用中,反而往往不会陷入局部最小,这也不是我们在做例如神经网络的训练时所关注的问题。
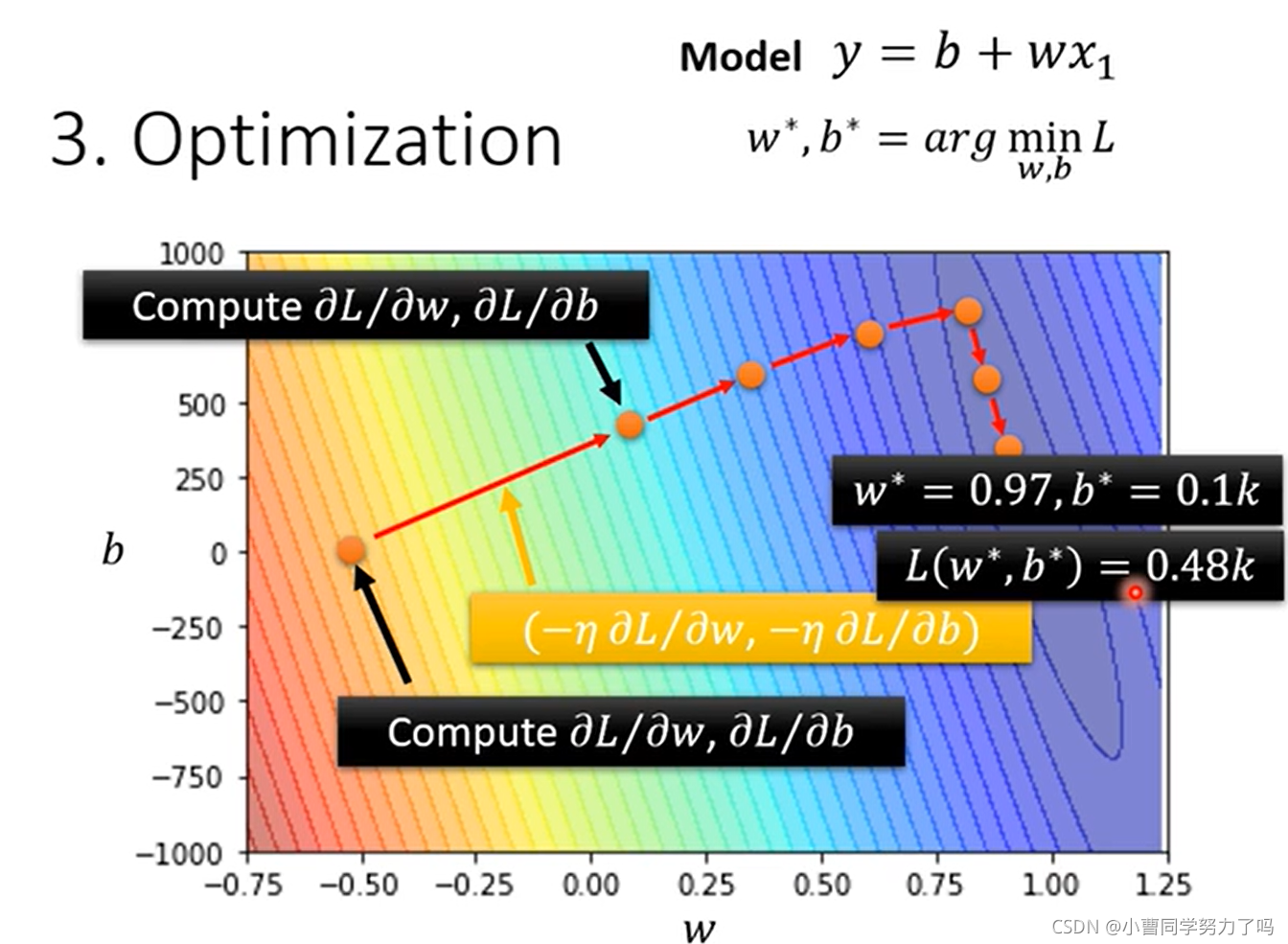
学习的参数有两个时也是类似的做法,如下:

梯度为负时,需要朝着梯度为0的方向增大,梯度为正时,则需要向着梯度为0的方向减小,所以会带有负号。
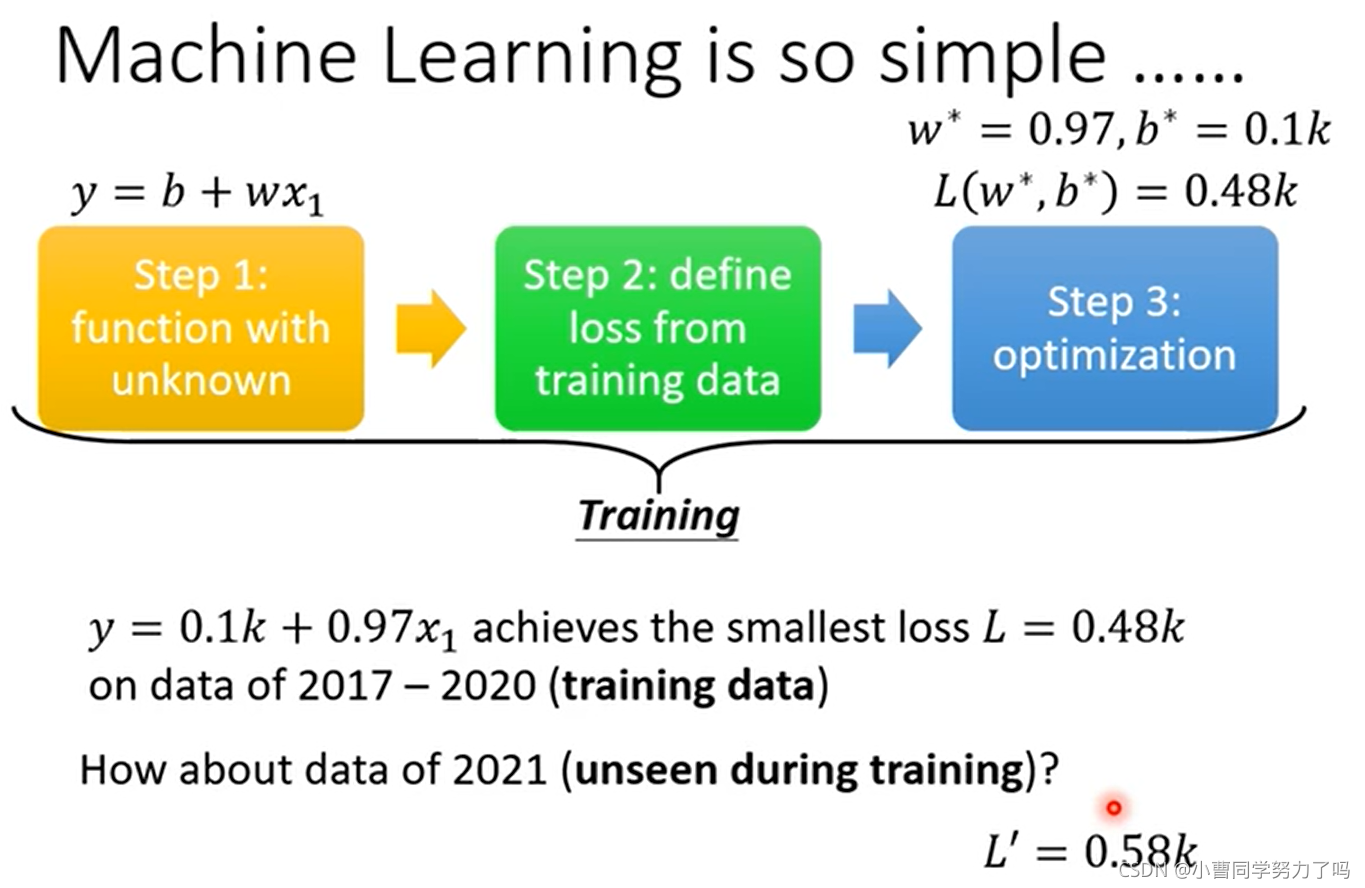
这时我们就完成了模型的训练,此处我们选择线性model在训练集上实现的最低的loss是0.48k,之后预测未来2021.1.1到2021.2.14的数据,得到的与真实值的差的绝对值的平均值为0.58k.

上图给出了1.1到2.14预测值与真实值的比较,可以看出除了第一天之外,其余每一天的数据都像是把前一天的数据直接向右平移,这是不难理解的,因为每一天预测值的点都是前一天的真实值乘以0.97再加上100,所以差别不会很大。但是我们这个时候会发现其实真实值呈现的是由一定的周期性的:一般以7为一个周期,具体解释可能就是周末两天大家会出去玩,那么我们在发现这个规律之后,还用前一天去预测下一天就不太合适了,而应该去用前七天的数据预测下一天的。

在第二行中,列出了此时的model,wj表示的是j天前,从最后训练得到的权值来看,前一天的权重对应为0.79,对下一天的预测的影响是最大的,最后得到的训练集和测试集上的loss分别是0.38k和0.49k,之后我们再尝试使用前更多天的数据,两个loss就不会降太多了。此时我们使用的都是liner model,可见这种简单的model的性能到这里可能就不会提升了。
紧接着我们引入了分段线性函数,如下面的红色曲线,他可以由若干个蓝色曲线进行叠加再加上常量得到,对于一个一般的曲线,我们可以用很多个点将他分开,再依次用直线将这些点连接起来,这样我们就得到了一个比较复杂的分段线性函数,这一函数也可以通过下面的方式进行叠加,只不过可能蓝色的曲线会用到很多。
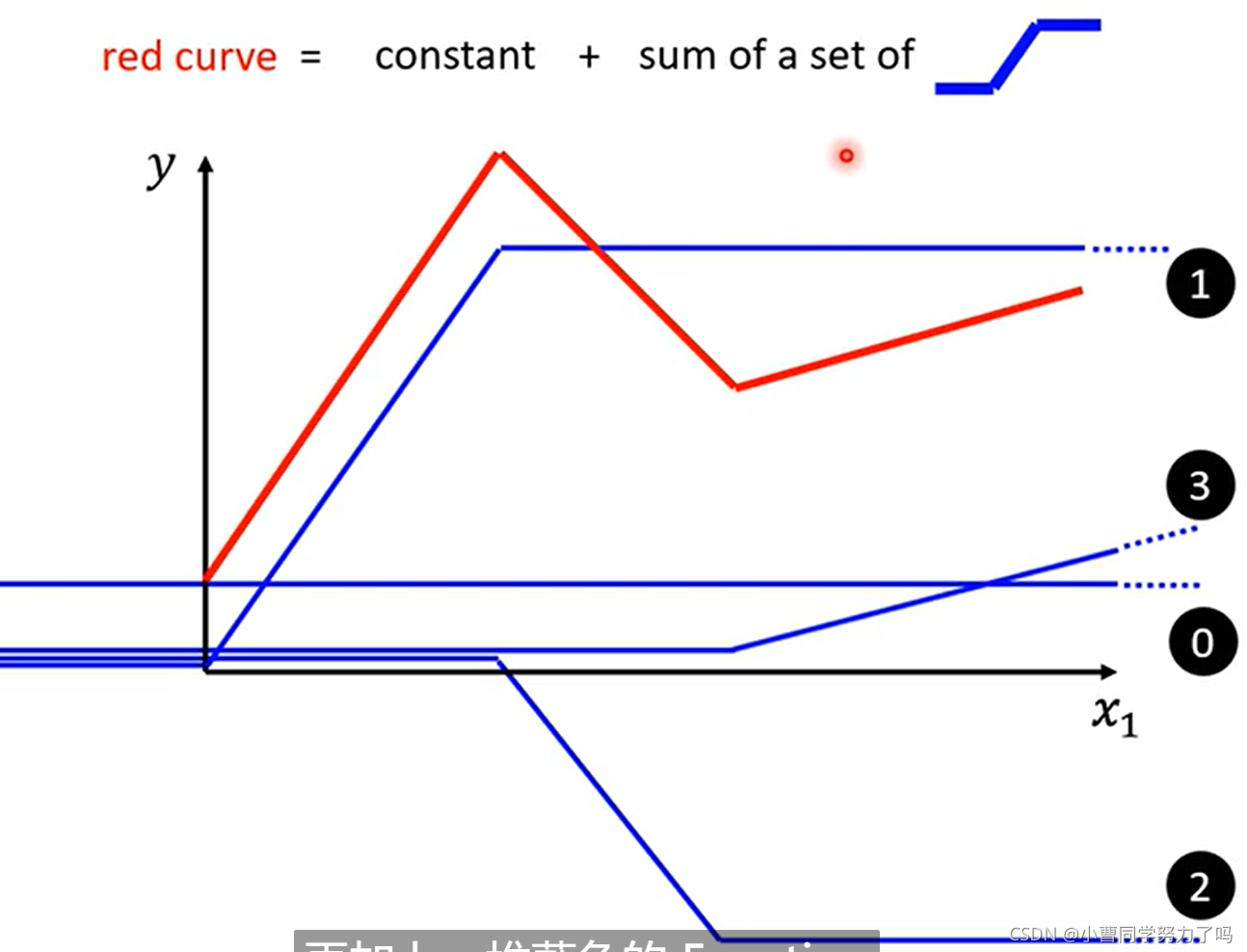
在明白任意的曲线都可以通过这种方式进行逼近后,我们需要知道蓝色曲线的函数是怎么样的,如下它就是由sigmoid函数变化而来,而由于转向比较犀利,被称为Hard Sigmoid。

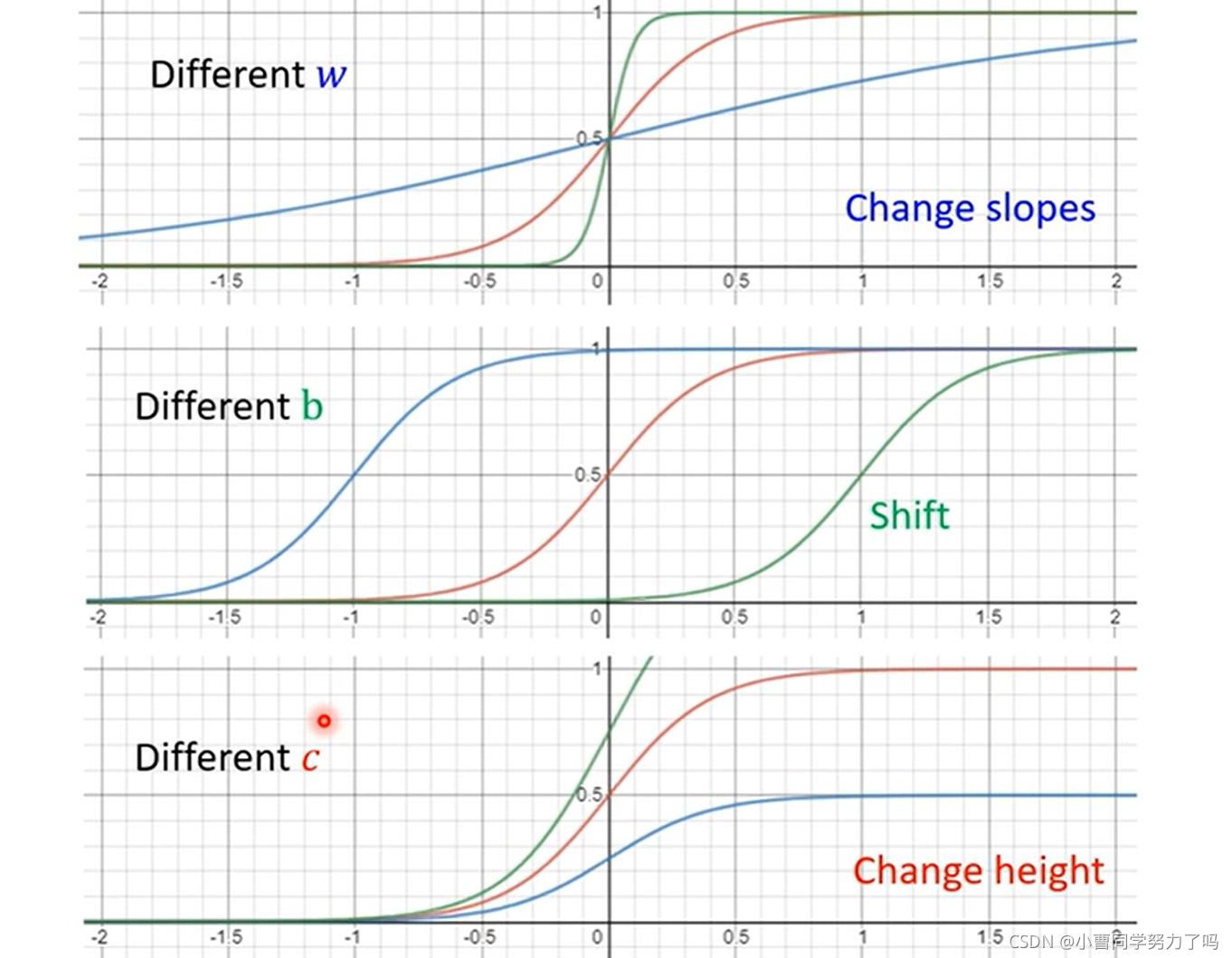
其中的参数w、b、c对sigmoid图像的影响如下:

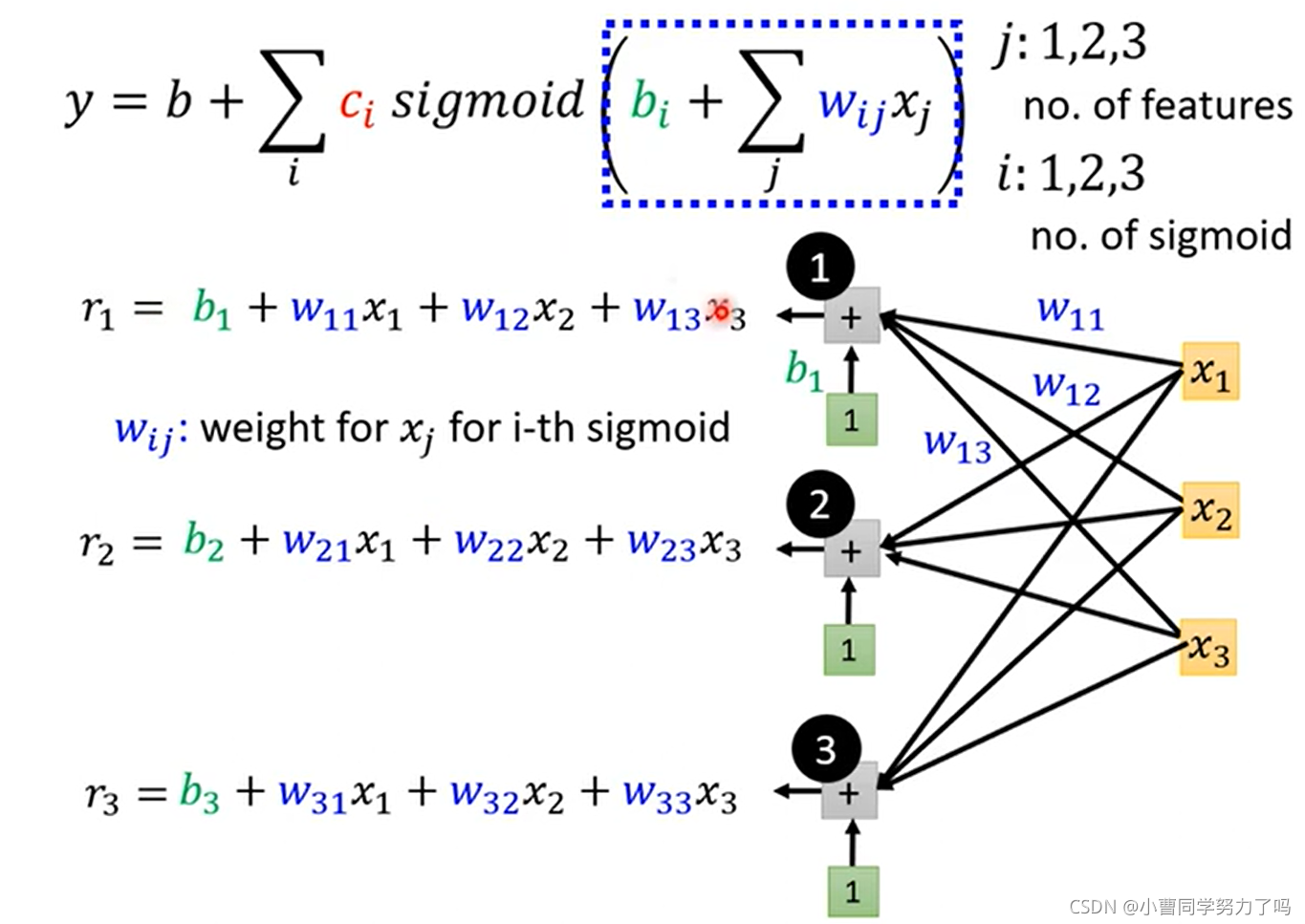
如上,我们将线性模型扩展成通过若干个sigmoid函数叠加外加常数项逼近的任意的曲线,将考虑前j天的线性模型扩展成最终的考虑多天的任意曲线的模型。
上图做的事情是:模型采用下图中的红色分段线性函数,然后特征选择前三天的播放量,以此来预测下一天的播放量。这样我们就绘制出了上图中的网络的拓扑结构。

之后我们把x到r表示成矩阵乘法的关系。

最终的网络结构如下:
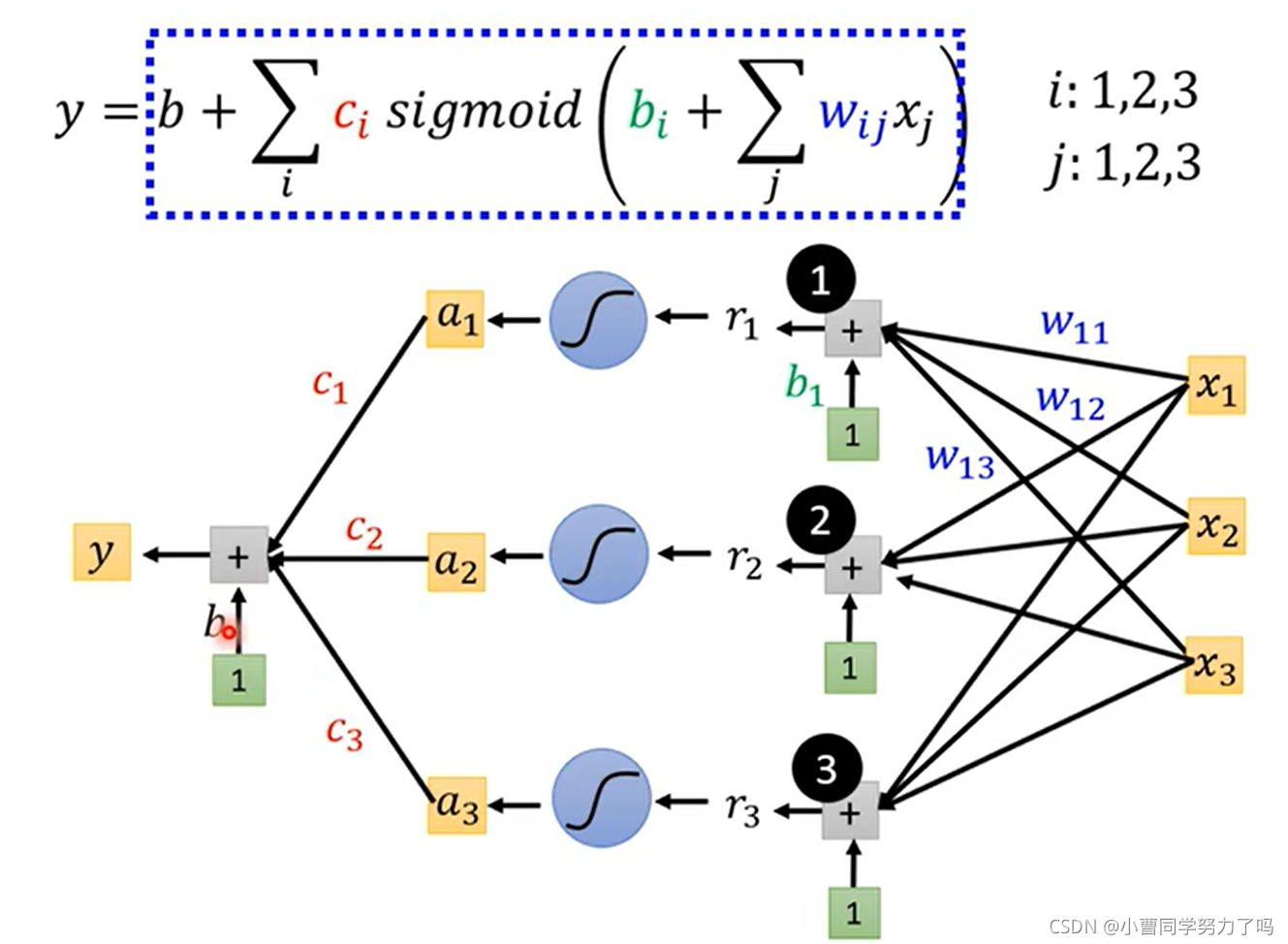
表示成线性代数中向量矩阵相乘的形式即为下图下方的式子。
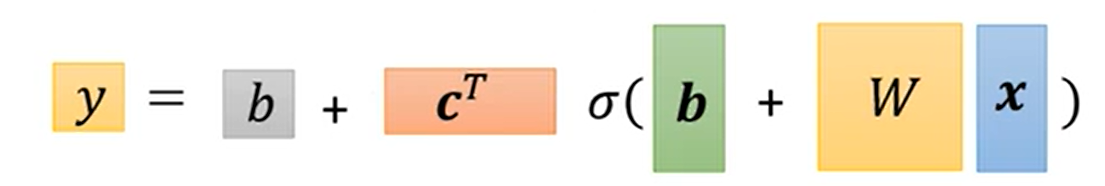
在得到这样一个稍微复杂些的model之后,我们发现其中需要确定的参数很多,包括了标量b、向量c的转置、向量b、矩阵W,我们将所有元素都放在一个一维的行向量或列向量中,每个元素以seita标注,以方便后续利用梯度下降求解最优参数,下图一即为定义此模型下的loss函数,下图二和三即为通过梯度下降寻找参数最优解的一个过程,迭代到梯度为0或者次数过多我们不想做为止。

通常由于数据集比较大,我们会将数据集分成若干个batch,分批去进行参数寻优,每一个batch中的一次参数寻优称作一次update或者iteration,所有的batch都进行完一次之后,称作一个epoch。例如:一个数据集包含了1000个样本,我们把它分成100组,每一组中有10个样本,那么每一组中每一次的参数迭代就称作一次update,所有的batch都完成这一次参数迭代后就称作一个epoch,所以此时一个epoch实际包含了1000次update。
到此为止,我们可以处理的超参数包括了学习率、sigmoid函数的个数(即神经元节点数)、组的个数(batch size),这些都是我们可以自己调节的参数。
在上面进行曲线拟合的过程中,我们除了使用sigmoid函数外,还可以使用ReLU函数(Rectified Linear Unit,整流线性单元函数)进行函数曲线的拟合。
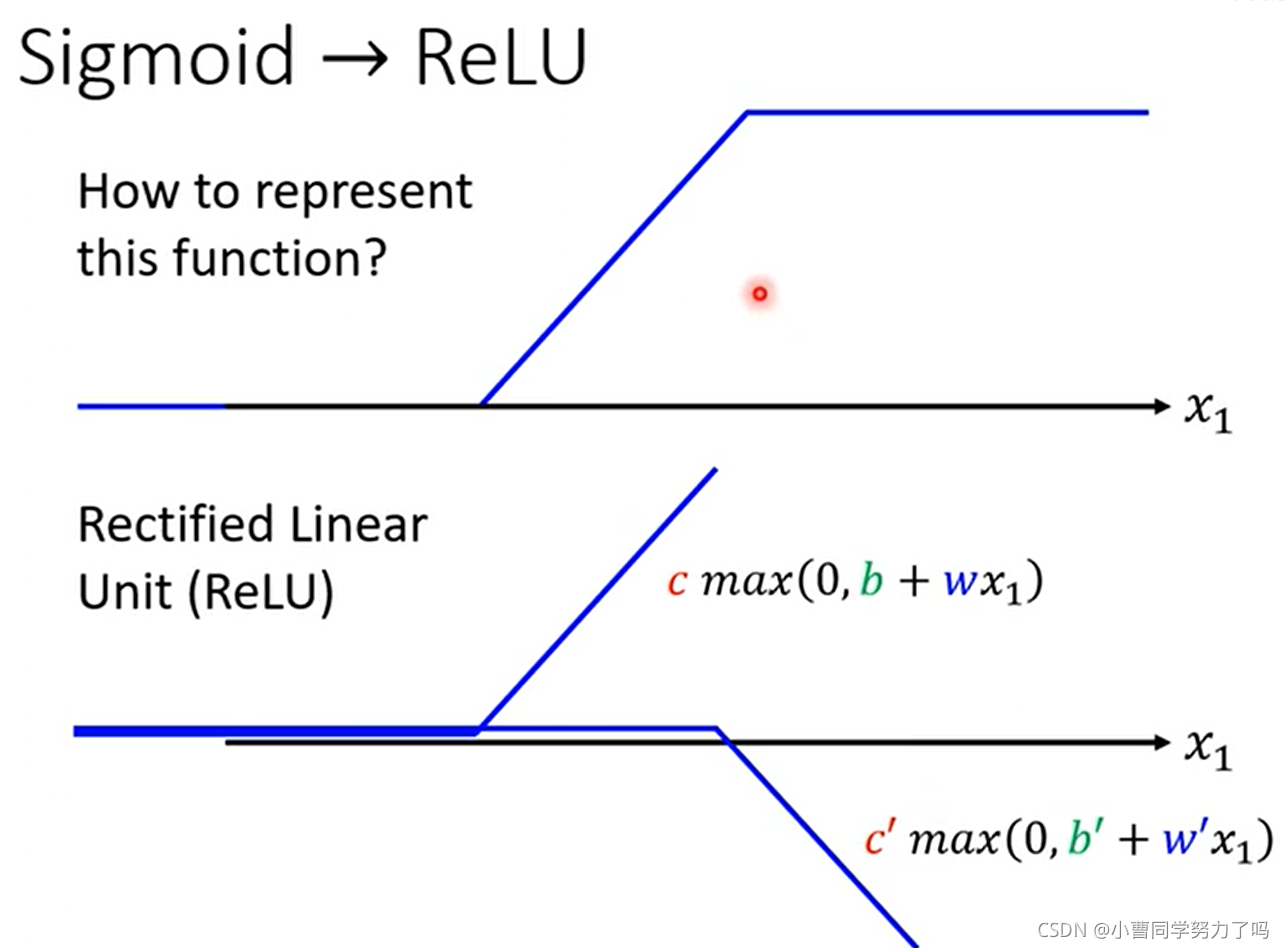

上图中要注意的地方是ReLU函数的累加符号下边是2i,这是因为两个ReLU函数才可以叠加成一个hard sigmoid函数,而后者是使用sigmoid进行函数拟合的基本单元。
这就是两种最常见的激活函数,我们通过这些激活函数输出的叠加来拟合模型中的函数曲线。
使用ReLU函数作为激活函数后,通过选择不同的神经元个数,得到的训练集和测试集上损失函数的值如下:

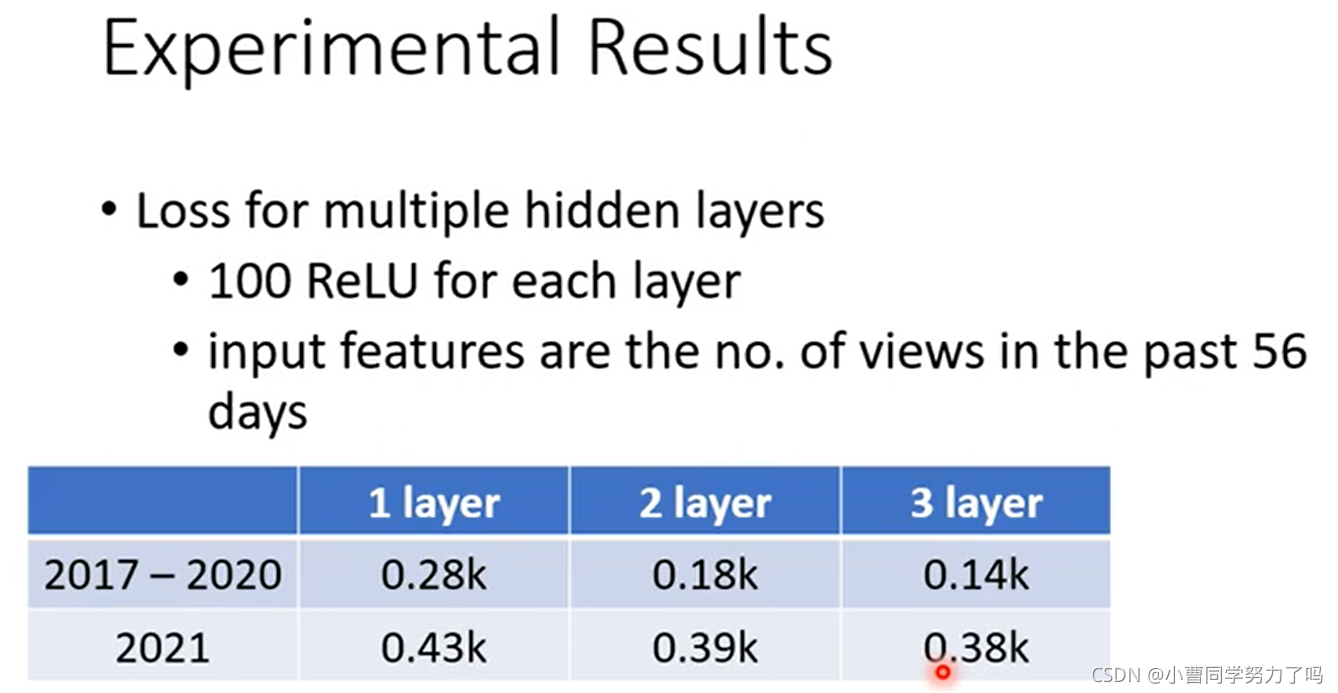
进一步,我们可以通过增加神经网络的层数来实现更低的Loss。

结果如下,其中每一层都包含了100个激活函数为ReLU的神经元,输入的特征是前56天的播放量数据(在线性模型中,采用56时得到了尽可能低的loss)。
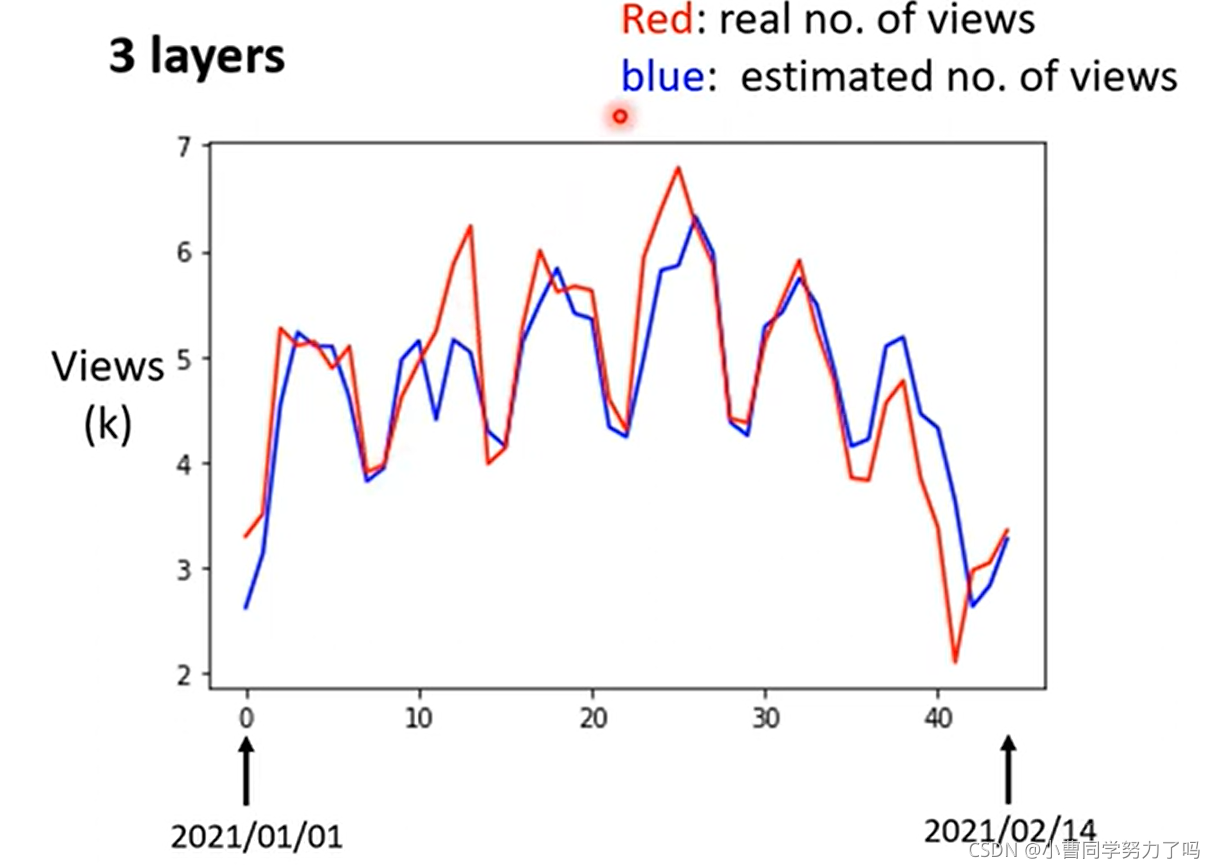
测试集中真实值与预测值的对比如下。

当再增加层数时,虽然在测试集上表现更加优异了,但是训练集上结果反而变差,这就出现了过拟合,网络此时就陷入了自我小世界。