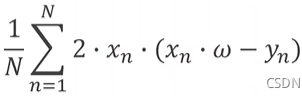[人工智能]（深度学习第二课）如何理解梯度下降算法？

教程

在上一节课中，我们通过穷举找出了最适合的 w ，使得 y =x*w 最接近于样本。

但在一个神经网络中，有成百上千万的节点，穷举给每一个节点找最适合的 w 往往是不可能的。

因此，我们的目标就是给每一个节点找到最适合的 w ，就成为了一个优化问题。

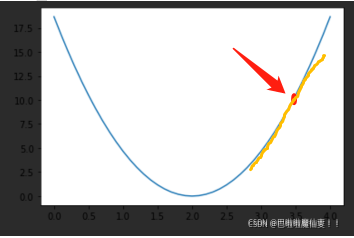
首先，我们给 w 一个随机的初始值，在图中的红点处

此时，w 的坐标为 （w，loss(w)） ，对其求导，可得黄色直线的 斜率k ，根据 k的正负 ，就可以知道w往哪边优化可以使 w减小

下图是在cost（上文中的loss）中对w求导。

又知w的更新公式为：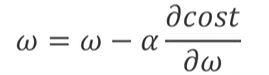

α 为学习率

根据上述公式，经过多轮的迭代（即多个epoch），w总会到达一个局部最优值（或全局最优值）

实现代码

x_data = [1.0,2.0,3.0]
y_data = [2.0,4.0,6.0]

def forward(x):
    return x * w

w = 1.0
def cost(xs,ys):
	# 计算损失
    cost = 0
    for x,y in zip(xs,ys):
        y_pred = forward(x)
        cost += (y_pred - y) ** 2
    return cost/len(xs)

def gradient(xs,ys):
	# 计算梯度
    grad = 0
    for x,y in zip(xs,ys):
        grad += 2*x*(x*w -y)
    return grad / len(xs)

for epoch in range(100):
    cost_val = cost(x_data,y_data)
    grad_val = gradient(x_data,y_data)
    w -= 0.01 * grad_val
    print(f"Epochs:{epoch},w={w},loss={cost_val}")
print(f"predict y:{forward(4)}")

如何避免w陷入局部最优值？

这里的w每次都是用 全部的 x 计算得出的y_pred 去计算 loss，这种方法称为：批量梯度下降
优点：梯度更稳定，收敛稳定。可以并行
缺点：需要计算全部的数据后，才更新一次w，速度慢

于是有人提出了 随机梯度下降 ，即随机使用之前得出的loss 去更新这一次的w，每得出一个loss，都更新一次w，更新速度非常快。计算公式为：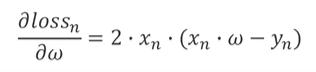

这里与上面批量梯度下降的区分开。上面的是

优点：梯度可能下降快。可以避免局部最小值。
缺点：只能串行。且收敛不稳定。

还有一种折中的方式，小批量梯度下降 。即不计算全部的数据再更新w，也不会每次都更新w。上述两种方法的折中。

这里的“批量”就是 batch