Gradient Descent
Network parameters θ = { w 1 , w 2 , ? ? , b 1 , b 2 , ? ? } \theta=\left\{w_{1}, w_{2}, \cdots, b_{1}, b_{2}, \cdots\right\} θ={w1?,w2?,?,b1?,b2?,?}
Starting Parameters θ 0 ? θ 1 ? θ 2 ? … … \theta^{0} \longrightarrow \theta^{1} \longrightarrow \quad \theta^{2} \longrightarrow…… θ0?θ1?θ2?……
C o m p u t e ? ? L ( θ 0 ) θ 1 = θ 0 ? η ? L ( θ 0 ) C o m p u t e ~ \nabla \mathrm{L}\left(\theta^{0}\right) \quad \theta^{1}=\theta^{0}-\eta \nabla \mathrm{L}\left(\theta^{0}\right) Compute??L(θ0)θ1=θ0?η?L(θ0)
C o m p u t e ? ? L ( θ 1 ) θ 2 = θ 1 ? η ? L ( θ 1 ) C o m p u t e ~ \nabla \mathrm{L}\left(\theta^{1}\right) \quad \theta^{2}=\theta^{1}-\eta \nabla \mathrm{L}\left(\theta^{1}\right) Compute??L(θ1)θ2=θ1?η?L(θ1)
Millions of parameters ……
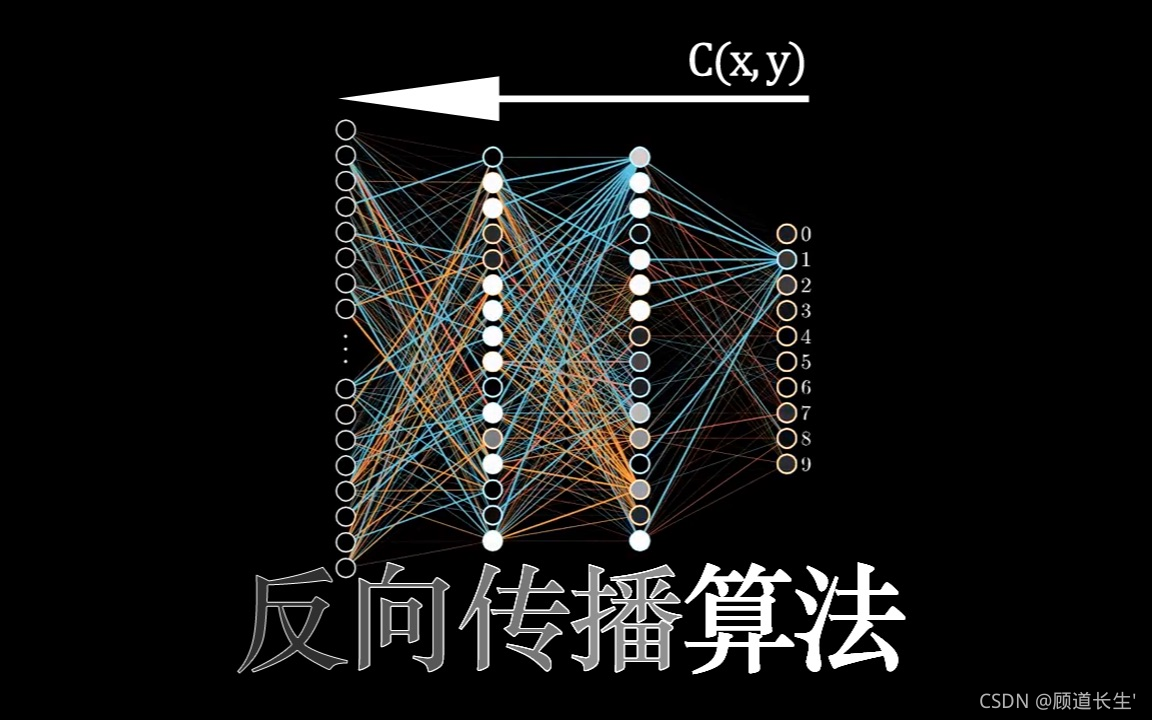
To compute the gradients efficiently,
we use backpropagation.
Chain Rule
Case1
y = g ( x ) z = h ( y ) y=g(x) \quad z=h(y) y=g(x)z=h(y)
Δ x → Δ y → Δ z \Delta x \rightarrow \Delta y \rightarrow \Delta z \quad Δx→Δy→Δz
d z d x = d z d y d y d x \frac{d z}{d x}=\frac{d z}{d y} \frac{d y}{d x} dxdz?=dydz?dxdy?
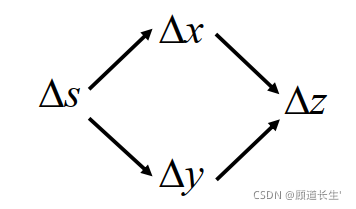
Case 2
x = g ( s ) y = h ( s ) z = k ( x , y ) x=g(s) \quad y=h(s) \quad z=k(x, y) x=g(s)y=h(s)z=k(x,y)
d
z
d
s
=
?
z
?
x
d
x
d
s
+
?
z
?
y
d
y
d
s
\frac{d z}{d s}=\frac{\partial z}{\partial x} \frac{d x}{d s}+\frac{\partial z}{\partial y} \frac{d y}{d s}
dsdz?=?x?z?dsdx?+?y?z?dsdy?
Backpropagation
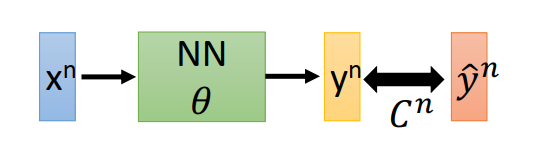
L ( θ ) = ∑ n = 1 N C n ( θ ) ? ? > ? L ( θ ) ? w = ∑ n = 1 N ? C n ( θ ) ? w L(\theta)=\sum_{n=1}^{N} C^{n}(\theta) --> \frac{\partial L(\theta)}{\partial w}=\sum_{n=1}^{N} \frac{\partial C^{n}(\theta)}{\partial w} L(θ)=n=1∑N?Cn(θ)??>?w?L(θ)?=n=1∑N??w?Cn(θ)?
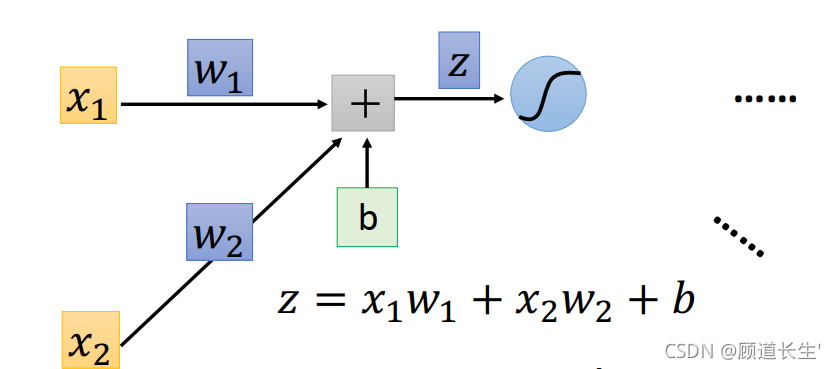
计算 ? C ? w \frac{\partial C}{\partial w} ?w?C?,可以计算 ? z ? w ? C ? z \frac{\partial z}{\partial w} \frac{\partial C}{\partial z} ?w?z??z?C?
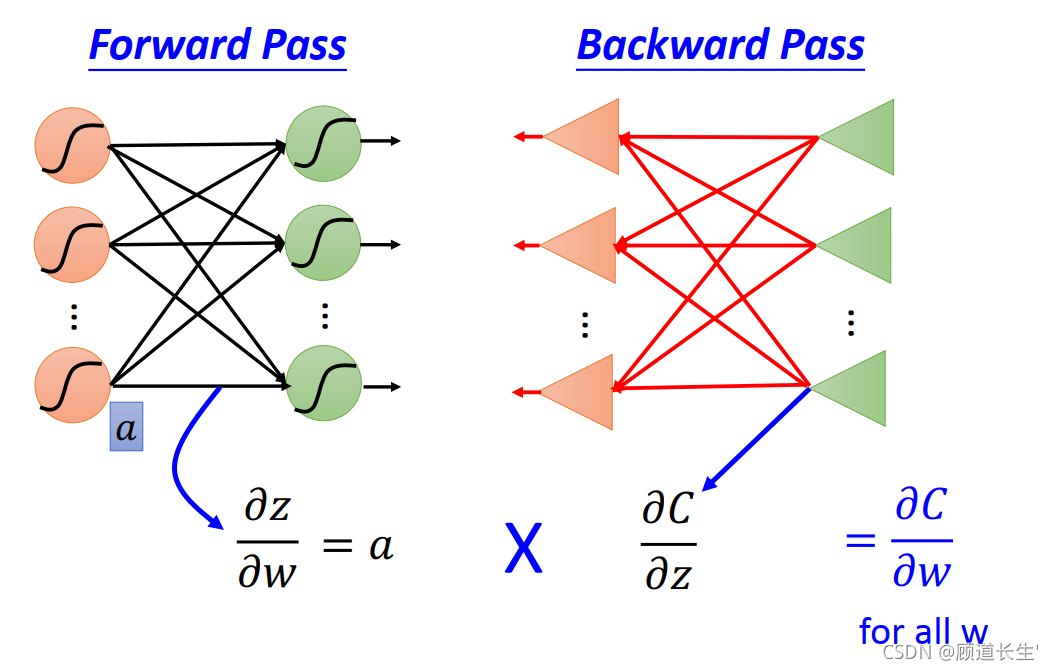
Forward pass:
Compute 𝜕𝑧/𝜕𝑤 for all parametersBackward pass:
Compute 𝜕𝐶/𝜕𝑧 for all activation
function inputs z
Forward pass
先考虑 ? z ? w \frac{\partial z}{\partial w} ?w?z? 这一项, 完全可以秒算出来, ? z ? w 1 = x 1 , ? z ? w 2 = x 2 \frac{\partial z}{\partial w_{1}}=x_{1}, \frac{\partial z}{\partial w_{2}}=x_{2} ?w1??z?=x1?,?w2??z?=x2?
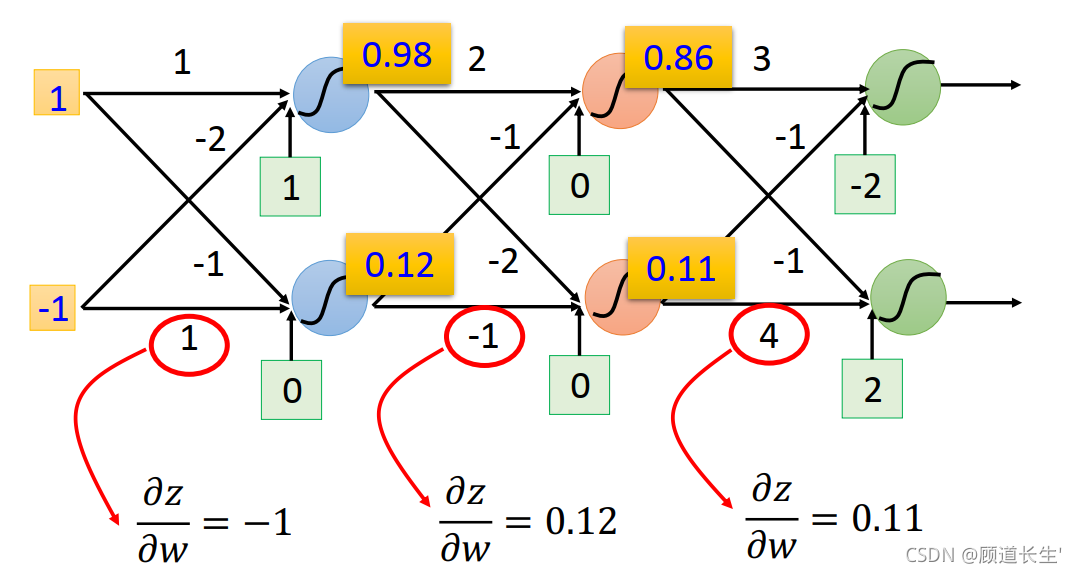
规律:求 ? z ? w \frac{\partial z}{\partial w} ?w?z? ,就是看w前面连接的input是什么,那微分后的 ? z ? w \frac{\partial z}{\partial w} ?w?z? 值就是什么
Backward pass
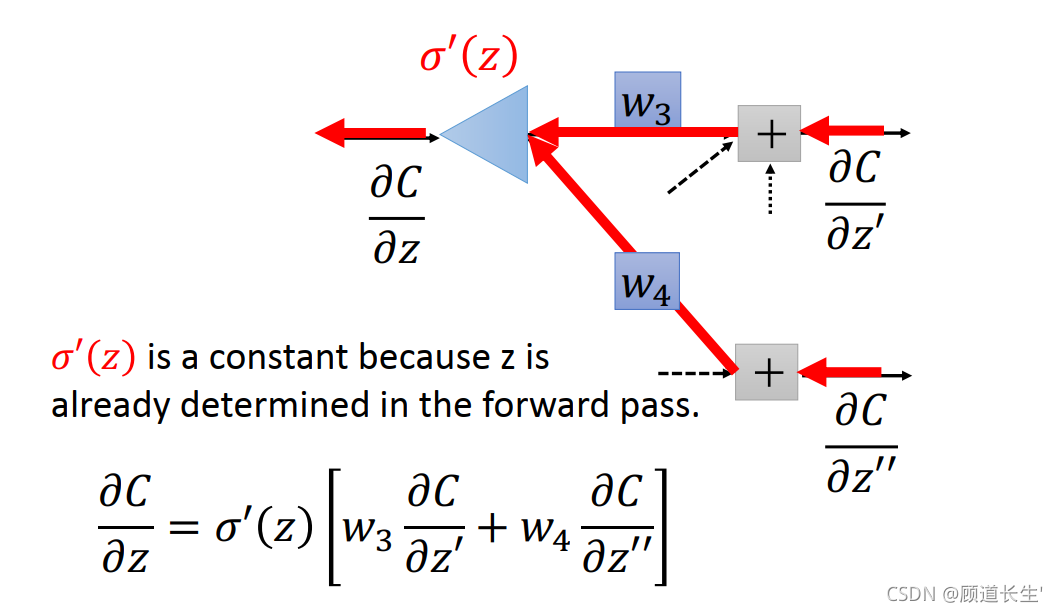
从右往左开始计算
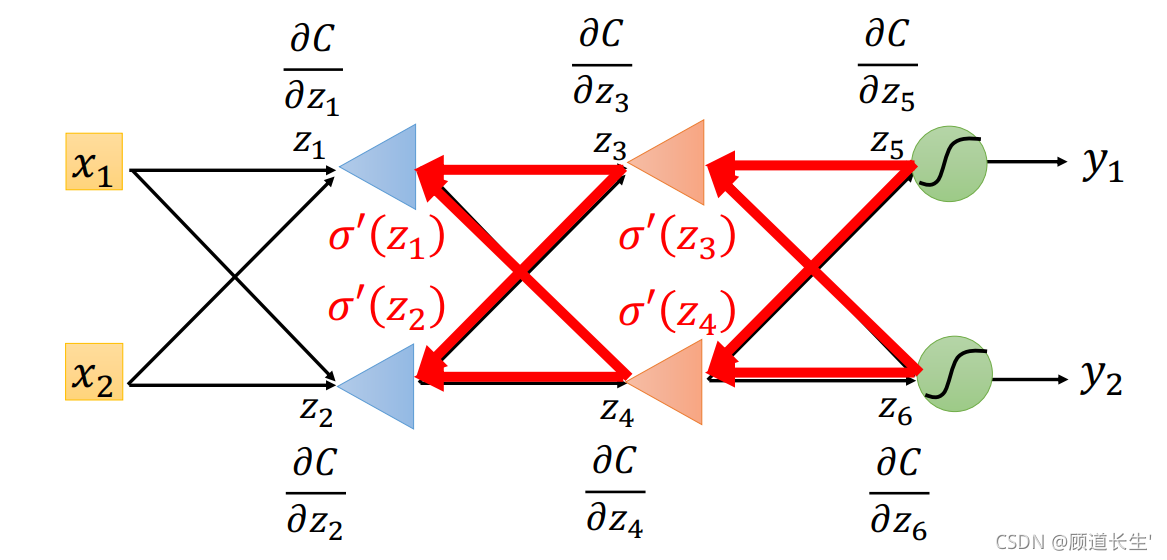
op-amp
这里每一个op-amp的放大系数就是
σ
′
(
z
1
)
,
σ
′
(
z
2
)
,
σ
′
(
z
3
)
,
σ
′
(
z
4
)
\sigma^{\prime}\left(z_{1}\right), \sigma^{\prime}\left(z_{2}\right), \sigma^{\prime}\left(z_{3}\right), \sigma^{\prime}\left(z_{4}\right)
σ′(z1?),σ′(z2?),σ′(z3?),σ′(z4?), 所以整一个流程就是,先快速地计算出
?
C
?
z
5
\frac{\partial C}{\partial z_{5}}
?z5??C? 和
?
C
 ̄
?
z
6
\frac{\partial \underline{C}}{\partial z_{6}}
?z6??C??, 然后再把这两个偏微分的值乘上路径上的weight汇集到neuron上面,再通过op-amp的放大,就可以得到
?
C
?
z
3
\frac{\partial C}{\partial z_{3}}
?z3??C? 和
?
C
?
z
4
\frac{\partial C}{\partial z_{4}}
?z4??C? 这两个偏微分的值,再让它们乘上一些weight, 并且通过一个op-amp,就得到
?
C
?
z
1
\frac{\partial C}{\partial z_{1}}
?z1??C? 和
?
C
?
z
3
\frac{\partial C}{\partial z_{3}}
?z3??C? 这两个偏微分的值,这样就计算完了,这个步骤, 就叫做Backward pass
在做Backward pass的时候,实际上的做法就是建另外一个neural network, 本来正向neural network里面的 activation function都是sigmoid function, 而现在计算Backward pass的时候,就是建一个反向的neural network,它的activation function就是一个运算放大器op-amp, 每一个反向neuron的input是loss
l
l
l 对后面一层 layer的
z
z
z 的偏微分
?
l
?
z
′
\frac{\partial l}{\partial z^{\prime}}
?z′?l?, output则是loss
l
l
l 对这个neuron的
z
z
z 的偏微分
?
l
?
z
\frac{\partial l}{\partial z}
?z?l?, 做Backward pass就是通过这样一个反向 neural network的运算, 把loss
l
l
l 对每一个neuron的
z
z
z 的偏微分
?
l
?
z
\frac{\partial l}{\partial z}
?z?l? 都给算出来
注:如果是正向做Backward pass的话,实际上每次计算一个 ? l ? z \frac{\partial l}{\partial z} ?z?l?, 就需要把该neuron后面所有的 ? l ? z \frac{\partial l}{\partial z} ?z?l? 都给计算一 遍,会造成很多不必要的重复运算,如果写成code的形式, 就相当于调用了很多次重复的函数;而如果是反向做 Backward pass,实际上就是把这些调用函数的过程都变成调用“值"的过程,因此可以直接计算出结果,而不需要 占用过多的堆栈空间
Backpropagation – Summary
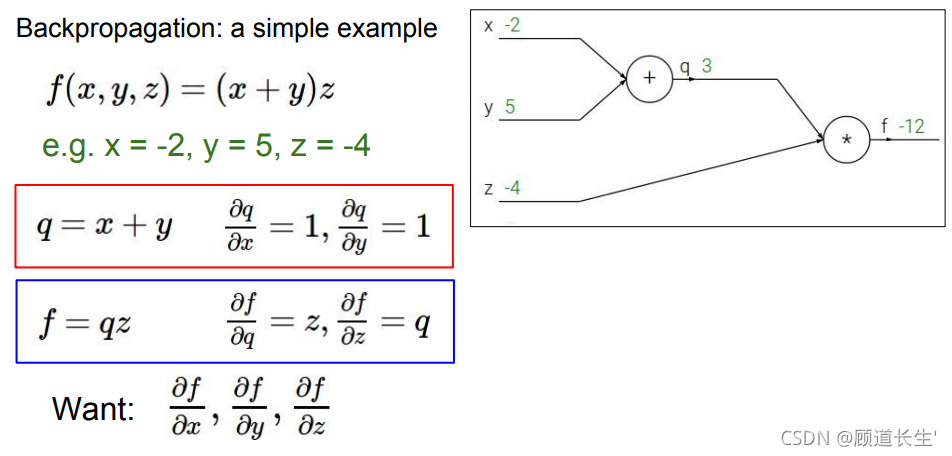
反向传播斯坦福例子:
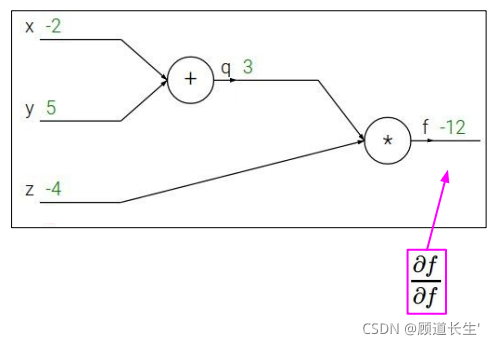
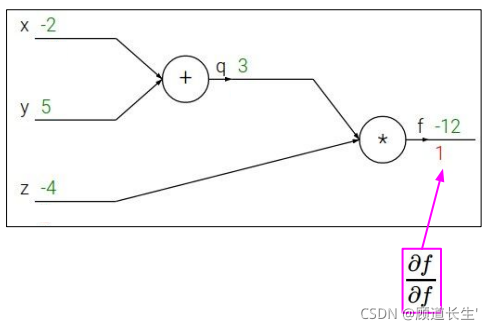
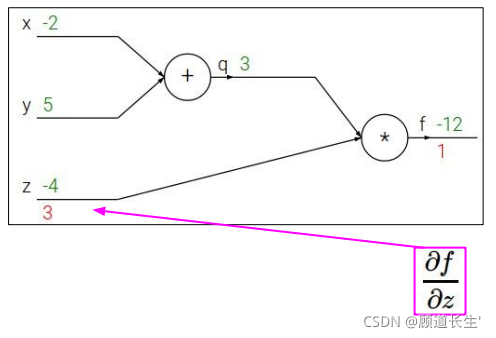
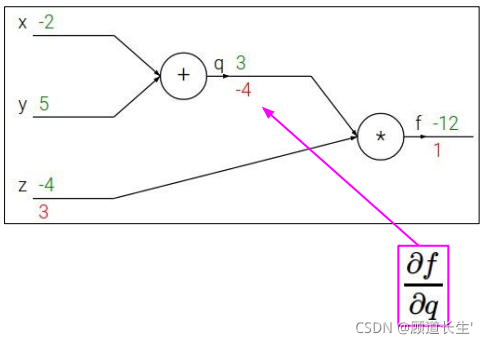
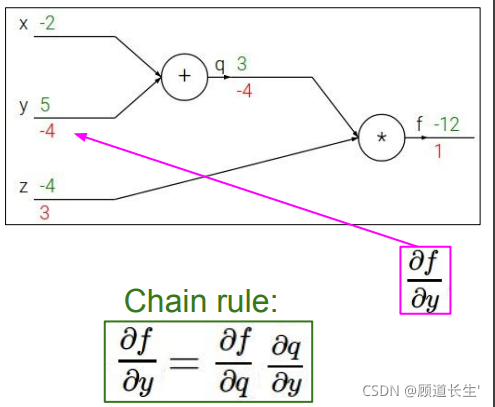
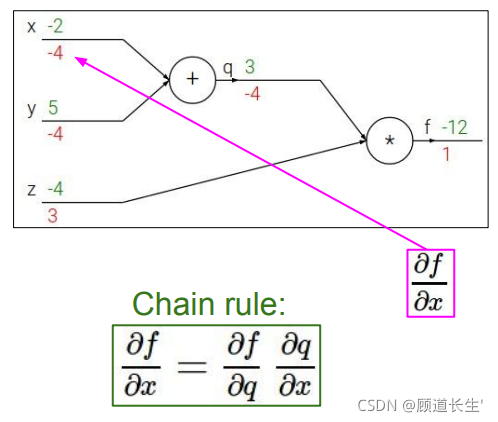
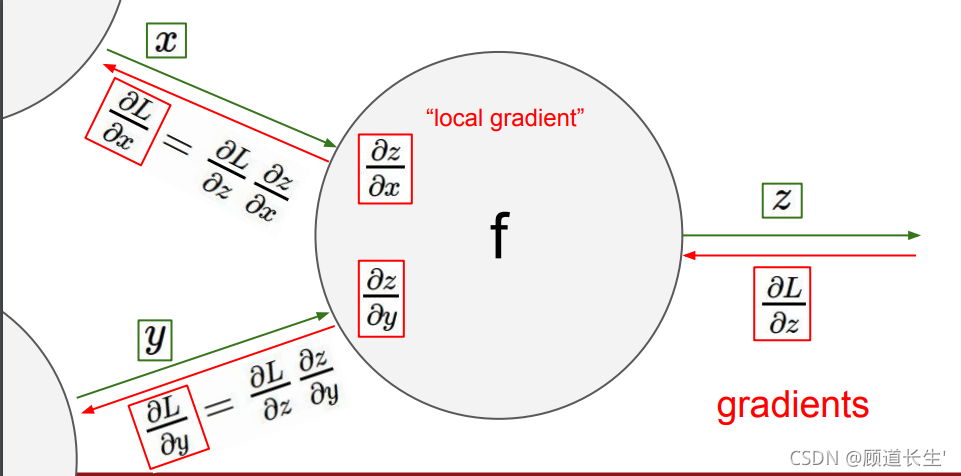
代码实现
简单实现了加法计算图
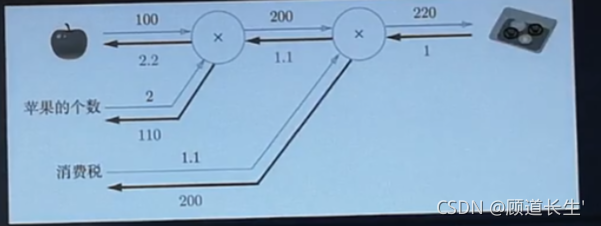
import numpy as np
class MulLayer:
def __init__(self):
self.x = None
self.y = None
def forward(self,x,y):
self.x = x
self.y = y
out = x * y
return out
def backward(self,dout):#dout为上一层的导数
dx = dout * self.y
dy = dout * self.x
return dx,dy
apple = 100
apple_num = 2
tax = 1.1
mul_apple_layer = MulLayer()
mul_tax_layer = MulLayer()
#forward
apple_price = mul_apple_layer.forward(apple,apple_num)
price = mul_tax_layer.forward(apple_price,tax)
#backward
dprice = 1
dapple_price,dtax = mul_tax_layer.backward(dprice)
dapple,dapple_num = mul_apple_layer.backward(dapple_price)
print("price:",int(price))
print("dApple:",dapple)
print("dApple_num:",int(dapple_num))
print("dTax:",dtax)
price: 220 dApple: 2.2 dApple_num: 110 dTax: 200