开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 人工智能 -> PyTorch 入坑十一：损失函数、正则化----深刻剖析softmax+CrossEntropyLoss -> 正文阅读

[人工智能]PyTorch 入坑十一：损失函数、正则化----深刻剖析softmax+CrossEntropyLoss

概念

Loss Function

计算一个样本的损失：
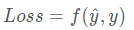
在这里插入图片描述

Cost Function

整个训练集（或者batch）的损失平均值
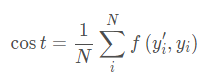
在这里插入图片描述

Objective Function

目标函数是一个更广泛的概念，在机器学习中，目标函数包含Cost和Regularization（正则项）：
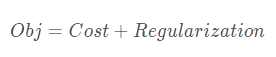
在这里插入图片描述

正则化：惩罚较大的参数，参数的值越小，通常对应于越光滑的函数，也就是更加简单的函数。因此就不易发生过拟合的问题。
常用的有L1正则化和L2正则化
L1更适用于更适用于特征选择；L2更适用于防止模型过拟合
更多细节参考正则化的描述

正则化

方差的概念参考：方差

正则化策略的目的就是降低方差，减小过拟合的发生。

常用的手段有：L1正则化、L2正则化、Dropout、提前终止(早停)、数据扩增。
正则化这个话题比较大，待开一篇文章专门描述。

损失函数

交叉熵损失函数nn.CrossEntropyLoss()

交叉熵损失函数常常用于分类任务
交叉熵是衡量两个概率分布之间的差异。所以交叉熵值越低表示两个分布越近

自信息

自信息用于衡量单个事件的不确定性，其公式为：
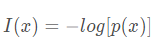
在这里插入图片描述

熵(信息熵)

熵指的是信息熵，是自信息的期望。用来描述一个事件的不确定性，一个事件越不确定熵越大。熵是整个概率分布的不确定性，用来描述整个概率分布
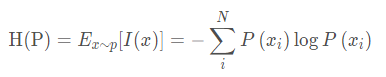
在这里插入图片描述
伯努利分布的信息熵：

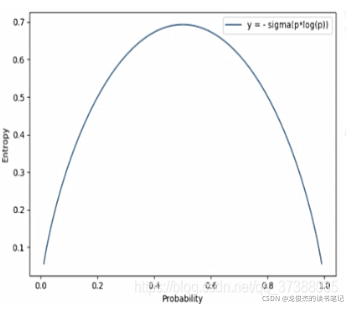
当事件的概率为0.5(如抛硬币)时，其信息熵最大，这也表示事件的不确定性最大，其熵最大值为0.69；如事件“明天太阳从东方生气”（概率极大），其信息熵比较小

相对熵（KL散度）

相对熵也称为KL散度，相对熵用于衡量两个分布之间的差异，也就是两个分布之间的距离，虽然相对熵可以计算两个分布之间的距离，但是相对熵不是一个距离函数，因为距离函数具有对称性，对称性指的是P到Q的距离等于Q到P的距离，但是相对熵不具备距离函数的对称性。

交叉熵

交叉熵、KL散度、信息熵的关系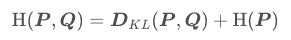： 在这里插入图片描述
公式中的P是真实的概率分布，也就是训练集中样本的分布，Q是模型输出的分布，因为训练集是固定的，所以H ( P ) 是一个常数，所以交叉熵在优化的时候是优化相对熵。
下面看两个交叉熵具体计算的例子：
参考交叉熵损失函数

二分类

在这里插入图片描述

多分类

在这里插入图片描述

学习过程

交叉熵损失函数经常用于分类问题中，特别是在神经网络做分类问题时，也经常使用交叉熵作为损失函数。此外，由于交叉熵计算中需要输入属于某一类的概率，所以交叉熵几乎每次都和sigmoid(或softmax)函数一起出现。
我们用神经网络最后一层输出的情况，来看一眼整个模型预测、获得损失和学习的流程：

神经网络最后一层得到每个类别的得分scores
该得分经过sigmoid(或softmax)函数获得概率输出；
模型预测的类别概率输出与真实类别的one hot形式进行交叉熵损失函数的计算。

同MSE(Mean Squared Error)相比的优势

首先来看sigmoid+MSE的缺点：
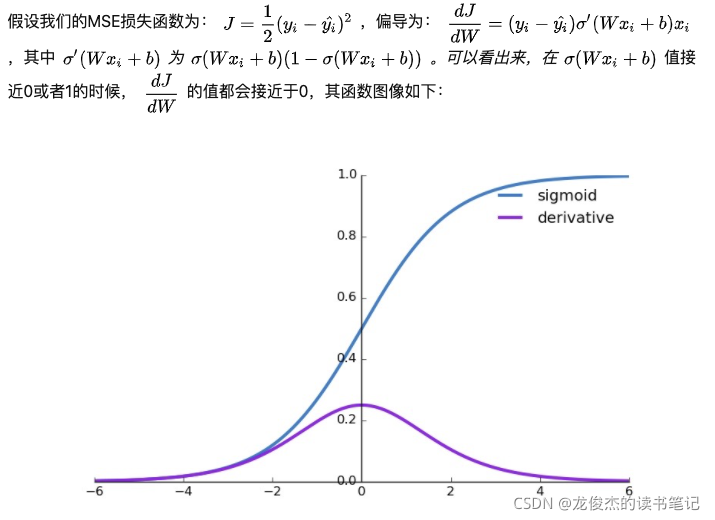
在这里插入图片描述

一句话总结：分类问题中，使用sigmoid/softmx得到概率，配合MSE损失函数时，采用梯度下降法进行学习时，会出现模型一开始训练时，学习速率非常慢的情况
具体来说，在sigmoid层的的输入较大或者较小时，激活函数输出接近于1或者0，导致Loss相对于W的梯度接近0，学习困难。

sigmoid+ CELoss的优点
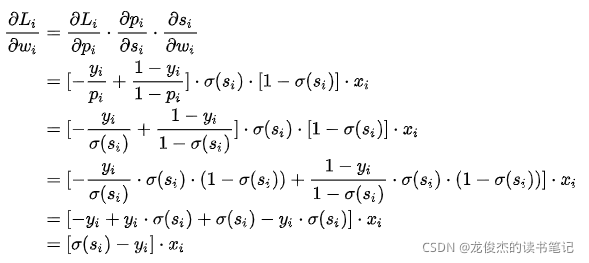
在这里插入图片描述
如公式所示，Loss关于最后一层的w梯度中，si表示sigmoid的输入，yi为label，xi为sigmoid之前的全连接层的输入。
xi -> 全链接层 -> si -> sigmoid层 -> CEloss层。
公式表明，当激活函数层的输出同label差异较大时，L关于w的梯度会较大，从而快速学习。[同生活中“因为明显的犯错可以快速地学习到正确的东西”比较一致]

工程实现中的问题与措施

softmax自身导致的数值问题
Softmax loss = softmax和交叉熵(cross-entropy loss)loss组合而成。
所以全称是softmax with cross-entropy loss。
在caffe，tensorflow等开源框架的实现中，直接将两者放在一个层中，而不是分开不同层，可以让数值计算更加稳定，因为正指数概率可能会有非常大的值
参考 softmax数值稳定性 softmax数值稳定性2

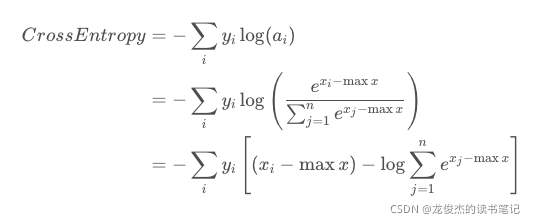
在这里插入图片描述

softmax的缺点

前面说到，softmax一般配合CEloss一起使用。但是softmax这个操作具体什么含义呢。

softmax与hardmax

在CNN的分类问题中，我们的ground truth是one-hot形式，下面以四分类为例，理想输出应该是（1，0，0，0），或者说（100%，0%，0%，0%），这就是我们想让CNN学到的终极目标。
网络输出的幅值千差万别，输出最大的那一路对应的就是我们需要的分类结果。通常用百分比形式计算分类置信度，最简单的方式就是计算输出占比，这种最直接最最普通的方式，相对于soft的max，在这里我们把它叫做hard的max。
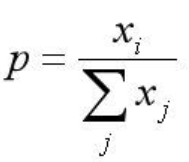
在这里插入图片描述
而现在通用的是soft的max，将每个输出x非线性放大到exp(x)

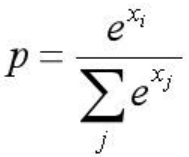
这样做有什么区别呢，看下面的例子：

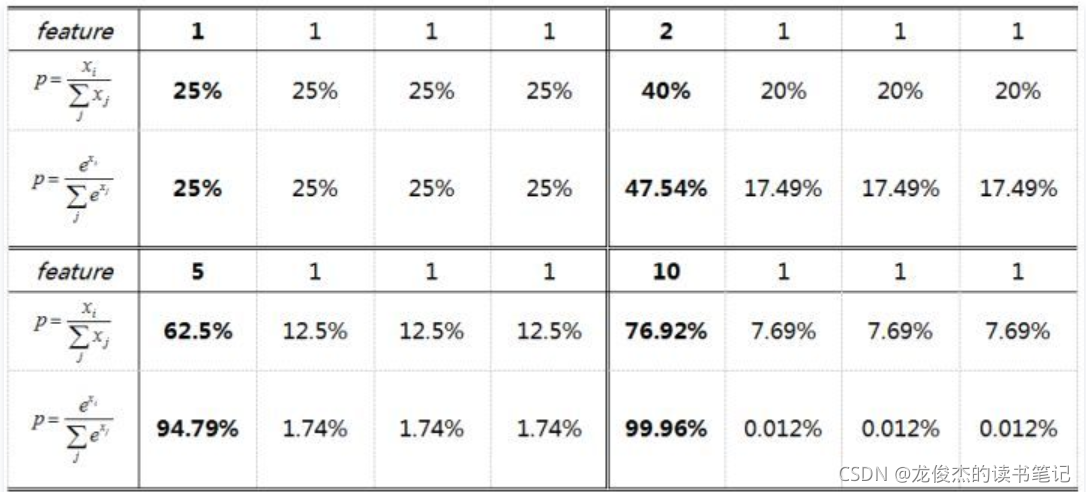
相同输出特征情况，soft max比hard max更容易达到终极目标one-hot形式，或者说，softmax降低了训练难度，使得多分类问题更容易收敛。同时Softmax鼓励真实目标类别输出比其他类别要大，但并不要求大很多。对于人脸识别的特征映射（feature embedding）来说，Softmax鼓励不同类别的特征分开，但并不鼓励特征分离很多，如上表（5，1，1，1）时loss就已经很小了，此时CNN接近收敛梯度不再下降。

Softmax训练的深度特征，会把整个超空间或者超球，按照分类个数进行划分，保证类别是可分的，这一点对多分类任务如MNIST和ImageNet非常合适，因为测试类别必定在训练类别中。封闭集任务有效
但Softmax并不要求类内紧凑和类间分离，这一点非常不适合人脸识别任务，因为训练集的1W人数，相对测试集整个世界70亿人类来说，非常微不足道，而我们不可能拿到所有人的训练样本，更过分的是，一般我们还要求训练集和测试集不重叠。
所以需要改造Softmax，除了保证可分性外，还要做到特征向量类内尽可能紧凑，类间尽可能分离，常见的有L-softmax等