[人工智能]神经网络的激活函数

本文讲解了神经网络中常见的几种激活函数及它们的特点。

我们先来看一下几种常见的激活函数的映射图像：

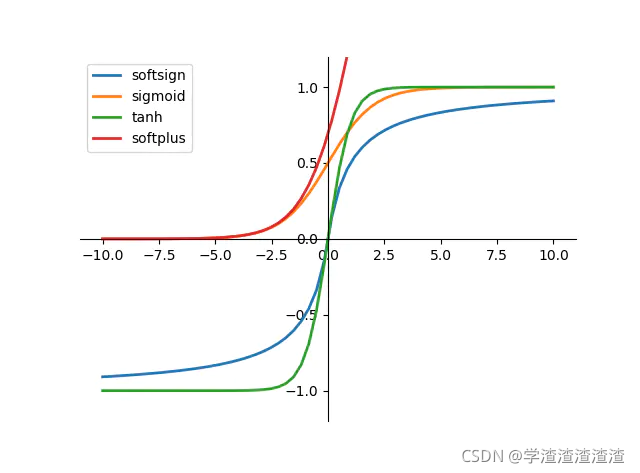
1 sigmoid

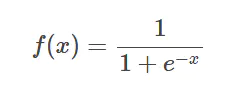
sigmoid函数输出的取值范围是 [0,1]，因此可以将任意区间的值缩放至 [0,1] 范围。

缺点：
在深度神经网络中梯度反向传递时存在梯度爆炸和梯度消失，其发生梯度爆炸发生的概率非常小，而梯度消失发生的概率比较大，下图是其梯度：

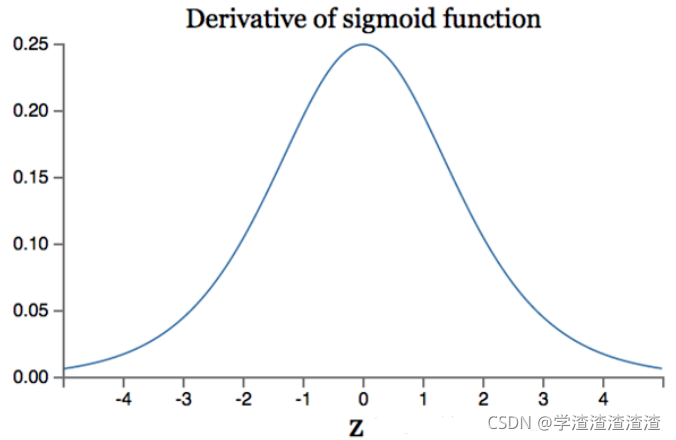
Sigmoid导数取值范围是 [0, 0.25]，由于神经网络反向传播时的“链式反应”，很容易就会出现梯度消失的情况。例如对于一个10层的网络， 根据 $0.25^{10}\approx 0.000000954$ ，第10层的误差相对第一层卷积的参数 $W_1$ 的梯度将是一个非常小的值，这就是所谓的“梯度消失”。所以在深层网络中，要谨慎使用sigmoid激活函数，建议使用sigmoid的网络层数不要超过2~3层。
此外，Sigmoid的输出不是0均值（即zero-centered）；这会导致后一层的神经元将得到上一层输出的非0均值的信号作为输入，随着网络的加深，会改变数据的原始分布。
最重要的是，这种激活函数运算量较大，会降低训练时间。

2 tanh

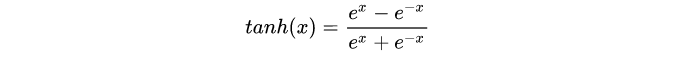
也可以写成这样：

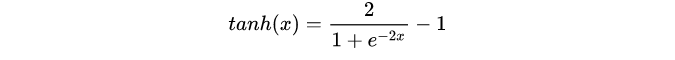
其图像和其导数图像如下图：
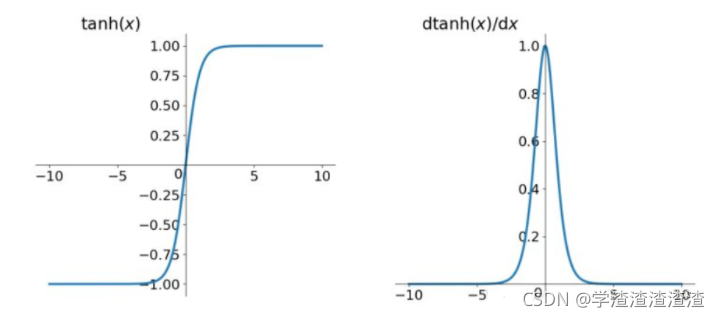tanh它解决了Sigmoid函数的不是zero-centered输出问题（输出均值不为0的问题），然而，梯度消失（gradient vanishing）的问题和幂运算的问题仍然存在。

3 Relu

$relu(x)=max(0,x)$

看看它和它导数的图像：

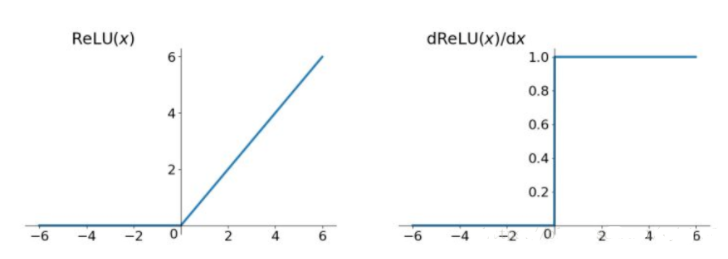
优点：
1） 解决了梯度消失问题 (在正区间)
2）计算速度非常快，只需要判断输入是否大于0
3）收敛速度远快于sigmoid和tanh。
但是其也有缺点：
1）ReLU的输出不是zero-centered
2）Dead ReLU Problem，指的是某些神经元可能永远不会被激活，导致相应的参数永远不能被更新。有两个主要原因可能导致这种情况产生: (1) 非常不幸的参数初始化，这种情况比较少见 (2) learning rate太高导致在训练过程中参数更新太大，不幸使网络进入这种状态。解决方法是可以采用Xavier初始化方法，以及避免将learning rate设置太大或使用adagrad等自动调节learning rate的算法。

我们来分析一下它的导数特点
ReLU在x>0下，导数为常数1的特点：
导数为常数1的好处就是在“链式反应”中不会出现梯度消失，但梯度下降的强度就完全取决于权值的乘积，这样就可能会出现梯度爆炸问题。解决这类问题：一是控制权值，让它们在（0，1）范围内；二是做梯度裁剪，控制梯度下降强度，如ReLU(x)=min(6, max(0,x))

ReLU在x<0下，输出置为0的特点：
描述该特征前，需要明确深度学习的目标：深度学习是根据大批量样本数据，从错综复杂的数据关系中，找到关键信息（关键特征）。换句话说，就是把密集矩阵转化为稀疏矩阵，保留数据的关键信息，去除噪音，这样的模型就有了鲁棒性。ReLU将x<0的输出置为0，就是一个去噪音，稀疏矩阵的过程。而且在训练过程中，这种稀疏性是动态调节的，网络会自动调整稀疏比例，保证矩阵有最优的有效特征。
针对某个神经单元，若其输出小于0，则其梯度就等于0，从此成为一个 “dead activation”，即该神经元输出永远小于0了。所以该激活函数的最原本的输入应该大于0，不然会丢失很多有效特征

4 Leaky ReLU, PReLU, RReLU

为了防止神经元 “dead” 的情况，后人将x<0部分并没有直接置为0，而是给了一个很小的负数梯度值 $\alpha$。

4.1 Leaky ReLU

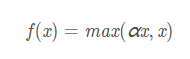
Leaky ReLU中的 $\alpha$ 为常数，一般设置 0.01。这个函数通常比 Relu 激活函数效果要好，但是效果不是很稳定，所以在实际中 Leaky ReLu 使用的并不多。

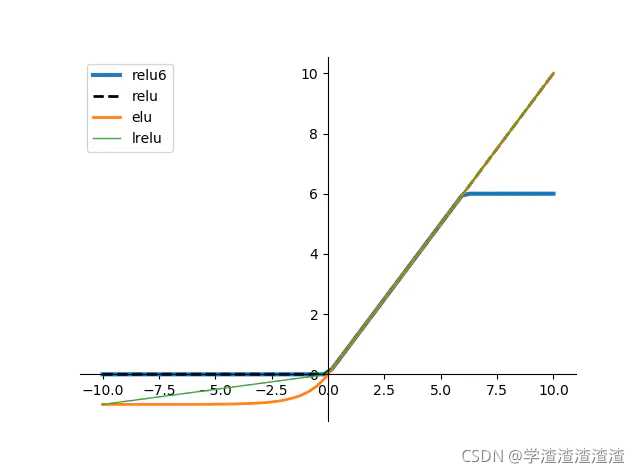
4.2PRelu

PRelu（参数化修正线性单元） 中的 $\alpha$ 作为一个可学习的参数，会在训练的过程中进行更新。

4.3 RReLU

RReLU（随机纠正线性单元）也是Leaky ReLU的一个变体。在RReLU中，负值的斜率在训练中是随机的，在之后的测试中就变成了固定的了。RReLU的亮点在于，在训练环节中，aji是从一个均匀的分布U(I,u)中随机抽取的数值。

参考：
https://blog.csdn.net/tyhj_sf/article/details/79932893
https://zhuanlan.zhihu.com/p/73214810