近邻算法
近邻算法(Affinity Propagation, AP)是Science在2007年发布的聚类算法,但其基本目标和K-means一致,都是追求找出组内距离平方和最小的划分方法。既然目标都一致,已经有了K-means为什么还会出现近邻算法呢?其实很简单,近邻算法有比K-means优秀的地方:近邻算法训练前不需要指定分组数目(K-means算法中的K值);AP算法具有结果稳定可重现,不依赖于开始的随机中心点等优点。虽然这些都优于K-means,但有得必有失,算法的时间复杂度要比K-means高。
近邻算法的理解
从字面上来理解 近邻算法就是“距离”较近,“相邻”的样本点聚为一类(组)。那用什么来判断这些“距离”和“相邻”呢?,下面我们用个例子来理解下近邻算法的概念和判断标准。大学的python程序设计课的期末考试要通过小组来完成,老师要求同学们自行组队,对每组人数没有上限要求,但必须有且仅有一名组长。
这时,同学们纷纷讨论起来了:
张三:李四,我们组队吧,我选你做组长
李四:王五这门课学的好,我觉得应该和他组一队,抱大腿
张三:好吧,我和他有矛盾,合不来,我去问问陈六吧
王五:我虽然这门课学的还可以,但不要选我做组长啊,我不太适合做组长
……
这些讨论无非就两个话题,我希望和谁一组并选谁为组长,我自己是不是想做组长。最终,同学们都能找到合适的组并推选出组长。
如果我们把这一个过程看成聚类过程,而上面的流程正好演绎了近邻算法的分组过程。下面我们要上面的例子来理解下近邻算法的几个概念:
质心:就是每个小组的组长,是聚类中每一组的核心。
参考度:就是每个同学想成为组长的意愿程度,在聚类之前可以对每个成员设置一个参考度值。
相似度:一般记为是(i,k),可以理解为同学i与同学k在讨论前的熟悉程度,如果该值越高,则这两个同学越可能分为一组.在一般的聚类场景中,也就是两个特征向量i,k之间的距离.
责任度:一般记为r(i,k),就是同学i对同学k说的一句话(就是张三对李四说的话),其内容是"我想选你为组长的意愿是多少",如果该值越高,说明i越想加入k的一组.
可用度:一般记为a(i,k),同学k对同学i说的一句话(王五说的话)“我想当组长的意愿是多少”,该值越高,则说明k越可能是质心.
其中质心在聚类完成之后产生(就是同学门分好组后在选组长),参考度和相似度在聚类之前需要给出的超参数责任度和可用度是在聚类过程使用的算法概念.
近邻算法的迭代
近邻算法和K-means算法类似,都是使用迭代的方法逐渐找到质心/中心点.要注意这两个"心"是不同的.K-means算法的中心点可以是特征取值空间上的任意一个点(可以不是数据样本点),而近邻算法的质心必须是样本数据中的某个点 .下面我们来看下近邻算法是怎么迭代的.
数据样本中每两个结点之间都有相应的r(i,k)和a(i,k)因此可以将系统整体的责任度和可信度各自看成一个二维矩阵,近邻算法的迭代目标就是逐步更新责任度和可信度矩阵.每个迭代过程可以分问两步执行:
第一步:更新责任度矩阵:每个r(i,k)新的值等于原始相似度s(i,k)减去上一轮迭代I结点收到的最大"相似度+可用度"组合(注意:第一轮迭代所以结点的可用度为零).可以理解为"如果有其他结点更愿意做质心,则结点i发给k的责任度降低".
第二步:更新可用度矩阵:每个a(i,k)新的值等于其自责任a(i,k)加上其他结点发给k的所有正向责任度和.可以理解为"有越多的结点希望k做质心,则其越自告奋勇的当质心"
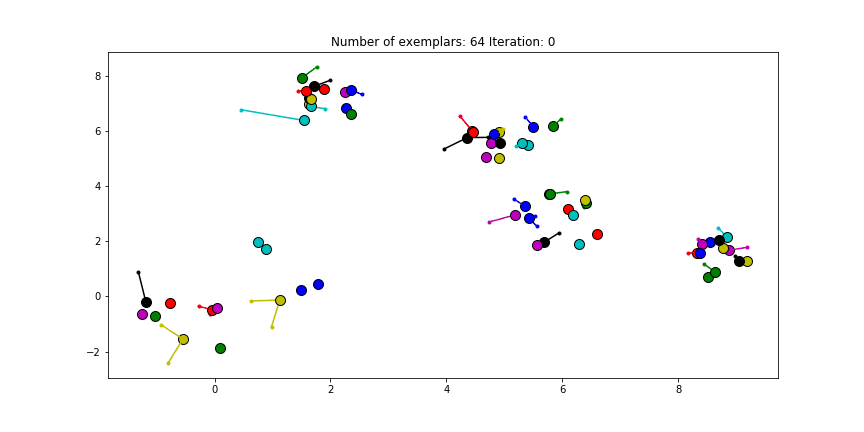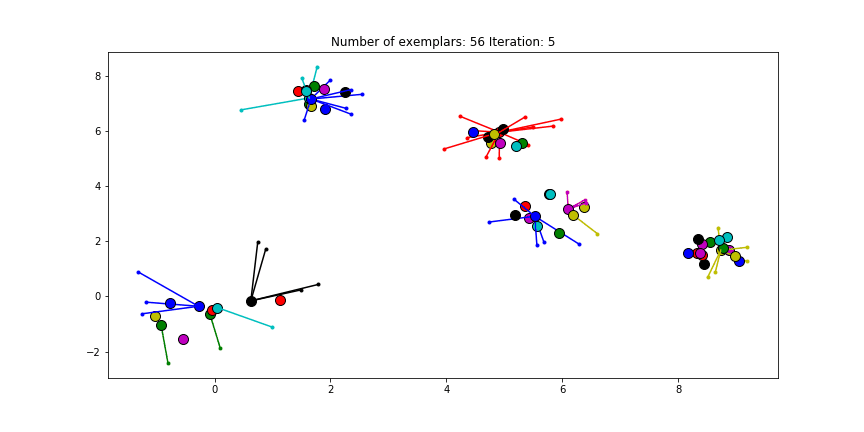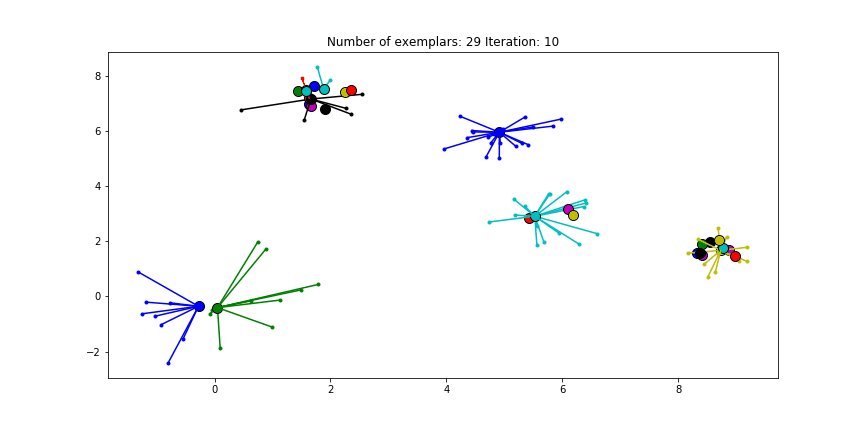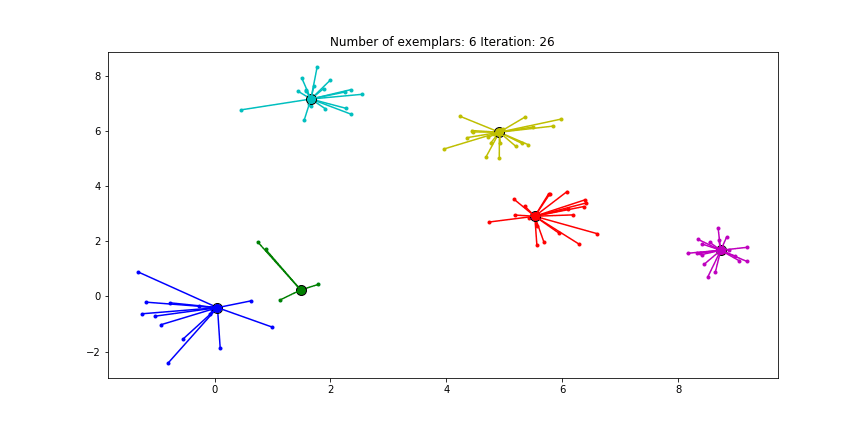
每一轮迭代其实都是一个聚类结果的瞬间状态.在该状态中将责任矩阵与可用度矩阵相加,则对于每个结点i来能够获得r(i,k)和a(i,k)最大值的那个k结点就是i所在组的质心.该迭代过程的收敛停止条件可以达到最大迭代次数,或者连续若干次迭代聚类结果没有发生变化.下面的动态图就是近邻算法的迭代过程和聚类结果.
近邻算法实战
from sklearn.cluster import AffinityPropagation
import matplotlib.pyplot as plt
import numpy as np
import random
# 创建训练数据
data = [[random.randint(1, 4) for j in range(1, 3)] for i in range(1, 51)]
print(data)
# preference=-5的分组结果
af = AffinityPropagation(preference=-5) # 引入AP算法
af.fit(data)
print('preference=-5:')
print(af.labels_) # 查看聚类结果
# preference=-10的分组结果
af = AffinityPropagation(preference=-10)
af.fit(data)
print('preference=-10:')
print(af.labels_)
# preference=-20的分组结果
af = AffinityPropagation(preference=-20)
af.fit(data)
print('preference=-20:')
print(af.labels_)
运行结果:
训练数据:
[[3, 3], [3, 2], [2, 3], [3, 2], [1, 4], [1, 1], [4, 2], [3, 2], [4, 4], [2, 2], [2, 1],
[2, 4], [4, 3], [3, 4], [1, 3], [1, 4], [1, 2], [3, 4], [1, 3], [4, 3], [1, 3], [2, 3],
[3, 1], [3, 4], [2, 1], [3, 3], [2, 2], [2, 2], [1, 4], [3, 3], [4, 4], [1, 1], [4, 1],
[1, 1], [3, 2], [3, 3],[2, 2], [1, 3], [2, 4], [4, 1], [3, 1], [2, 2], [3, 3], [4, 1],
[4, 1], [4, 4], [4, 4], [4, 3], [1, 4], [3, 3]]
preference=-5:
[3 0 3 0 1 0 4 3 2 0 0 1 2 3 1 1 0 2 1 3 1 3 4 3 0 3 0 0 1 3 2 0 4 0 0 3 0
1 1 4 4 0 3 4 4 2 2 2 1 3]
preference=-10:
[0 2 1 2 1 1 2 2 0 2 2 0 0 0 1 1 1 0 1 0 1 1 2 0 2 0 1 1 1 0 0 2 2 2 2 0 1
1 0 2 2 1 0 2 2 0 0 0 1 0]
preference=-20:
[2 1 1 1 3 1 0 0 2 1 1 2 0 2 3 3 1 2 3 0 3 1 0 2 1 2 1 1 3 2 2 1 0 1 0 2 1
3 2 0 0 1 2 0 0 2 2 0 3 2]
Process finished with exit code 0
代码中对相同的数据集用不同的preference参数进行了3次聚类,获得了不同的聚类结果.preference=-5聚类划分了5个组,preference=-10聚类划分了3个组,preference=-20聚类划分了4个组.
下面总结一些比较重要的初始化参数和属性
| 参数 | 解析 |
|---|---|
| damping | 阻尼因子,范围在0.5-1之间,该值越大每次迭代中责任度矩阵和可用度矩阵更新变慢,因此算法收敛也变慢.但较大的阻尼因子可以防止这些值在更新中的抖动,降低无法收敛的风险. |
| convergence_iter | 聚类结果连续convergence_iter次迭代没有变化时,认为已经达到稳定,算法完成 |
| max_iter | 算法的最大迭代次数 |
| preference | 结点参考度,可以是一个数值(所有样本数据使用相同的参考度),也可以是一个数组(每个样本数据有不同的参考度) |
| affinity | 相似度计算方法,可以是euclidean或precomputed.前者是默认值. |
| 属性 | 解析 |
|---|---|
| cluster_centers_indices_ | 质心样本在训练集中的索引 |
| cluster_centers_ | 质心结点的特征向量数组 |
| labels | 训练样本的聚类结果 |
| affinity_matrix_ | 近邻矩阵,也就是责任度矩阵与可用度矩阵和 |
| n_iter_ | 算法收敛所用的迭代次数 |