学习目的
为了能够对湍流相干结构进行分析。
学习过程
1.Wavelets and Multiresolution Analysis By Steve Brunton
一个思路是,对于频率更低的信号,由于其变化更慢,可以用更粗的时间精度来分辨。因此,可以采用不同精度来分析不同频率的信号
mother wavelets 某种形状的基准小波。然后可以进行伸缩和相位变换。生成的函数依然是正交的(类似三角级数)
ψ
a
,
b
(
t
)
=
1
a
ψ
(
t
?
b
a
)
\psi_{a,b} (t)=\frac{1}{\sqrt{a}}\psi(\frac{t-b}{a})
ψa,b?(t)=a?1?ψ(at?b?)
小波变换
2.Easy Introduction to Wavelets By Simon Xu
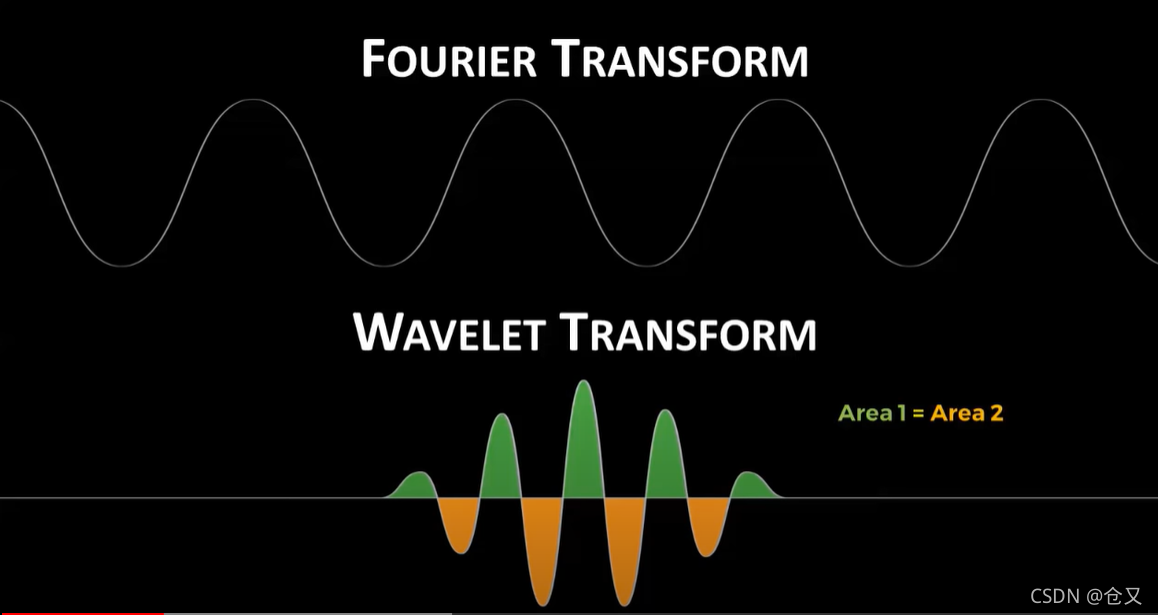
傅里叶变换是采用一系列三角函数来逼近原函数,但小波分析则是利用一系列小波(wavelets).小波需要具有正值的积分和负值的积分相加为0(上部分面积等于下部分面积)

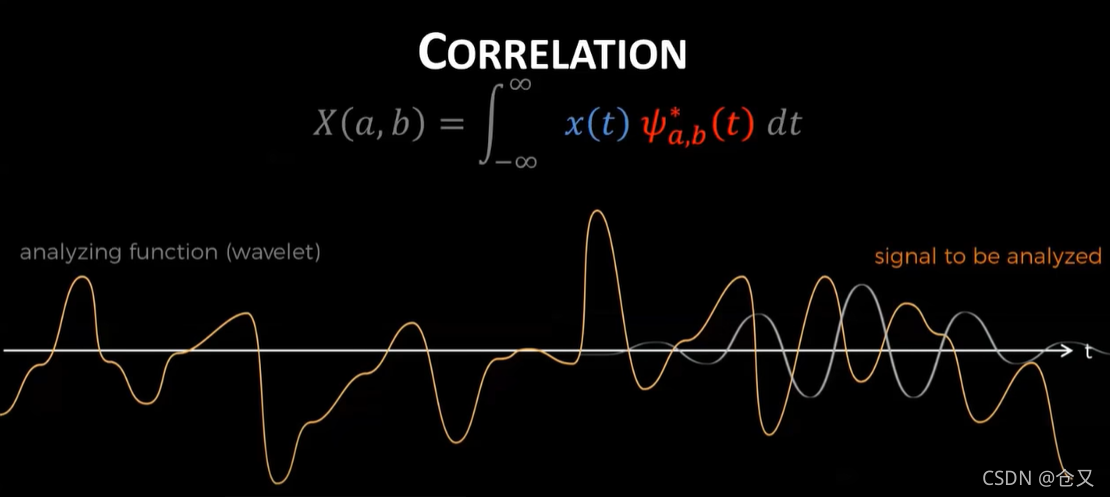
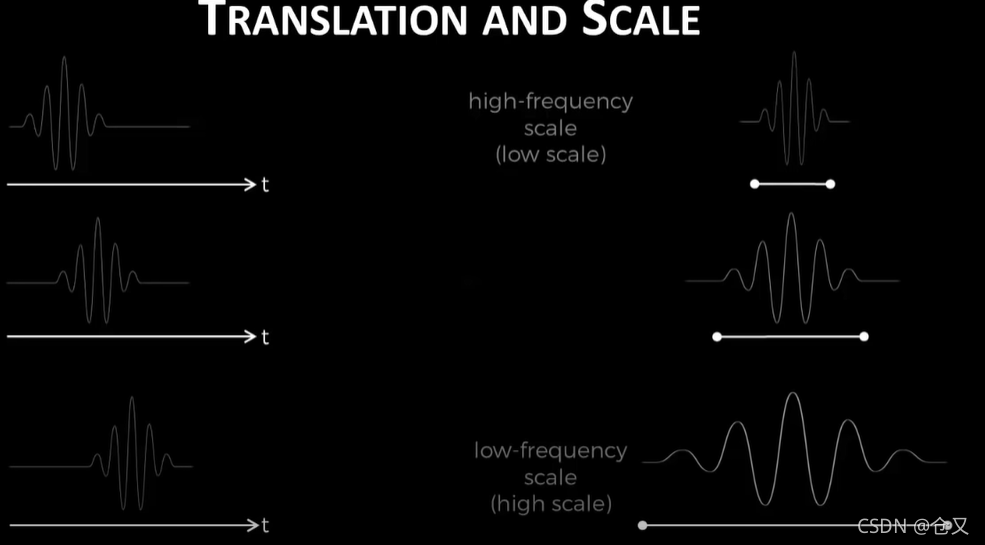
小波变换和傅里叶变换相似,只不过基函数变成了小波函数。然后傅里叶变换后是得到不同频率的赋值,而小波变换则是得到尺度(scale)和偏移(translation).也就是之前说的不同的伸缩和相位。对于low scale,则频率更高,high scale频率更低。
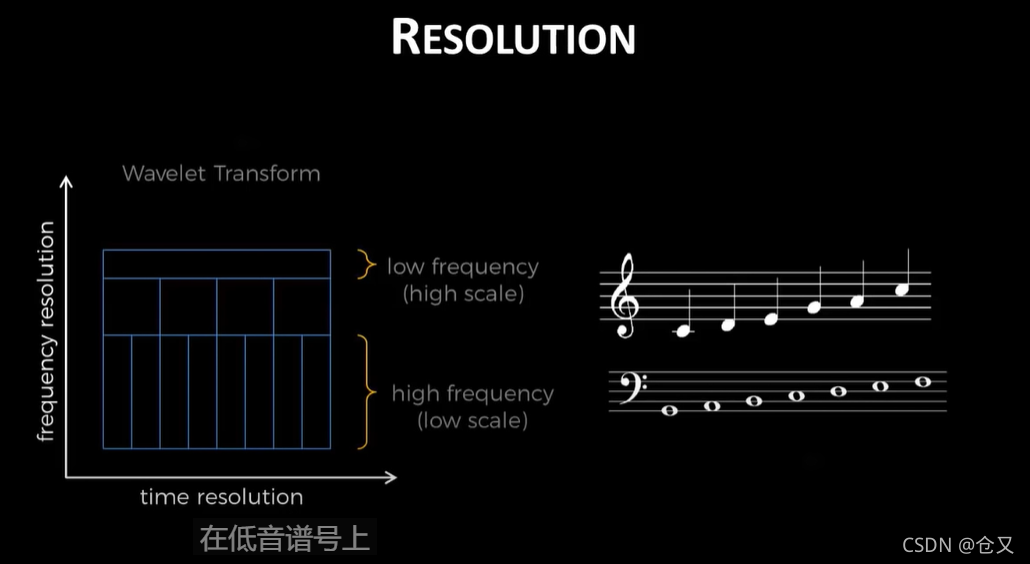
小波变换用于解决频域和时域的分辨率问题。他讲到,海森堡原理指出,我们对某个位置的判别不可能在时域和频域中同时都达到很高的精度。
左边这张图估计是说因为海森堡原理,每个格子要保持一样的面积,当时间分辨率很高的时候,频域上的精度就会下降(?)
就类似于我们大脑在处理音乐。音阶的频率并不是线性增长的,每升一个八度,频率会翻一倍。可能也是因为我们大脑对于越高的音符(频率越大),分辨微小频率间差异的能力已经降低了。而对于低音,我们则需要更长的时间来分辨音符,则我们一般用更长的时间来弹奏低音谱号上的音符(!!!这一段简直太有意思了,想想谱子确实这么一回事,原来还可以这么来解释!!!)
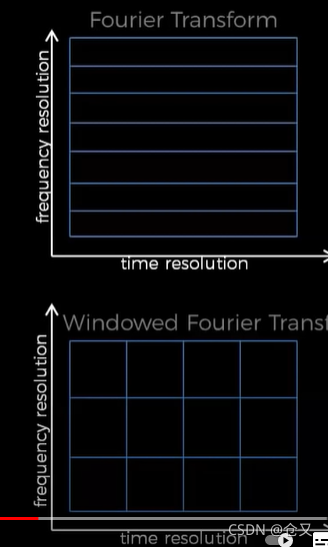
对于傅里叶变换,在时间上不具有分辨率,但对频率有很高的分辨率。而加窗傅里叶变换,则通过减少一些频率上的分辨率来增加时间上的分辨率。

Vanishing Moments的概念:用来区分不同类型的小波,如果Vanishing Moments(k)越大的话,则代表小波函数越复杂,越能够准确表达复杂信号。但如果消失距越大的话,则代表longer support(什么意思?计算量更大吗?) 。同时,消失距为p的话,那么p阶以前的信号不会被识别
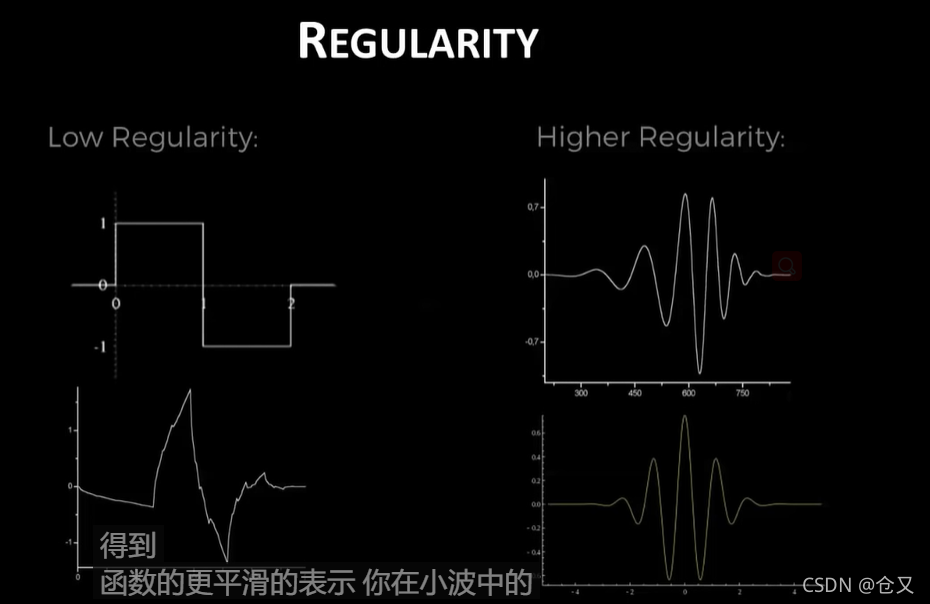
规律性更高的小波得到的函数更光滑
3.Ingrid Daubechies: Wavelet bases: roots, surprises and applications
Ingrid Daubechies,是图像压缩小波变换领域的鼻祖。
This lecture was held by Ingrid Daubechies at The University of Oslo, May 24, 2017 and was part of the Abel Prize Lectures in connection with the Abel Prize Week celebrations.
讲座先放了一张梵高自画像(黑白),然后因为每个像素都有一个灰度的数值,则图像变成一个矩阵,压缩这个图像就是要把矩阵变小。但如果采取平均的方式,则很容易再边缘处丢失很多细节。因此对原矩阵在水平方向分别进行两个值间的平均和做差操作,得到两个矩阵:
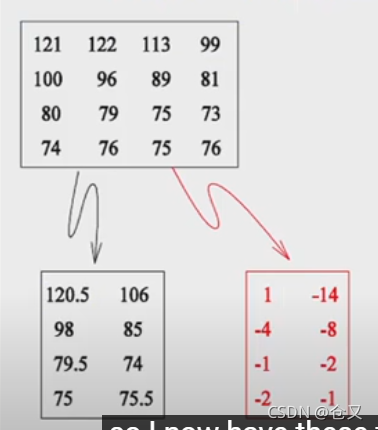
然后对生成的矩阵再在垂向进行同样的操作:
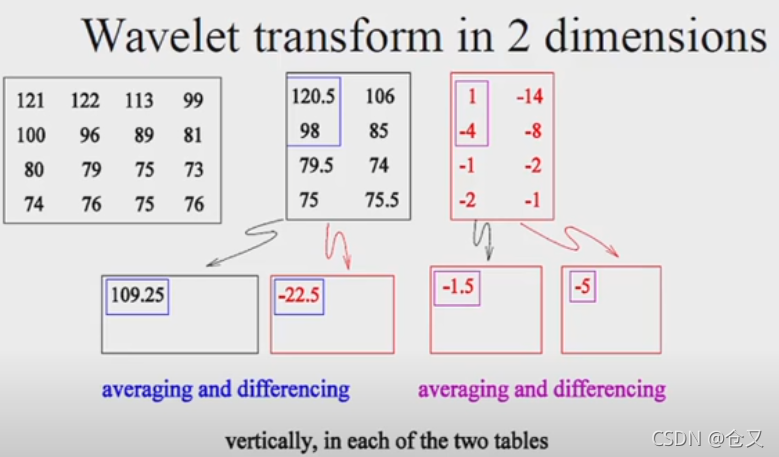
现在得到四个矩阵,且红色的三个矩阵中的较大数值代表着不同方向上的边缘:
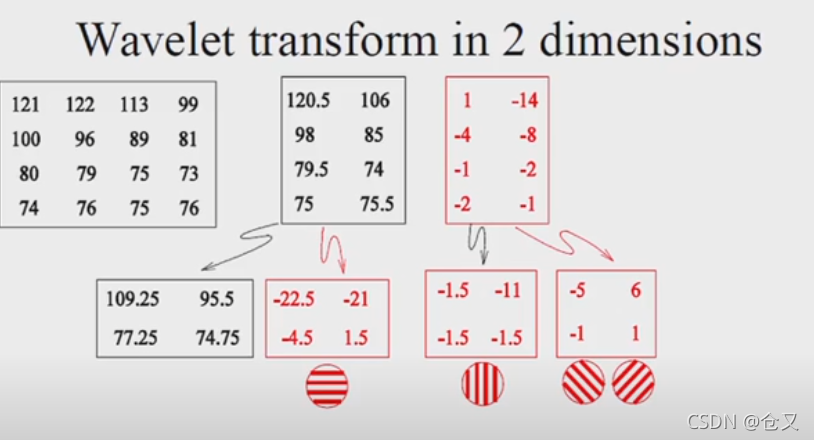
然后对以下图进行处理。左图在水平和竖向都进行平均后,得到右边长度小一半的图(数值是0~255),然后做差后得到的矩阵数值取值范围是[-255,255]。多贝丽用-255代表黑,255代表白,来表示差值图。则得到另外三张图

可发现差值图中的“大值”其实是非常少的。然后继续可以用这种方法不断压缩。最后得到一个很小的图。如果把那个很小的图直接放大,会损失很多细节,但如果不断把那些差值矩阵的信息加进来,就能逐渐还原出原本的图片。需要注意的是,如果对于变化较大的地方,添加差值矩阵信息之后差别会很明显,但如果对于变化不是很大的区域,比如说图片中的天空,那么增加差值矩阵信息就不是很必要。因此就可以根据想要看的区域来选择如何是否需要还原。
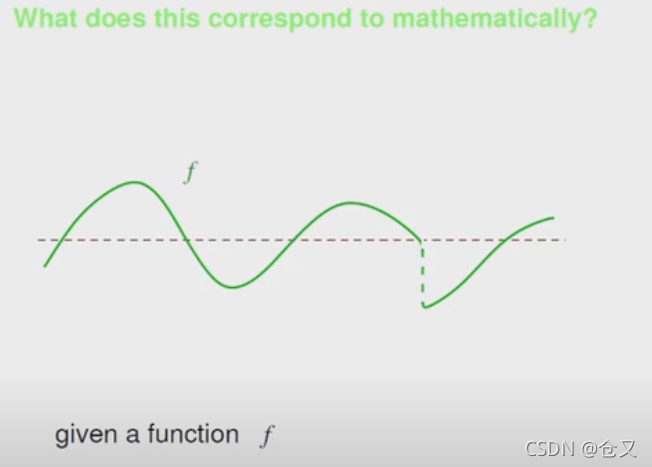
数学表达:
对于一个函数,如果间断点取平均,则间隔越短,越逼近原函数。
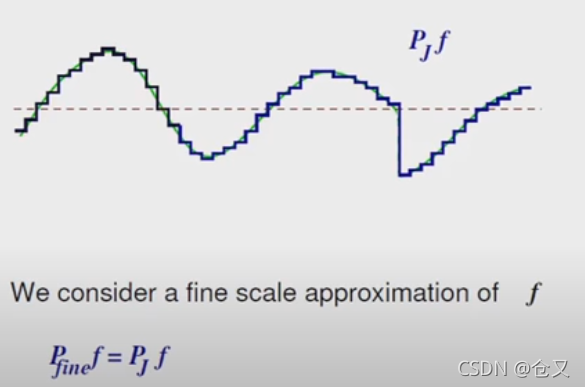
对P_fine在进行平均
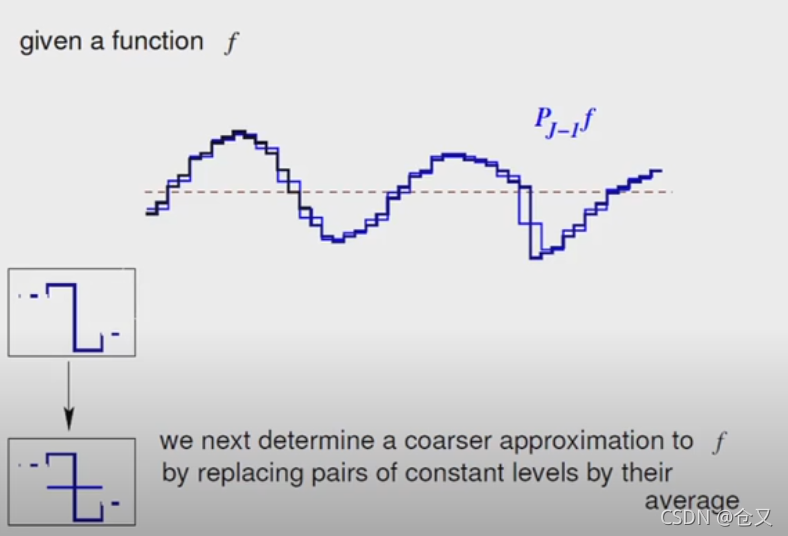
得到:

还可以继续:
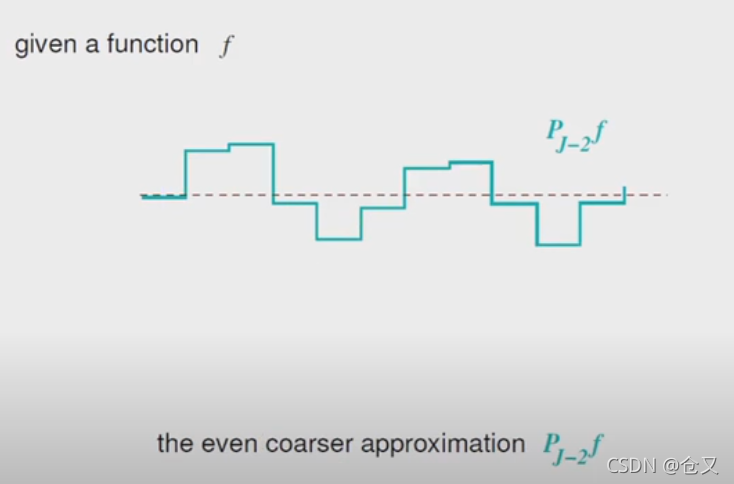
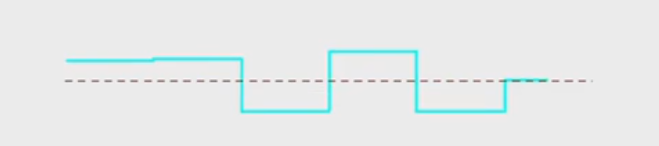
用相邻两个函数的差来表示损失的细节:
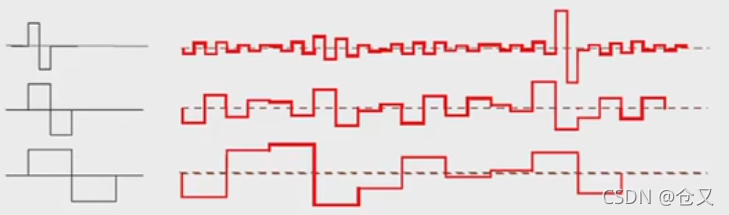
便可见,如果把平均作为一种基函数,则不同尺度的平均则类似用不同缩放比尺的基函数:
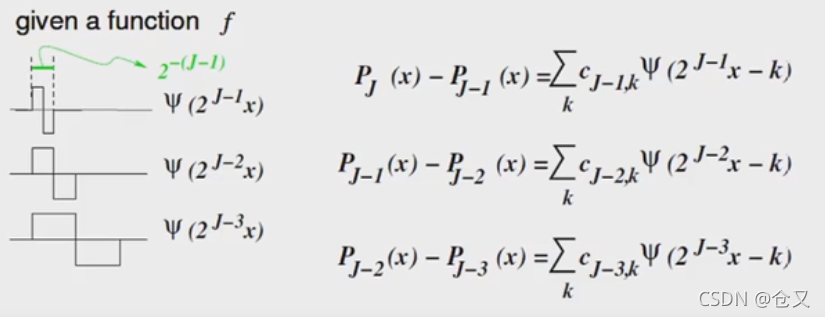
因此,如果把等式右边项全都加起来的话,就可以得到最开始的间断逼近。当这个阶数无穷时,就能接近原函数。然后需要注意的是这一系列小波函数时正交的(就和傅里叶变化很像了?)

小波函数也可换成其他更高阶的近似方案

(这块开始不是很理解了,这些空间不是很明白是指什么空间,向量?函数?)但是后面说说到小波分析可以看局部的信息,而且有一些系数如果很小,把它们变成0不会对原函数有什么影响,但傅里叶变化则不是这样

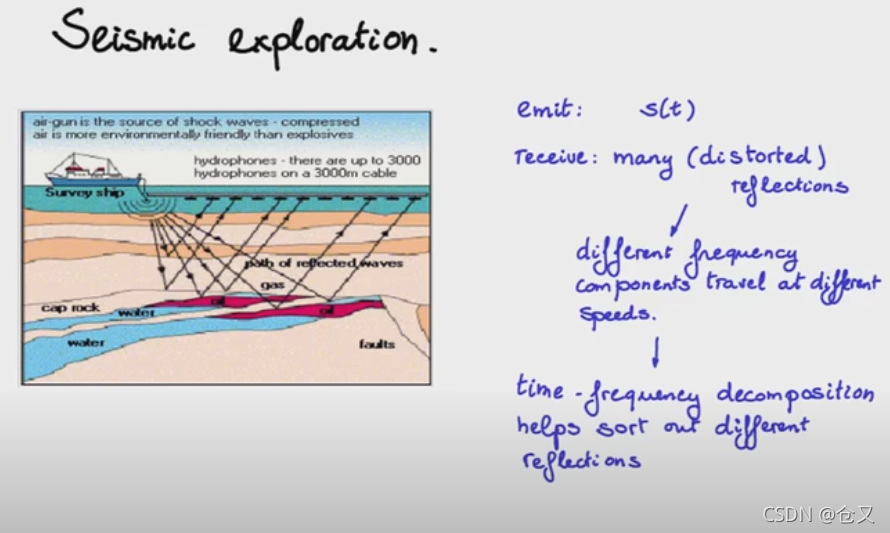
小波的根源:从调和分析、地震探查、量子力学、计算视觉、等路线: