文章目录
1.聚类分析
1.1 无监督学习与聚类算法
决策树、线性和逻辑回归都是比较常用的机器学习算法,他们虽然有着不同的功能,但却都属于“有监督学习”的一部分,即是说,模型在训练的时候,即需要特征矩阵X,也需要真实标签y。机器学习当中,还有相当一部分算法属于“无监督学习”,无监督的算法在训练的时候只需要特征矩阵X,不需要标签。无监督学习的代表算法有聚类算法、降维算法。
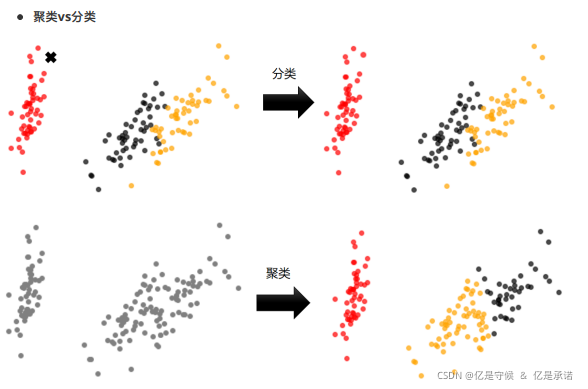
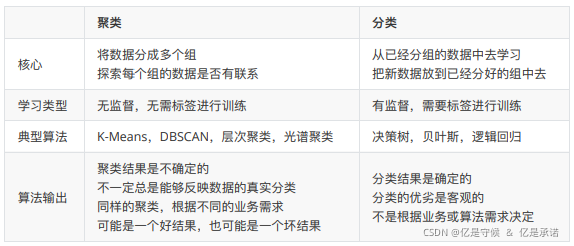
聚类算法是无监督类机器学习算法中最常用的一类,其目的是将数据划分成有意义或有用的组(也被称为簇)。这种划分可以基于我们的业务需求或建模需求来完成,也可以单纯地帮助我们探索数据的自然结构和分布。如果目标是划分成有意义的组,则簇应当捕获数据的自然结构。然而,在某种意义下,聚类分析只是解决其他问题(如数据汇总)的起点。无论是旨在理解还是应用,聚类分析都在广泛的领域扮演着重要角色。这些领域包括:心理学和其他社会科学、生物学、统计学、模式识别、信息检索、机
器学习和数据挖掘。
聚类分析在许多实际问题上都有应用,下面是一些具体的例子,按聚类目的是为了理解数据自然结构还是用于数据处理来组织。
1.1.1.旨在理解数据自然结构的聚类
在对世界的分析和描述中,类,或在概念上有意义的具有公共特性的对象组,扮演着重要的角色。的确,人类擅长将对象划分成组(聚类),并将特定的对象指派到这些组(分类)。例如,即使很小的孩子也能很快地将图片.上的对象标记为建筑物、车辆、人、动物、植物等。就理解数据而言,簇是潜在的类,而聚类分析是研究自动发现这些类的的技术。
1.1.2 用于数据处理的聚类
聚类分析提供由个别数据对象到数据对象所指派的簇的抽象。此外,-些聚类技术使用簇原型(即同一个簇中用于代表其他对象的数据对象,例如质心等)来刻画簇特征。这些簇原型可以用作大量数据分析和数据处理技术的基础。因此,就聚类用于数据处理层面而言,聚类分析是研究发现最有代表性的簇原型的技术。
- 数据降维
许多数据分析技术,如回归和PCA,都具有O(m2 )或更高的时间或空间复杂度(其中m是对象的个数)。因此对于大型数据集,这些技术不切实际。然而,可以将算法用于仅包含簇原型的数据
集,即每一列只保留其原型,而不是整个数据集。依赖分析类型、原型个数和原型代表数据的精度,行汇总结果可以与使用所有数据得到的结果相媲美。 - 数据离散压缩
簇原型可以用于数据列压缩。例如,创建一个包含所有簇原型的表,即每个原型赋予-个整数值,作为它在表中的位置(索引)。 每个对象用于它所在的簇相关联的原型的索引表示。这类压缩称作
向量量化(vector quantization),并常常用于图像、声音和视频数据。
无论是用于数据降维还是离散压缩,都将损失-定的数据信息量,而能够使用聚类进行信息浓缩的
数据的特点是:
(1) 许多数据对象之间高度相似
(2) 某些信息丢失是可以接受的
(3) 希望大幅度压缩数据量 - 有效地发现最近邻
很多机器学习算法都是基于距离的模型,即找出最近邻可能需要计算所有点对点之间的距离,如之前介绍的KNN。通常我们可以使用簇原型减少发现对象最近邻所需要计算的距离的数目。直观地说,如果两个簇原型相距很远,则对应簇中的对象不可能互为近邻。这样,为了找出一个对象的最近邻,只需要计算到邻近簇中对象的距离,其中两个簇的邻近性用其原型之间的距离度量,从而大幅降低KNN类算法的计算量。
1.2 核心概念
在讨论具体的聚类技术之前,还需要讨论必要的背景知识。首先,我们就聚类分析中的核心概念展开讨论。
1.2.1 聚类分析
聚类分析仅根据在数据中发现的描述对象及其关系的信息,将数据对象分组。其目标是,组内的对象相互之间是相似的(相关的),而不同组中的对象是不同的(不相关的)。组内的相似性(同质性)越大,组间差别越大,聚类就越好。
1.2.2 簇
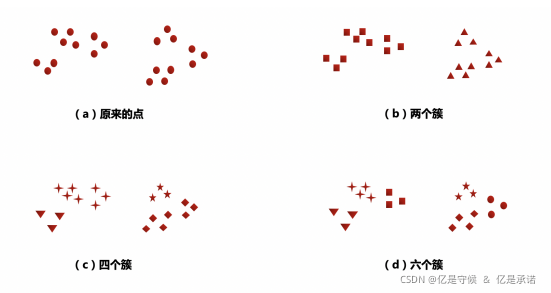
简单来说,簇就是分类结果的类,但实际上簇并没有明确的定义,并且簇的划分没有客观标准,我们可以利用下图来理解什么是簇。该图显示了20个点和将它们划分成簇的3种不同方法。标记的形状指示簇的隶属关系。下图分别将数据划分成两部分和六部分。然而,将2个较大的簇都划分成3个子簇可能是人的视觉系统造成的假象。此外,说这些点形成4个簇可能也不无道理。该图表明簇的定义是不精确的,而最好的定义依赖于数据的特性和期望的结果。聚类分析与其他将数据对象分组的技术相关。例如,聚类可以看作一种分类,它用类(簇) 标号创建对
象的标记。然而,只能从数据导出这些标号。相比之下,KN则是监督分类(supervisedclassfication),即使用由类标号已知的对象开发的模型,对新的、无标记的对象赋予类标号。为此,有时称聚类分析为非监督分类(unsupervised classification)。在数据挖掘中,不附加任何条件使用术语分类时,通常是指监督分类。
1.3 基于原型的聚类技术: K-Means
1.3.1 基于原型的簇
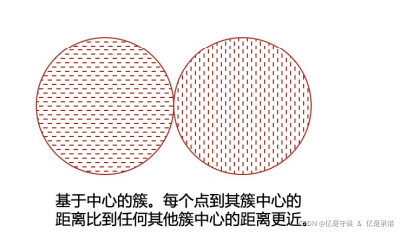
此时簇是对象的集合,并且其中每个对象到定义该簇的原型的距离比到其他簇的原型的距离更近(或更加相似)。 对于具有连续属性的数据,簇的原型通常是质心,即簇中所有点的平均值。当质心没有意义时(例如当数据具有分类属性时),原型通常是中心点,即簇中最有代表性的点。对于许多数据类型,原型可以视为最靠近中心的点;在这种情况下,通常把基于原型的簇看作基于中心的簇(center-basedcluster)。毫无疑问,这种簇趋向于呈球状。下图是一个基于中心簇的例子。
1.3.2. K-Means基本定义
K均值算法比较简单,我们从介绍它的基本算法开始。首先,选择K个初始质心,其中K是我们指定的参数,即所期望的簇的个数。每个点指派到最近的质心,而指派到一个质心的点集为一个簇。然后,根据指派到簇的点,更新每个簇的质心。重复指派和更新步骤,直到簇不发生变化,或等价地,直到质心不发生变化。
K-Means的核心任务就是根据我们设定好的K,找出K个最优的质心,并将离这些质心最近的数据分别分配到这些质心代表的簇中去。具体过程可以总结如下:

那什么情况下,质心的位置会不再变化呢?当我们找到一个质心,在每次迭代中被分配到这个质心上的样本都是一致的,即每次新生成的簇都是一致的,所有的样本点都不会再从一个簇转移到另一个簇,质心就不会变化了。这个过程在可以由下图来显示,我们规定,将数据分为4簇(K=4) ,其中白色X代表质心的位置:

在数据集下多次迭代(iteration),就会有:

可以看见,第六次迭代之后,基本上质心的位置就不再改变了,生成的簇也变得稳定。此时我们的聚类就完成了,我们可以明显看出,K-Means按照数据的分布, 将数据聚集成了我们规定的4类,接下来我们就可以按照我们的业务需求或者算法需求,对这四类数据进行不同的处理。
1.3.3 算法执行细节
聚类算法聚出的类有什么含义呢?这些类有什么样的性质?我们认为,被分在同一个簇中的数据是有相似性的,而不同簇中的数据是不同的,当聚类完毕之后,我们就要分别去研究每个簇中的样本都有什么样的性质,从而根据业务需求制定不同的商业或者科技策略。聚类算法的目的就是追求“簇内差异小,簇外差异大”。而这个“差异”,由样本点到其所在簇的质心的距离来衡量。
对于一个簇来说,所有样本点到质心的距离之和越小,我们就认为这个簇中的样本越相似,簇内差异就越小。而距离的衡量方法有多种,令x表示簇中的一个样本点,μ表示该簇中的质心,n表示每个样本点中的特征数目,表示组成点x的每个特征,则该样本点到质心的距离可以由以下距离来度量。
距离衡量方法
常见距离衡量方法即对应公式如下所示:
● 数据距离
对于数据之间的距离而言,在欧式空间中我们常常使用欧几里得距离,也就是我们常说的距离平方
和开平方,其基本计算公式如下:
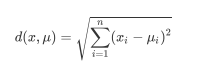
除此之外,还有曼哈顿距离,也被称作街道距离,该距离的计算方法相当于是欧式距离的1次方表示形式,其基本计算公式如下:
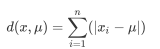
当然,不管是欧式距离还是曼哈顿距离,都可视为闵可夫斯基距离的-种特例,该距离计算公式如下:
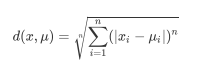
当n为1时,就是曼哈顿距离,当n为2时即为欧式距离,当n趋于无穷时,即为切比雪夫距离 。
文本距离
而除了数据距离之外,距离的衡量还常见于文本数据之间,此时我们常用余弦相似性或杰卡德相似度来进行衡量,余弦相似性计算本质上就是计算余弦夹角,其基本计算公式如下:
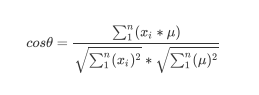
而杰卡德相似度则主要以集合运算为主:
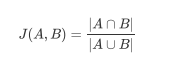
1.3.4 误差平方和SSE (Sum of the Squared Error, SSE)
此处引入机器学习算法中非常重要的概念,误差平方和,也被称为组内误差平方和。该概念在聚类和回归算法中均有广泛应用。在聚类算法中所谓误差平方和是指每个数据点的误差,即它到最近所属类别质心的欧几里得距离,然后求和汇总既得误差平方和。在聚类算法中,SSE是我们判断模型是否最优的重要指标,我们希望求得的模型是在给定K值得情况下SSE最小的模型,即在相同的K值情况下聚类模型SSE越小越好,这也是聚类算法最核心的优化条件。
1.3.5 聚类目标函数和质心计算方法
聚类算法中的目标函数是实现聚类这一目标所使用的函数,如最小化对象到其所属类的质心距离等,这里需要注意,-般如果采用距离作为邻近度衡量标准,则目标函数往往是利用最小距离来构建聚类类别,而若采用相似度作为邻近度衡量标准,则目标函数就是利用最大化相似度和来构建聚类类别。
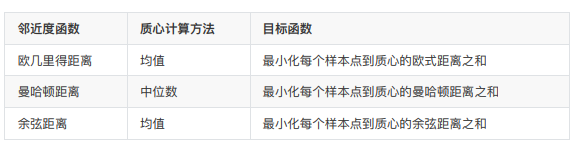
而质心是聚类类别的原型,-般可用均值或中位数来表示。但无论如何,在一旦确定距离衡量方法或邻近度函数(如欧式距离等),并 在模型优化条件(SSE最小) 的指导下,目标函数和质心选取方法都会随之确定,常用邻近度函数、质心和目标函数组合如下:
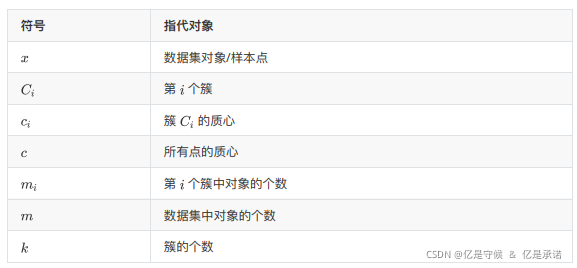
而这一切实际上是建立在严格的数学理论推导的基础之上的,推导方法之一就是利用EM算法进行计算。首先,我们需要定义聚类算法中的符号集:
然后,误差平方和可由下列计算公式表示:
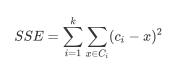
其中,C; 是第i个簇,x是C;中的点,C是第i个簇的质心。我们这里验证最常用的,当采用欧式距离时当且仅当质心为均值的时候才能够保证在目标函数的聚类过程中SSE保持最小。要保证在给定K值情况”下总SSE最小,则用梯度下降理论工具可将问题转化为为了保证总SSE最小,K的每一步取值,即K值每增加1,都要能够最大程度降低SSE,即在给定K值步长为1的情况下去找SSE下降速度最快的坡度(详见逻辑回归)。即簇的最小化SSE的最佳质心是簇中各点的均值。同样可类似证明采用曼哈顿距离时最佳质心选取方案是选取中位数,而当采用余弦夹角衡量相似度时,均值是最佳的质心计算方法。