- Unsupervised Learning–Linear Methods
- K-means
- dimension reduction
- Principle component analysis(主成分分析)(PCA)
- Non-negative matrix factorization(NMF)
- Locally Linear Embedding(LLE)
- Laplacian Eigenmaps(拉普拉斯自映射)
- T-distributed Stochastic Neighbor Embedding
二十二、Unsupervised Learning–Linear Methods
Dimension Reduction(降维)分为两种:
??Generation(无中生有);
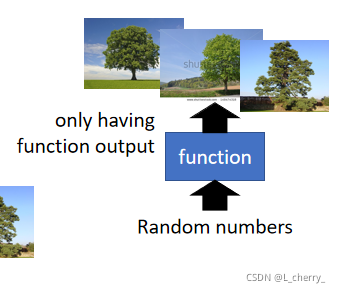
??Reduction(化繁为简):Clustering & Dimension
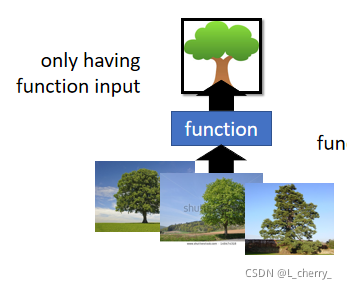
??
1、Clustering
??有一大堆的image,把它们分成一类一类的,然后把每一类贴标签分为cluster 1 ,cluster 2 等等:
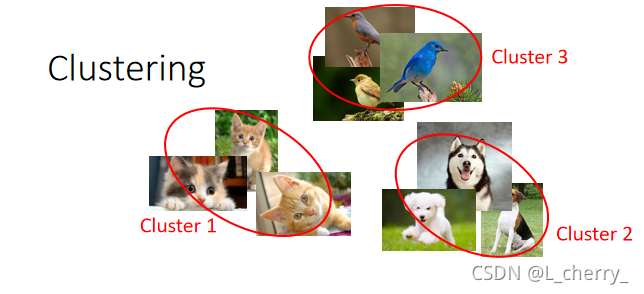
??现在的问题是到底要多少cluster?
??最常用的方法叫做K-means:
??(1)有一大堆unlabelled data
X
=
{
x
1
,
.
.
.
,
x
n
,
.
.
.
,
x
N
}
X =\begin{Bmatrix} x^1,...,x^n,...,x^N \end{Bmatrix}
X={x1,...,xn,...,xN?},每个
x
x
x都代表一张image,要把它们做成K个cluster;
??(2)首先找这些clutster的center,需要K个center,初始的center从training data中随机地找K个object,center
c
i
,
i
=
1
,
2
,
.
.
.
,
K
c^i , i = 1,2,...,K
ci,i=1,2,...,K,(K random
x
n
x^n
xn from
X
X
X);
??(3)repeat:
??for all
x
n
x^n
xn in
X
X
X:
????
b
i
n
{
1
x
n
i
s
m
o
s
t
"
c
l
o
s
e
"
t
o
c
i
0
O
t
h
e
r
w
i
s
e
b_i^n \left\{\begin{matrix} 1 \quad\quad x^n\quad is \quad most\quad "close"\quad to \quad c^i\\ 0 \quad\quad\quad \quad \quad \quad \quad \quad \quad \quad \quad Otherwise \end{matrix}\right.
bin?{1xnismost"close"toci0Otherwise?
??即决定现在的每一个object属于哪一个cluster,
b
i
n
b_i^n
bin?代表第n个object属于第i个cluster
??update你的cluster–update all
c
i
c^i
ci:
????
c
i
=
∑
x
n
b
i
n
x
n
/
∑
x
n
b
i
n
c^i = \sum_{x^n}^{}b_i^nx^n/ \sum_{x^n}^{}b_i^n
ci=∑xn?bin?xn/∑xn?bin?
??即把所有属于第i个cluster的object统统拿出来做平均,得到第i个cluster的center。
??
??clustering还有另一个方法叫做Hierarchical Agglomerative Clustering(HAC)(层次聚合聚类方法):
??(1)先建立一个tree,例如现在有5个example,想对它们建立tree structure,把这5个example两两去算它的相似度,然后挑最相似的一对;
??(2)pick a threshold(门槛),决定在哪个位置切开:
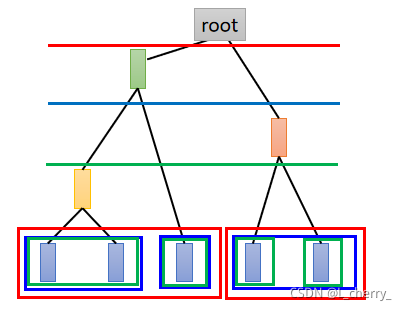
??
??但是只做cluster是比较卡的,因为每个cluster都比较以偏概全,所以应该用一个vector来表示object,这个vector中的每一个dimension就代表了某一种特质,这件事情就叫做distributed representation。
??如果原来的object是一个非常high dimension的东西,比如image,那么现在把它用它的特质来描述,它就会从比较高维的空间,变成比较低维的空间,这件事情就叫做Dimension Reduction(降维)。
??
2、Dimension Reduction
??举例:考虑MNIST,在MNIST中一个digit是一个28x28 dimension的图片来描述,实际上多数28x28的dimension的vector看起来都不像数字。
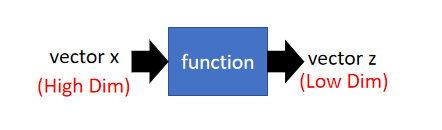
??那么怎么做Dimension Reduction?
??找一个function,这个function的input是一个vector
x
x
x,它的output是另外一个vector
z
z
z,并且
z
z
z的dimension比input
x
x
x小。
??最简单的方法就是 Feature selection(特征选择):
??在二维的平面上,发现data都集中在
x
2
x_2
x2?这个dimension,
x
1
x_1
x1?这个dimension没什么用就把它拿掉,选择
x
2
x_2
x2?:
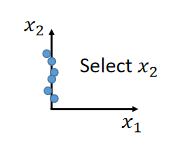
??这个方法不总是有用。
??
??另外一个常见的方法叫做Principle component analysis(主成分分析)(PCA):
??Dimension Reduction的function是一个很简单的linear function,input
x
x
x和output
z
z
z之间的关系就是一个linear的transform,根据一大堆的
x
x
x,在
z
z
z未知的情况下把
W
W
W找出来:
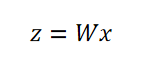
(细节参考 Bitshop第12章)
??PCA:
??找
W
W
W怎么找?假设现在考虑一个比较简单的case,即把我们的data降到一维的空间上,
z
z
z是一个一维的vector,我们把
x
x
x跟
W
W
W的第一个row
w
1
w^1
w1做inner product,我们就得到一个scalar。
??
w
1
w^1
w1长什么样子?首先假设
w
1
w^1
w1的长度(2-norm)是1:
∥
w
1
∥
2
=
2
\left \| w^1 \right \|_2 = 2
∥∥?w1∥∥?2?=2,意味着
w
w
w和
x
x
x是高维空间中的一个点,
w
1
w^1
w1是高维空间中的一个vector,所以
z
1
z_1
z1?就是
x
x
x在
w
1
w^1
w1上的投影:
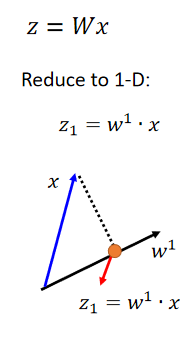
??所以现在做的事情就是把一堆
x
x
x,透过
w
1
w^1
w1把它投影变成
z
1
z^1
z1我们就得到一堆
z
1
z_1
z1?。不一样的
w
1
w^1
w1得到的结果也是不一样的:
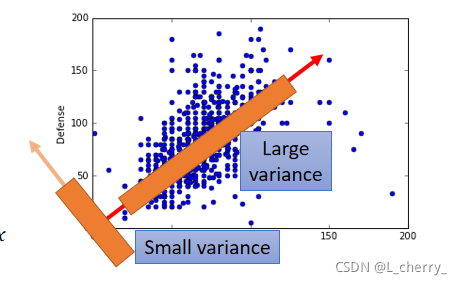
??要给一个目标才知道选什么样的
w
w
w,现在的目标是这样:我们希望选一个
w
1
w^1
w1,它通过projection得到
z
1
z_1
z1?的(variance)分布是越大越好。我们希望经过这个projection以后,不同的data point它们之间的区别仍然是看的见的。
??用公式表示:
??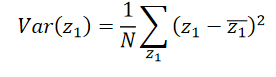
??假设想投影到2维的平面,就把
x
x
x跟另外一个
w
2
w^2
w2做inner product得到
z
2
z_2
z2?,找
z
2
z_2
z2?的公式和
z
1
z_1
z1?相同,但是这样的得到的结果也会相同,所以要在加一个constrain(约束):
w
1
w^1
w1和
w
2
w^2
w2得是垂直的,或者是
w
1
?
w
2
=
0
w^1 \cdot w^2 = 0
w1?w2=0。
??就用这个方法可以找出你想要的
w
w
w,数量由自己决定,最后再排在一起:

??
W
W
W是Orthogonal matrix(正交矩阵)。
??
??接下来的问题是怎么找
w
1
w^1
w1和
w
2
w^2
w2?
??拉格朗日乘子法:

??其中Cov代表covariance(协方差)。
??也就是说找
w
1
w^1
w1可以maximize
(
w
1
)
T
S
w
1
(w^1)^TSw^1
(w1)TSw1,constrain:
‖
w
1
‖
2
=
(
w
1
)
T
w
1
=
1
‖w^1‖_2=(w^1)^Tw^1=1
‖w1‖2?=(w1)Tw1=1。&w^1& is the eigenvector(特征向量) of the covariance matrix S,Corresponding(相应的) to the largest eigenvalue
λ
1
λ_1
λ1?,过程:

??
w
2
w^2
w2 is the eigenvector of the covariance matrix S,但是Corresponding to the 2nd largest eigenvalue
λ
2
λ_2
λ2?,求解
w
2
w^2
w2过程:

??
??
??PCA–decorrelation(去相关):
??
z
z
z的covariance会是一个Diagonal matrix(对角矩阵),也就是说如果做PCA,原来的data 的distribution可能是下图左的样子,做完PCA会做decorrelation,会让不同dimension之间的covariance是0:
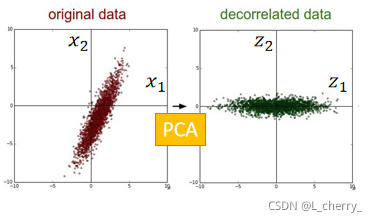
??也就是说如果算
z
z
z的covariance matrix的话会发现,它是Diagonal matrix,这样做的好处:假设现在PCA所得到的新的feature,这个新的feature是要给其它的model用的,假设是generative model,那用Gaussian来描述某一个class 的distribution,而你在做这个Gaussian的假设时你假设你的input data的covariance就是decorrelated,这样可以减少参数量,可以用比较简单的model来处理你的input data ,这样可以避免overfitting的情形。

??其中
e
1
e^1
e1就是第一维是1其它都是0的vector。
??
??PCA–Another Point of View:
??举例:考虑手写数字问题,这些数字是由一些basic component所组成的,这些basic component可能就是代表的笔画,写作
u
1
u^1
u1、
u
2
u^2
u2…把这些component加起来之后得到的vector就代表一个digit,或者把它们写成formulation:
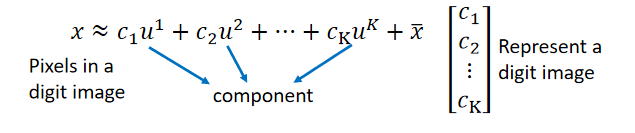
??比如说7是以下所有component加起来的结果,所以对7来说:
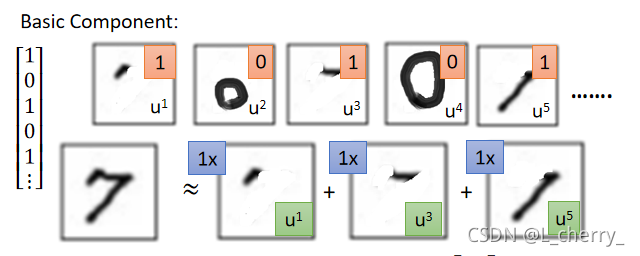
??把上式的
x
ˉ
\bar{x}
xˉ移到等号左边得到
x
^
\hat{x}
x^:
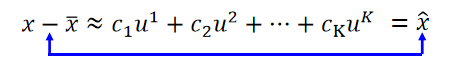
??现在假设我们不知道这些component
u
1
u^1
u1…是什么,怎么找这些呢?就是让
x
^
\hat{x}
x^和
x
?
x
ˉ
x-\bar{x}
x?xˉ越接近越好。它们中间的差就是Reconstruction error(重建误差):

??接下来要做的事情就是找
{
u
1
,
.
.
.
,
u
K
}
\begin{Bmatrix} u^1,...,u^K \end{Bmatrix}
{u1,...,uK?} minimize the error:
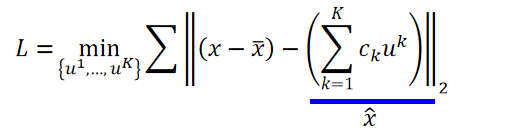
??

??简单来说:
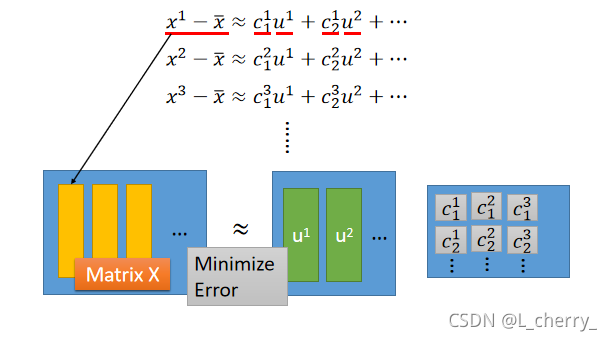
??怎么解上面的式子呢?
??用SVD(奇异值分解)的方法将Matrix X可以拆分成matrix U乘上matrix
Σ
\Sigma
Σ,乘上一个matrix V:
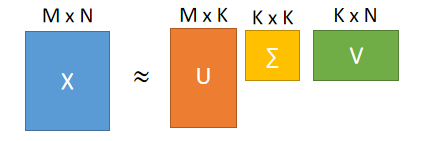
??U的K个column就是一组orthonormal eigen的vector ,它们是
X
X
T
XX^T
XXT的最大的k个eigenvalue。U的解就是PCA 。
??
??PCA跟neural network的关系:

??以上的事情可以想成用neural network来表示,假设我们的
x
?
x
ˉ
x-\bar{x}
x?xˉ是一个vector,这里写作一个3维的vector,假设K = 2,先算出
c
1
c_1
c1?和
c
2
c_2
c2?,就是把
x
?
x
ˉ
x-\bar{x}
x?xˉ的每一个component乘上
W
1
W^1
W1的每一个component,接下来你就得到
c
1
c_1
c1?:
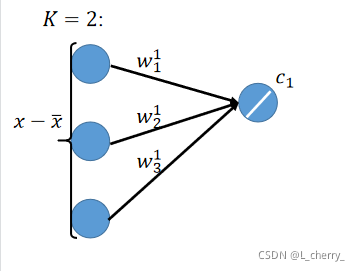
??然后把
c
1
c_1
c1?乘上
W
1
W^1
W1:
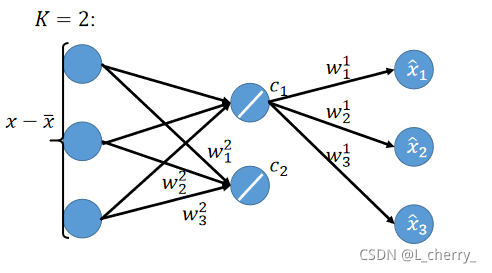
??同理得到
c
2
c_2
c2?,再乘上
W
2
W^2
W2与
c
1
c_1
c1?得到的结果相加得到
x
^
\hat{x}
x^。接下来minimize error,让
x
^
\hat{x}
x^跟
x
?
x
ˉ
x-\bar{x}
x?xˉ越接近越好。
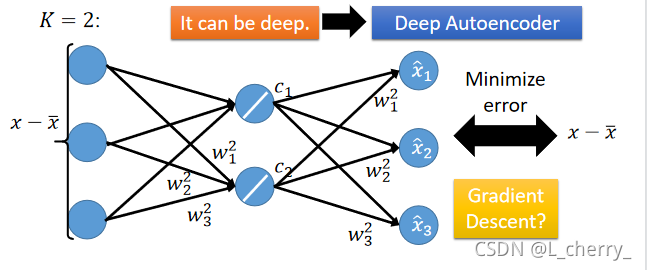
??PCA可以表示成只有一个hidden layer的neural network,这个hidden layer是linear activation function,我们train这个neural network是希望这个network的output和input越接近越好,这个叫做Autoencoder(自编码)。
??用neural network求出
W
W
W,跟用PCA得出的结果不一样。
??
??PCA的弱点:
??(1)PCA是unsupervised,假如给它一堆没有label的点,把它们project到一维上,PCA可以找一个可以让data varies最大的那个dimension。但是有一个可能是这两组data point它们分别代表了两个class,如果用PCA这个方法做dimension reduction的话就会使这两个class被merge在一起。这个可能需要引入label data,LDA就是考虑label data的一个降维方法(supervised)。
??(2)另外一个PCA的弱点就是它是linear的,期待做dimension reduction把下图S型的曲面拉直,这件事情对PCA来说是做不到的,得到的只能像下图一样被打扁。

??
??PCA的应用:(1)分析宝可梦的data;

(2)手写数字辨识MNIST;

??(2)人脸辨识;
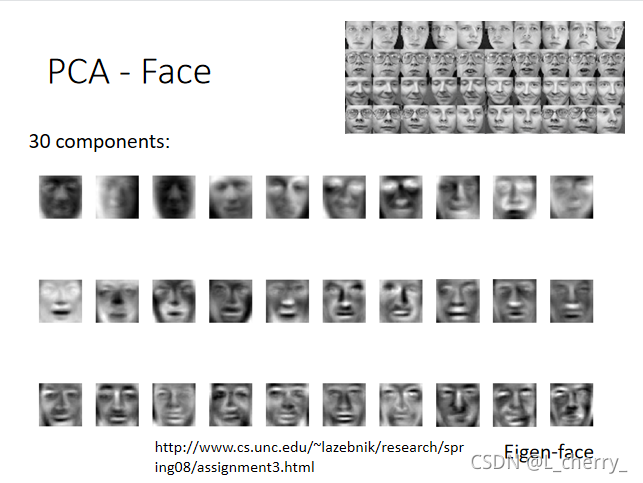
??
??PCA找出来的component不一定是一个图的part,如果你想要得到类似“笔画”的东西,可以使用另外的技术–Non-negative matrix factorization(NMF)(非负矩阵分解):
??PCA可以看做对matrix
x
x
x做SVD,但它分解出来的两个matrix的值可以是正的,可以是负的。现在如果用NMF,会强迫所有的component weight都是正的,是正的好处就是现在这张image必须由component叠加得到;所有component的dimension必须是正的,看起来更像是“笔画”。
??
??
二十三、Unsupervised Learning–Neighbor embedding
非线性降维:
??data point可能是在高维空间的里的manifold,地球的表面就是一个manifold,它是一个二维的平面被塞到一个三维的空间,在这个manifold里面只有很近距离的点Euclidean distance(欧氏距离)才会成立。
??manifold learning要做的事情就是把如下图S型的data point展开,把塞在高维空间里的低维空间摊平,摊平的好处是可以在这个摊平的平面上使用欧氏距离计算点和点之间的距离。
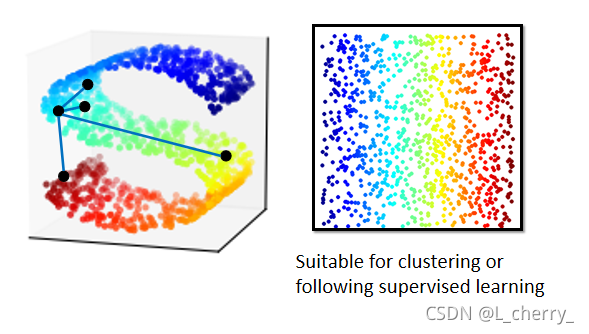
??类似的方法很多:
(一)Locally Linear Embedding(LLE)(局部线性嵌入)
??在原来的空间里,你的点的分布如下图,某一个点叫做
x
i
x^i
xi,选出
x
i
x^i
xi的neighbor
x
j
x^j
xj,接下来找
x
i
x^i
xi和
x
j
x^j
xj的关系,写作
w
i
,
j
w_{i,j}
wi,j?。
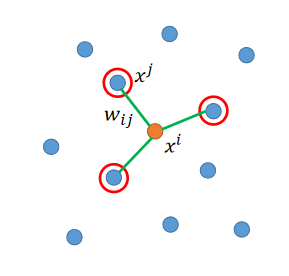
??这个
w
i
,
j
w_{i,j}
wi,j?怎么找出来呢?
??假设每一个
x
i
x^i
xi都可以用它的neighbor做linear combination以后组合而成,现在要找一组
w
i
,
j
w_{i,j}
wi,j?,这组
w
i
,
j
w_{i,j}
wi,j?对
x
i
x^i
xi的所有neighbor
x
j
x^j
xj做weighted sum时,它可以跟
x
i
x^i
xi越接近越好:
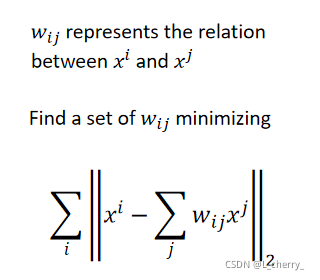
??接下来做dimension reduction,把原来所有的
x
i
x^i
xi和
x
j
x^j
xj转成
z
i
z^i
zi和
z
j
z^j
zj,并且它们之间的关系
w
i
,
j
w_{i,j}
wi,j?是不变的。
??
??LLE具体步骤:
??首先
w
i
,
j
w_{i,j}
wi,j?在原来的space上找完以后就定住,不变,接下来为每一个
x
i
x^i
xi和
x
j
x^j
xj找另外一个vector,做dimension reduction,我们要找
z
i
z^i
zi和
z
j
z^j
zj可以minimize下面这个function:

??这个LLE并没有明确的function告诉你怎么做dimension reduction。用LLE的好处:就算是原来的
x
i
x^i
xi和
x
j
x^j
xj不知道,只知道
w
i
,
j
w_{i,j}
wi,j?,也可以用LLE。
??LLE需要好好地调一下label的数目:
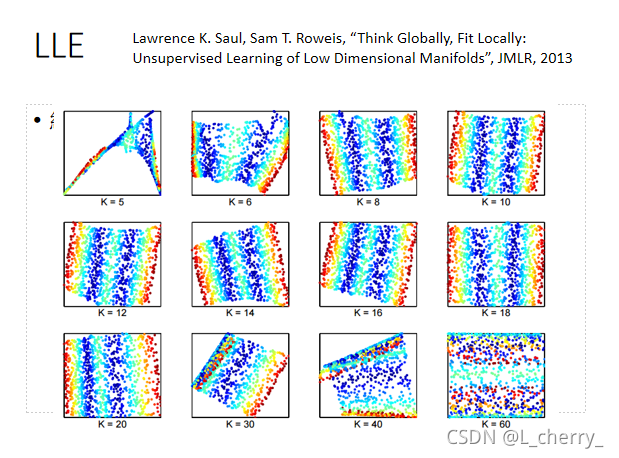
??
(二)Laplacian Eigenmaps(拉普拉斯自映射)
??把data point construct成一个graph,算data point两两之间的相似度,如果相似度超过一个值就把他们连接起来。
??在semi-supervised learning:如果
x
1
x^1
x1和
x
2
x^2
x2在high density region上是相近的,那么它们的label
y
^
1
\hat{y}^1
y^?1和
y
^
2
\hat{y}^2
y^?2很有可能是一样的。loss function有一项考虑有label data的项,另外一项是跟label data没有关系的可利用的unlabelled data,这项作用考虑我们得到的label是不是smooth的,作用很像regularization term。S表示得到的label有多么smooth:

??同样的道理可以应用在unsupervised 上面:Dimension Reduction–如果
x
1
x^1
x1和
x
2
x^2
x2在一个high density region上是接近的,那么我们也会希望
z
1
z^1
z1和
z
2
z^2
z2也是相近的。所以smooth的式子为:
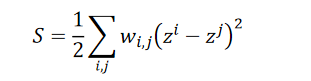
??找一个
z
i
z^i
zi和
z
j
z^j
zjminimize这个S的值,这样是有问题的吗?
??有问题,
z
i
z^i
zi和
z
j
z^j
zj设置成一样的值,并且都为0,那么
x
x
x就等于0,这个问题就结束了。
??所以要给
z
z
z一些constraint:如果今天
z
z
z降维后的空间为M,不希望你的
z
z
z分布在比M还要小的dimension,希望
S
p
a
n
{
z
1
,
z
2
,
.
.
.
,
z
N
}
=
R
M
Span\begin{Bmatrix} z^1,z^2,...,z^N \end{Bmatrix} = R^M
Span{z1,z2,...,zN?}=RM,Spectral clustering:clustering on
z
z
z。
??
(三)T-distributed Stochastic Neighbor Embedding(t-SNE)(T-分布随机邻域嵌入)
??前面的方法的问题:它们只假设相近的点应该是接近的,但没有假设不相近的点要分开。
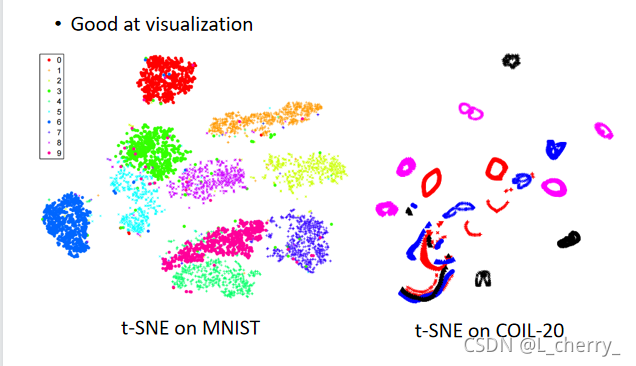
??比如LLE on MNIST:会遇到这样的情形–确实会把不同的class用不同的颜色表示,并且把同一个class的点聚集在一起,但是它没有防止不同class的点不要叠成一团,这些点还是挤在一起;
??比如LLE on COIL-20,每张图旋转的时候很像,但是正面和侧面是非常不一样的,下图的圈圈就显示你把某张图做旋转后再做dimension reduction所得到的结果。但是不同的object是挤成一团的。
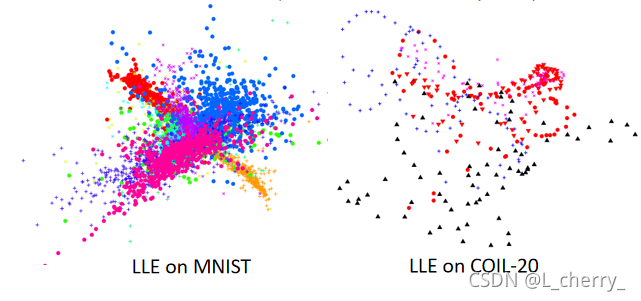
??t-SNE的做法:把原来data point
x
x
x变成low-dimension vector
z
z
z,在原来的
x
x
x这个space上我们会计算所有的点的pair
x
i
x^i
xi、
x
j
x^j
xj的similarity:
S
(
x
i
,
x
j
)
S(x^i,x^j)
S(xi,xj),接下来会做一个normalization,会计算一个
P
(
x
j
∣
x
i
)
P(x^j|x^i)
P(xj∣xi)(会计算所有data point之间的similarity):
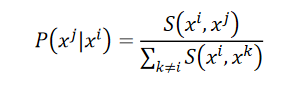
??假设已经找出了low-dimension的representation
z
z
z:
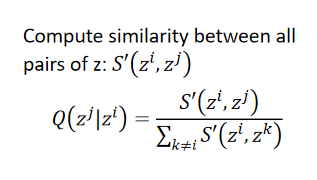
??接下来希望找一组
z
i
z^i
zi和
z
j
z^j
zj可以让以上两个distribution越接近越好,怎么衡量两个distribution之间的相似度?–KL散度:
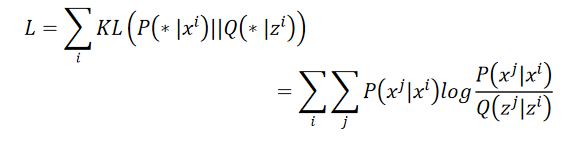
??因为做t-SNE时会计算所有data point之间的similarity,计算量很大,第一个常见的做法是先做降维。
??
??t-SNE 的Similarity Measure
??我们在原来的data point上,Similarity Measure选择以下的function:
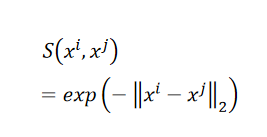
??在t-SNE之前的方法SNE的做法:
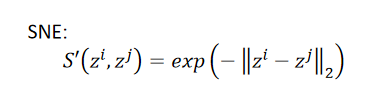
??t-SNE的做法:
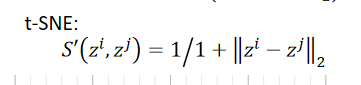
??对比图:

??t-SNE会把data point聚集成一群一群的:
??
??
??
本文是对blibli上李宏毅机器学习2020的总结,如有侵权会立马删除。