[人工智能]《FULLSUBNET: A FULL-BAND AND SUB-BAND FUSION MODEL FOR REAL-TIME SINGLE-CHANNEL SPEECH ENHANCEMENT》

abstract

本文提出了一个全频带和子频带混合的模型，名为：FullSubNet，用于单通道实时信号语音增强。全频带以及子频带指模型输入为全频带以及子频带的噪声频域特征，输出全频带以及子频带的语音目标。子频带模型（sub-band model）单独处理每一个频率。它的输入包括一个频率以及多个内容频率。输出为对相关频率的去噪（clean）语音目标。这两种模型具有不同的属性。全频带模型（full-band model）可以捕捉全局频域内容以及长程跨带（cross-band）依赖（dependency）。然而它缺失了能力去建模信号平稳性以及加入局部频域模式。sub-band model恰好相反。我们依次连接了pure full-band model以及pure sub-band model，并且使用了切实的联合的训练来聚合这两种模型的优点。我们在DNS挑战数据集上进行了实验来验证提出的模型。实验结果显示full-band和sub-band信息是互补的，以及FullSubNet可以有效地聚合它们。FullSubNet的表现超过了DNS挑战中的top-ranked methods。

1.introduction

近年来，基于深度学习的单通道信号增强方法大大提升了语音增强系统的语音质量和可理解性。这些方法通常是有监督的并且可以被划分为时域和频域方法。时域方法使用神经网络将噪声信号波映射为clean信号波。而频域方法使用噪声频域特征（如：复杂波谱、量级波谱）作为神经模型的输入。学习目标是clean speech或者一个特定的mask of频域特征。通常地，由于时域信号的高维以及显式几何结构的缺失，频域信号方法仍然为语音增强方法的主流。在本文，我们关注于频域中的实时单通道信号增强。

一种我们之前提出的sub-band-based method：(1)它学习频率信号稳态来辨别语音和稳态噪声。(2)它关注于存在于当前和内容频域中的局部频域模式。局部频域模式被证明是信息丰富的用于辨别语音和其他信号。
这种sub-band model满足了DNS挑战的实时性要求，表现也不错。但是它不能建模全局频域模式并且利用长程跨频依赖。特别地，对于具有特别低信噪比(SNR)的sub-band，sub-band模型很难恢复clean speech，即使它辅助了full-band dependency。另一方面，full-band model学习了高纬输入和输出之间的回归，缺失了机制处理sub-band information，如信号平稳性。

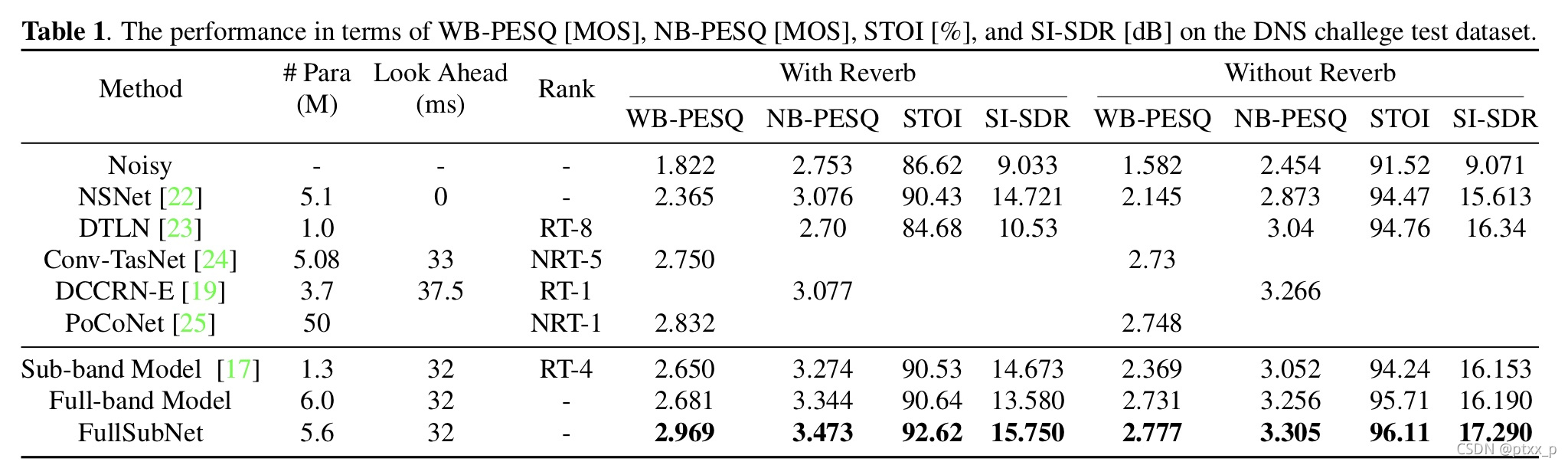
本文提出了一个full-band和sub-band融合模型：FullSubNet来解决上述问题。基于很多之前的实验，FullSubNet被设计为full-band模型和sub-band 模型的一系列联系。简而言之，full-band模型的输出是sub-band模型的输入。通过有效的joint训练，这两种模型被同时优化。FullSubNet可以同时捕捉全局（full-band）内容以及保持能力来建模信号稳定性以及添加局部频域模式。就像sub-band 模型，FullSubNet仍然满足了实时性要求以及可以利用在合理延迟下的未来信息。

2.method

我们使用了语音信号在短时傅立叶变换（STFT,short-time Fourier transform）下的表征:

本文只关注于去噪任务，目标是去除噪声$N(t,f)$，以及还原混响语音信号$S(t,f)$。我们提出了一个full-band和sub-band 混合模型来完成这个任务，包括一个pure full-band model $G_{full}$以及一个pure sub-band model $G_{sub}$。下图展示了基础工作流。

2.1. input

之前的工作已经证明了幅度谱特征（magnitude spectral feature）可以提供关于在full-band上全局频域模式的重要线索以及在sub-band上的局部频域模式及信号稳定性。因此，我们使用noisy full-band magnitude spectral features:

sub-band model $G_{sub}$根据信号稳定性以及在noisy sub-band signal中编码的局部频域模式以及full-band 模型的输出来预测frequency-wise clean-speech目标。具体来说，我们使用一个time-frequency 点$|X(t,f)|$以及它的邻接的$2\times N$ time-frequency points作为一个sub-band 单元。$N$是在每边考虑的邻居频率数目。对于边缘频率，$f?N<0或者f+N>F?1$,圆傅里叶频率被使用。我们拼接了sub-band unit以及full-band model的输出:$G_{full}(|X(t,f)|)$，作为sub-band model $G_{sub}$的输入。

因为full-band 频域特征$X(t)$包括F特征，我们最终生成F个维度为$2N+2$的独立的输入序列给$G_{sub}$。

2.2. learning target

毫无疑问，精确的相位估计可以提供更多的听觉感知质量改善，尤其是在
低信噪比 (SNR) 条件下。但是落在$?\pi ～\pi$的相位具有复杂的数据分布，使得相位估计变得困难。于是我们不对相位进行准确估计而是将complex idel ratio mask (cIRM)作为我们模型的学习目标。我们使用
双曲正切在训练中压缩 cIRM 并且在推理过程中对未压缩的mask使用逆函数（K = 10，C = 0.1）。我们对cIRM的一个T-F bin定义为$y(t,f)\in {\mathbb{R}}^2$。sub-band model将for f的序列$\tilde{x}(f)$作为输入，之后预测cIRM序列：

2.3 model architecture

在FullSubNet中的full-band和sub-band模型具有相同的模型架构，包括两个堆叠的无向LSTM层以及一层FC。full-band model的LSTM包括512隐藏单元，ReLU为激活函数。full-band模型在每个时间步上输出一个F维的向量，每个频率一个向量。sub-band unit和每个频域进行拼接来形成F个独立的输入样本（见公式4）。经过之前的实验，sub-band model不需要和full-band model一样大，因此在LSTM的每一层中就采用了384个隐藏单元，sub-band model的输出没有采用激活函数。需要说明的是，所有的频率共享一个sub-band network（以及它的参数）。在训练过程中，考虑限制的LSTM内存容量，输入-目标序列对通过一个固定长度的sequence生成。

为了使得模型更加容易被优化，输入序列必须和输入等级相等。对于full-band 模型，我们实验地计算了在full-band序列$\tilde{X}$上的振幅频域特征均值${\mu }_{full}$并且归一化了输入序列$\frac{\tilde{x}}{{\mu }_{full}}$。sub-band模型独立地处理这些频率。对于频率$f$,我们计算输入序列$\tilde{x}(f)$的均值${\mu }_{sub}(f)$并且归一化输入序列$\frac{\tilde{x}(f)}{{\mu }_{sub}(f)}$。

在实时的推理过程中，我们通常使用累计归一化方法，也就是说，用于归一化的均值使用所有的frames进行计算。然而，在实际的实时语音增强系统中，最开始的语音信号往往invalid。在本次工作中，为了更好地展示FullSubNet的表现而忽略归一化问题，我们直接使用在整个test clip上计算得到的${\mu }_{full}$和${\mu }_{sub}(f)$来在推理过程中使用归一化。

我们的方法支持输出延迟，使得模型可以在合理的小时延下探索未来信息。为了推理$y(t?\tau )$，未来的time step ,也就是说$x(t?\tau +1),...,x(t)$作为输入序列（就像图1中所示）。

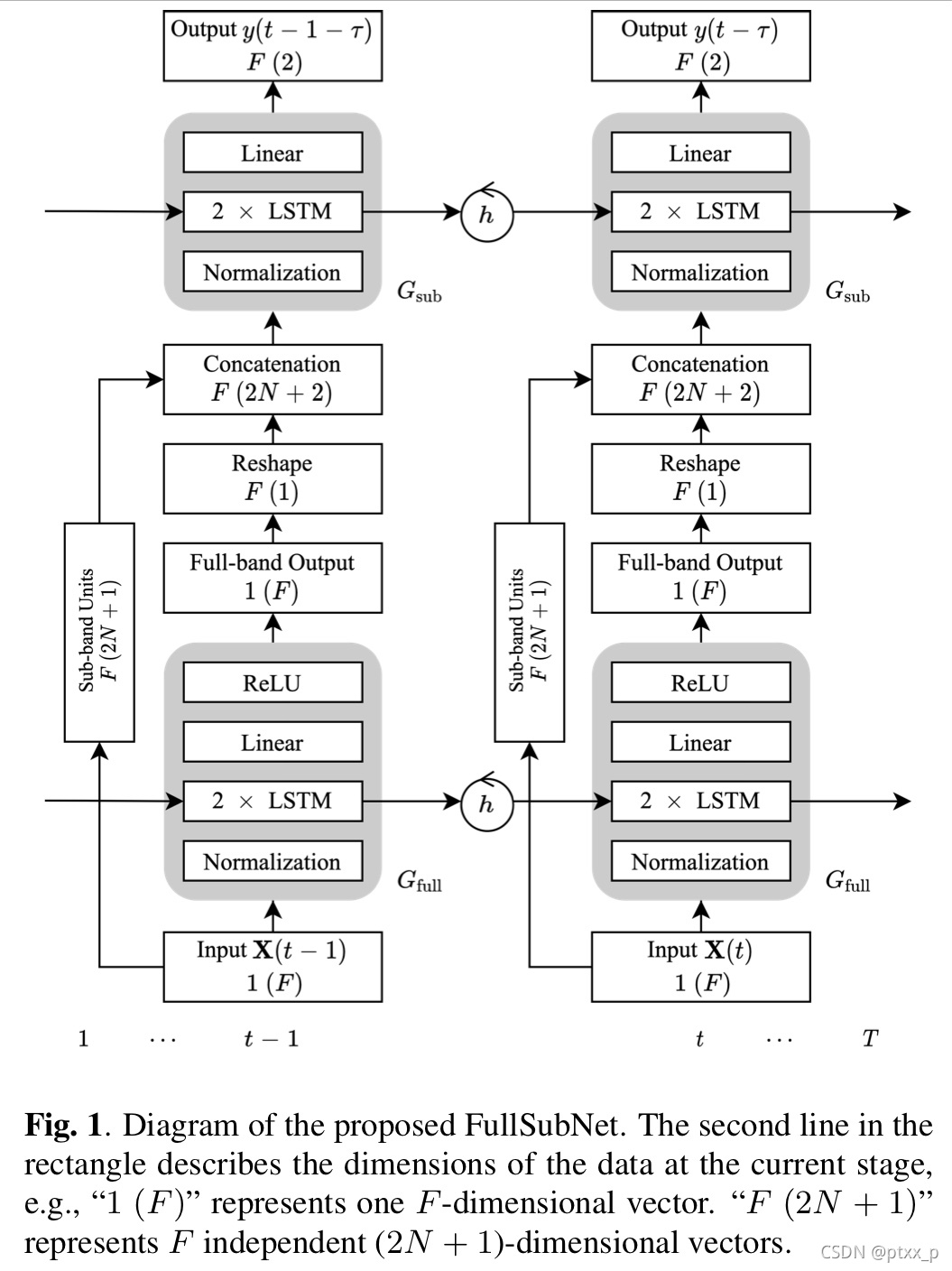
4.experimental result

full band模型的表现普遍优于sub-band model，因为full-band模型使用更大的网络来利用宽频信息。很有趣的现象是：sub-band model在“with reverb”数据上更加有效，full-band model则相反。这表明了sub-band model通过关注在narrow-band 频带上的时间演化有效地建模了回响效果。