5/1-3 BP神经网络的改进及MATLAB实现(下)
1. 自适应梯度下降法(Adagrad )
\qquad
我们知道,在更新权重与偏置时设置了学习率
η
\eta
η控制下降速度详见5/1-1 神经网络识别手写数字及MATLAB程序。
W
k
=
W
k
?
1
?
η
?
C
?
W
k
?
1
W^{k}=W^{k-1}-\eta\frac{\partial C}{\partial W^{k-1}}
Wk=Wk?1?η?Wk?1?C?
b
k
=
b
k
?
1
?
η
?
C
?
b
k
?
1
b^{k}=b^{k-1}-\eta\frac{\partial C}{\partial b^{k-1}}
bk=bk?1?η?bk?1?C?其中C为损失函数。若学习率设置过小,则权重与偏置更新缓慢,若学习率设置过大则容易越过最小值点(我们的目标是最小化损失函数),导致一直不能求得最小值点。所以学习率的选择非常关键。
\qquad
以开口向上的抛物线为例,我们希望越靠近最小值点学习率越小;梯度越大学习率越大,梯度越小学习率越小,于是我们可以用如下方法改进:
η
w
=
η
∑
i
=
1
t
(
?
C
?
W
i
)
2
+
?
\eta_w=\frac{\eta}{\sqrt{\sum_{i=1}^t(\frac{\partial C}{\partial W^{i}})^2+\epsilon}}
ηw?=∑i=1t?(?Wi?C?)2+??η?
上式表明,随着更新次数的变大,学习率越来越小。当
?
C
?
W
i
\frac{\partial C}{\partial W^{i}}
?Wi?C?趋于0时
η
w
\eta_w
ηw?趋于一个常数。此时
W
k
=
W
k
?
1
?
η
w
?
C
?
W
k
?
1
W^{k}=W^{k-1}-\eta_w\frac{\partial C}{\partial W^{k-1}}
Wk=Wk?1?ηw??Wk?1?C?
b
k
=
b
k
?
1
?
η
w
?
C
?
b
k
?
1
b^{k}=b^{k-1}-\eta_w\frac{\partial C}{\partial b^{k-1}}
bk=bk?1?ηw??bk?1?C?
2.动量法(momentum)
\qquad
当前步的下降方向,不只是由当前的梯度决定,而是由当前梯度与以往梯度共同决定。这样有可能跳出局部极小值,例如下图
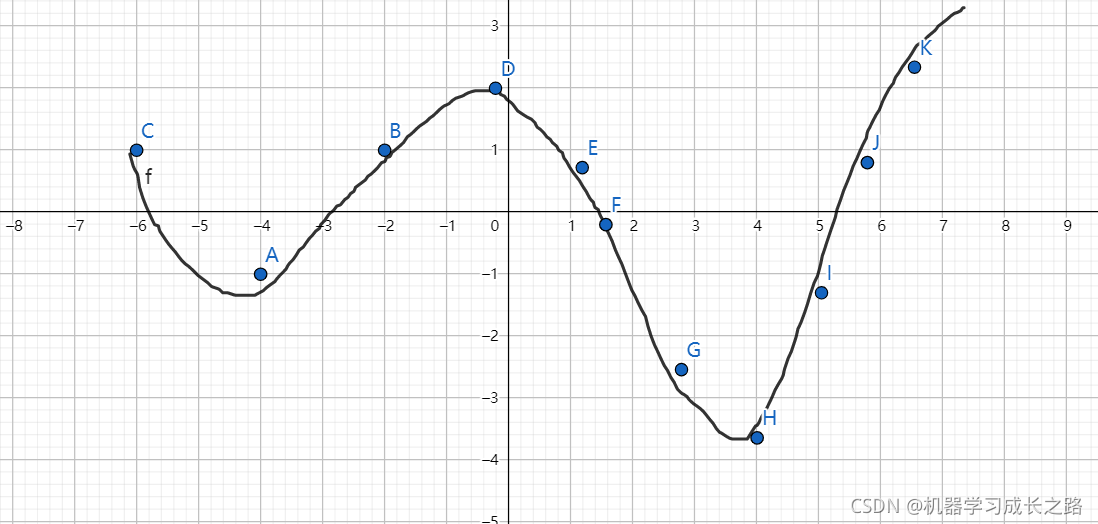
从C点出发,A点是局部极小值点,如果点走到B点,此时梯度与历史梯度反向,故更新方向会往A点走,很容易陷入局部极小。若改用动量法,以上一刻的梯度与此刻梯度的加权平均决定总梯度的方向(如上图,虽然在B点梯度与C点梯度相反,但若想达到全局最小,需要向C同负梯度方向更新)。故可用$
V
t
=
β
V
t
?
1
+
(
1
?
β
)
?
C
?
W
t
V^t=\beta V^{t-1}+(1-\beta)\frac{\partial C}{\partial W^{t}}
Vt=βVt?1+(1?β)?Wt?C?
W
t
=
W
t
?
1
?
η
V
t
W^t=W^{t-1}-\eta V^t
Wt=Wt?1?ηVt这里
β
\beta
β一般取
0.9
0.9
0.9。