1 复习感知机
??????? 复习下前一节的感知机,先来看看公式:
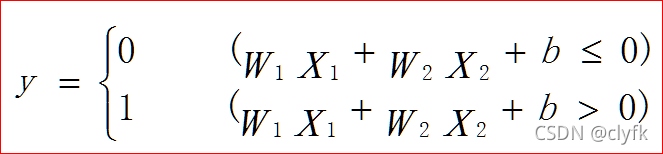
?
???????? 如果稍微把式子从另外一个角度来描述呢:
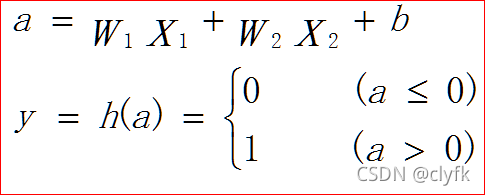
???????? 激活函数已经显露出来了,h()即是。如果把a作为一个神经元,权重W有了,输入X有了,偏置b有了,a输出到y就得有激活函数来转换,这个激活函数就是阶跃函数:
# coding: utf-8
import numpy as np
import matplotlib.pylab as plt
def step_function(x):
return np.array(x > 0, dtype=int)
X = np.arange(-5.0, 5.0, 0.1)
Y = step_function(X)
plt.plot(X, Y)
plt.ylim(-0.1, 1.1)
plt.show()
???????? 这里说个不是那么严格的定义,朴素感知机即是使用了阶跃激活函数的单层网络,多层感知机就可以说是神经网络了,一般都是使用了比阶跃函数更为平滑的激活函数的多层网络。神经元的多层连接的构造、信号的传递方法等,基本上和感知机是一样的。
?2 平滑的激活函数
??????? 阶跃激活函数上图已经很明了了,这节就看看sigmoid函数和relu函数,这里明确一点,这些激活函数都是非线性函数,神经元的多层连接正是因为非线性函数才能发挥多层网络带来的优势。如果使用线性函数,不管网络有多少层,都是可以使用单层网络描述的。
??????? 都是非线性函数,后两者相对更为平滑,但是宏观上三个函数的形状也是相似的,直接看图:
??????? sigmoid函数:
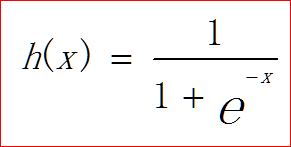
# coding: utf-8
import numpy as np
import matplotlib.pylab as plt
def sigmoid(x):
return 1 / (1 + np.exp(-x))
X = np.arange(-5.0, 5.0, 0.1)
Y = sigmoid(X)
plt.plot(X, Y)
plt.ylim(-0.1, 1.1)
plt.show()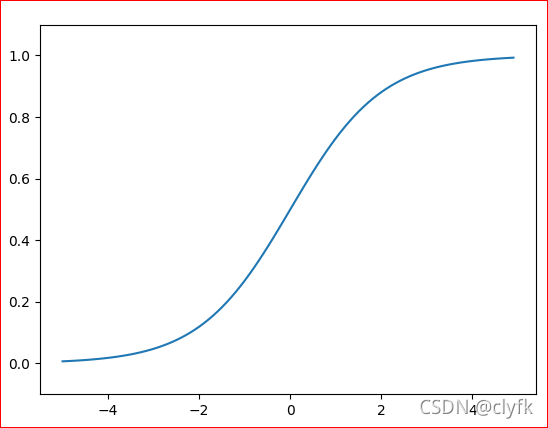
? ????? sigmoid和step函数,宏观上函数的形状也是相似的:
# coding: utf-8
import numpy as np
import matplotlib.pylab as plt
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def step_function(x):
return np.array(x > 0, dtype=np.int)
x = np.arange(-5.0, 5.0, 0.1)
y1 = sigmoid(x)
y2 = step_function(x)
plt.plot(x, y1)
plt.plot(x, y2, 'k--')
plt.ylim(-0.1, 1.1)
plt.show()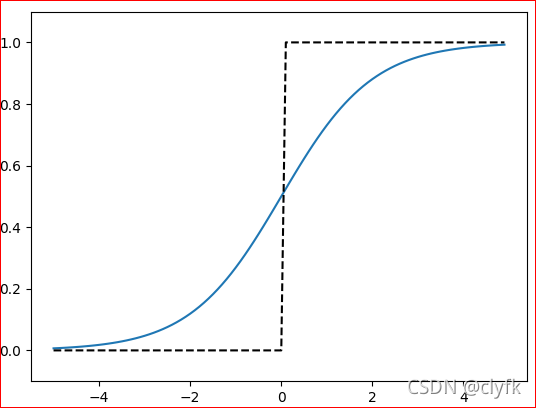
????????
relu函数:
 ?
?
# coding: utf-8
import numpy as np
import matplotlib.pylab as plt
def relu(x):
return np.maximum(0, x)
def step_function(x):
return np.array(x > 0, dtype=np.int)
x = np.arange(-5.0, 5.0, 0.1)
y = relu(x)
y0 = step_function(x)
plt.plot(x, y)
plt.plot(x, y0, 'k--')
plt.ylim(-0.1, 1.5)
plt.show()
? ? ? ?? 为了解决神经网络多层传递过程中趋于零的问题,平滑的激活函数使用得较为广泛,且为了算得更快,relu优势较为明显,看他们的公式就可知。relu也有好多的变体,都是在神经网络发展过程中遇到问题而做的改进。