[人工智能]机器学习-第九章 聚类

机器学习-第九章 聚类

D系鼎溜已关注

2020.02.19 10:36:17字数 3,312阅读 375

9.1 聚类任务

在无监督学习任务中，包括了密度估计、异常检测以及聚类等。其中应用最广泛的是聚类。

聚类就是对大量未知标注的数据集，按照数据的内在相似性将数据集划分为多个簇，使簇内的数据相似度高，两簇间的数据相似度低。

聚类试图将数据集中的样本划分为若干个通常是不相交的子集，每个子集称为一个"簇"。 通过这样的划分，每个簇可能对应于一些潜在的概念(类别) ，如"浅色瓜" "深色瓜"，"有籽瓜" "无籽瓜"等；注意，这些概念对聚类算法而言事先是未知的，聚类过程仅能自动形成簇结构，簇所对应的概念语义需由使用者来把握和命名。

更加具体来说，假设数据集D={x1,x2,……,xm}有m个样本；每个样本xi有n个属性特征，xi={xi1,xi2,……,xin}；则聚类算法将数据集D划分为k个不相交的簇，{Cl|l = 1,2,3,……,k}；用λj表示样本xj的"簇标记"，λj∈{1,2,……,k}，xj∈Cλj；聚类结果包含m个元素的簇标记向量λ=(λ1,λ2,……,λm)。

我们先讨论聚类算法涉及的性能度量和距离计算，再介绍几种不同类型的代表性聚类算法。

9.2 性能度量

要想获得好的聚类结果，我们希望聚类结果的"簇内相似度"高，而"簇间相似度"低，即同一簇的样本尽可能彼此相似，不同簇的样本尽可能不同。

聚类性能度量大致有两类。
一类是将聚类结果与某个"参考模型"进行比较，称为"外部指标"；
一类是直接考察聚类结果而不利用任何参考模型，称为"内部指标"。

• 外部指标

  

  

  根据上面四式，有常用的聚类性能度量外部指标

  

  上面三个性能度量的结果值均在[0,1]之间，且越大聚类结果越好。

• 内部指标
  设dist (·,·)用于计算两个样本之间的距离，μ代表簇C的中心点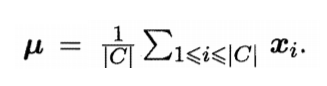

  

  

  

  

  

  

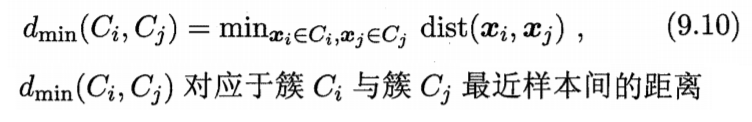
  基于式(9.8)-(9.11) 可导出下面这些常用的聚类性能度量内部指标: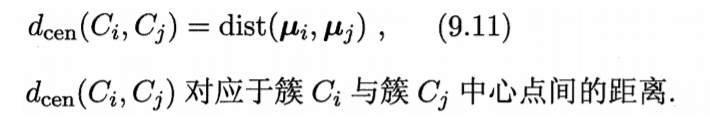

  

  
  其中，DBI的值越小聚类结果越好；而DI的值越大聚类结果越好。

9.3 距离计算

对于函数dist(·,·)，它是一个距离度量，其需要满足的基本性质：
1）非负性：dist(xi,xj)≥0
2）同一性：dist(xi,xj)=0当且仅当xi=xj
3）对称性：dist(xi,xj)=dist(xj,xi)
4）直递性：dist(xi,xj)≤dist(xi,xk)+dist(xk,xj)

样本属性还可以分为"无序属性"和"有序属性"
无序属性:如 {蜷缩,稍蜷,硬直}，{火车,飞机,轮船}
有序属性:如 {1,2,3}，{高,中,低}，{大,中,小}

• 对于有序属性的距离计算
  最常用的是闵可夫斯基距离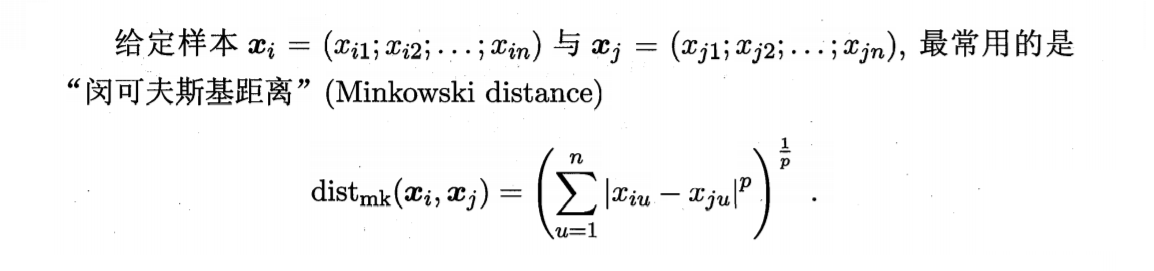

  

  
  当p=1时，闵可夫斯基距离为曼哈顿距离

  

  
  当p=2时，闵可夫斯基距离为欧氏距离

  

• 对于无序属性的距离计算

  对无序属性，采用VDM。

  

于是，将闵可夫斯基距离和VDM结合之后，可以处理混合属性。
假定有nc个有序属性、n-nc个无序属性，让有序属性排列在无序属性面前。有

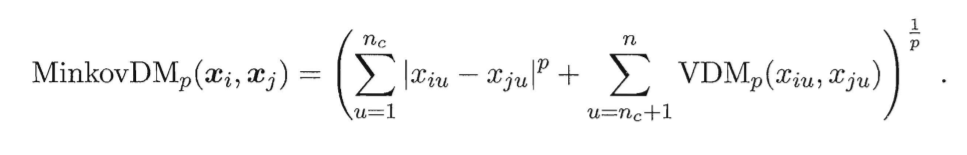
9.4 原型聚类

"原型"指：样本空间中具有代表性的点。
原型聚类亦称"基于原型的聚类"。
以下是几种知名的原型聚类算法。

1. k均值算法

基本思路：通过人工指定k的值确定分类簇的类别数，随机选择k个数据点作为各个簇的中心点，然后通过迭代将一类数据（相似度高的一类数据）划入各个簇中。

优点：易于实现、计算效率高。
缺点：需要事前指定簇的数量k，如果k值选择不当，则导致聚类效果不佳或产生收敛速度慢等问题。

给定样本集D={x1,x2,……,xm}，"k均值"算法针对聚类所得簇C={C1,C2,……,Ck}最小化平方误差

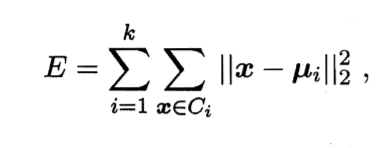
其中μi是簇Ci的均值向量

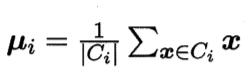
E越小，簇内样本相似度越高。

步骤：

• 从样本点中随机选取k个点作为初始簇中心；
• 将每个样本点划分到距离它最近到中心点所代表的簇中；
• 用各簇中所有样本的中心点替代原有的中心点；
• 重复步骤2和3，直到中心点不变或者达到预定迭代次数，算法终止。

具体流程：

举例：
给定数据集

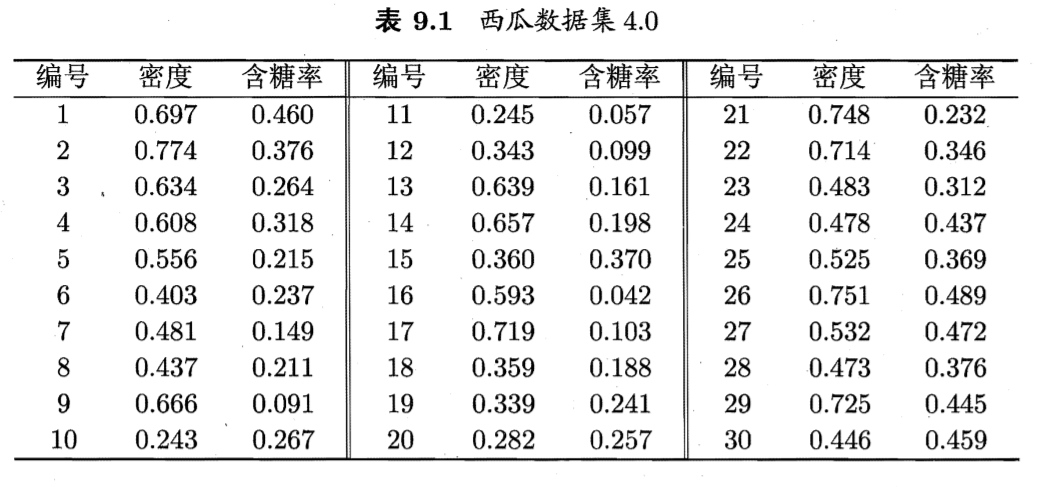
假定聚类簇数k=3，一开始随机取3个样本x6,x12,x27作为初始均指向量，即

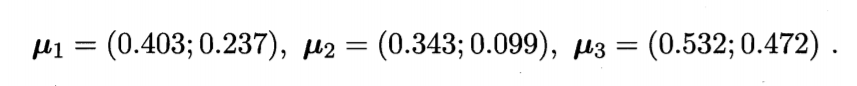
考察样本x1=(0.403;0.237)，它与μ1,μ2,μ3的距离分别为0.369,0.506,0.166，与μ3距离最短，因此x1划入簇C3中。类似的对数据集的样本考察一遍之后，可得到当前簇划分为

代码实现

import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
import seaborn as sns
import tensorflow as tf
#随机生成数据，2000个点，随机分为两类
num_puntos=2000
conjunto_puntos=[]#数据存放在列表中
for i in range(num_puntos):
    if np.random.random()<0.5:
        conjunto_puntos.append([np.random.normal(0.0,0.9),np.random.normal(0.0,0.9)])
    else:
        conjunto_puntos.append([np.random.normal(3.0,0.5),np.random.normal(3.0,0.5)])
 
df=pd.DataFrame({'x':[v[0] for v in conjunto_puntos],
                 'y':[v[1] for v in conjunto_puntos]})
sns.lmplot('x','y',data=df,fit_reg=False,size=6)
plt.show()
#lmplot, 首先要明确的是:它的输入数据必须是一个Pandas的'DataFrame Like' 对象,
#然后从这个DataFrame中挑选一些参数进入绘图充当不同的身份.
 
#把数组装进tensor中
vectors=tf.constant(conjunto_puntos)
k=4
#tf.random_shuffle（value,seed=None,name=None）：对value（是一个tensor）的第一维进行随机化。相当于把数据随机化
centroides=tf.Variable(tf.slice(tf.random_shuffle(vectors),[0,0],[k,-1]))
#随机选取K个点作为质心
 
#增加维度
expanded_vectors=tf.expand_dims(vectors,0)
expanded_centroides=tf.expand_dims(centroides,1)
 
diff=tf.sub(expanded_vectors,expanded_centroides)
sqr=tf.square(diff)
distance=tf.reduce_sum(sqr,2)
 
#挑选每一个点里的最近的质心（返回的是最小值索引）
assignments=tf.argmin(distance,0)
 
#tf.where（）返回bool型tensor中为True的位置，
#tf.gather(params, indices, validate_indices=None, name=None)合并索引indices所指示params中的切片
means=tf.concat(0,[tf.reduce_mean(tf.gather(vectors,
                                            tf.reshape(tf.where(tf.equal(assignments,c)),[1,-1])),
                                  reduction_indices=[1])for c in range(k)])
#tf.assign()用means更新centroides
update_centroides=tf.assign(centroides,means)
 
 
init=tf.global_variables_initializer()
sess=tf.Session()
sess.run(init)
 
for step in range(100):
    _,centroid_values,assignment_values=sess.run([update_centroides,centroides,assignments])
data={'x':[],'y':[],'cluster':[]}
 
for i in range(len(assignment_values)):
    data['x'].append(conjunto_puntos[i][0])
    data['y'].append(conjunto_puntos[i][1])
    data['cluster'].append(assignment_values[i])
df=pd.DataFrame(data)   
sns.lmplot('x','y',data=df,fit_reg=False,size=6,hue='cluster',legend=False)
#hue通过指定一个分组变量, 将原来的y~x关系划分成若干个分组;fit_reg：是否显示回归曲线
plt.show()

代码链接：https://blog.csdn.net/weixin_31866177/article/details/88246939

2. 学习向量量化(LVQ)

LVQ假设数据样本带有类别标记，学习过程中需要利用样本的标记来辅助聚类。

给定数据集D={(x1,y1),(x2,y2),……,(xm,ym)}，每个样本xj是有n个属性描述的特征向量(xj1,xj2,……,xjn)，yj∈Y是样本xj的类别标记。
LVQ的目的是学得一组n维原型向量{p1,p2,……,pq}，每个原型向量代表一个簇，簇标记为ti∈Y。LVQ算法如下

LVQ关键在于如何更新原型向量，即第6-10行。
对于样本xj，在第5行中得到与其最近的原型向量pi*之后；

• 若pi*与xj的标记相同，即yj与ti相同的话，则令pi*想xj的方向靠拢，此时新原型向量p'和新原型向量与xj的距离分别为

  

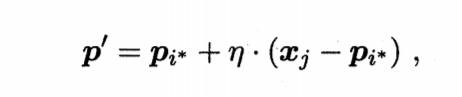
  新原型向量p'

  

  其中，η是学习率∈(0,1)，则更新之后的原型向量更接近xj。

• 若最近的原型向量pi*的类别标记与xj不同的话，则要使得pi*远离xj。

  

  

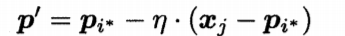
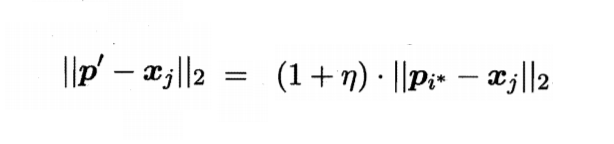
不断重复上面的步骤之后，最终学得一组原型向量{p1,p2,……,pq}，每一个原型向量代表一个簇，即可以实现对样本空间X的簇划分了。

对任意样本x，它将被划入与其距离最近的原型向量所代表的簇中；换言之，每个原型向量pi定义了与之相关的一个区域Ri，该区域中每个样本x与pi的距离不大于x与其他原型向量pi'(i'≠i)的距离，即

举例：

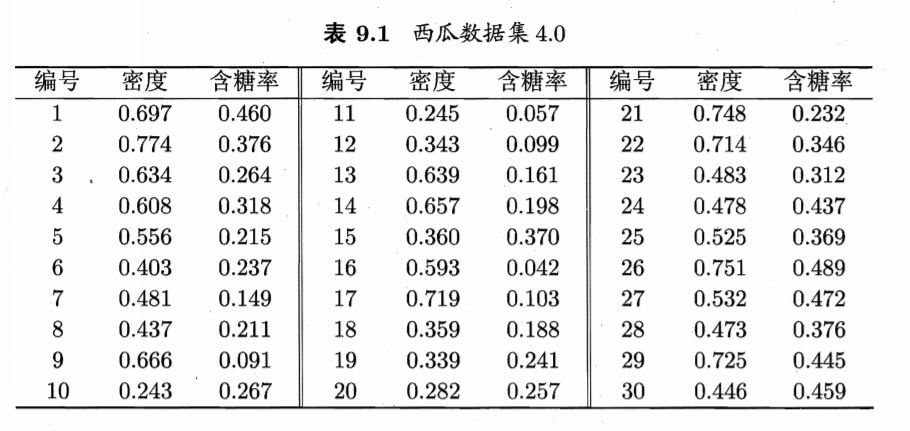
数据集

令第21号样本的类别标记为c2(好瓜=否)，其他样本的类别标记为c1(好瓜=是)。假定q=5，即学习目的是找到5个原型向量p1-p5。并假定对应的簇标记为c1,c2,c2,c1,c1即希望找到3个"好瓜=是"的簇和2个"好瓜=否"的簇。

算法开始时，根据样本的类别标记和簇的预设类别标记对原型向量进行随机初始化。假定初始化原型向量为x5,x12,x18,x23,x29。第一轮迭代中，假设随机选取到的样本为x1，该样本与原型向量x5,x12,x18,x23,x29的距离分别为0.283, 0.506, 0.434, 0.260, 0.032。由于p5即x29距离最近且两者具有相同的类别标记c2，假定学习率η=0.1，则 LVQ更新p5得到新原型向量

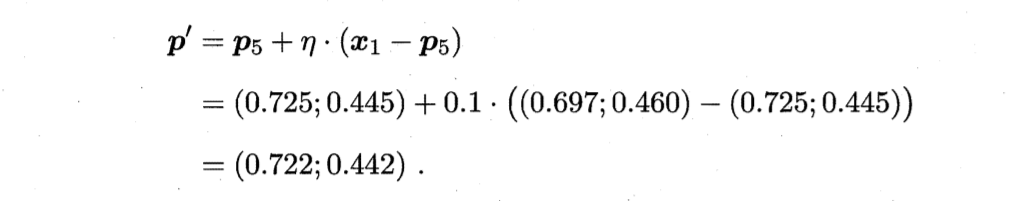
新p5

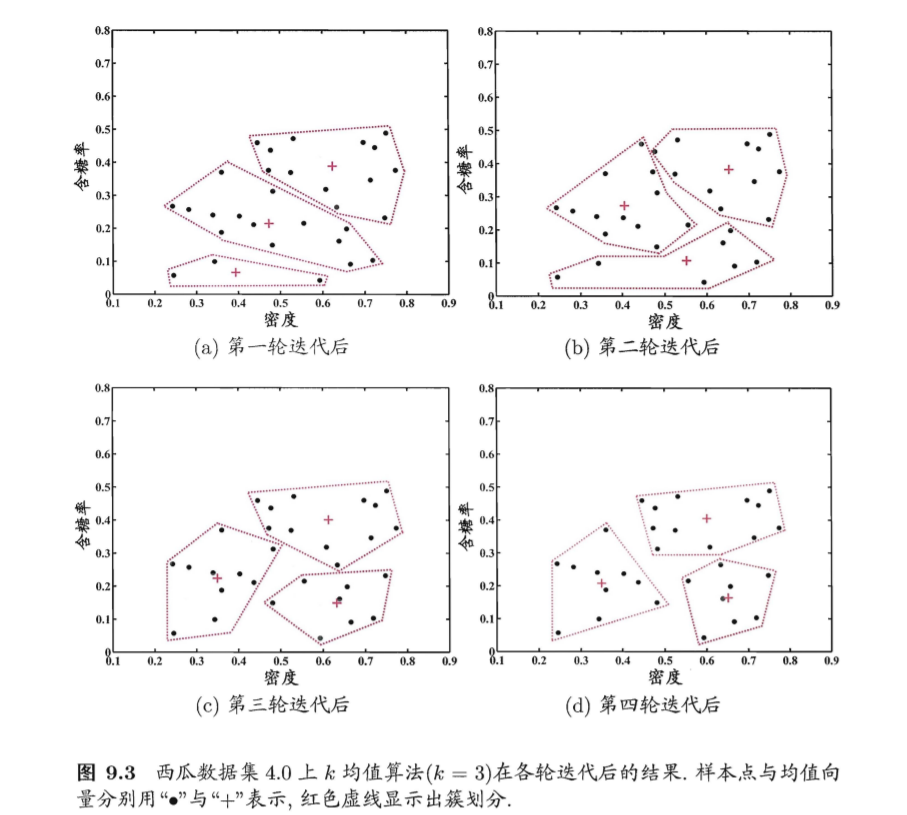
将p5更新后，不断重复上述过程。不同轮数之后的聚类结果如图。

3. 高斯混合聚类

• 高斯混合聚类原理
  对于n维样本x，服从高斯分布，概率密度函数为

  

  其中，μ为n维均值向量，Σ为n x n的协方差矩阵。关键在于Σ和μ，可以写为p(x|μi,Σi)。若有k个高斯分布混合，即高斯混合分布，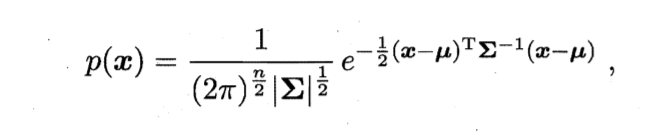

  

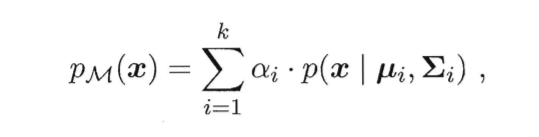
  高斯混合分布

  其中，αi>0为第i个高斯分布的参数(权重)。

  

  有数据集D，随机变量zj∈{1,2,...,k} 表示生成样本xj的高斯混合成分。zj的先验概率P(zj?= i)，对应于αi(i=1,…,k)。根据贝叶斯定理，zj的后验分布对应于

  

  将上式简写为γji，则有k个簇，每个样本xj的簇标记为λj即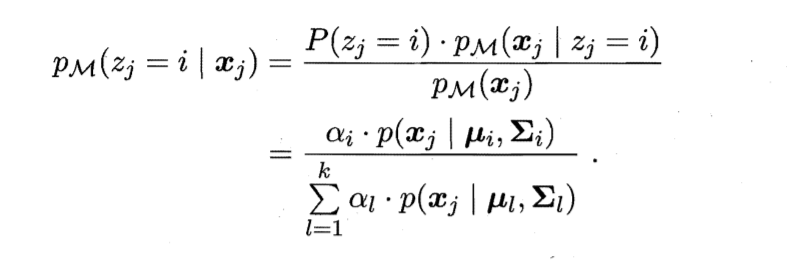

  

  对于λj，可以采用对数似然估计，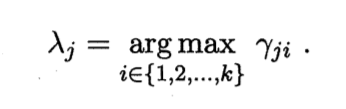

  

  上式分别对∑，μ求导，令导数为0，得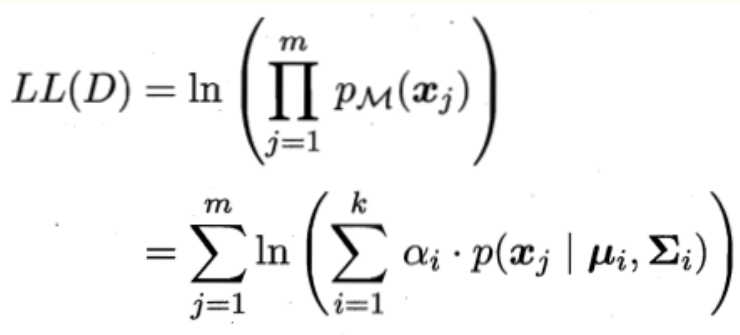

  

  α求和后为1，引入此约束，对数似然的拉格朗日形式为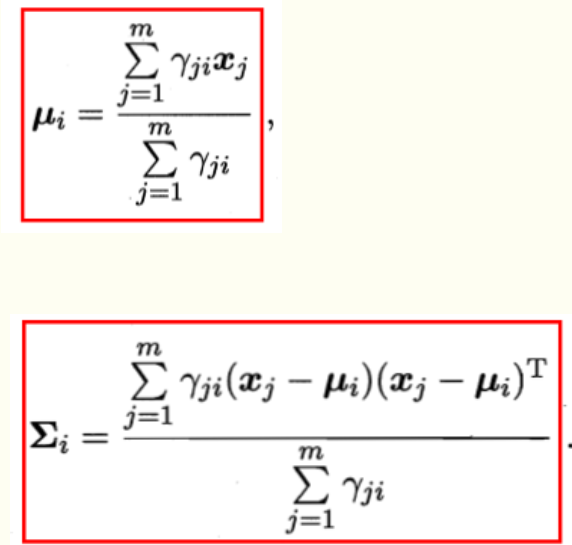

  

  上式对系数α求导，令导数为0，得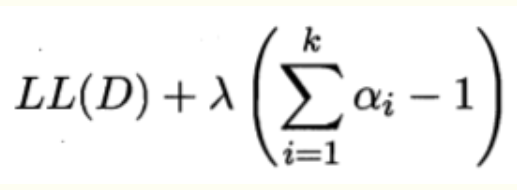

  

?

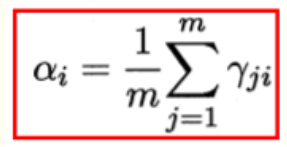
• 算法流程

  

  基于EM算法的高斯混合聚类

  第1行对高斯混合分布的模型参数进行初始化。
  第2-12行基于EM算法对模型参数进行选代更新。
  若 EM 算法的停止条件满足(例如己达到最大法代轮数，或似然函数LL(D)增长很少甚至不再增长)，
  则在第 14-17 行根据高斯混合分布确定簇划分，在第 18行返回最终结果.

• 举例

  

  

  模型参数更新后，不断重复上述过程，不同轮数之后的聚类结果如图

  

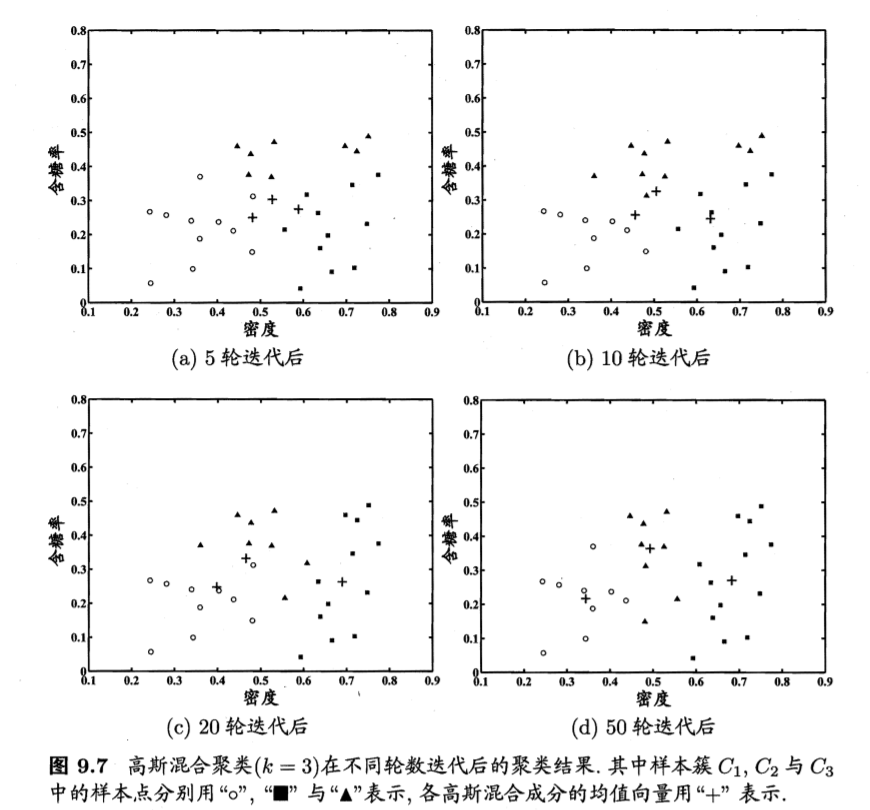
• 实现代码

# 1 读取数据
file='xigua4.txt'
x=[]
with open(file) as f:
    f.readline()
    lines=f.read().split('\n')
    for line in lines:
        data=line.split(',')
        x.append([float(data[-2]),float(data[-1])])
y=np.array(x)
# 2 算法部分
import numpy as np
import random
 
def probability(x,u,cov):
    cov_inv=np.linalg.inv(cov)
    cov_det=np.linalg.det(cov)
    return np.exp(-1/2*((x-u).T.dot(cov_inv.dot(x-u))))/np.sqrt(cov_det)
 
 
def gauss_mixed_clustering(x,k=3,epochs=50,reload_params=None):
    features_num=len(x[0])
    r=np.empty(shape=(len(x),k))
#     初始化系数，均值向量和协方差矩阵
    if reload_params!=None:
        a,u,cov=reload_params
    else:
        a=np.random.uniform(size=k)
        a/=np.sum(a)
        u=np.array(random.sample(list(x),k))
        cov=np.empty(shape=(k,features_num,features_num))
#         初始化为只有对角线不为0
        for i in range(k):
            for j in range(features_num):
                cov[i][j]=[0]*j+[0.5]+[0]*(features_num-j-1)
    step=0
    while step<epochs:
#         E步：计算r_ji
        for j in range(len(x)):
            for i in range(k):
                r[j,i]=a[i]*probability(x[j],u[i],cov[i])
            r[j]/=np.sum(r[j])
             
        for i in range(k):
            r_toal=np.sum(r[:,i])
            u[i]=np.sum([x[j]*r[j,i] for j in range(len(x))],axis=0)/r_toal
            cov[i]=np.sum([r[j,i]*((x[j]-u[i]).reshape((features_num,1)).dot((x[j]-u[i]).reshape((1,features_num)))) for j in range(len(x))],axis=0)/r_toal
            a[i]=r_toal/len(x)
        step+=1
    C=[]
    for i in range(k):
        C.append([])
    for j in range(len(x)):
        c_j=np.argmax(r[j,:])
        C[c_j].append(x[j])
    return C,a,u,cov

参考链接:https://www.cnblogs.com/lunge-blog/p/11792226.html

9.5 密度聚类

密度聚类亦称"基于密度的聚类"，此类算法假设聚类结构能通过样本分布的紧密程度确定。

DBSCAN是一种代表性聚类算法，基于一组"领域"参数(ε,m)来刻画样本分布的紧密程度。给定数据集D={x1,x2,……,xm}。有以下几个概念

• ε-领域
  对xj∈D，其ε-邻域包含样本集D中与xj的距离不大于ε的样本，即在数据集D中，所有除xj的样本到xj的距离小于ε的样本集合。

  

  这里的dist()默认为欧氏距离。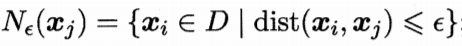

• 核心对象
  若xj的ε-邻域至少包含m个样本，即

  

  则xj是一个核心对象。即如果样本点xj的ε-邻域中包含的样本个数大于等于指定值m，则该点xj称为核心点。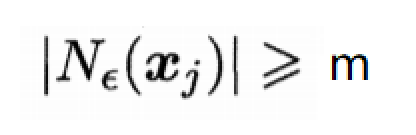

• 密度直达
  若xj位于xi的ε-邻域中，且xi是核心对象，则称xj由xi密度直达。

• 密度可达
  对xi与xj，若存在样本序列p1,p2,...,pn，其中p1=xi，pn=xj且pi+1由pi密度直达，则称xj由xi密度可达。

• 密度相连
  对xi与xj，若存在xk使得xi与xj均由xk密度可达，则称xi与xj密度相连。

  

  

?

DBSCAN就是将数据集中的密度可达的所有样本点划分为一个簇，某些样本密度可达形成一个簇，另外一些样本点又可以密度可达就又形成另外一个簇。簇内样本点均密度可达，但是簇内的样本点与其他簇的样本点无法可达，最后形成了多个簇类。

算法流程如下

在第1-7行中，算法先根据给定的领域参数(ε,m)找出所有核心对象。
第10-24行，以任一核心对象为出发点，找出由其密度可达的样本生成聚类簇，直到所有核心对象均被访问过为止。

简易流程描述如下
1）如果一个点p的ε-邻域包含多于m个样本，则创建一个以p为核心对象的新簇。
2）寻找并合并核心对象直接密度可达的样本点。
3）没有新点可以更新簇时，算法结束。

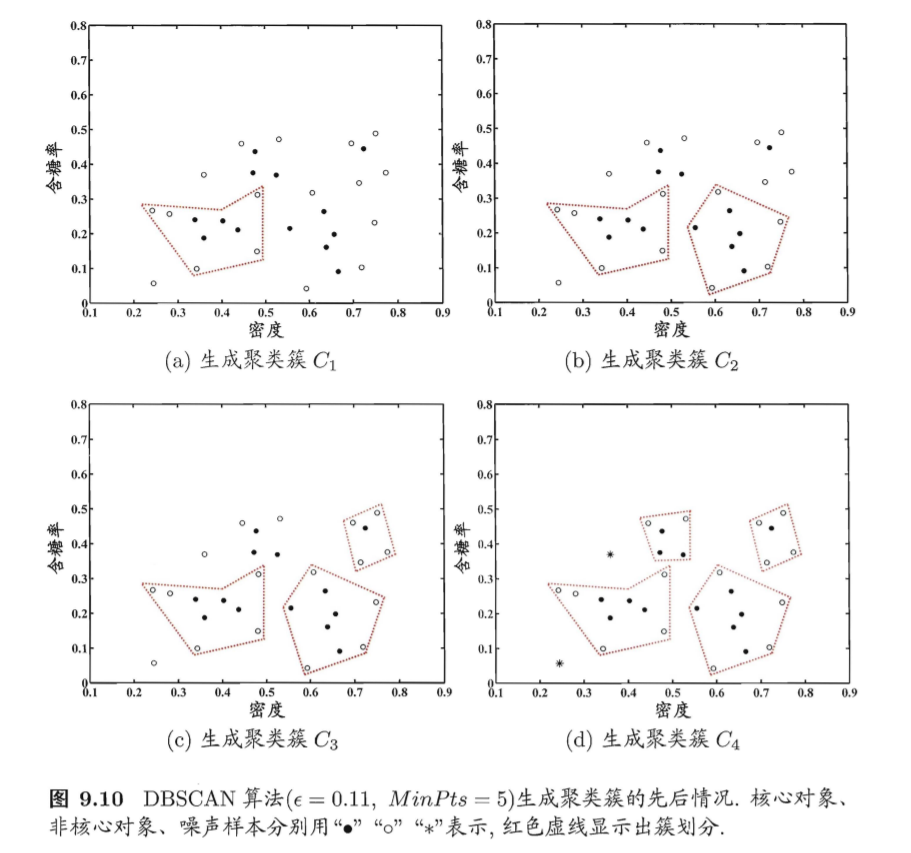
举例

生成的簇如图

import numpy as np
epsilon = 0.11
minpts = 5
x = np.load("watermalon4.0.npy")
#epsilon邻域统计表
t = [set() for i in range(30)]
#聚类簇
clusters = []
#核心对象集
coreset = set()
for i in range(len(x)):
    t[i].add(i)
    for j in range(i+1,len(x)):
        #欧式距离
        dist = np.linalg.norm(x[i] - x[j])
        if dist <= epsilon:
            #记录epsilon邻域信息
            t[i].add(j)
            t[j].add(i)
for i in range(len(t)):
    if len(t[i]) >= minpts:
        #核心对象集
        coreset.add(i)
allset = {i for i in range(len(x))}
while len(coreset) > 0:
    #浅拷贝（拷贝第一层，这里没影响）
    oldset = allset.copy();
    corepoint = coreset.pop()
    q = [corepoint]
    allset -= {corepoint}
    while len(q) > 0:
        item = q.pop(0)
        if len(t[item]) >= minpts:
            #交集
            delta = t[item] & allset
            q += [i for i in delta]
            allset -= delta
    #新的聚类簇
    newcluster = oldset - allset
    clusters.append(newcluster)
    coreset -= newcluster
print(clusters)

代码2

代码链接：https://blog.csdn.net/weixin_35732969/article/details/81291670
https://www.cnblogs.com/hiyoung/p/9821589.html

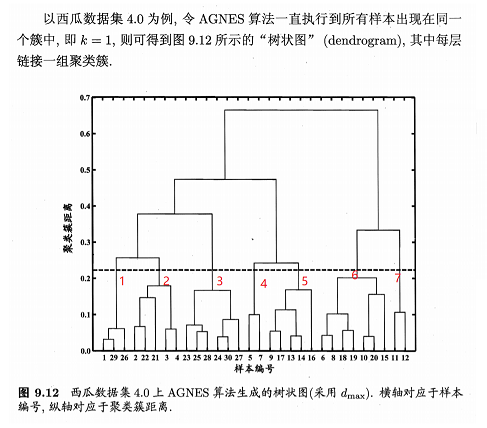
9.6 层次聚类

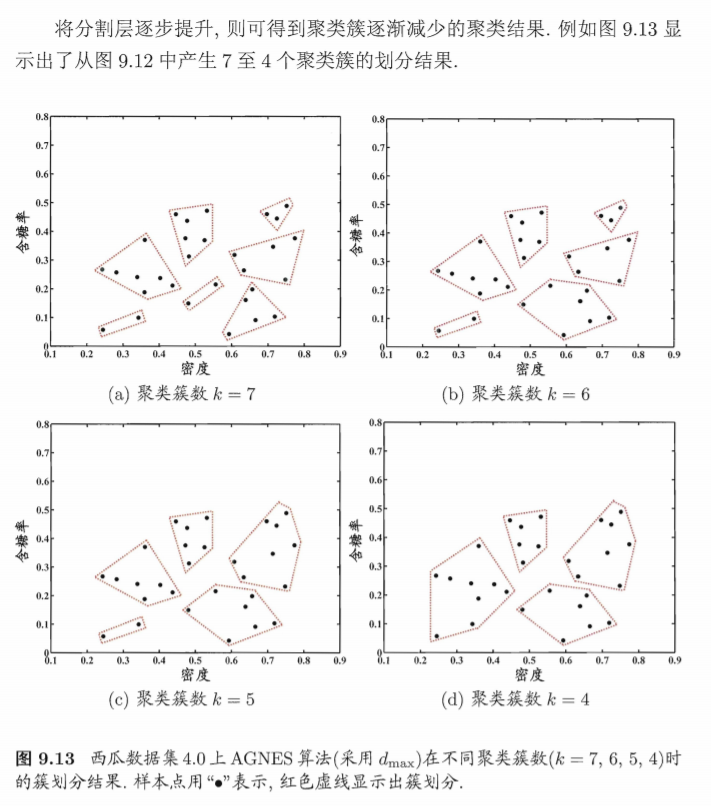
层次聚类是聚类算法的一种，试图在不同层次对数据集进行划分，从而形成聚类树结构。在聚类树中，不同类别的原始数据点是树的最低层，树的顶层是一个聚类的根节点。数据集的划分有自下而上聚合策略和自上而下分裂两种方法。这里只讲解聚合策略。

AGNES是一种自下而上的聚合策略。先将每个样本作为一个初始簇，然后在算法运行的每一步中合并两个距离最近的初始簇为越来越大的簇，直到达到预设的聚类簇个数。
简单的流程如下
(1) 将每个样本看作初始簇，计算两两之间的最小距离；
(2) 将距离最小的两个簇合并成一个新簇；
(3) 重新计算新簇与所有簇之间的距离；
(4) 重复(2)、(3)，直到达到停止条件。

该算法的关键在于如何计算聚类簇之间的距离。
实际上每个簇是一个样本集合，因此，只需采用关于集合的某种距离即可。例如，给定聚类簇Ci与Cj，可通过下面的式子来计算距离:

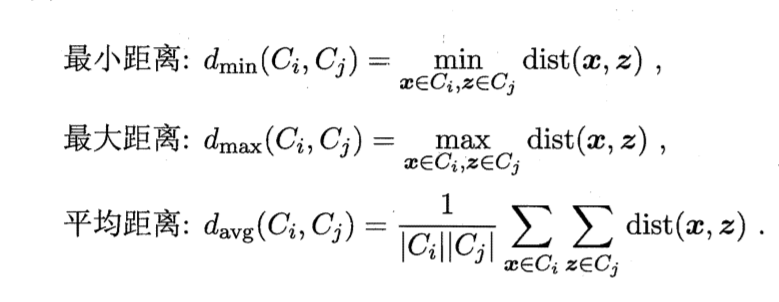
最小距离由两个簇的最近样本决定，最大距离由两个簇的最远样本决定，平均距离则由两个簇的所有样本共同决定。当聚类使用dmin，dmax或davg计算时，AGNES算法称为"单链接"、"全链接"或"均链接"算法。

在第1-9行，算法先对仅含一个样本的初始聚类簇和相应的距离矩阵进行初始化;
第11-23行，AGNES不断合并距离最近的聚类簇，并对合并得到的聚类簇的距离矩阵进行更新;
上述过程不断重复，直到达到预设聚类簇。

举例

代码实现

# 现有数据集circle.xls。样本具有以下几个特征：基站编号、工作日上班时间人均停留时间、凌晨人均停留时间、周末人均停留时间、日均人流量，
# 要求根据以上维度指标，对数据集进行层次聚类，同时要求打印输出样本的类别标签，并画出谱系聚类图。
import pandas as pd
import scipy.cluster.hierarchy as sch
from sklearn.cluster import AgglomerativeClustering
from sklearn.preprocessing import MinMaxScaler
from matplotlib import pyplot as plt
# 读取数据
data = pd.read_excel(r'circle.xls',index_col='基站编号')
# print(data.head())
df = MinMaxScaler().fit_transform(data)

# 建立模型
model = AgglomerativeClustering(n_clusters=3)
model.fit(df)
data['类别标签'] = model.labels_
print(data.head())

# 画图
ss = sch.linkage(df,method='ward')
sch.dendrogram(ss)
plt.show()

原文链接：https://blog.csdn.net/qq872890060/article/details/100019662

0人点赞

机器学习