如有转载,请注明出处
常用激活函数列表
| name | plot | equation |
|---|---|---|
| sigmoid | 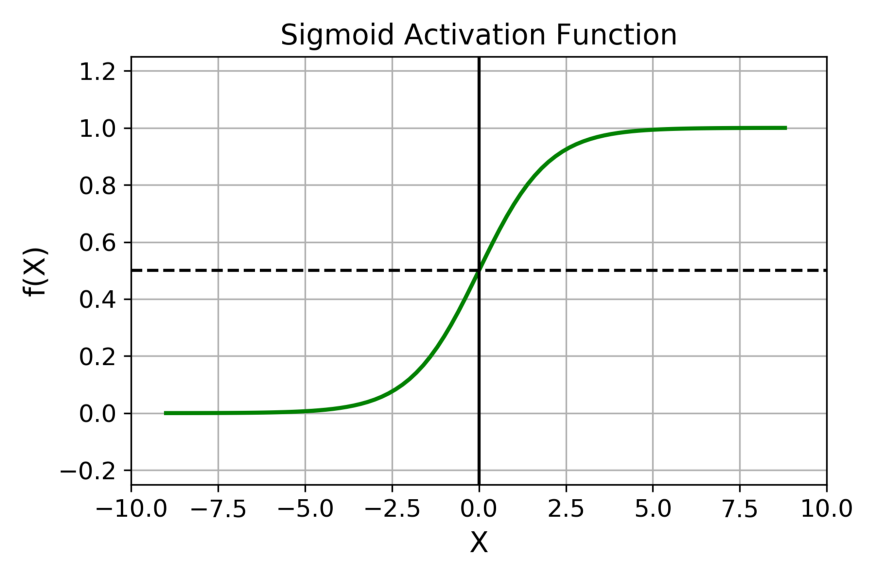 | f ( x ) = 1 1 + e ? x f(x) = \frac{1}{1+e^{-x}} f(x)=1+e?x1? |
| Tanh | 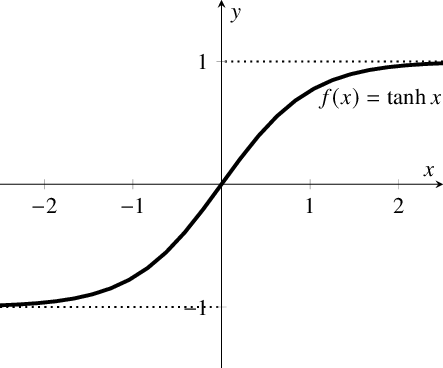 | f ( x ) = t a n h ( x ) = 2 1 + e ? 2 x = 2 s i g m o i d ( 2 x ) ? 1 f(x)=tanh(x)=\frac{2}{1+e^{-2x}} \\ = 2sigmoid(2x)-1 f(x)=tanh(x)=1+e?2x2?=2sigmoid(2x)?1 |
| ReLU | 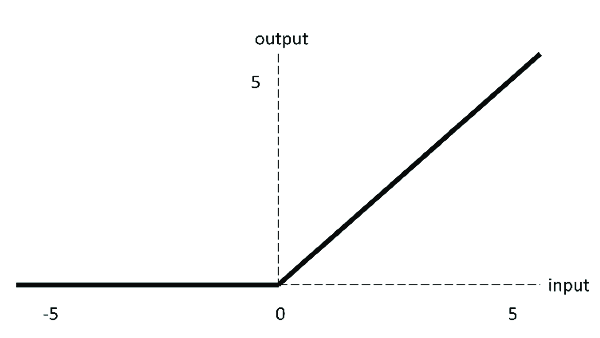 | f ( x ) = m a x ( 0 , x ) f(x)=max(0,x) f(x)=max(0,x) |
| Leaky ReLU | 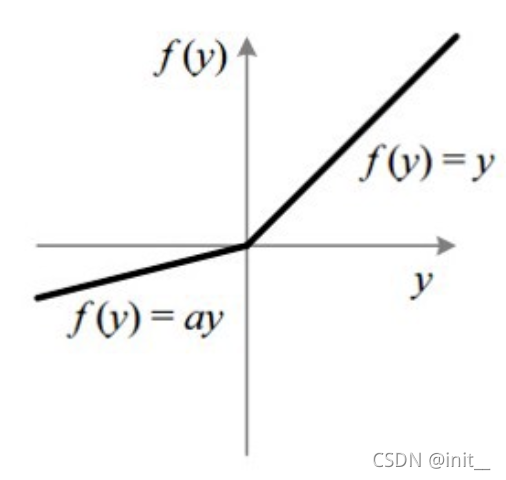 | 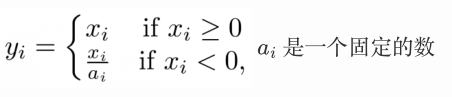 |
| PReLU | 可以看作是Leaky ReLU的一个变体。在PReLU中,负值部分的斜率是根据数据来定的 | |
| RReLU | 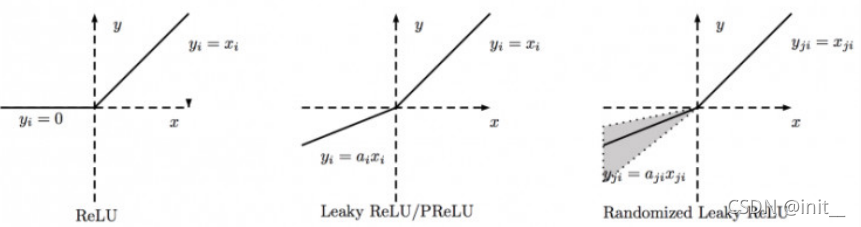 | RReLU也是Leaky ReLU的一个变体。在RReLU中,负值的斜率在训练中是随机的,在之后的测试中就变成了固定的了。RReLU的亮点在于,在训练环节中, a j i a_{ji} aji?是从一个均匀的分布U(I,u)中随机抽取的数值。 |
| Swish | 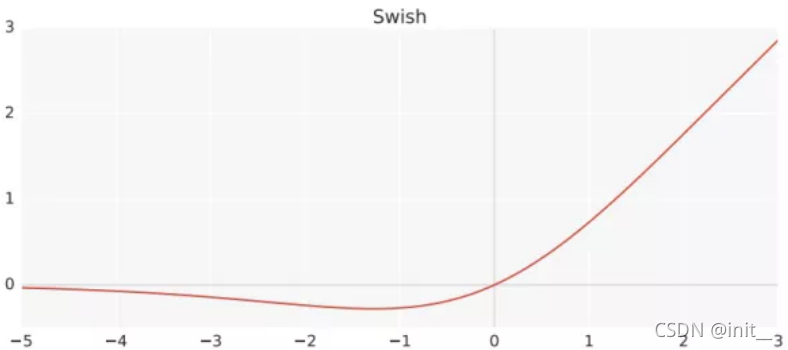 | s w i s h ( x ) = x ? σ ( x ) swish(x) = x \cdot \sigma (x) swish(x)=x?σ(x) |
| Mish | 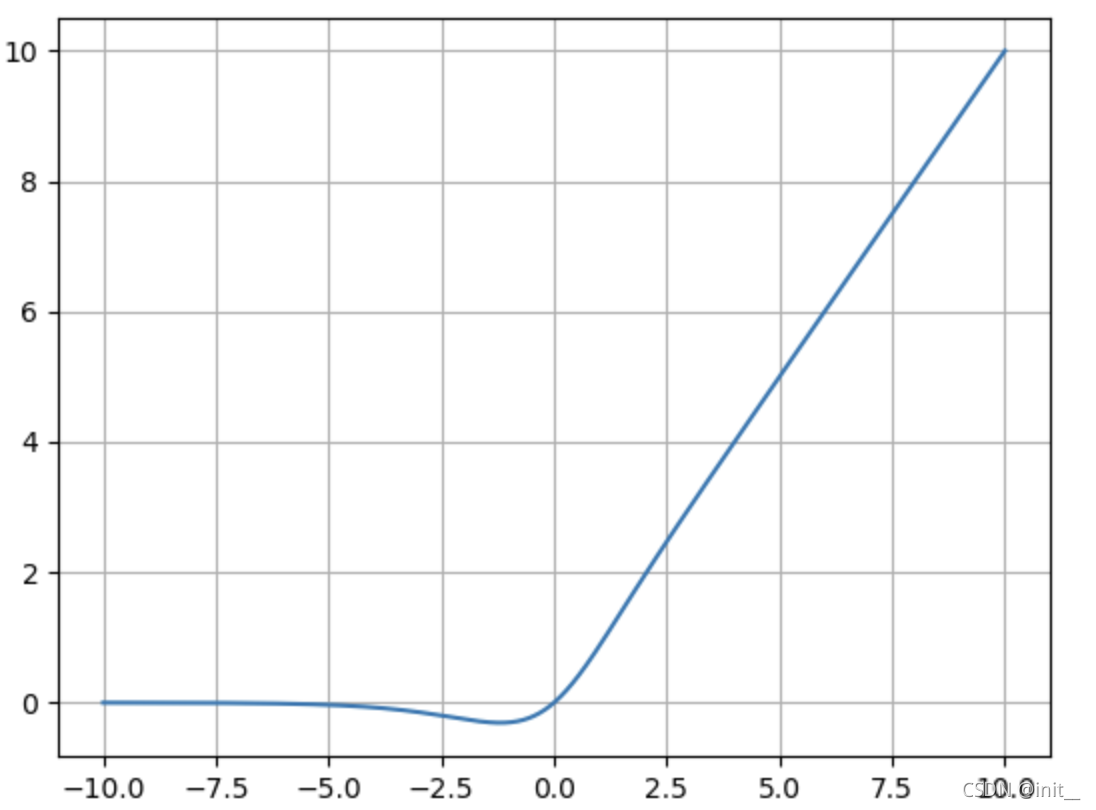 | m i s h ( x ) = x ? t a n h ( s o f t p l u s ( x ) ) mish(x)= x \cdot tanh(softplus(x)) mish(x)=x?tanh(softplus(x)) |
常用激活函数介绍
sigmoid
早期的激活函数大多采用sigmoid函数,但是它存在一些问题:
- 过大或者过小的结果都会导致梯度趋近于0,再经过多层,梯度还会进行N次方操作,其结果就更小。这很容易就导致梯度弥散。这也是早期的神经网络都不深的原因。
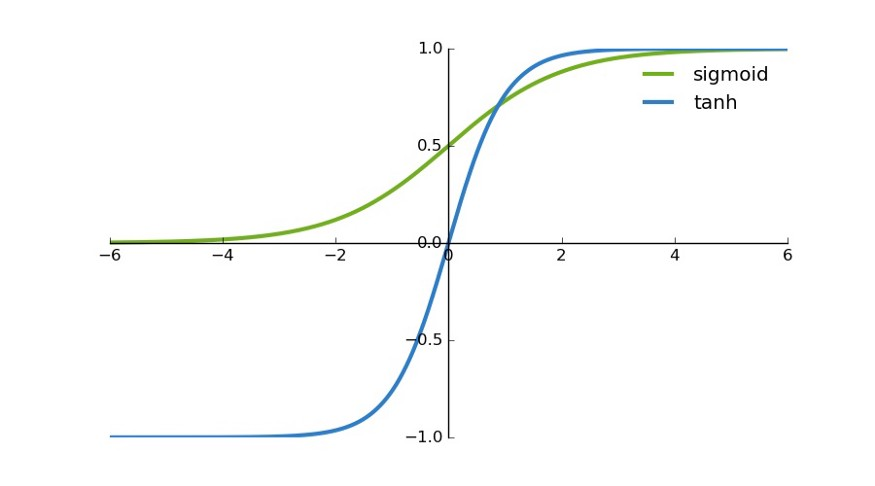
- 相比于tanh。可以看出sigmoid 的 区间为(0, 1);tanh的区间为(-1, 1)。sigmoid 会 使得结果一直为正。那么在反向传播时,经过同一个神经元传播而来的,多个参数的梯度总是同号的。其梯度的方向取决于同一个数,(如果是二维的)其梯度应在一三象限内移动,如果初始位置不佳,很容易导致zigzag。具体内容可参阅在神经网络中,激活函数sigmoid和tanh除了阈值取值外有什么不同吗?
ReLU
由于sigmoid、tanh的饱和区导数为0,导致网络不能做的很深。而ReLU的诞生,一定程度上解决了网络深度的问题。ReLU是分段线性函数,其非线性性很弱,因此网络一般都需要做的比较深。而这正迎合了当今的需求,在同样效果的前提下,往往深度比宽度更重要,更深的模型泛化能力更好。是当今最常用的激活函数。
ReLU 在 x < 0 x < 0 x<0 时,其梯度为0,会导致Dead ReLu的问题。而Leaky ReLU/PReLU/RReLU都是ReLU的变体,都是使得 x < 0 x<0 x<0时给他较小的梯度,解决了Dead ReLu的问题,但在实际操作中,尚未能证明,leaky RELU总是优于RELU。
Swish 与 Mish
Swish , mish 的plot都类似,在神经网络中取得了优于RELU的效果,但是背后的原因目前没有理论和实验的证明。
参考苏剑林大神的说法:
-
Swish,mish在0点处是可微分的,且在0附近均有一定的梯度信息,在远小于0处其梯度结果为0
-
Xavier、Kaiming初始化都是在0附近的正态分布或均匀分布。如果使用ReLu会导致一半的参数梯度为0