[人工智能]低差异序列--基于Halton序列的采样

在使用蒙特卡洛方法时，需要对设计变量空间的样本点进行采样，采集的样本点在空间的分布情况的好坏，可以对收敛速度产生影响，基于蒙特卡洛方法使用的是伪随机序列，基于准蒙特卡洛方法使用的是低差异序列如Halton 序列、Sobol 序列或 Faure 序列。

理论上准蒙特卡洛的低差异序列收敛速度更快，基于低差异序列的采样在空间分布均匀性能够达到拉丁超立方采样的性能。

这里给出Halton序列采样的matlab代码示例，具体关于Halton序列的原理见下面链接

https://zhuanlan.zhihu.com/p/20197323

clear
clc
%基于Halton序列的采样，关于这方面的知识查看https://zhuanlan.zhihu.com/p/20197323

npoints=100;
ndv=2;  %维数
Binary=[];  %暂时每一维存储10进制整数转换后的二进制


A=[randperm(npoints);randperm(npoints)];  %得到每一维的npoints个整数
B=[2;7];   %存储每一维需要转换的进制，维数之间转换的进制需要互质

for i=1:ndv
    for j=1:npoints 
 %%  这里是将每一个整数转换成二进制
        C=jinzhizhuanhuan(A(i,j),B(i,:))
 %%  高位补零，以便对每一个整数转换成二进制后，位数一致，方便矩阵计算
        if length(C)<npoints
            C=[zeros(1,npoints-length(C)),C];
        end
        Binary=[Binary;C];  %得到关于每一维nopints个整数最终的二进制的矩阵，每一行代表一个整数的进制表示
    end
    Binary_end(:,:,i)=Binary;  %得到ndv维的每个整数的二进制矩阵，Binary_end(:,:,1)代表第1维的npoints个点转换进制后的矩阵
    Binary=[];
end
clear i j;
%% 这里是为了将二进制，镜像翻转到小数位，在对其进行十进制运算
D = fliplr(Binary_end);  % 将矩阵按行翻转

%% 将镜像翻转到小数点后的进制表示转换成十进制得到最终的结果
for i=1:ndv
    for j=1:npoints
        E(i,j)=B(i,:)^(-j);
    end
    F(i,:)=E(i,:)*(D(:,:,i))';   %为了矩阵乘法运算正好可以计算最终的十进制值
end

%% 画出散点图
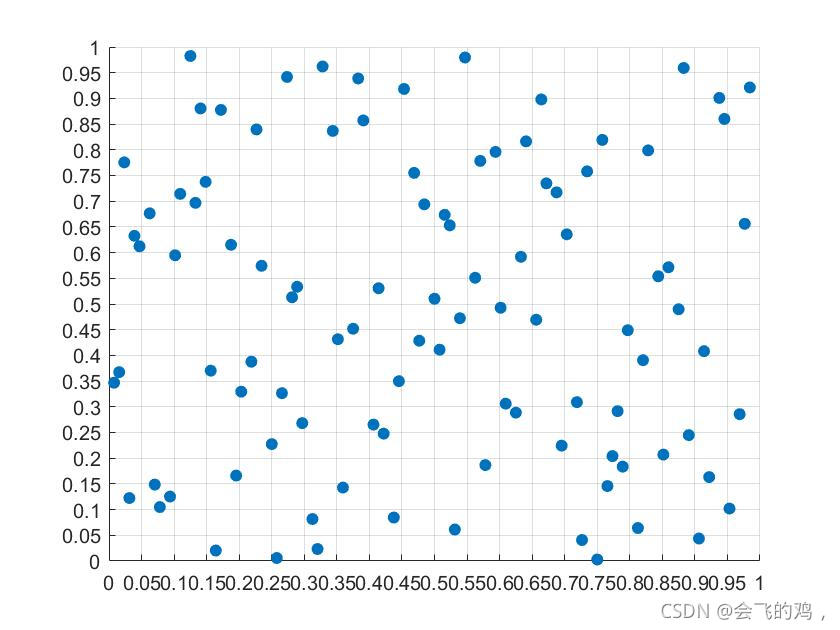
scatter(F(1,:),F(2,:),'filled')
grid on
xticks(0:1/20:1);
yticks(0:1/20:1);

进制转换函数如下：

function Base = jinzhizhuanhuan(n,N)
% 进制转换，目的是为了将十进制整数n转化成N进制，N<10
Base=[];
%辗转相除法转换进制
while floor((n/N))>0    %floor向下取整
    Base=[Base,mod(n,N)];
    n=floor(n/N);
end
Base=fliplr([Base,n]);
return
end

?结果如下：由于具有随机性，每次运行结果并不一致。

?