数据分析之numpy篇
文章目录
numpy简介
设么是numpy?
一个在python中做科学计算的基础库,重在数值计算,也是大部分python科学计算库的基础库,多用在大型、多维数组上执行数值运算。
数据类型相关
import numpy as np
import random
#使用numpy生成数组,得到ndarray的类型
t1 = np.array([1, 2, 3])
print(t1)
print(type(t1))
t2 = np.array(range(10))
print(t2)
print(type(t2))
t3 = np.arange(4, 18, 3)
print(t3)
print(type(t3))
print(t3.dtype)
#numpy中的数据类型
t4 = np.array(range(1, 4), dtype="float32")
print(t4)
print(t4.dtype)
#numpy中的bool类型
t5 = np.array([1, 0, 1, 0, 0, 0, 1, 1, 1], dtype=bool)
print(t5)
print(t5.dtype)
#调整数据类型
t6 = t5.astype("int8")
print(t6)
print(t6.dtype)
#numpy中的小数类型
t7 = np.array([random.random() for i in range(6)])
print(t7)
print(t7.dtype)
t8 = np.round(t7, 3)
print(t8)
数组的形状
import numpy as np
#查看数组的形状 shape
t1 = np.arange(12)
print(t1)
print(t1.shape)
t2 = np.array([[1, 2, 3], [4, 5, 6]])
print(t2)
print(t2.shape)
print("行", t2.shape[0])
print("列", t2.shape[1])
t3 = np.array([[[1, 2, 3], [4, 5, 6]], [[7, 8, 9], [2, 9, 0]]])
print(t3)
print(t3.shape)
#修改数组的形状 reshape()
t4 = np.arange(24)
print(t4)
t5 = t4.reshape((4, 6))
print(t5)
print(t5.shape)
t6 = t4.reshape((3, 2, 4))
print(t6)
print(t6.shape)
#按行展开 .flatten()
t7 = t6.flatten()
print(t7)
print(t7.shape)
数组的计算
数组与数组之间进行加减乘除运算时,满足以下原则:
广播原则:如果两个数组的后缘维度(trailing dimension,即从末尾开始算起的维度)的轴长度相符或其中一方的长度为1,则认为它们是广播兼容的。广播会在确实和(或)长度为1的维度上进行。
简单来说,就是两个数组的shape后几位必须相符合。
import numpy as np
t1 = np.arange(10, 34).reshape(4, 6)
print(t1)
#加k
t2 = t1 + 2
print(t2)
t3 = np.arange(100, 124).reshape(4, 6)
#加减乘除相同形状大小矩阵
t4 = t1 + t3
print(t4)
t5 = t1 - t3
print(t5)
t6 = t1 * t3
print(t6)
t7 = t1 / t3
print(t7)
t8 = t3 // t1
print(t8)
t9 = np.arange(0, 6) ** 2
print(t9)
#与相同行或者列数组进行运算(每一组都将参与运算)
a1 = np.arange(10, 34).reshape(4, 6)
a2 = np.arange(0, 6)
a3 = np.arange(4).reshape(4, 1)
a5 = a1 - a2
print(a5)
a6 = a1 - a3
print(a6)
numpy转置
轴(axis):在numpy中可以理解为方向,使用0,1,2…数字表示,对于一个一维数组,只有一个0轴,对于2维数组(shape(2,2)),有0轴和1轴,对于三维数组(shape(2,2,3)),有0,1,2轴。
transpose 或 T 或 交换轴
t1 = np.arange(12).reshape(3, 4)
#矩阵的转置 transpose 或 T 或 交换轴
t2 = t1.transpose()
t3 = t1.T
t4 = t1.swapaxes(1, 0)
numpy索引和切片
a1 = np.arange(48).reshape(6, 8)
print(a1)
#取行
print(a1[2])
#取连续的多行
print(a1[4:])
#取不连续的多行
print(a1[2::2])
print(a1[[0, 3, 4]])
#取列
print("取列: ", a1[:,1])
print("取3列及其以后列元素:\n", a1[:,2:])
print("取3,5,6列:\n", a1[:,[2, 4, 5]])
#取多行多列, 取第3行,第4列的值
print(a1[2, 3])
print(type(a1[2,3])) #<class 'numpy.int32'>
#取多行多列, 取第3行到地5行, 第2列到第4列的元素(交叉元素)
print(a1[2:5, 1:4])
#取多个不相邻的点(0, 0) (2, 1), (4, 5)
b = a1[[0,2,4], [0,1,5]]
print(b)
数值修改和bool索引
在对应索引切片处赋值即可
import numpy as np
a = np.arange(48).reshape(6, 8)
print(a)
b1 = a < 10
print(b1)
a[a < 10] = 123
print(a)
a[[2, 3, 4],[0, 1, 3]] = 1
print(a)
b2 = a
b2[b2 < 10] = 0
b2[b2 > 10] = 10
print(b2)
三元运算符where
a = np.arange(48).reshape(6, 8)
print(a)
b = a
b[b < 20] = 0
b[b >= 20] = 100
print(b)
#即将小于20赋值为0, 大于等于20 赋值为100
#使用 三元运算符 等价于
c = a
np.where(c < 20, 0, 100)
print(c)
裁剪clip
a = np.arange(48).reshape(6, 8)
print(a)
#将小于15的替换为15,大于30的替换为30
b = a.clip(15, 30)
print(b)
数组的拼接
np.vstack((t1, t2))#竖直拼接np.hstack((t1, t2))#水平拼接
t1 = np.arange(12).reshape(2, 6)
t2 = np.arange(24, 36).reshape(2, 6)
print("t1\n{}".format(t1))
print("t2\n{}".format(t2))
t3 = np.vstack((t1, t2)) #竖直拼接
t4 = np.hstack((t1, t2)) #水平拼接
print("t1 和 t2 竖直拼接\n {}".format(t3))
print("t1 和 t2 水平拼接\n {}".format(t4))
分割时方向恰恰与拼接相反
数组的行列交换
索引赋值即可
a = np.arange(48).reshape(6, 8)
print(a)
#行交换
a1 = a
a1[[1, 2],:] = a1[[2, 1],:]
print(a1)
#列交换
a2 = a
a2[:,[3, 7]] = a2[:,[7, 3]]
print(a2)
最值、全0/1数组、I/E
- 获取最大值和最小值的位置
np.argmax(t.axis=0)np.argmin(t.axis=1)
- 创建一个全0的数组:
np.zeros((3,4)) - 创建一个全1的数组:
np.ones((3,4)) - 创建一个对角线为1的正方形数组(方阵):
np.eys(3)
import numpy as np
import random
a = np.array([random.randint(0, 100) for i in range(32)]).reshape(4, 8)
print(a)
a1 = np.argmax(a, axis=0)
print("行最大值位置:\n{}".format(a1))
a2 = np.argmax(a, axis=1)
print("列最大值位置:\n{}".format(a2))
#创建全0数组
a3 = np.zeros((3, 4))
print("全0数组:\n {}".format(a3))
#创建全1数组
a4 = np.ones((3, 4))
print("全1数组:\n {}".format(a4))
#创建一个对角线为1的正方形数组(方阵)
a5 = np.eye(6)
print("单位矩阵:\n {}".format(a5))
a6 = a5 * (-1)
print(a6)
numpy生成随机数
| 参数 | 解释 |
|---|---|
.rand(d0,d1,..dn) | 创建d0-dn维度的均匀分布的随机数数组,浮点数,范围从0-1 |
.rand(d0,d1,..,dn) | 创建d0-dn维度的标准正态分布随机数,浮点数,平均数0,标准差1 |
.randint(low,high,(shape)) | 从给定上下限范围选取随机数整数,范围是low,high, 形状是shape |
.uniform(low,high,(size)) | 产生具有随机分布的数组,low起始值,high结束值,size形状 |
.normal(loc,scale,(size)) | 从指定正态分布中随机抽取样本,分布中心是loc(概率分布的均值),标准差是scale,形状是size |
.seed(s) | 随机数种子,s是给定的种子值。因为计算机生成的是伪随机数,所以通过设定相同的随机数种子,可以每次生成相同的随机数 |
numpy的copy和view
a = b完全不复制,a和b相互影响a = b[:],视图的操作,一种切片,会创建新的对象a,但是a的数据完全由b保管,它们的数据变化是一致的a = b.copy(),复制,a和b互不影响
import numpy as np
np.random.seed(10)
a = np.random.randint(10, 20, (5, 8))
print(a)
b = a[3:, 3:]
print("b = a[3:]\n", b)
b += 1000
print("a的变化: \n", a)
print("b的变化:\n", b)
c = a.copy()
c -= 1000
print("c = a.copy() - 1000: \n", c)
print("a的值:\n", a)
numpy中的nan和inf
nan(NAN,Nan):not a number 表示不是一个数组
什么时候numpy中会出现nan:
- 当我们读取本地文件为float的时候,如果有缺失,就会出现nan
- 当做了一个不合适的计算的时候(比如无穷大(inf)减去无穷大)
inf(-inf.inf):infinity, inf表示正无穷, -inf表示负无穷
什么时候会出现inf包括(-inf,+inf)
- 比如一个数字除以0,(python中直接会报错,numpy中是一个inf或者-inf)
如何制定一个nan或者inf:
d = np.inf
print(type(d))
e = np.nan
print(type(e))
nan的注意点
-
两个nan是不相等的
np.nan != np.nan(True) -
可以利用以上特性,判断数组中nan的个数
np.count_nonzero(t != t) -
如何判断一个数字是否是nan呢,通过
np.isnan(a)来判断,返回bool类型,比如希望吧nan替换为0t[np.isnan(t)] = 0
-
nan和任何值计算都为nan
print(np.nan != np.nan)
f = np.array([[1.9, 2.7, np.nan], [np.nan, np.nan, 4.9]])
print(f)
nan_counts = np.count_nonzero(f != f)
print(nan_counts)
f1 = f.copy()
f1[np.isnan(f1)] = 0
print(f1)
f2 = f.copy()
f2 -= np.nan
print(f2)
numpy中的常用统计函数
| 作用 | 函数 |
|---|---|
| 求和 | t.sum(axis=Node) |
| 均值 | t.mean(axis=None)受离群点的影响较大 |
| 中值 | np.median(t.axis=None) |
| 最大值 | t.max(axis=None) |
| 最小值 | t.min(axis=None) |
| 极差 | np.ptp(t.axis=None)即最大值和最小值的差 |
| 标准差 | t.tsd(axis=None) |
默认返回多维数组的全部统计结果,如果指定axis,则返回一个当前轴上的结果
import numpy as np
a = np.arange(24).reshape(4, 6)
print(a)
print("求和:\n", a.sum(axis=0))
print("求均值: \n", a.mean())
print(a.mean(axis=1))
print("中值:\n", np.median(a, axis=1))
print("最大值:\n", a.max())
print("最小值:\n", a.min(axis=0))
print("极差:\n", np.ptp(a, axis=1))
print("标准差: \n", a.std())
小练习:将nan赋值为mean()
import numpy as np
def fill_ndarray(a):
for i in range(a.shape[1]):
temp_col = a[:, i]
nan_num = np.count_nonzero(temp_col != temp_col)
if nan_num != 0: #不为0, 说明当前这一列中有nan
temp_not_nan_clo = temp_col[temp_col == temp_col]
#选中当前为nan的位置,并将其赋值为不是nan的均值
temp_col[temp_col != temp_col] = temp_not_nan_clo.mean()
return a
if __name__ == '__main__':
a = np.arange(24).reshape(4, 6).astype("float")
print(a)
a[1:3, 2:5] = np.nan
print(a)
a = fill_ndarray(a)
print("赋值nan为列均值: \n", a)
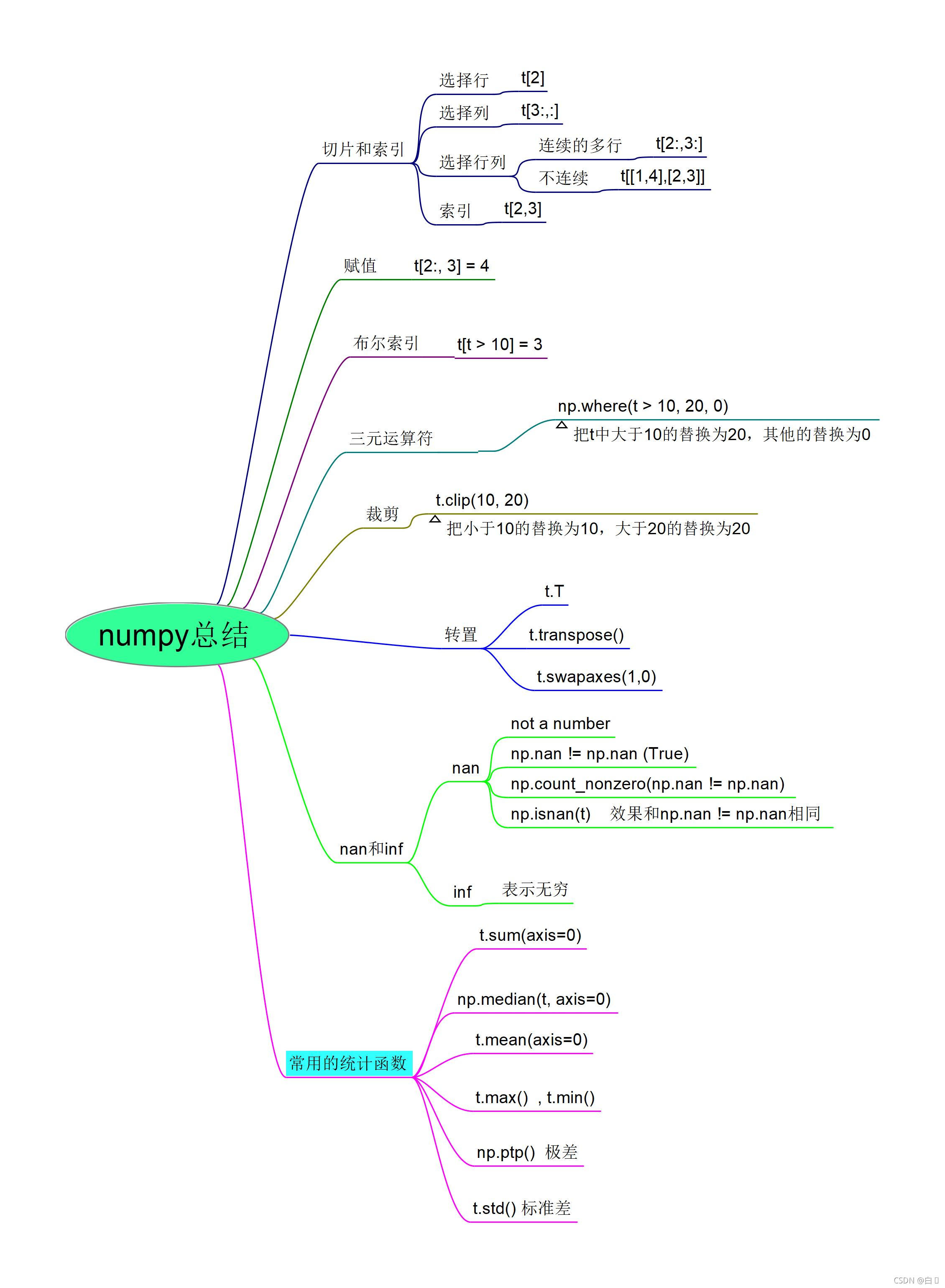
总结