由于普通的拉丁超立方采样,样本点序列是一个随机的排列,就会出现如下分布状况,虽然采样点满足了空间投影均匀的特性,但它的空间填充效果并不好。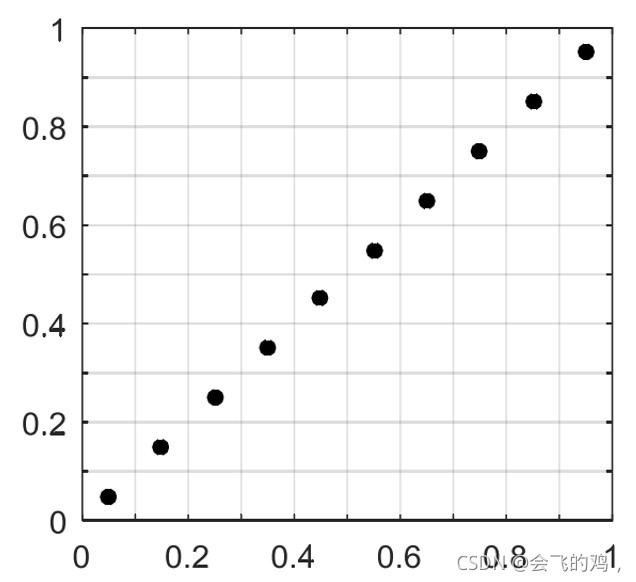
?根据参考文献的那篇论文提出的最大最小方法优化普通拉丁超立方采样。论文中阐述了最大最小的方法是,对于每一个样本点,它与之前几个样本点的距离最小值为该样本点的特征距离,而优化的目的是为了使这个特征距离最大,让样本点之间更加离散充满整个空间而不是聚集在一起。
下面引用一个例子介绍一下关于二维设计变量空间如何利用最大最小方法优化拉丁超立方采样。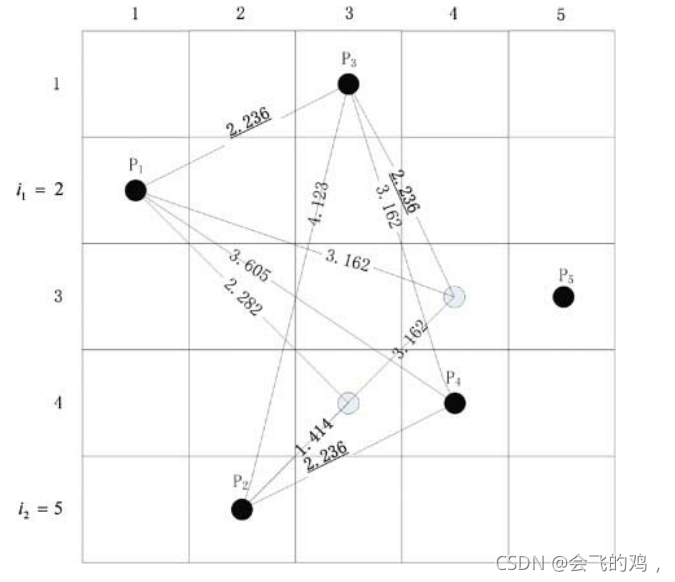
如上图所示,打算在二维空间采集5个点,根据拉丁超立方思想,样本点在每一维上每个区间内保证只有一个投影点,因此,在x,y轴上均分5个区间。首先从第一个点开始,为了方便,假设第i个样本点在x轴上的位置是第i个区间,第一个点p1在x轴上第一个区间,在y轴上的区间位置随机(图片上是编号为2的位置),根据投影区间只有一个样本点思想,那么第二个点p2在y轴上的位置就需要排除编号为2的位置,那么对于p2来说y轴上只有编号为1,3,4,5的位置可选,分别计算y轴位置在1,3,4,5的p2点与p1点距离,选择距离最大的那个y轴位置也就是编号为5的位置当做第二个样本点的最终位置。对于p3由于前两个样本点使用掉了2,5位置,因此p3样本点y轴位置只能在1,3,4选择,假如p3样本点在y轴位置是1,分别计算它与前面p1,p2样本点的距离,由图可知距离分别为2.236和4.123,那么它的特征距离也就是这两个距离最小值2.236,再分别用同样的方式,计算p3样本点y轴上的位置在3,4上的特征距离,选出特征距离最大的那个y轴位置就是最终p3样本点在y轴上的位置也就是图中所示的位置。依此类推计算出其他几个样本点的位置。这样就能够得到一个空间填充性能较好的样本点同时也满足拉丁超立方的投影特性。
matlab代码实现利用该方法在一个二维空间内采集十个样本点
X=zeros(10,2); %初始化采样点
X(1,:)=[1,ceil(10*rand(1))]; %第一个点横坐标为1,纵坐标1到10随机
A=[X(1,2)]; %用来存储存在的点所占用在纵坐标的标数
B=[1,2,3,4,5,6,7,8,9,10];
for i=2:10
isA=ismember(B,A);
C=B(~isA); %记录在该横坐标处剩余可用纵坐标的可用标号
[~,n]=size(C);
X(i,1)=i;
for j=1:n %从可用标号依次计算
X(i,2)=C(j);
for k=1:i-1
d(k)=sum((X(i,:)-X(k,:)).^2); %计算改点出与之前的点的距离的平方
end
distance(j)=min(d); %最小的距离就是该点处的特征距离
end
[~,index]=max(distance); %找到特征距离最大处的索引
X(i,2)=C(index); %最小距离最大的地方就是该点的纵坐标
A=[A,C(index)]; %加入占用纵坐标
clear distance %清除上一次迭代的变量
clear c
clear d
end
X(:,1)=X(:,1)/10-rand(10,1)/10;
X(:,2)=X(:,2)/10-rand(10,1)/10;
scatter(X(:,1),X(:,2),'filled')
grid on
xticks(0:0.1:1)
yticks(0:0.1:1)结果如下:
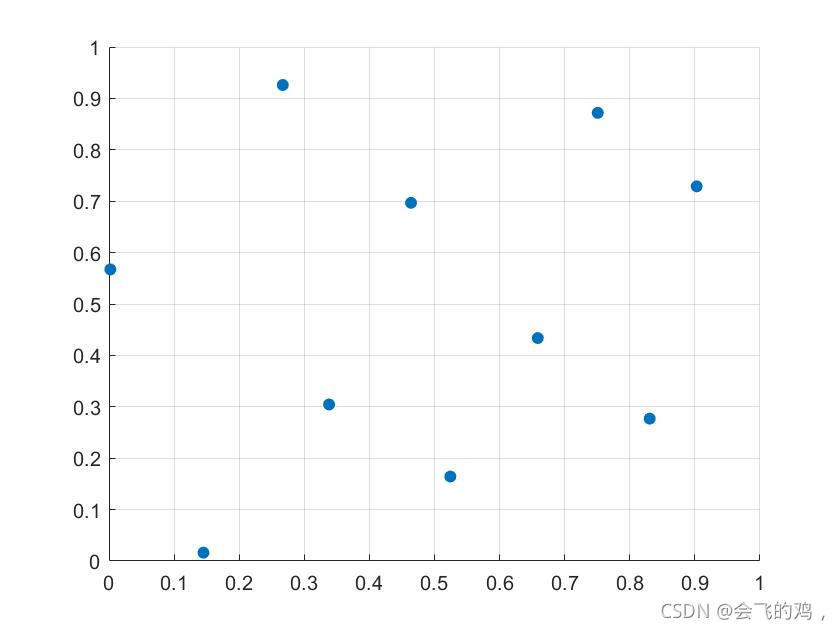
普通的拉丁超立方采样结果:?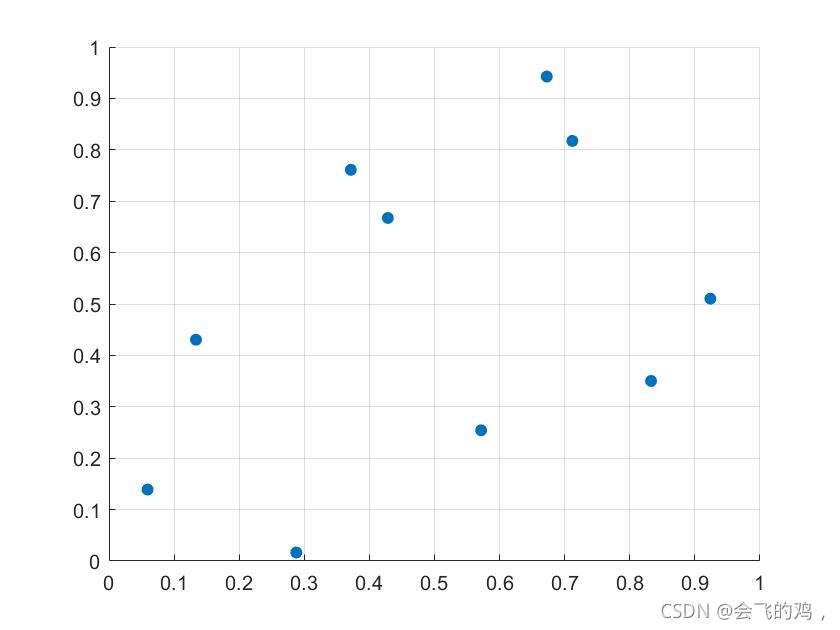
?可以看到样本点之间的距离相比于普通的拉丁超立方要更加离散,样本点不会发生聚集。空间分布更加均匀合理。
参考文献:
YI ?J,LI ?X,XIAO ?M,et ?al. ?Construction ?of ?nested maximin designs based on successive local enumeration and modified novel global harmony search algorithm[J]. Engineering Optimization,2017,49(1):161-180.